Random RPG damage distribution
- Transfer

For role-playing games such as Dungeons & Dragons, damage rolls are used to calculate attack damage . This is logical for a game whose process is based on dice rolls. In many computer RPGs, damage and other attributes (strength, magic points, dexterity, etc.) are calculated using a similar system.
Usually
random(), the call code is written first , and then the results are adjusted and adjusted to the desired behavior of the game. This article will cover three topics:- Simple adjustments - mean and variance
- Add asymmetry - discard results or add critical hits
- Complete freedom in setting random numbers, unlimited possibilities of cubes
The basics
This article assumes that you have a function that returns a random integer ranging from to . In Python you can use . Javascript can be used . There is C in the standard library , but it does not work well, so use a different random number generator. In C ++, you can connect to a random number generator object . In Java, you can create a random number generator object using , and then call for it . The standard libraries of many languages do not have good random number generators, but there are many third-party libraries, for example, PCG for C and C ++.
random(N)0range-1random.randrange(N)Math.floor(N * Math.random())rand() % Nuniform_int_distribution(0,N-1)new Random().nextInt(N)Let's start with one die. This bar graph shows the results of throws a 12-sided dice:
1+random(12). Since it random(12)returns a number from 0 to 11, and we need a number from 1 to 12, we add 1 to it. Damage is located on the X axis, and the frequency of receiving the corresponding damage is on the Y axis. For one dice, a damage roll of 2 or 12 is just as likely as a roll of 7. 
For throwing several dice, it is useful to use the entry used in dice games: N d S means that you need to roll the S- sided bone N times. A roll of one 12-sided bone is written as sided 1d12; 3d4 means you need to roll 4-sided dice three times. In code, this can be written as
3 + random(4) + random(4) + random(4).Let's roll two 6-sided dice (2d6) and summarize the results:
damage = 0
for each 0 ≤ i < 2:
damage += 1+random(6)Results can range from 2 (1 fell on both bones) to 12 (6 fell on both bones). The probability of getting 7 is higher than 12.

What happens if we increase the number of bones, but reduce their size?

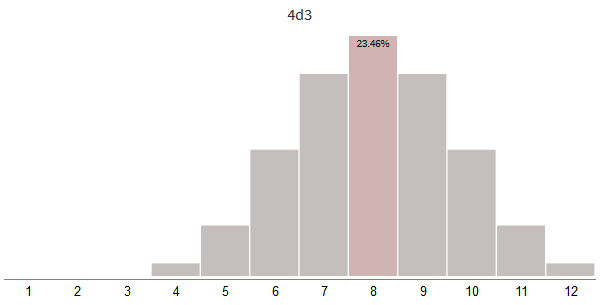

The most important effect is that the distribution will not be wide , but narrow . There is a second effect - the peak shifts to the right. Let's start by exploring the use of offsets.
Constant offsets
Part of the weapon in Dungeons & Dragons gives bonus damage. You can record 2d6 + 1 to indicate a bonus of +1 to damage. In some games, armor or shields reduce damage. You can write 2d6-3, which means removing 3 points of damage (in this example, I will assume that the minimum damage is 0).
Let's try to shift the damage to the negative (to reduce damage) or to the positive (for damage bonus) sides:
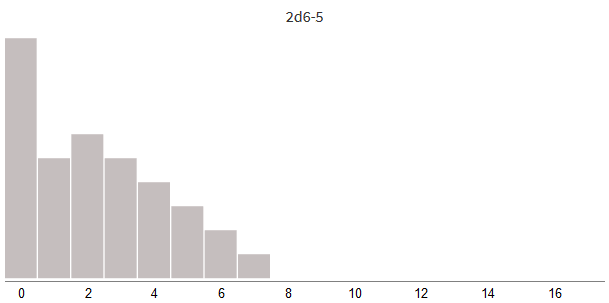



By adding a damage bonus or subtracting the blocked damage, we simply shift the entire distribution to the left or right.
Distribution dispersion
When passing from 2d6 to 6d2, the distribution becomes narrower and shifts to the right. As we saw in the previous section, displacement is a simple shift. Let's look at the variance of the distribution.
We define a function for N throws in a row that returns a number from 0 to N * S :
random(S+1)function rollDice(N, S):
# Сумма N костей, каждая из которых имеет значение от 0 до S
value = 0
for 0 ≤ i < N:
value += random(S+1)
return valueGenerating random numbers from 0 to 24 using several bones gives the following distribution of results:
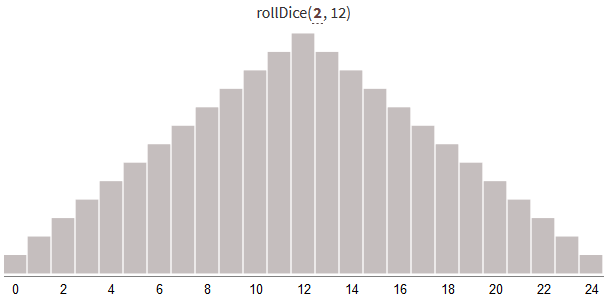



With an increase in the number of throws and maintaining a constant range from 0 to N * S, the distribution becomes narrower (with less dispersion). More results will be near the middle of the range.
Note: as the number of S sides increases (see images below) and dividing the result by S, the distribution approaches normal . A simple way to randomly select from a normal distribution is the Box-Muller transform .
Asymmetry
The distributions for are symmetric . Values below the average are as likely as values above the average. Is this suitable for your game? If not, then there are different techniques for creating asymmetry.
rollDice(N, S)Shot clipping or throwing
Suppose we want more than average values to be more frequent than less than average. Such a scheme is rarely used for damage, but is applicable for attributes such as strength, intelligence, etc. One of the ways to implement it is to make several throws and choose the best result.
Let's try to roll the dice
rollDice(2,20)twice and choose the maximum result:roll1 = rollDice(2, 20)
roll2 = rollDice(2, 20)
damage = max(roll1, roll2)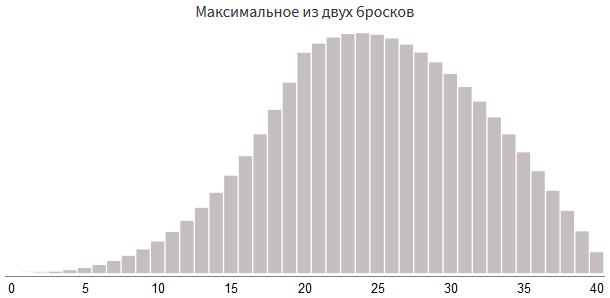
When choosing the maximum of
rollDice(2, 12)and rollDice(2, 12)we get a number from 0 to 24. Another way to get a number from 0 to 24 is to use it rollDice(1, 12)three times and choose the best two of the three results. The shape will be even more asymmetric than when choosing one of two rollDice(2, 12):roll1 = rollDice(1, 12)
roll2 = rollDice(1, 12)
roll3 = rollDice(1, 12)
damage = roll1 + roll2 + roll3
# теперь отбрасываем наименьшее:
damage = damage - min(roll1, roll2, roll3)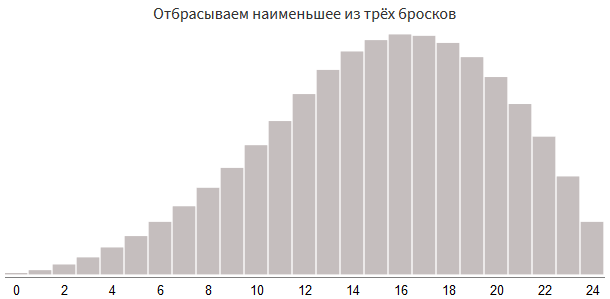
Another way is to throw the smallest result. In general, it is similar to the previous approaches, but differs slightly in implementation:
roll1 = rollDice(1, 8)
roll2 = rollDice(1, 8)
roll3 = rollDice(1, 8)
damage = roll1 + roll2 + roll3
# теперь отбрасываем наименьшее и бросаем снова:
damage = damage - min(roll1, roll2, roll3)
+ rollDice(1, 8)
Any of these approaches can be used for reverse asymmetry, making the values less frequent than average more frequent. We can also assume that the distribution creates random bursts of high values. This distribution is often used for damage and rarely for attributes. Here
max()we change to min():roll1 = rollDice(2, 12)
roll2 = rollDice(2, 12)
damage = min(roll1, roll2)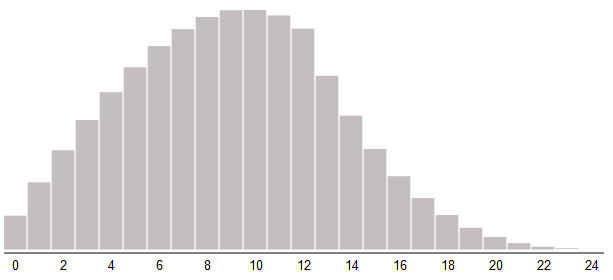
We discard the largest of the two throws
Critical hits
Another way to create random bursts of high damage is to implement them more directly. In some games, a certain bonus gives a “critical hit”. The simplest bonus is additional damage. In the code below, critical damage is added in 5% of cases:
damage = rollDice(3, 4)
if random(100) < 5:
damage += rollDice(3, 4)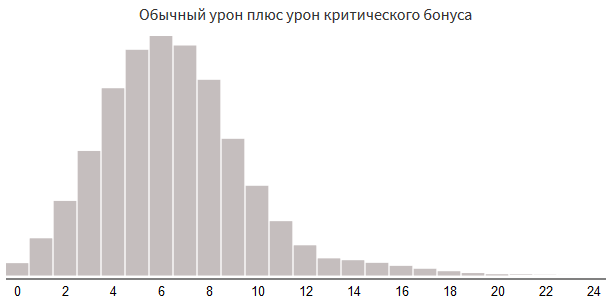
Critical strike probability 5%
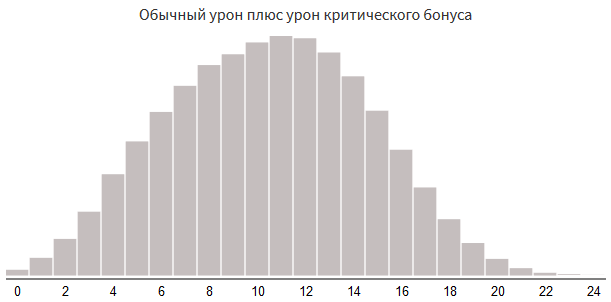
Critical strike probability 60%
In other approaches to adding asymmetry, additional attacks are used: with critical hits there is a chance of additional critical hits being triggered; when critical hits, a second attack is triggered, breaking through the defense; during critical hits, the enemy misses during the attack. But in this article I will not consider the distribution of damage in multiple attacks.
Let's try to create our own distribution
When using randomness (damage, attributes, etc.), we need to start with a description of the distribution characteristics that we need for the game process:
- Interval: what will be the minimum and maximum values (if any)? Use scaling and offset to fit the distribution in this interval.
- Dispersion: how often should values be close to average? Fewer throws may be used for greater dispersion, or more for lesser dispersion.
- Asymmetry: Do you need more or less average values? Use min, max or critical bonuses to add asymmetry to the distribution.
Here are a couple of examples with some of the options:
value = 0 + rollDice(3, 8)
# Min с перебрасыванием:
value = min(value, 0 + rollDice(3, 8))
# Max с перебрасыванием:
value = max(value, 0 + rollDice(3, 8))
# Критический бонус:
if random(100) < 15:
value += 0 + rollDice(7, 4)value = 0 + rollDice(3, 8)
# Min с перебрасыванием:
value = min(value, 0 + rollDice(3, 8))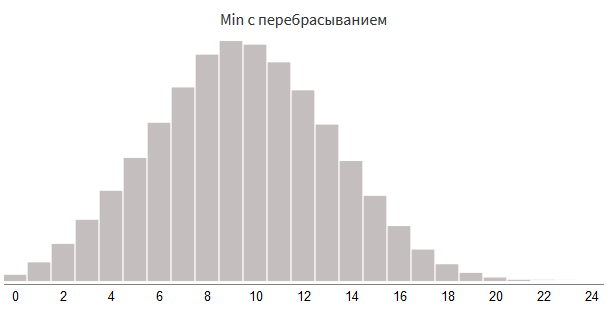
value = 0 + rollDice(3, 8)
# Max с перебрасыванием:
value = max(value, 0 + rollDice(3, 8))
# Критический бонус:
if random(100) < 15:
value += 0 + rollDice(7, 4)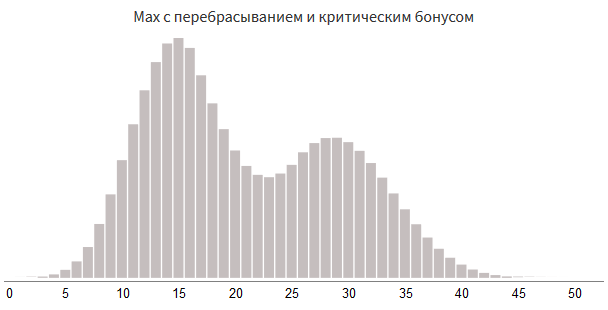
There are many other ways to structure random numbers, but I hope these examples give an idea of how flexible the system is. It is also worth looking at this damage roll calculator . However, sometimes dice combinations are not enough.
Free Forms
We started with input algorithms and studying the corresponding output distributions. We had to sort through a lot of input algorithms to find the result we needed. Is there a more direct way to get a suitable algorithm? Yes!
Let's do the opposite and start with the output we need, presented as a histogram. Let's try to do this with a simple example.
Suppose I need to choose from 3, 4, 5 and 6 in the following proportions:
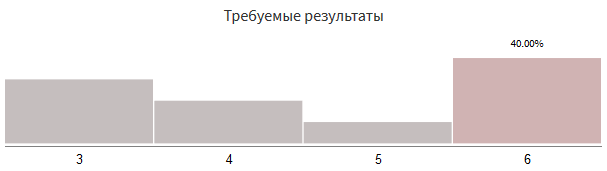
This does not correspond to anything that can be obtained by throwing bones.
How to write code for these results?
x = random(30+20+10+40)
if x < 30: value = 3
else if x < 30+20: value = 4
else if x < 30+20+10: value = 5
else: value = 6Examine this code and see how it works before moving on to the next steps. Let's make the code more general so that it can be used for different probability tables. The first step is to create a table:
damage_table = [ # массив (вес, урон)
(30, 3),
(20, 4),
(10, 5),
(40, 6),
];In this hand-written code, each construct
ifcompares xwith a total sum of probabilities. Instead of writing separate constructions ifwith manually specified sums, we can cycle through all the entries in the table:cumulative_weight = 0
for (weight, result) in table:
cumulative_weight += weight
if x < cumulative_weight:
value = result
breakThe last thing to generalize is the sum of the table entries. Let's calculate the sum and use it to select a random x:
sum_of_weights = 0
for (weight, value) in table:
sum_of_weights += weight
x = random(sum_of_weights)Combining everything together, we can write a function to search for results in the table and a function to select a random result (you can turn them into methods of the damage table class):
function lookup_value(table, x):
# считаем, что 0 ≤ x < sum_of_weights
cumulative_weight = 0
for (weight, value) in table:
cumulative_weight += weight
if x < cumulative_weight:
return value
function roll(table):
sum_of_weights = 0
for (weight, value) in table:
sum_of_weights += weight
x = random(sum_of_weights)
return lookup_value(damage_table, x)The code for generating numbers from a table is very simple. For my tasks, it was fast enough, but if the profiler reports that it is too slow, try speeding up the linear search with binary / interpolation searches, lookup tables, or the alias method . See also the inverse transform method .
Draw your own distribution
This method is convenient in that it allows you to use any form.
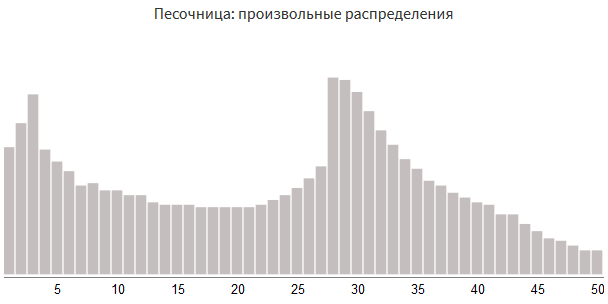
damage_table = [(53,1), (63,2), (75,3), (52,4), (47,5), (43,6), (37,7), (38,8), (35,9), (35,10), (33,11), (33,12), (30,13), (29,14), (29,15), (29,16), (28,17), (28,18), (28,19), (28,20), (28,21), (29,22), (31,23), (33,24), (36,25), (40,26), (45,27), (82,28), (81,29), (76,30), (68,31), (60,32), (54,33), (48,34), (44,35), (39,36), (37,37), (34,38), (32,39), (30,40), (29,41), (25,42), (25,43), (21,44), (18,45), (15,46), (14,47), (12,48), (10,49), (10,50)]With this approach, we can choose a distribution that matches any gameplay, not limited to the distributions created by the rolls of dice.
Conclusion
Random damage throws and random attributes are implemented simply. You, as a game designer, must choose the properties that the final distribution will have. If you will use dice rolls:
- Use the number of throws to control dispersion . A small amount corresponds to a high dispersion, and vice versa.
- Для управления масштабом используйте смещение и размер кости. Если вы хотите, чтобы случайные числа находились в интервале от X до Y, то при каждом из N бросков должно получаться случайное число от 0 до (Y-X)/N, после чего к нему прибавляется X. Положительные смещения можно использовать для бонусов урона или бонусов атрибутов. Отрицательные смещения можно использовать для блокировки урона.
- Для более частых значений больше или меньше среднего используйте асимметрию. Для бросков атрибутов чаще требуются значения выше среднего, их можно получить выбором максимального, лучшего из трёх или перебрасыванием минимального значения. Для бросков урона чаще требуются значения ниже среднего, их можно получить выбором минимального или критическими бонусами. Для сложности случайных встреч с врагами тоже часто используются значения ниже среднего.
Think about how distribution should vary in your game. Attack bonuses, damage blocking and critical hits can be used to vary the distribution with simple parameters. These parameters can be associated with items in the game. Use the sandbox in the original article to observe how these parameters affect distributions. Think about how distribution should work when the player’s level rises; see on this page for information on increasing and decreasing dispersion over time when calculating distributions using AnyDice (which is a great blog about ).
Unlike board game players with dice, you are not limited to distributions based on sums of random numbers. Using the code written in the section “Let's try to create our own distribution”, you can use any distribution . You can write a visual tool that allows you to draw histograms, save data to tables, and then draw random numbers based on this distribution. You can modify tables in JSON or XML format. You can also edit tables in Excel and export them to CSV. Parameter-free distributions provide greater flexibility, and using data tables instead of code allows fast iterations without recompiling the code.
There are many ways to implement interesting probability distributions based on simple code. First, decide on the properties that you need, and then select the code for them.
