August 10, 2017 at 08:51

Math detective: finding positive integer solutions to the equation

Original author: Alon Amit
  • Transfer
“I experimented with cubic representation tasks in the style of the previous work by Andrew and Richard Guy. The numerical results were amazing ... "( Comment on MathOverflow)
This is how the retired mathematician Allan MacLeod stumbled upon this equation several years ago. And it is really very interesting. Honestly, this is one of the best Diophantine equations that I have ever seen, but I have not seen very many of them.

I found it when it began to spread as a pseudo-picture that snatches on the net of nerds, invented by someone's ruthless mind ( Sridhar , was that you?). I did not immediately understand what it is. The picture looked like this:


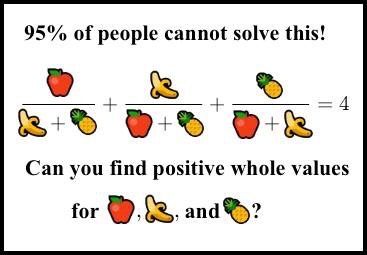
“95% of people will not solve this riddle. Can you find positive integer values? ”

You've probably already seen similar meme pictures. This is always pure rubbish, click bates: "95% of MIT graduates will not solve it!" “She” is some kind of stupid or poorly formulated task, or a trivial workout for the brain.

But this picture is completely different . This meme is a smart or evil joke. Approximately 99.999995% of people do not have the slightest chance of solving it, including a good portion of mathematicians from leading universities who are not involved in number theory. Yes, it is solvable, but it’s really complicated. (By the way, Sridhar did not come up with it, or rather, he did not completely. See the story in this comment ).

You might think that if nothing else helps, then you can just make the computer solve it. It is very simple to write a computer program to find solutions to this seemingly simple equation. Of course, the computer will sooner or later find them, if they exist. Big mistake . Here, a simple computer brute force method will be useless.

I don’t know whether it will be possible to fit the complete solution into the article, if not to accept that everyone already knows everything necessary about elliptic curves. I can only give a brief overview here. The main reference source is a wonderful, relatively recent work by Bremner and MacLeod entitled An unusual cubic representation problem , published in 2014 inAnnales Mathematicae et Informaticae .

So let's get started.


We are looking for positive integer solutions to the equation

$ \ frac {a} {b + c} + \ frac {b} {a + c} + \ frac {c} {a + b} = 4 \ tag 1 $


(I replaced the designations of variables with those used in the work).

The first thing to do when examining any equation is to try to put it in the right context. One must ask the question: what is this equation? So, we are asked to find integer solutions, that is, it is a number theory problem. In the current formulation, rational functions are used in the equation (polynomials divisible by other polynomials), but it is obvious that we can multiply by the common multiple of denominators to clean up the equation and get only polynomials, that is, bring it to the form of a Diophantine equation . The requirement of “positivity” is rather unusual, and, as we shall see, complicates everything.

So how many variables do we have here? The question seems silly: obviously, three, namely$ a $, $ b $ and $ c $. But take your time. An experienced number theory researcher will instantly notice that the equation is homogeneous . This means that if$ (a, b, c) $ is one of the solutions of the equation, then the solution is and $ (7a, 7b, 7c) $. Do you understand why? Multiplying each variable by some constant ($ 7 $ - this is just an example), we will not change anything, because the constant in each of the parts is reduced.

$ \ frac {ta} {tb + tc} = \ frac {ta} {t (b + c)} = \ frac {a} {b + c} $


This means that the equation only pretends to be three-dimensional. In fact, it is two-dimensional. In the geometric representation, we have a surface (one equation with three variables generally defines a two-dimensional surface. In general,$ k $ equations with $ n $ set variables $ d $-dimensional manifold, where $ d = nk $) But this surface is actually limited by a line that oscillates and passes through the origin. The resulting surface can be understood by understanding how it cuts through a unit plane. This is a projective curve.

The simplest way to comprehend this information is as follows: we can divide the decisions, whatever they may be, into those for which$ c = 0 $, and those for which $ c \ neq 0 $. In the first case, we have only two variables left,$ a $ and $ b $, and in the second we can simply divide by $ c $ and get a solution when $ c = 1 $. Therefore, we can simply look for rational solutions in$ a $ and $ b $ for case $ c = 1 $, multiply them by a common factor and get an integer solution in$ a $, $ b $ and $ c $. In essence, integer solutions of homogeneous equations correspond to rational solutions of an inhomogeneous version, which is one dimension less.

Continuing: what is the degree of our equation? The degree of an equation is the maximum degree of any that appears in the equation of a monomial, where the “monomial” is the product of several variables whose “degree” is the number of multiplied monomials. For instance,$ a ^ 2bc ^ 4 $ will be a monomial of degree $ 7 = 2 + 1 + 4 $.

The behavior of Diophantine equations strongly depends on their degree. Generally:

  • With degree $ 1 $ everything is simple.
  • Power $ 2 $ fully analyzed and can be solved in fairly elementary ways.
  • Power $ 3 $ - This is a vast ocean of deep theory and a million unsolved problems.
  • Power $ 4 $ and higher ... Very, very complex.

We have a degree $ 3 $. Why? We simply multiply by dividers:

$ a (a + b) (a + c) + b (b + a) (b + c) + c (c + a) (c + b) = 4 (a + b) (a + c) (b + c) $


Even without opening the brackets, you can see that the degree is $ 3 $: we never multiply more than three variables at a time. We get parts like$ a ^ 3 $, $ b ^ 2c $ and $ abc $, but there will never be anything more than three factors. If we carry out the transformation, the equation will be

$ a ^ 3 + b ^ 3 + c ^ 3-3 (a ^ 2b + ab ^ 2 + a ^ 2c + ac ^ 2 + b ^ 2c + bc ^ 2) -5abc = 0 $


You may argue that multiplication by divisors is not possible if some of them are equal $ 0 $. This is true - indeed, our new equation has several solutions that do not correspond to the original equation. But actually it’s good. The version with polynomials adds several “patches” to the original and it becomes easier to work with it. We just need to check if the original divisors do not disappear with each concrete decision.

In fact, an equation with polynomials is easy to solve, for example,$ a = -1 $, $ b = 1 $, $ c = 0 $. This is good: we have a rational solution (rational point). This means that our cubic equation (degree = 3) is actually an elliptic curve .

When you find that the equation is an elliptic curve, then a) you are happy and b) you despair, because there is still much to learn. This equation is a great example of how a powerful theory of elliptic curves can be applied to finding insanely complex solutions.


The first thing that an elliptic curve is usually made is to bring it into Weierstrass form. This is an equation that looks like

$ y ^ 2 = x ^ 3 + ax + b $


and sometimes how

$ y ^ 2 = x ^ 3 + ax ^ 2 + bx + c $


(This is called an expanded Weierstrass form. It is optional, but sometimes more convenient).

Usually, any elliptic curve can be reduced to this form (unless you are working on fields with small characteristics, but here we do not need to worry about them). It would be too long to explain the way to find the right transformation, so just know that this is an absolutely mechanical process (it is critical that there is at least one rational point that we have). There are different packages of computational algebra that will do everything for you.

But even if you do not know. how to find the transformation, it is very simple to check, at least it is done purely mechanically. The necessary transformation in our case is given by scary-looking formulas

$ x = \ frac {-28 (a + b + 2c)} {6a + 6b-c} $


$ y = \ frac {364 (ab)} {6a + 6b-c} $


I know that they look like the voodoo magic that came from nowhere, but believe me, this is not so. Having obtained these transformations, using monotone, but rather simple algebraic calculations, we show that

$ y ^ 2 = x ^ 3 + 109x ^ 2 + 224x \ tag 2 $


This equation, although it looks completely different, is in fact a reliable model of the original. Graphically, it looks like this - a typical elliptical curve with two real parts: the



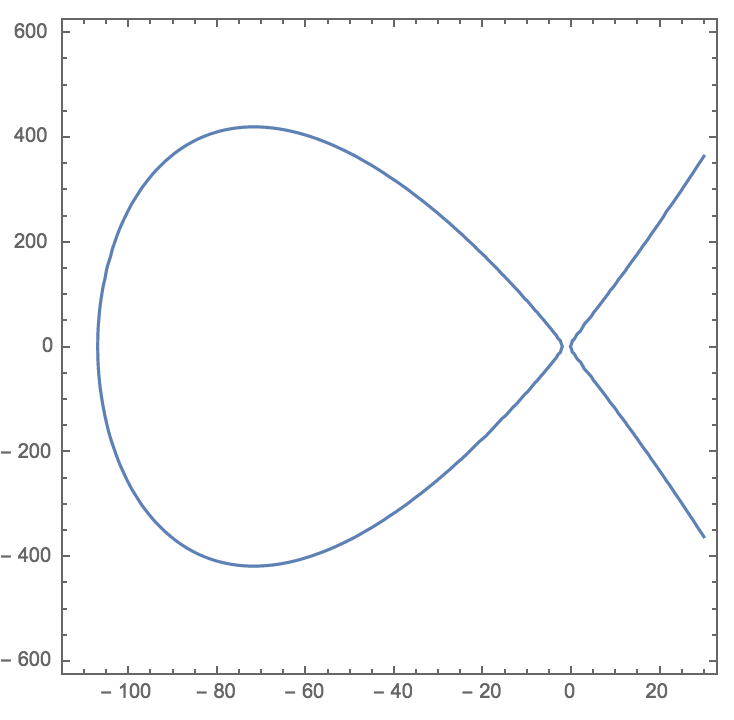
"Fish tail" on the right grows "to infinity and beyond." The oval shape on the left is closed and is quite interesting for us.

Having any solution$ (x, y) $ of this equation, we can restore the necessary values $ a $, $ b $, $ c $ using equations

$ a = \ frac {56-x + y} {56-14x} $


$ b = \ frac {56-xy} {56-14x} $


$ c = \ frac {-28-6x} {28-7x} $


(Remember that triplet $ (a: b: c) $you need to take it projectively - whatever values ​​you get using these equations, you can always multiply them by any constant).

The two displays shown by us, from$ a $, $ b $, $ c $ in $ x $, $ y $and vice versa, they show that these two equations are “the same” in terms of number theory: rational solutions of one give rational solutions of the other. Technically, this is called birational equivalence , and it is a fundamental concept of algebraic geometry. As we have already noticed, there may be exception points that are not displayed correctly. These are cases when$ a + b $, $ a + c $ or $ b + c $ are equal $ 0 $. This is the usual retribution in the case of birational equivalence, and it should not cause any unrest.


Let's look at an example.

There is a good rational point on the elliptic curve (2):

$ x = -100 $, $ y = 260 $. Perhaps it is not so easy to find, but it is very simple to check : just insert these values ​​and you will see that the two halves are the same (I did not select this point randomly, but so far it does not matter). You can simply check which values$ a $, $ b $, $ c $she gives us. We get$ a = 2/7 $, $ b = -1 / 14 $, $ c = 11/14 $, and since we can multiply by the common factor, the results are converted to $ a = 4 $, $ b = -1 $, $ c = 11 $.

And indeed

$ \ frac {4} {- 1 + 11} + \ frac {-1} {4 + 11} + \ frac {11} {4-1} = 4 $


as you can easily see. This is a simple solution to our original equation in integers, but, alas, not in positive integers. This solution is not easy to derive manually, but it is also easy to obtain without all of the crypts considered here, with a little patience. The most difficult thing is positive solutions.

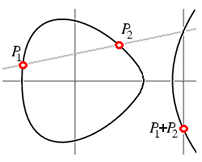
Now, having received a rational point on an elliptic curve, for example,$ P = (- 100,260) $on our curve (2), you can start generating others using the chord and tangent technique discussed in a previous article on Quora.



First, add our point$ P $ to herself, finding the tangent to the curve at the point $ P $and determining where she meets the curve again. The result will be a little scary:

$ P + P = 2P = (8836/25, -950716/125) $


and again this new point corresponds to the values $ a $, $ b $, $ c $being a solution to the original equation

$ (a, b, c) = (9499, -8784, 5165) $


This solution is definitely not easy to find manually, but it is still within the power of the computer. However, it is still not positive.

Without fear of failure, we continue to calculate$ 3P = 2P + P $that can be determined by connecting a straight line $ P $ and $ 2P $and finding the third intersection point with the curve. And again we calculate$ a $, $ b $, $ c $, and again the result is not positive. The same thing will happen with$ 4P $, and with $ 5p $and so on ... until we stumble upon $ 9p $. It is definitely not easy to find, but with the help of our machinery we only need to repeat a simple geometric procedure nine times. Matching Values

9P=(-66202368404229585264842409883878874707453676645038225/13514400292716288512070907945002943352692578000406921,
58800835157308083307376751727347181330085672850296730351871748713307988700611210/1571068668597978434556364707291896268838086945430031322196754390420280407346469)

$ a $, $ b $, $ c $awesome: These are 80-bit numbers! You could never have found 80-bit numbers on a computer with a simple brute force. It looks incredible, but pasting these huge numbers into a simple expression

a=154476802108746166441951315019919837485664325669565431700026634898253202035277999,
b=36875131794129999827197811565225474825492979968971970996283137471637224634055579,
c=4373612677928697257861252602371390152816537558161613618621437993378423467772036

$ a / (b + c) + b / (a ​​+ c) + c / (a ​​+ b) $we really get exactly $ 4 $.

In fact, they are the smallest solutions to the problem. If we continue to add a point to ourselves$ P $, then the dividers will simply grow. It is not easy to prove this, because there is always a possibility of reduction, but the height theory for the elliptic curve allows us to show that these astronomical numbers are actually the simplest solution to the equation.




Back to the theory. An elliptic curve over rational values ​​has a rank , which is the number of points needed to use for the chords and tangents method and to be sure that sooner or later we will find all rational points on the curve. Our elliptic curve (2) has rank 1. This means that it has an infinite number of rational points, but they all come from the only one, which is nothing other than our point$ P = (- 100, 260) $. The algorithms for calculating the rank and finding such a generator are far from trivial, but SageMath (now called CoCalc) performs them in less than a second in just a few lines of code. My code can be found here . It reproduces the whole solution from scratch, but, of course, uses the built-in Sage methods to work with elliptic curves.

In our case, the point$ P $ lies on the oval part of the curve, like points $ mP $ for any positive integer $ m $. They “circle” along the oval and are gradually fairly evenly distributed over it. This is very successful, because only a small part of this oval gives positive decisions regarding$ a $, $ b $, $ c $: This is the bold portion of the graph below, taken from Bremner and MacLeod.



Points$ P $, $ 2P $, and so on, do not lie on the selected part, but $ 9p $- lies, that's exactly how we got our 80-bit positive solutions.

Bremner and MacLeod studied what happens if we replace$ 4 $something else. If you think that the solutions will be large, then wait until you see what the solutions will be as a result$ 178 $. Instead of 80 bits, we need 398,605,460 bits. Yes, this is only the number of digits of the solution. If you replace the result with$ 896 $, then the solution will contain trillions of bits. Trillions. For this innocent looking equation:

$ a / (b + c) + b / (a ​​+ c) + c / (a ​​+ b) = 896 $



A striking example of how Diophantine equations with small coefficients can have huge solutions. This inspires not just awe, but a feeling of bottomlessness. A negative solution to the tenth Hilbert problem means that the growth of solutions with increasing coefficients is a non-computable function , because if it were computable, then we would have a simple algorithm for solving Diophantine equations, and it does not exist (neither simple nor complex). Conformity$ 4 \ to $ 80-bit numbers $ 178 \ to $ numbers of hundreds of millions of digits and $ 896 \ to $trillions of bits gives us a little idea of ​​the first, small steps of this monstrous uncalculated function. Change the numbers in the equation a little, and the decisions will easily surpass everything that can fit into our miserable, tiny Universe.

Here's a surprisingly tricky little equation.

Thanks to MrShoor for sending me a link to this interesting article.
Tags:

Also popular now: