June 26, 2017 at 13:25

Keras Auto Encoders, Part 4: Conditional VAE

  • Tutorial

Content



In the last part, we met with variational auto-encoders (VAE) , implemented this on keras , and also understood how to generate images using it. The resulting model, however, had some drawbacks:

  1. Not all of the numbers turned out to be well-coded in hidden space: some of the numbers were either absent or very blurry. In the gaps between the regions in which variants of the same figure were concentrated, there were generally some meaningless hieroglyphs.

    What can I write, this is how the generated numbers looked like:

    Picture


  2. It was difficult to generate a picture of some given digit. To do this, it was necessary to look into what area of ​​the latent space the images of a specific figure fell, and to sample from somewhere else, and even more difficult to generate a figure in some given style.

In this part, we will look at how we can only slightly complicate the model to overcome both of these problems, and at the same time get the opportunity to generate pictures of new digits in the style of another digit - this is probably the most interesting feature of the future model.



First, let's think about the reasons for the 1st drawback:


The manifolds on which various numbers lie can be far from each other in the space of pictures. That is, it is difficult to imagine how, for example, to continuously display the picture of the number “5”, in the picture of the number “7”, while all the intermediate pictures could be called plausible. Thus, the variety around which the numbers lie does not have to be linearly connected at all. The auto encoder, due to the fact that it is a composition of continuous functions, can itself be displayed in the code and vice versa only continuously, especially if it is a variational auto encoder. In our previous example, everything was complicated by the fact that the auto-encoder tried to search for a two-dimensional manifold.

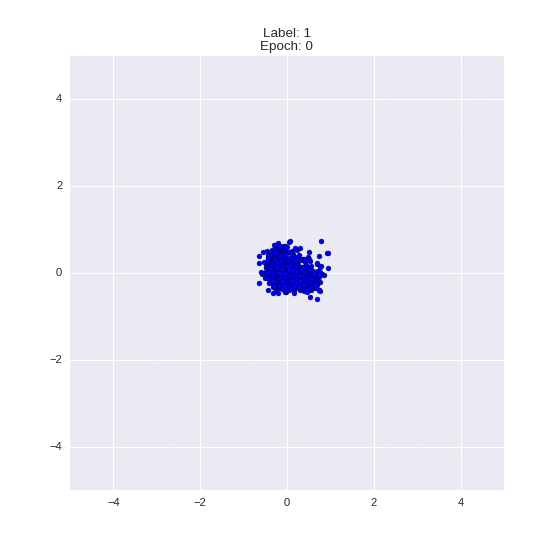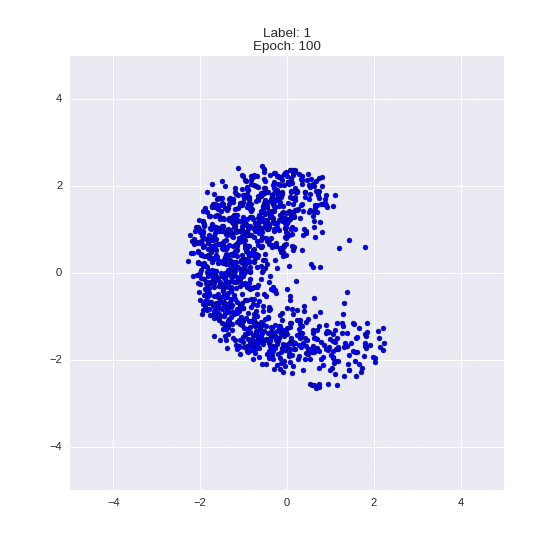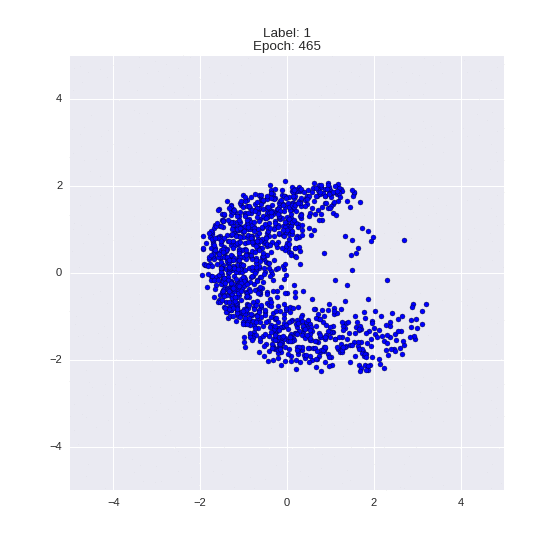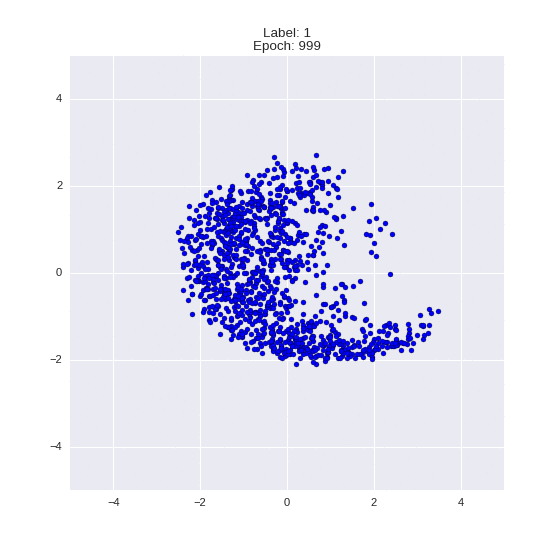
As an illustration, let us return to our artificial example from the second part, we only make the defining variety incoherent:


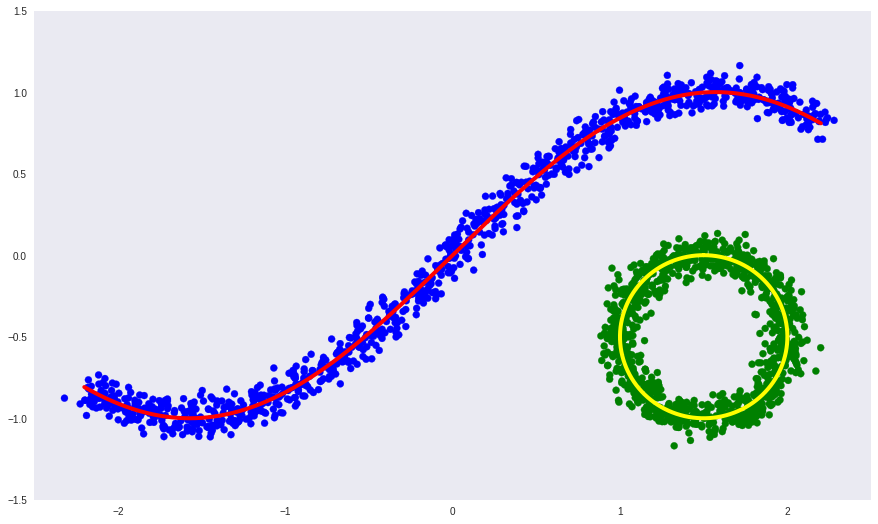
Here:

  • blue and green dots - objects of selection,
  • the red and yellow curves are an unrelated defining variety.

Now let’s try to learn the defining variety using the usual deep auto-encoder.

The code
# Импорт необходимых библиотек
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
# Создание датасета
x1 = np.linspace(-2.2, 2.2, 1000)
fx = np.sin(x1)
dots1 = np.vstack([x1, fx]).T
t = np.linspace(0, 2*np.pi, num=1000)
dots2 = 0.5*np.array([np.sin(t), np.cos(t)]).T + np.array([1.5, -0.5])[None, :]
dots = np.vstack([dots1, dots2])
noise = 0.06 * np.random.randn(*dots.shape)
labels = np.array([0]*1000 + [1]*1000)
noised = dots + noise
# Визуализация
colors = ['b']*1000 + ['g']*1000
plt.figure(figsize=(15, 9))
plt.xlim([-2.5, 2.5])
plt.ylim([-1.5, 1.5])
plt.scatter(noised[:, 0], noised[:, 1], c=colors)
plt.plot(dots1[:, 0], dots1[:, 1],  color="red",    linewidth=4)
plt.plot(dots2[:, 0], dots2[:, 1],  color="yellow", linewidth=4)
plt.grid(False)
# Модель и обучение
from keras.layers import Input, Dense
from keras.models import Model
from keras.optimizers import Adam
def deep_ae():
    input_dots = Input((2,))
    x = Dense(64, activation='elu')(input_dots)
    x = Dense(64, activation='elu')(x)
    code = Dense(1, activation='linear')(x)
    x = Dense(64, activation='elu')(code)
    x = Dense(64, activation='elu')(x)
    out = Dense(2, activation='linear')(x)
    ae = Model(input_dots, out)
    return ae
dae = deep_ae()
dae.compile(Adam(0.001), 'mse')
dae.fit(noised, noised, epochs=300, batch_size=30, verbose=2)
# Результат
predicted = dae.predict(noised)
# Визуализация
plt.figure(figsize=(15, 9))
plt.xlim([-2.5, 2.5])
plt.ylim([-1.5, 1.5])
plt.scatter(noised[:, 0], noised[:, 1], c=colors)
plt.plot(dots1[:, 0], dots1[:, 1],  color="red",    linewidth=4)
plt.plot(dots2[:, 0], dots2[:, 1],  color="yellow", linewidth=4)
plt.scatter(predicted[:, 0], predicted[:, 1], c='white', s=50)
plt.grid(False)



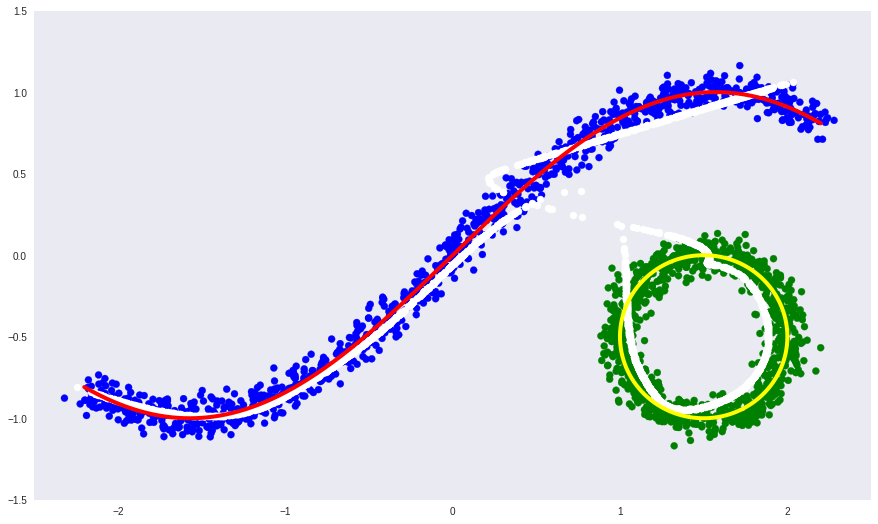
  • the white line is the variety into which the blue and green data points pass after the auto-encoder, that is, the attempt of the auto-encoder to build a manifold that defines the most variation in the data.

It can be seen that a simple auto-encoder could not learn the form of a disconnected manifold. Instead, he slyly continued one into the other.

If we know the data labels that determine which part of the disconnected manifold these data lie on (as with the numbers), then we can simply condition the auto-encoder on these labels. That is, simply additionally with the data to submit to the input of the encoder and decoder also data labels. In this case, the source of the discontinuity in the data will be the label, and this will allow the auto-encoder to learn each part of the linearly disconnected manifold separately.

Let's look at the same example, only now we will also transfer the label to the input to the encoder and decoder.

The code
from keras.layers import concatenate
def deep_cond_ae():
    input_dots = Input((2,))
    input_lbls = Input((1,))
    full_input = concatenate([input_dots, input_lbls])
    x = Dense(64, activation='elu')(full_input)
    x = Dense(64, activation='elu')(x)
    code = Dense(1, activation='linear')(x)
    full_code = concatenate([code, input_lbls])
    x = Dense(64, activation='elu')(full_code)
    x = Dense(64, activation='elu')(x)
    out = Dense(2, activation='linear')(x)
    ae = Model([input_dots, input_lbls], out)
    return ae
cdae = deep_cond_ae()
cdae.compile(Adam(0.001), 'mse')
cdae.fit([noised, labels], noised, epochs=300, batch_size=30, verbose=2)
predicted = cdae.predict([noised, labels])
# Визуализация
plt.figure(figsize=(15, 9))
plt.xlim([-2.5, 2.5])
plt.ylim([-1.5, 1.5])
plt.scatter(noised[:, 0], noised[:, 1], c=colors)
plt.plot(dots1[:, 0], dots1[:, 1],  color="red",    linewidth=4)
plt.plot(dots2[:, 0], dots2[:, 1],  color="yellow", linewidth=4)
plt.scatter(predicted[:, 0], predicted[:, 1], c='white', s=50)
plt.grid(False)



This time, the auto-encoder managed to learn a linearly disconnected defining manifold.

CVAE


If we now take VAE , as in the previous part, and submit labels as well, we get Conditional Variational Autoencoder (CVAE) .

With pictures of numbers it turns out like this: The



picture above from [2]

In this case, the main VAE equation from the last part becomes simply conditioned on Y( Ydoes not have to be discrete), that is, on the label.

\ log P (X | Y; \ theta_2) - KL [Q (Z | X, Y; \ theta_1) || P (Z | X, Y; \ theta_2)] = E_ {Z \ sim Q} [\ log P (X | Z, Y; \ theta_2)] - KL [Q (Z | X, Y; \ theta_1) || N (0, I)]

Q (Z | X, Y; \ theta_1)we compare again with N (0, I).
This can be interpreted as follows: for each Ywe have a separate VAE auto-encoder , while they have a huge amount of common weights (almost absolute weight sharing ).

As a result, it turns out that CVAE encodes in the Zproperties of the input signal common to all Y.

Style transfer


(Comment: this is not the same as transferring the style to Prisme, it’s completely different there)

Now it becomes clear how to create new images in the style given:

  1. we train CVAE in pictures with labels,
  2. we encode the style of the given picture in Z,
  3. changing labels Y, we create Znew pictures from the encoded one .

Code for Keras


The code is almost identical to the code from the previous part, except that now the digit label is also transmitted to the encoder and decoder.

The code
import sys
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# import seaborn as sns
from keras.datasets import mnist
from keras.utils import to_categorical
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.astype('float32') / 255.
x_test  = x_test .astype('float32') / 255.
x_train = np.reshape(x_train, (len(x_train), 28, 28, 1))
x_test  = np.reshape(x_test,  (len(x_test),  28, 28, 1))
y_train_cat = to_categorical(y_train).astype(np.float32)
y_test_cat  = to_categorical(y_test).astype(np.float32)
num_classes = y_test_cat.shape[1]


batch_size = 500
latent_dim = 8
dropout_rate = 0.3
start_lr = 0.001


from keras.layers import Input, Dense 
from keras.layers import BatchNormalization, Dropout, Flatten, Reshape, Lambda
from keras.layers import concatenate
from keras.models import Model
from keras.objectives import binary_crossentropy
from keras.layers.advanced_activations import LeakyReLU
from keras import backend as K
def create_cvae():
    models = {}
    # Добавим Dropout и BatchNormalization
    def apply_bn_and_dropout(x):
        return Dropout(dropout_rate)(BatchNormalization()(x))
    # Энкодер
    input_img = Input(shape=(28, 28, 1))
    flatten_img = Flatten()(input_img)
    input_lbl = Input(shape=(num_classes,), dtype='float32')
    x = concatenate([flatten_img, input_lbl])
    x = Dense(256, activation='relu')(x)
    x = apply_bn_and_dropout(x)
    # Предсказываем параметры распределений
    # Вместо того чтобы предсказывать стандартное отклонение, предсказываем логарифм вариации
    z_mean = Dense(latent_dim)(x)
    z_log_var = Dense(latent_dim)(x)
    # Сэмплирование из Q с трюком репараметризации
    def sampling(args):
        z_mean, z_log_var = args
        epsilon = K.random_normal(shape=(batch_size, latent_dim), mean=0., stddev=1.0)
        return z_mean + K.exp(z_log_var / 2) * epsilon
    l = Lambda(sampling, output_shape=(latent_dim,))([z_mean, z_log_var])
    models["encoder"]  = Model([input_img, input_lbl], l, 'Encoder') 
    models["z_meaner"] = Model([input_img, input_lbl], z_mean, 'Enc_z_mean')
    models["z_lvarer"] = Model([input_img, input_lbl], z_log_var, 'Enc_z_log_var')
    # Декодер
    z = Input(shape=(latent_dim, ))
    input_lbl_d = Input(shape=(num_classes,), dtype='float32')
    x = concatenate([z, input_lbl_d])
    x = Dense(256)(x)
    x = LeakyReLU()(x)
    x = apply_bn_and_dropout(x)
    x = Dense(28*28, activation='sigmoid')(x)
    decoded = Reshape((28, 28, 1))(x)
    models["decoder"] = Model([z, input_lbl_d], decoded, name='Decoder')
    models["cvae"]    = Model([input_img, input_lbl, input_lbl_d], 
                              models["decoder"]([models["encoder"]([input_img, input_lbl]), input_lbl_d]), 
                              name="CVAE")
    models["style_t"] = Model([input_img, input_lbl, input_lbl_d], 
                               models["decoder"]([models["z_meaner"]([input_img, input_lbl]), input_lbl_d]), 
                               name="style_transfer")
    def vae_loss(x, decoded):
        x = K.reshape(x, shape=(batch_size, 28*28))
        decoded = K.reshape(decoded, shape=(batch_size, 28*28))
        xent_loss = 28*28*binary_crossentropy(x, decoded)
        kl_loss = -0.5 * K.sum(1 + z_log_var - K.square(z_mean) - K.exp(z_log_var), axis=-1)
        return (xent_loss + kl_loss)/2/28/28
    return models, vae_loss
models, vae_loss = create_cvae()
cvae = models["cvae"]


from keras.optimizers import Adam, RMSprop
cvae.compile(optimizer=Adam(start_lr), loss=vae_loss)


digit_size = 28
def plot_digits(*args, invert_colors=False):
    args = [x.squeeze() for x in args]
    n = min([x.shape[0] for x in args])
    figure = np.zeros((digit_size * len(args), digit_size * n))
    for i in range(n):
        for j in range(len(args)):
            figure[j * digit_size: (j + 1) * digit_size,
                   i * digit_size: (i + 1) * digit_size] = args[j][i].squeeze()
    if invert_colors:
        figure = 1-figure
    plt.figure(figsize=(2*n, 2*len(args)))
    plt.imshow(figure, cmap='Greys_r')
    plt.grid(False)
    ax = plt.gca()
    ax.get_xaxis().set_visible(False)
    ax.get_yaxis().set_visible(False)
    plt.show()
n = 15 # Картинка с 15x15 цифр
from scipy.stats import norm
# Так как сэмплируем из N(0, I), то сетку узлов, в которых генерируем цифры, берем из обратной функции распределения
grid_x = norm.ppf(np.linspace(0.05, 0.95, n))
grid_y = norm.ppf(np.linspace(0.05, 0.95, n))
def draw_manifold(generator, lbl, show=True):
    # Рисование цифр из многообразия
    figure = np.zeros((digit_size * n, digit_size * n))
    input_lbl = np.zeros((1, 10))
    input_lbl[0, lbl] = 1
    for i, yi in enumerate(grid_x):
        for j, xi in enumerate(grid_y):
            z_sample = np.zeros((1, latent_dim))
            z_sample[:, :2] = np.array([[xi, yi]])
            x_decoded = generator.predict([z_sample, input_lbl])
            digit = x_decoded[0].squeeze()
            figure[i * digit_size: (i + 1) * digit_size,
                   j * digit_size: (j + 1) * digit_size] = digit
    if show:
        # Визуализация
        plt.figure(figsize=(10, 10))
        plt.imshow(figure, cmap='Greys_r')
        plt.grid(False)
        ax = plt.gca()
        ax.get_xaxis().set_visible(False)
        ax.get_yaxis().set_visible(False)
        plt.show()
    return figure
def draw_z_distr(z_predicted, lbl):
    # Рисование рпспределения z
    input_lbl = np.zeros((1, 10))
    input_lbl[0, lbl] = 1
    im = plt.scatter(z_predicted[:, 0], z_predicted[:, 1])
    im.axes.set_xlim(-5, 5)
    im.axes.set_ylim(-5, 5)
    plt.show()


from IPython.display import clear_output
from keras.callbacks import LambdaCallback, ReduceLROnPlateau, TensorBoard
# Массивы, в которые будем сохранять результаты для последующей визуализации
figs = [[] for x in range(num_classes)]
latent_distrs = [[] for x in range(num_classes)]
epochs = []
# Эпохи, в которые будем сохранять
save_epochs = set(list((np.arange(0, 59)**1.701).astype(np.int)) + list(range(10)))
# Отслеживать будем на вот этих цифрах
imgs = x_test[:batch_size]
imgs_lbls = y_test_cat[:batch_size]
n_compare = 10
# Модели
generator      = models["decoder"]
encoder_mean   = models["z_meaner"]
# Функция, которую будем запускать после каждой эпохи
def on_epoch_end(epoch, logs):
    if epoch in save_epochs:
        clear_output() # Не захламляем output
        # Сравнение реальных и декодированных цифр
        decoded = cvae.predict([imgs, imgs_lbls, imgs_lbls], batch_size=batch_size)
        plot_digits(imgs[:n_compare], decoded[:n_compare])
        # Рисование многообразия для рандомного y и распределения z|y
        draw_lbl = np.random.randint(0, num_classes)
        print(draw_lbl)
        for lbl in range(num_classes):
            figs[lbl].append(draw_manifold(generator, lbl, show=lbl==draw_lbl))
            idxs = y_test == lbl
            z_predicted = encoder_mean.predict([x_test[idxs], y_test_cat[idxs]], batch_size)
            latent_distrs[lbl].append(z_predicted)
            if lbl==draw_lbl:
                draw_z_distr(z_predicted, lbl)
        epochs.append(epoch)
# Коллбэки
pltfig = LambdaCallback(on_epoch_end=on_epoch_end)
# lr_red = ReduceLROnPlateau(factor=0.1, patience=25)
tb     = TensorBoard(log_dir='./logs')
# Запуск обучения 
cvae.fit([x_train, y_train_cat, y_train_cat], x_train, shuffle=True, epochs=1000,
         batch_size=batch_size,
         validation_data=([x_test, y_test_cat, y_test_cat], x_test),
         callbacks=[pltfig, tb],
         verbose=1)


results


(I apologize that in some places white numbers are on a black background, and in some places black are on white)

This auto encoder translates the numbers like this:



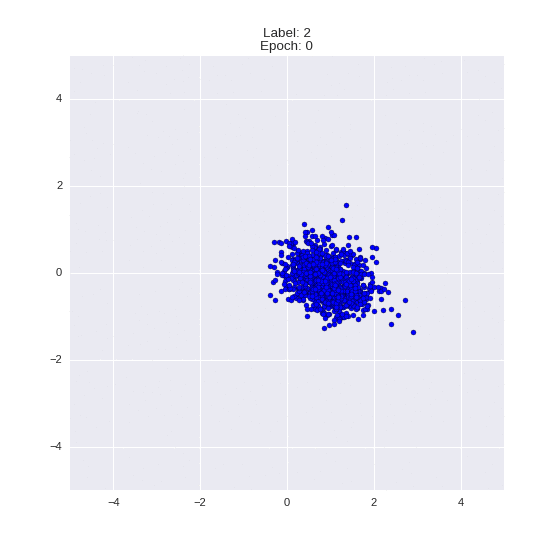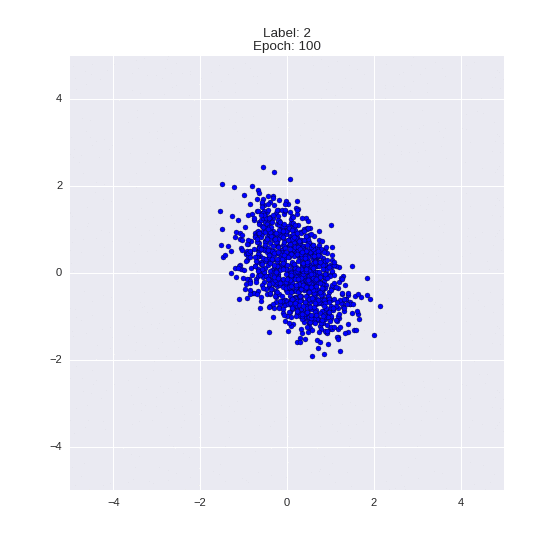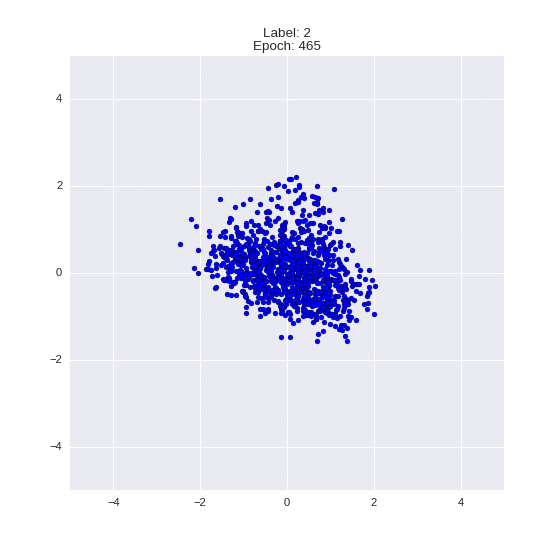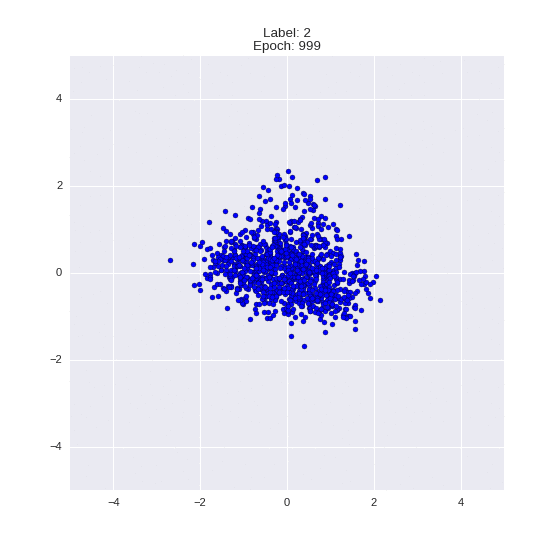
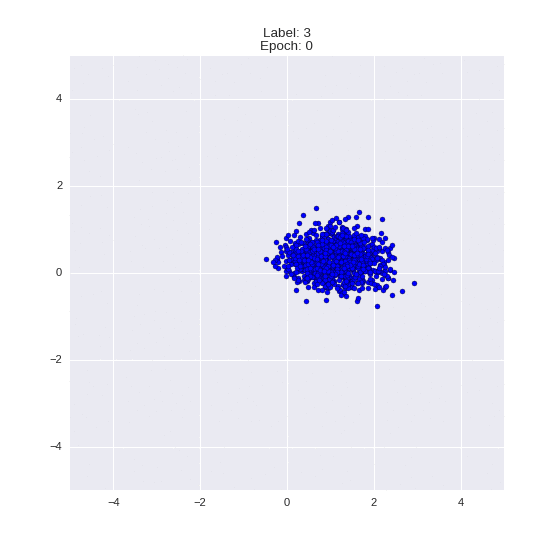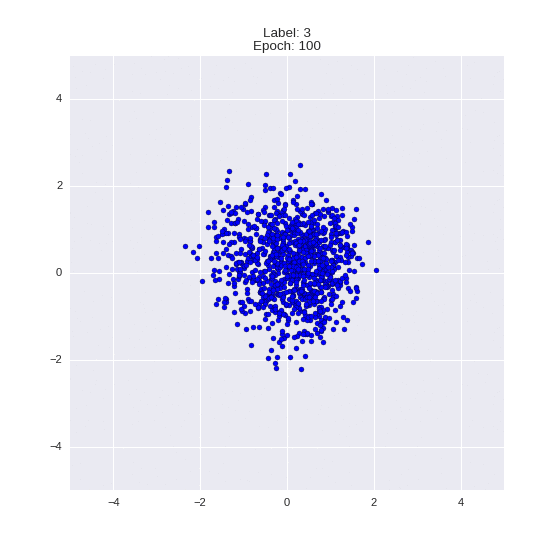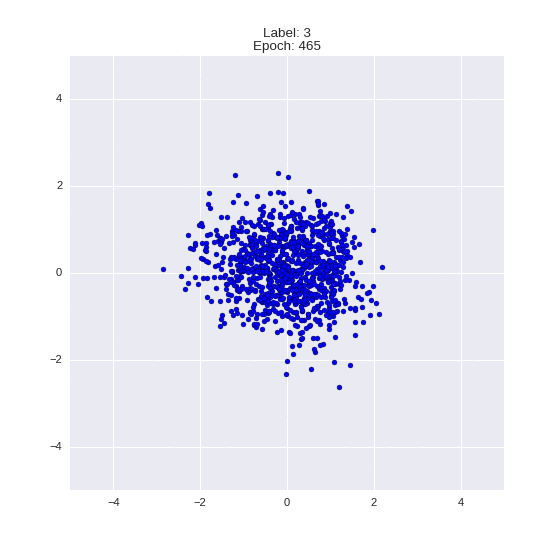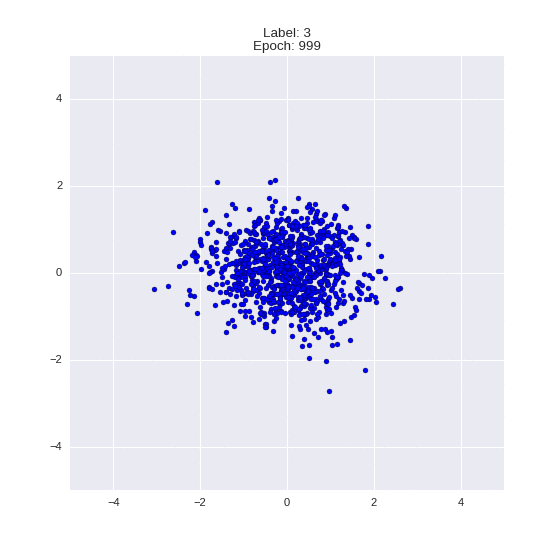
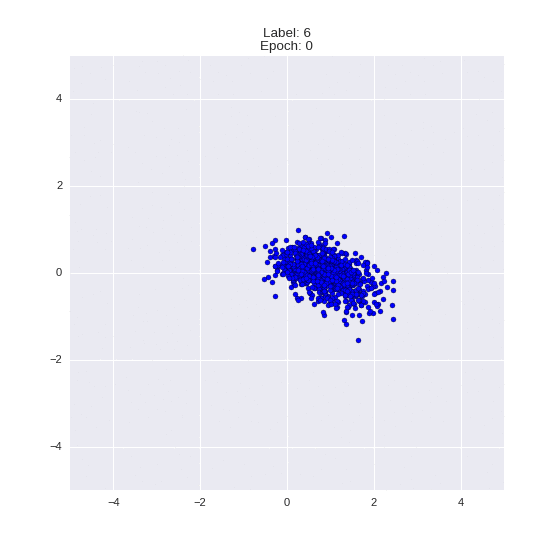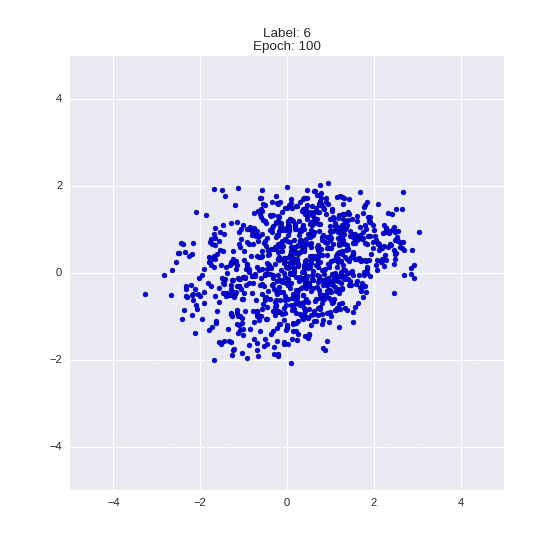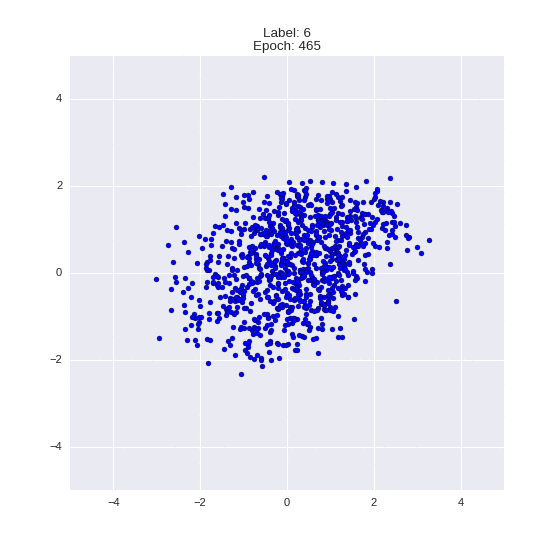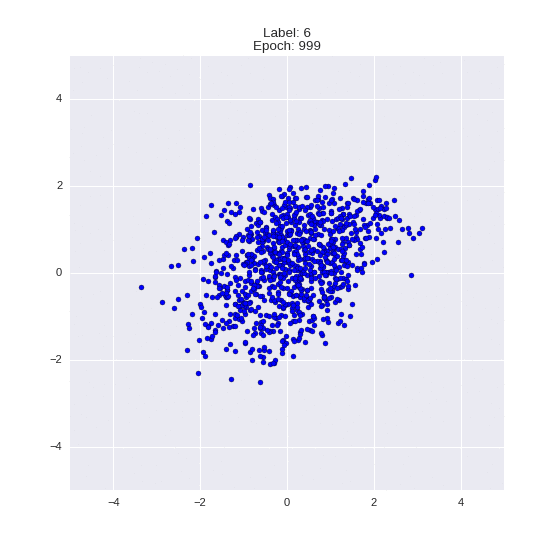
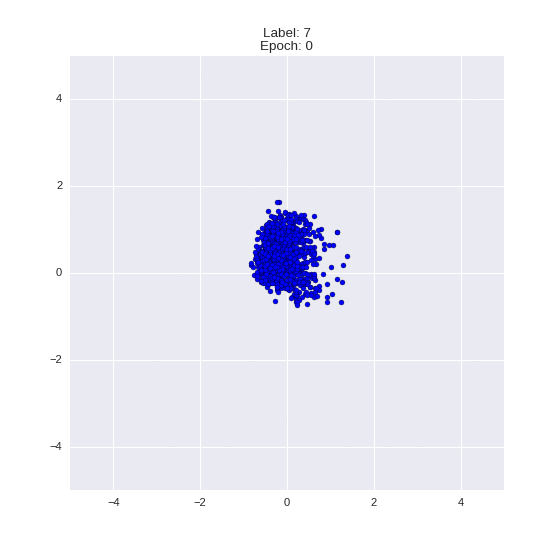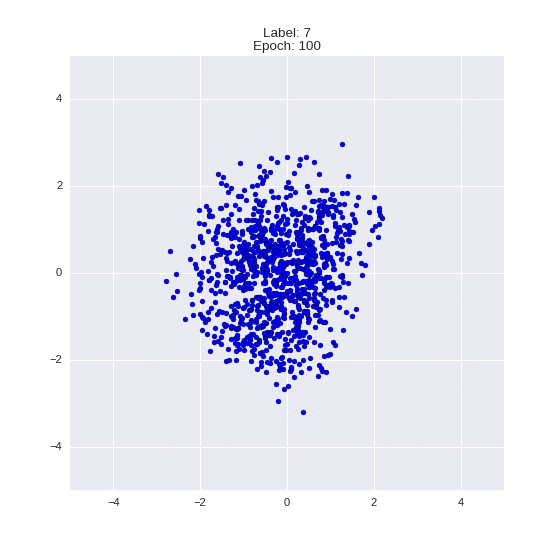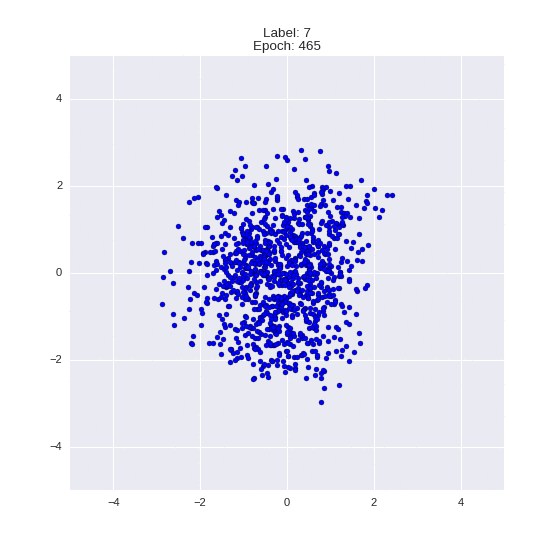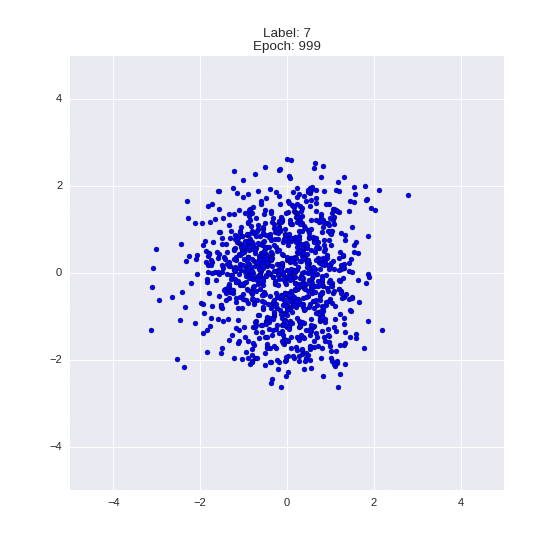
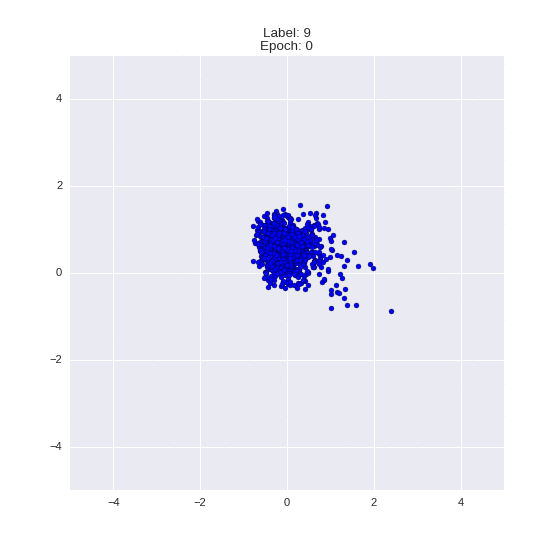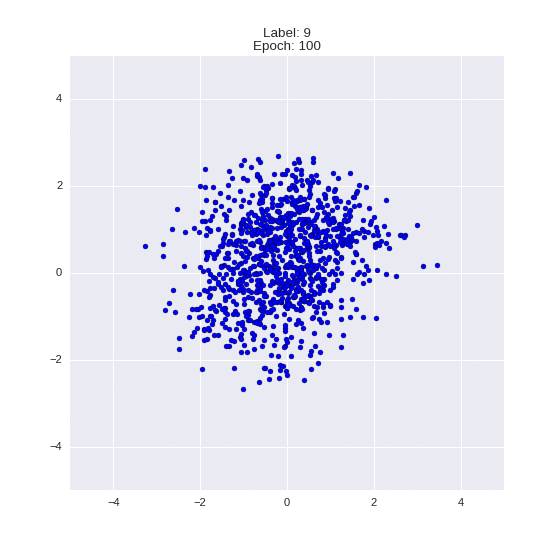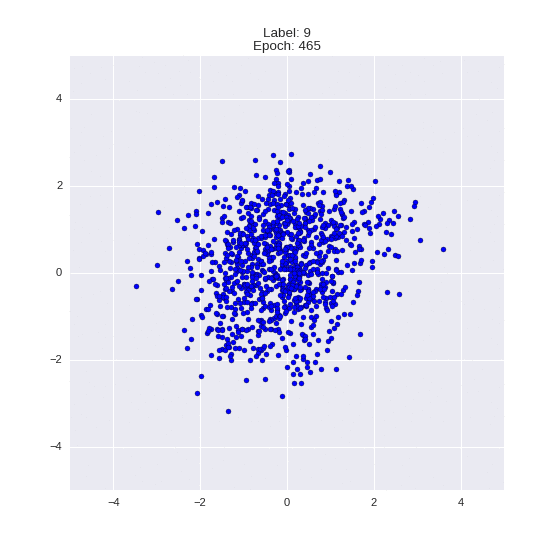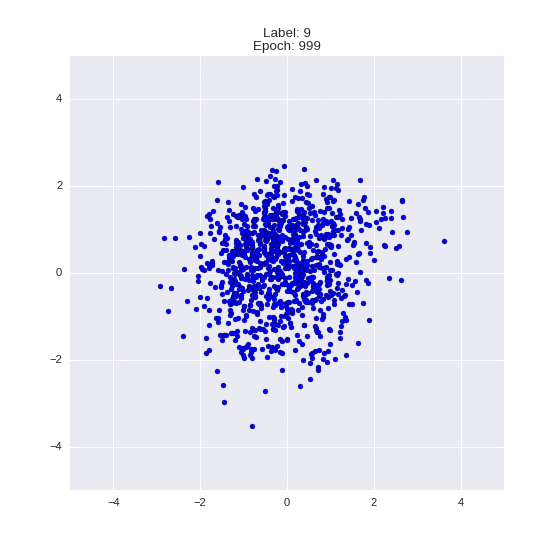
The generated numbers of each label are sampled from N (0 | I):

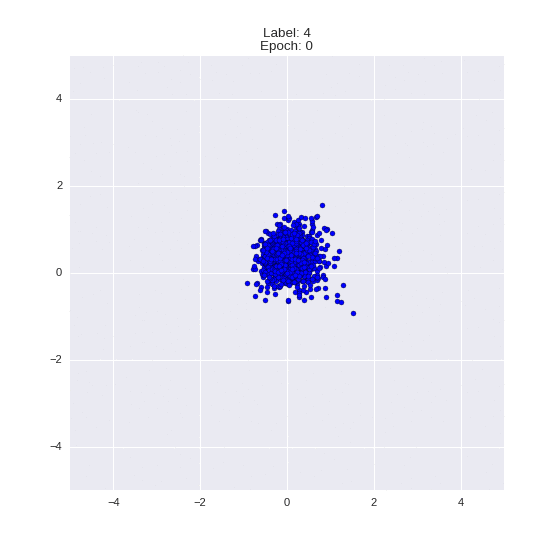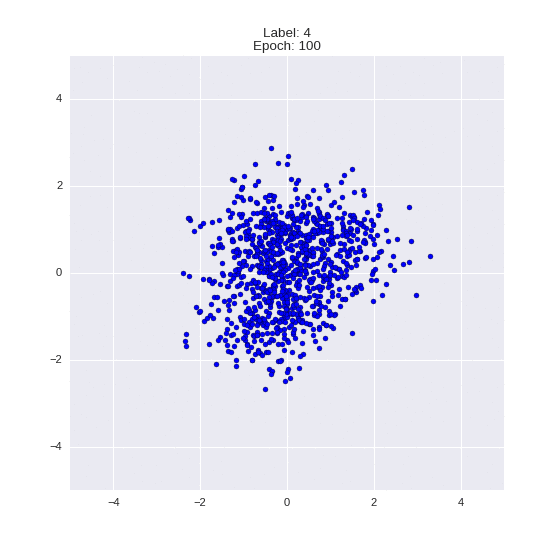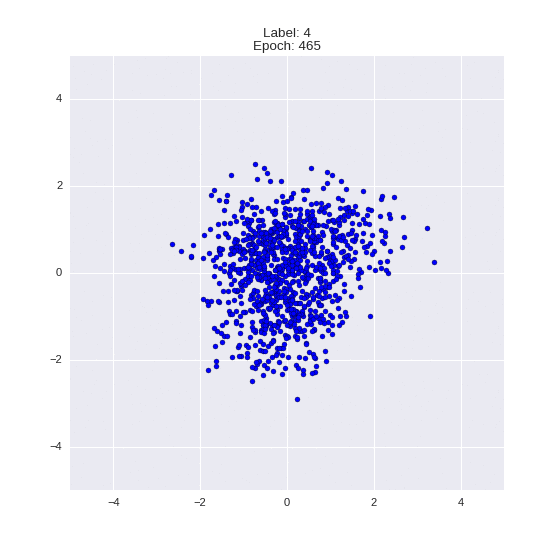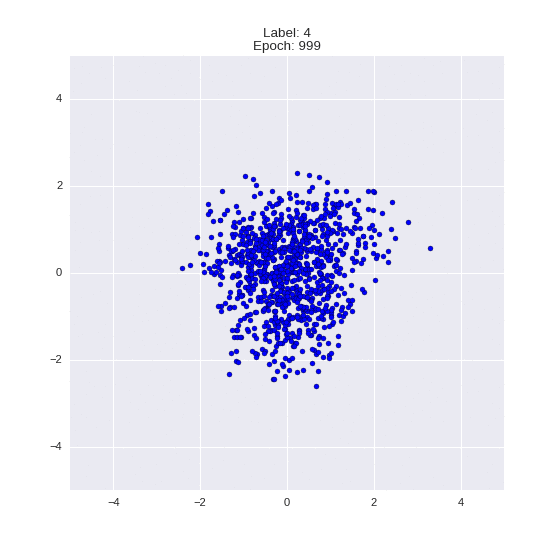
(It can be clearly seen how the common features are encoded in coordinates Z)



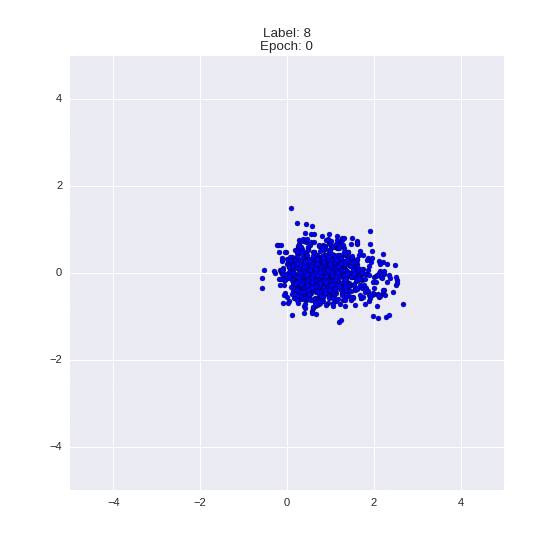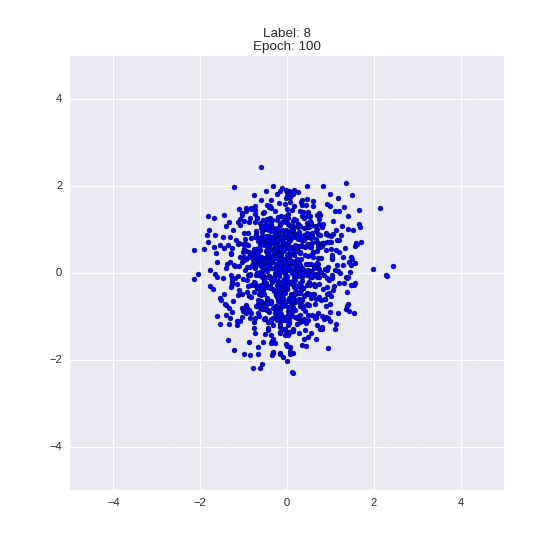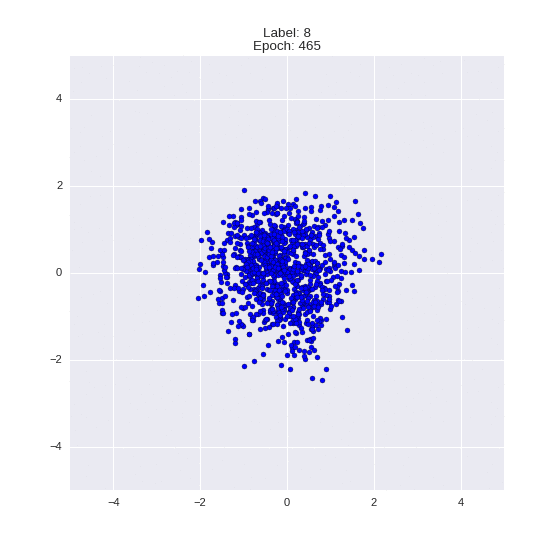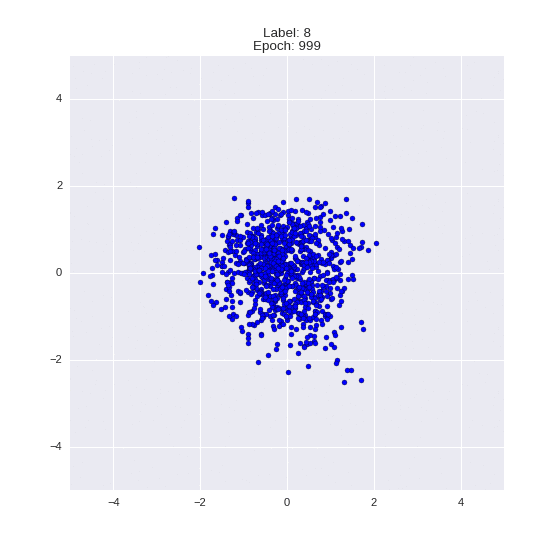
Generation of digits of a given label from Zand distribution Zfor each label


Heavy GIFs



























Wrap style with this model


As sources of style we take the first ten "7" -oks, and based on their code Zwe create the remaining digits.

The code
def style_transfer(model, X, lbl_in, lbl_out):
    rows = X.shape[0]
    if isinstance(lbl_in, int):
        lbl = lbl_in
        lbl_in = np.zeros((rows, 10))
        lbl_in[:, lbl] = 1
    if isinstance(lbl_out, int):
        lbl = lbl_out
        lbl_out = np.zeros((rows, 10))
        lbl_out[:, lbl] = 1
    return model.predict([X, lbl_in, lbl_out])



n = 10
lbl = 7
generated = []
prot = x_train[y_train == lbl][:n]
for i in range(num_classes):
    generated.append(style_transfer(models["style_t"], prot, lbl, i))
generated[lbl] = prot
plot_digits(*generated, invert_colors=True)




The style was transferred quite successfully: the slope and thickness of the stroke are preserved.

More style properties could be carried over simply by increasing the dimension Z, this would also make the numbers less blurry.

In the next part, we will look at how, using generative competing networks (GANs) , to generate numbers practically indistinguishable from real ones, and after that how to combine GANs with autoencoders.

GIF Creation Code


The code
from matplotlib.animation import FuncAnimation
from matplotlib import cm
import matplotlib
def make_2d_figs_gif(figs, epochs, c, fname, fig): 
    norm = matplotlib.colors.Normalize(vmin=0, vmax=1, clip=False)
    im = plt.imshow(np.zeros((28,28)), cmap='Greys', norm=norm)
    plt.grid(None)
    plt.title("Label: {}\nEpoch: {}".format(c, epochs[0]))
    def update(i):
        im.set_array(figs[i])
        im.axes.set_title("Label: {}\nEpoch: {}".format(c, epochs[i]))
        im.axes.get_xaxis().set_visible(False)
        im.axes.get_yaxis().set_visible(False)
        return im
    anim = FuncAnimation(fig, update, frames=range(len(figs)), interval=100)
    anim.save(fname, dpi=80, writer='imagemagick')
def make_2d_scatter_gif(zs, epochs, c, fname, fig):
    im = plt.scatter(zs[0][:, 0], zs[0][:, 1])
    plt.title("Label: {}\nEpoch: {}".format(c, epochs[0]))
    def update(i):
        fig.clear()
        im = plt.scatter(zs[i][:, 0], zs[i][:, 1])
        im.axes.set_title("Label: {}\nEpoch: {}".format(c, epochs[i]))
        im.axes.set_xlim(-5, 5)
        im.axes.set_ylim(-5, 5)
        return im
    anim = FuncAnimation(fig, update, frames=range(len(zs)), interval=100)
    anim.save(fname, dpi=80, writer='imagemagick')
for lbl in range(num_classes):
    make_2d_figs_gif(figs[lbl], epochs, lbl, "./figs4/manifold_{}.gif".format(lbl), plt.figure(figsize=(7,7)))
    make_2d_scatter_gif(latent_distrs[lbl], epochs, lbl, "./figs4/z_distr_{}.gif".format(lbl), plt.figure(figsize=(7,7)))


Useful links and literature


The theoretical part is based on the article:
[1] Tutorial on Variational Autoencoders, Carl Doersch, https://arxiv.org/abs/1606.05908
and is actually a summary of it.

Many pictures are taken from the Isaac Dykeman blog:
[2] Isaac Dykeman, http://ijdykeman.github.io/ml/2016/12/21/cvae.html

Read more about the Kullback-Leibler distance in Russian in
[3] http : //www.machinelearning.ru/wiki/images/d/d0/BMMO11_6.pdf

The code is partially based on the article by Francois Chollet :
[4] https://blog.keras.io/building-autoencoders-in-keras.html

Other interesting links:
http://blog.fastforwardlabs.com/2016/08/12/introducing-variational-autoencoders-in-prose-and.html
http://kvfrans.com/variational-autoencoders-explained/
Tags:

Also popular now: