How does a barcode work?
Hi all!
Every person is using barcodes nowadays, mostly without noticing this. When we are buying the groceries in the store, their identifiers are getting from barcodes. Its also the same with goods in the warehouses, postal parcels and so on. But not so many people actually know, how it works.
What is 'inside' the barcode, and what is encoded on this image?

Lets figure it out, and also lets write our own bar decoder.
Using barcodes has a long history. First attempts of making the automation were made in 50s, the patent for a codes reading system was granted. David Collins, who worked at the Pennsylvania Railroad, decided to make the cars sorting process easier. The idea was obvious — to encode the car identifiers with different color stripes, and read them using a photo cell. In 1962 such a codes became a standard by the Association of American Railroads. (the KarTrak system). In 1968 the lamp was replaced by a laser, it allowed to increase the accuracy and reduce the reader size. In 1973 the Universal Product Code was developed, and in 1974 the first grocery product (a Wrigley’s chewing gum — it was obviously in USA;) was sold. In 1984 third part of all stores have used barcodes, in other countries it became popular later.
There are many different barcode types for different applications, for example, «12345678» string can be encoded this ways (and its not all of them):

Lets start the analyse. All information below will be about the «Code-128» type — just because its easy to understand the principle. Those, who want to test other modes, can use online barcode generator and test other types on their own.
At first sight, a barcode looks like a random set of numbers, but in fact its structure is well organized:

1 — Empty space, required to determine the code start position.
2 — Start symbol. Three types of Code-128 are available (called A, B and C), and start symbols can be 11010000100, 11010010000 or 11010011100 respectively. For this types, the encoding tables are different (see Code_128 description for more details).
3 — The code itself, containing user data.
4 — Check sum.
5 — Stop symbol, for Code-128 its 1100011101011.
6(1) — Empty space.
Now lets have a look, how the bits are encoding. Its really easy — if we will take the thinnest line width to «1», then double width line will be «11», triple width line is «111», and so on. The empty space will be respectively «0», «00» or «000», according to the same principle. Those who interested, can compare the start sequence on the image above, to see that the rule is respected.
Now we can start coding.
In general, its the most complicated part, and it can be done different ways. I am not sure that my approach is optimal, but for our task its definitely enough.
First, lets load the image, stretch its width, crop a horizontal line from the middle, convert it to b/w color and save it as an array.
On the barcode black line corresponds to «1», but in RGB the black is in contrary, 0, so the array needs to be inverted. We will also calculate the average value.
Lets run the program to verify that the barcode was correctly loaded:
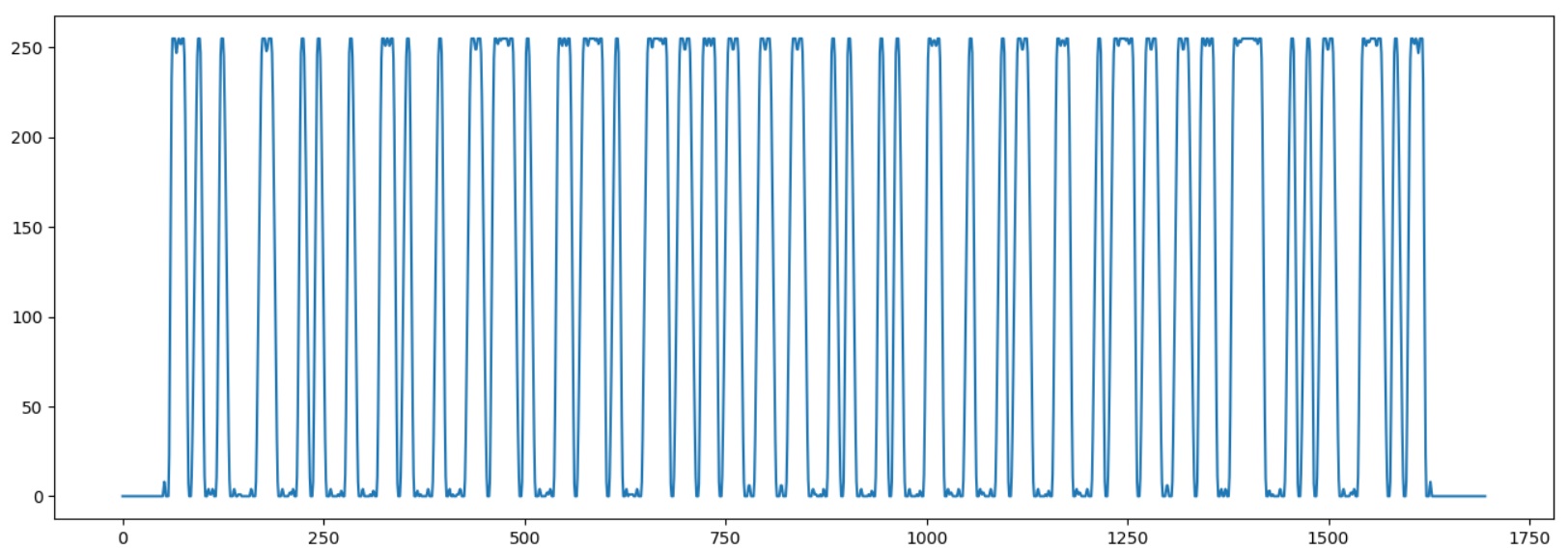
Now we need to determine a width of one 'bit'. To do this, we will extract the sequence, saving the positions of the average line crossing.
We are saving only the average line crossings, so the code «1101» will be saved as «101», bit its enough to get its pixels width.
Now lets make the decoding itself. We need to find every average line crossing, and find the number of bits in the last interval, that was found. Numbers will not match perfect (the code can be stretched or bent a bit), so, we need to round the value to integer.
Maybe there is a better way to do this, readers can write in comments.
If all was done perfect, we will get a sequence like this:
In general, its pretty easy. Symbols in the Code-128 are encoded with 11-bit code, that can have different encoding (according to this encoding — A, B or С, it can be letters or digits from 00 to 99).
In our case, the beginning of the sequence is 11010010000, that corresponds to a «Code B». I was too lazy to enter all codes manually, so I just copy-pasted it from a Wikipedia page. Parsing of this lines was also made on Python (hint — don't do things like this on production).
The last parts are easy. First, lets split the sequence to 11-bit blocks:
Finally, lets generate the output string and display it:
I will not show here the decoded result from the top image, let it be the homework for readers (using the downloaded apps for smartphones will be considered cheating:).
CRC check is not implemented in this code, those who want, can do it themselves.
For sure, this algorithm is not perfect, it was done in half an hour. For professional tasks there are ready-to-use libraries, for example, pyzbar. For decoding the image, 4 lines of code is enough:
(first the library has to be installed using command «pip install pyzbar»)
Addition: site user vinograd19 sent an interesting comment about the barcode check sum calculation history.
The check number calculation is interesting, it originated evolutionarily.
Check sum is obviously needed to avoid wrong decoding. If the barcode was 1234, and was decoded as 7234, we need a method to reject replacing 1 to 7. The validation can be not perfect, but at least 90% of codes should be verified correctly.
1st approach: Lets just take the sum, to have 0 as the remainder of the division. First symbols contains data, and the last digit is is chosen so, that the sum of all numbers is divided by 10. After decoding, if the amount is not divisible by 10 — the decoding is incorrect, and needs to be repeated. For example, the code 1234 is valid — 1+2+3+4 = 10. Code 1216 — is also valid, but 1218 is not.
It helps to avoid decoding problems. But the codes can be also entered manually, using the hardware keyboard. Using this, another bad case was found — if the order of two digits will be changed, the check sum will be still correct, its definitely bad. For example, if the barcode 1234 was entered as 2134, the check sum will be the same. It was found, that a wrong digit order was the common case, if a person is trying to enter digits fast.
2nd approach. Lets improve the checksum algorithm — lets calculate the odd numbers twice. Then, if the order will be changed, the sum will be incorrect. For example, the code 2364 is valid (2 + 3*2 + 6 + 4*2 = 20), but the code 3264 is not (3 + 2*2 + 6 + 4*2 = 19). Its better, but another case has appeared. There are some keyboards, having 10 keys in two rows, first row is 12345 and the second is 67890. If instead of «1» user will type «2», the checksum check will be failed. But if the user will enter «6» instead of «1» — check sum may be sometimes correct. Its because 6=1+5, and if the digit has an odd place, we getting 2*6 = 2*1 + 2*5 — the sum has increased by 10. The same error will happen, if user will enter «7» instead of «2», «8» instead of «3», and so on.
3rd approach. Lets take the sum again, but lets get odd numbers… 3 times. For example, the code 1234565 — is valid, because 1 + 2*3 + 3 + 4*3 + 5 + 6*3 +5 = 50.
This method became a standard for EAN13 code, with some changes: number of digits is fixed and equal to 13, where 13th digit — is the check sum. Numbers on odd places are counted three times, on even places once.
By the way, the EAN-13 code is the most widely used in trading and shopping malls, so people see it more often than other code types. Its bit encoding is the same as in Code-128, the data structure can be found in the Wikipedia article.
As we can see, even such an easy thing as a barcode, can contain some cool stuff. By the way, another small lifehack for readers, who were patient enough to read until this place — the text under the barcode is fully identical to the barcode data. It was made for the operators, who can manually enter the code, if its not readable by scanner. So its easy to know the barcode content — just read the text below.
Thanks for reading.
Every person is using barcodes nowadays, mostly without noticing this. When we are buying the groceries in the store, their identifiers are getting from barcodes. Its also the same with goods in the warehouses, postal parcels and so on. But not so many people actually know, how it works.
What is 'inside' the barcode, and what is encoded on this image?

Lets figure it out, and also lets write our own bar decoder.
Introduction
Using barcodes has a long history. First attempts of making the automation were made in 50s, the patent for a codes reading system was granted. David Collins, who worked at the Pennsylvania Railroad, decided to make the cars sorting process easier. The idea was obvious — to encode the car identifiers with different color stripes, and read them using a photo cell. In 1962 such a codes became a standard by the Association of American Railroads. (the KarTrak system). In 1968 the lamp was replaced by a laser, it allowed to increase the accuracy and reduce the reader size. In 1973 the Universal Product Code was developed, and in 1974 the first grocery product (a Wrigley’s chewing gum — it was obviously in USA;) was sold. In 1984 third part of all stores have used barcodes, in other countries it became popular later.
There are many different barcode types for different applications, for example, «12345678» string can be encoded this ways (and its not all of them):

Lets start the analyse. All information below will be about the «Code-128» type — just because its easy to understand the principle. Those, who want to test other modes, can use online barcode generator and test other types on their own.
At first sight, a barcode looks like a random set of numbers, but in fact its structure is well organized:

1 — Empty space, required to determine the code start position.
2 — Start symbol. Three types of Code-128 are available (called A, B and C), and start symbols can be 11010000100, 11010010000 or 11010011100 respectively. For this types, the encoding tables are different (see Code_128 description for more details).
3 — The code itself, containing user data.
4 — Check sum.
5 — Stop symbol, for Code-128 its 1100011101011.
6(1) — Empty space.
Now lets have a look, how the bits are encoding. Its really easy — if we will take the thinnest line width to «1», then double width line will be «11», triple width line is «111», and so on. The empty space will be respectively «0», «00» or «000», according to the same principle. Those who interested, can compare the start sequence on the image above, to see that the rule is respected.
Now we can start coding.
Getting the bit sequence
In general, its the most complicated part, and it can be done different ways. I am not sure that my approach is optimal, but for our task its definitely enough.
First, lets load the image, stretch its width, crop a horizontal line from the middle, convert it to b/w color and save it as an array.
from PIL import Image
import numpy as np
import matplotlib.pyplot as plt
image_path = "barcode.jpg"
img = Image.open(image_path)
width, height = img.size
basewidth = 4*width
img = img.resize((basewidth, height), Image.ANTIALIAS)
hor_line_bw = img.crop((0, int(height/2), basewidth, int(height/2) + 1)).convert('L')
hor_data = np.asarray(hor_line_bw, dtype="int32")[0]
On the barcode black line corresponds to «1», but in RGB the black is in contrary, 0, so the array needs to be inverted. We will also calculate the average value.
hor_data = 255 - hor_data
avg = np.average(hor_data)
plt.plot(hor_data)
plt.show()
Lets run the program to verify that the barcode was correctly loaded:

Now we need to determine a width of one 'bit'. To do this, we will extract the sequence, saving the positions of the average line crossing.
pos1, pos2 = -1, -1
bits = ""for p in range(basewidth - 2):
if hor_data[p] < avg and hor_data[p + 1] > avg:
bits += "1"if pos1 == -1:
pos1 = p
if bits == "101":
pos2 = p
breakif hor_data[p] > avg and hor_data[p + 1] < avg:
bits += "0"
bit_width = int((pos2 - pos1)/3)
We are saving only the average line crossings, so the code «1101» will be saved as «101», bit its enough to get its pixels width.
Now lets make the decoding itself. We need to find every average line crossing, and find the number of bits in the last interval, that was found. Numbers will not match perfect (the code can be stretched or bent a bit), so, we need to round the value to integer.
bits = ""for p in range(basewidth - 2):
if hor_data[p] > avg and hor_data[p + 1] < avg:
interval = p - pos1
cnt = interval/bit_width
bits += "1"*int(round(cnt))
pos1 = p
if hor_data[p] < avg and hor_data[p + 1] > avg:
interval = p - pos1
cnt = interval/bit_width
bits += "0"*int(round(cnt))
pos1 = p
Maybe there is a better way to do this, readers can write in comments.
If all was done perfect, we will get a sequence like this:
11010010000110001010001000110100010001101110100011011101000111011011
01100110011000101000101000110001000101100011000101110110011011001111
00010101100011101011Decoding
In general, its pretty easy. Symbols in the Code-128 are encoded with 11-bit code, that can have different encoding (according to this encoding — A, B or С, it can be letters or digits from 00 to 99).
In our case, the beginning of the sequence is 11010010000, that corresponds to a «Code B». I was too lazy to enter all codes manually, so I just copy-pasted it from a Wikipedia page. Parsing of this lines was also made on Python (hint — don't do things like this on production).
CODE128_CHART = """
0 _ _ 00 32 S 11011001100 212222
1 ! ! 01 33 ! 11001101100 222122
2 " " 02 34 " 11001100110 222221
3 # # 03 35 # 10010011000 121223
...
93 GS } 93 125 } 10100011110 111341
94 RS ~ 94 126 ~ 10001011110 131141
103 Start Start A 208 SCA 11010000100 211412
104 Start Start B 209 SCB 11010010000 211214
105 Start Start C 210 SCC 11010011100 211232
106 Stop Stop - - - 11000111010 233111""".split()
SYMBOLS = [value for value in CODE128_CHART[6::8]]
VALUESB = [value for value in CODE128_CHART[2::8]]
CODE128B = dict(zip(SYMBOLS, VALUESB))
The last parts are easy. First, lets split the sequence to 11-bit blocks:
sym_len = 11
symbols = [bits[i:i+sym_len] for i in range(0, len(bits), sym_len)]
Finally, lets generate the output string and display it:
str_out = ""for sym in symbols:
if CODE128A[sym] == 'Start':
continueif CODE128A[sym] == 'Stop':
break
str_out += CODE128A[sym]
print(" ", sym, CODE128A[sym])
print("Str:", str_out)
I will not show here the decoded result from the top image, let it be the homework for readers (using the downloaded apps for smartphones will be considered cheating:).
CRC check is not implemented in this code, those who want, can do it themselves.
For sure, this algorithm is not perfect, it was done in half an hour. For professional tasks there are ready-to-use libraries, for example, pyzbar. For decoding the image, 4 lines of code is enough:
from pyzbar.pyzbar import decode
img = Image.open(image_path)
decode = decode(img)
print(decode)
(first the library has to be installed using command «pip install pyzbar»)
Addition: site user vinograd19 sent an interesting comment about the barcode check sum calculation history.
The check number calculation is interesting, it originated evolutionarily.
Check sum is obviously needed to avoid wrong decoding. If the barcode was 1234, and was decoded as 7234, we need a method to reject replacing 1 to 7. The validation can be not perfect, but at least 90% of codes should be verified correctly.
1st approach: Lets just take the sum, to have 0 as the remainder of the division. First symbols contains data, and the last digit is is chosen so, that the sum of all numbers is divided by 10. After decoding, if the amount is not divisible by 10 — the decoding is incorrect, and needs to be repeated. For example, the code 1234 is valid — 1+2+3+4 = 10. Code 1216 — is also valid, but 1218 is not.
It helps to avoid decoding problems. But the codes can be also entered manually, using the hardware keyboard. Using this, another bad case was found — if the order of two digits will be changed, the check sum will be still correct, its definitely bad. For example, if the barcode 1234 was entered as 2134, the check sum will be the same. It was found, that a wrong digit order was the common case, if a person is trying to enter digits fast.
2nd approach. Lets improve the checksum algorithm — lets calculate the odd numbers twice. Then, if the order will be changed, the sum will be incorrect. For example, the code 2364 is valid (2 + 3*2 + 6 + 4*2 = 20), but the code 3264 is not (3 + 2*2 + 6 + 4*2 = 19). Its better, but another case has appeared. There are some keyboards, having 10 keys in two rows, first row is 12345 and the second is 67890. If instead of «1» user will type «2», the checksum check will be failed. But if the user will enter «6» instead of «1» — check sum may be sometimes correct. Its because 6=1+5, and if the digit has an odd place, we getting 2*6 = 2*1 + 2*5 — the sum has increased by 10. The same error will happen, if user will enter «7» instead of «2», «8» instead of «3», and so on.
3rd approach. Lets take the sum again, but lets get odd numbers… 3 times. For example, the code 1234565 — is valid, because 1 + 2*3 + 3 + 4*3 + 5 + 6*3 +5 = 50.
This method became a standard for EAN13 code, with some changes: number of digits is fixed and equal to 13, where 13th digit — is the check sum. Numbers on odd places are counted three times, on even places once.
By the way, the EAN-13 code is the most widely used in trading and shopping malls, so people see it more often than other code types. Its bit encoding is the same as in Code-128, the data structure can be found in the Wikipedia article.
Conclusion
As we can see, even such an easy thing as a barcode, can contain some cool stuff. By the way, another small lifehack for readers, who were patient enough to read until this place — the text under the barcode is fully identical to the barcode data. It was made for the operators, who can manually enter the code, if its not readable by scanner. So its easy to know the barcode content — just read the text below.
Thanks for reading.
