Which map is faster, and is there an alternative to Judy

Shot from Top Gear: USA (Series 2)
In our most heavily loaded services, at Badoo we use the C language and sometimes C ++. Often these services store hundreds of gigabytes of data in memory and process hundreds of thousands of requests per second. And it is important for us to use not only suitable algorithms and data structures, but also their productive implementations.
Almost from the very beginning, we used Judy as an implementation of associative arrays . It has a C-interface and many advantages. We even use a wrapper for PHP, since in versions of PHP prior to 7.0 Judy greatly outperforms the amount of memory consumed compared to the built-in maps.
However, time passes, and many years have passed since the last release of Judy - it's time to look at the alternatives.
My name is Marco, I am a Badoo system programmer in the Platform team. My colleagues and I did a little research looking for alternatives to Judy, made conclusions, and decided to share them with you.
Associative array
If you know what an associative array , tree and hash table are, you can safely skip this section. For the rest - a small introduction to the topic.
An associative array is an abstract data type that allows a key to receive or store a value. It is abstract because it says nothing about how this data type should be implemented. Indeed, if you think a little, you can come up with dozens of different implementations of different levels of adequacy.
For example, we can take a banal linked list . On put, we will go around it all from beginning to end to make sure that we do not have such an element yet, and if not, add it to the end of the list; on get - just go around the list from beginning to end in search of the desired item. The algorithmic complexity of finding and adding an element to such an associative array is O (n), which is not very good.
From simple, but slightly more adequate implementations, we can consider a simple array , the elements of which we will always keep sorted by key. You can search in such an array by binary search , getting O (log (n)), but adding elements to it may require copying large pieces of memory due to the need to free up space for the element in a strictly defined position.
If we look at how associative arrays are implemented in practice, then most likely we will see some kind of tree or hash table .
Hash table
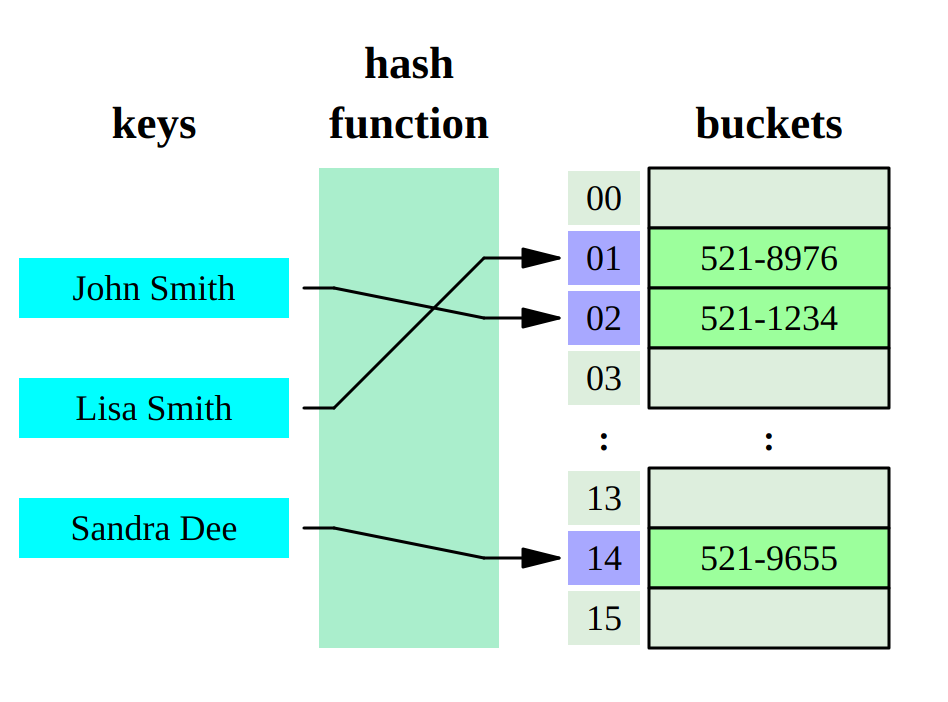
A hash table is a data structure that implements an associative array, the device of which is a two-stage process.
At the first stage, our key is run through a hash function . This is a function that takes a set of bytes (our key) at the input, and usually gives some kind of output at the output. In the second stage, we use this number to search for the value.
How? There are many options. The first thing that comes to mind is to use this number as an index in a regular array. The array in which our values lie. But this option will not work for at least two reasons:
The range of values of the hash function is most likely larger than the size of the array that we would like to keep allocated in memory.
- Hash functions have collisions: two different keys can give the same number in the response.
Both of these problems are usually solved by allocating an array of limited size, each element of which is a pointer to another array (bucket). The range of values of our hash function we then map to the size of the first array.
How? Again, there are many options. For example, take the remainder of dividing by the size of the array, or simply take the desired number of the least significant bits of the number if the size of the array is a power of two (the remainder of dividing is a much slower operation for the processor compared to the shift, so arrays with size being a power of two).
I gave as an example one of the most common ways to implement a hash table, but in general there are a great many of them. And depending on the chosen method of dealing with collisions, we will get different performance. If we talk about algorithmic complexity for hash tables, then on average we will have O (1), and in degenerate cases (worst case), O (n) can also turn out.
Trees
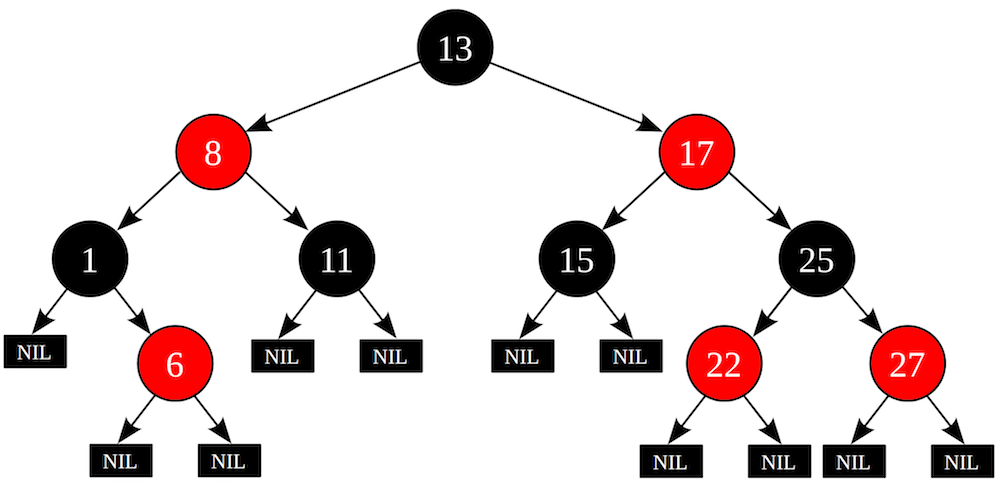
With trees, everything is pretty simple. To implement associative arrays, various binary trees are used - such as, for example, red-black tree . If the tree is balanced, we get O (log n) per operation.
Some tree implementations, such as google btree , take into account the modern memory hierarchy and store keys in batches for more efficient use of processor caches.
Trees make it possible to bypass elements in ascending or descending order of keys, which is often a very important condition when choosing an implementation. Hash tables do not know how.
What are we looking at?
The world of associative arrays, of course, is not black and white: each implementation has both advantages and disadvantages.
Different implementations may differ not only in performance, but also in the set of functions provided. For example, some implementations allow you to bypass elements in ascending or descending order of the key, while some do not. And this limitation is connected with the internal architecture, and not with the whims of the author.
Yes, and banal performance can vary greatly depending on how you use the associative array: basically write to it or read, read keys in random order or sequentially.
Gone are the days when Knut's O-notations were enough to compare two algorithms. The real world is much more complicated. The modern hardware that our programs run on has a multi-level memory , access to different levels of which is very different, and taking this into account can speed up the algorithm several times or slow it down as much.
An important criterion is the question of memory consumption: what is the overhead of the selected implementation compared to the theoretical minimum (key size + value size multiplied by the number of elements) and is such an overhead acceptable in our program?
Pauses, maximum latency and responsiveness also play an important role. Some implementations of associative arrays require a one-time expensive rebuild of their internal structures when adding an element that is unlucky, while others “smear” these time delays.
Study participants
Judy
Judy (or Judy Array) is a structure invented by Douglas Baskins that implements an ordered associative array. The implementation is written in C and is extremely complex. The author tried to take into account modern architecture and use processor caches to the maximum.
Judy is a tree, not a hash table. And not just a tree, but the so-called prefix tree . For us consumers, this means that using Judy, we get key compression and the ability to run through the elements in ascending or descending order of the key.
Judy provides several key / value variations:
| Variation | Key | Value |
|---|---|---|
| Judy1 | uint64_t | bit |
| JudyL | uint64_t | uint64_t |
| Judysl | null-terminated string | uint64_t |
| Judyhs | array of bytes | uint64_t |
Judy1 useful for large sparse the bitmap 's. JudyL is the basic type that we most often use in Badoo C-services. JudySL, as you can see, is convenient to use for strings, and JudyHL is just for some set of bytes.
std :: unordered_map
unordered_map is implemented in C ++ as a template, so anything and everything can be used as a key and value. If you use non-standard types, you will have to define a function to hash these types.
This is the hash table, so key bypass in ascending or descending order is not available.
google :: sparse_hash_map
As the name implies, sparse hash was developed by Google and claims a minimum overhead of only two bits per value. It is also implemented in C ++ and made as a template (and this, in my opinion, is an obvious advantage of C ++ implementations).
Among other things, sparse hash can save its state to disk and boot from it.
google :: dense_hash_map
In addition to sparse hash, Google made an option called dense hash. The speed of it (and especially the speed of get'a) is much higher, but you have to pay a lot of memory for this. Also, because dense_hash_map has flat arrays inside, expensive rebuilding is required periodically. By the way, Konstantin Osipov spoke about such problems and nuances of hash tables in his report on HighLoad ++ . I recommend to study.
If the amount of data that you store in the associative array is small and its size will not change much, dense hash should suit you best.
Similarly, sparse hash dense hash is a hash table and template. That is, I repeat, no passing through the keys in ascending order, but at the same time the ability to use any types as keys and values.
Also, similar to its counterpart sparse_hash_map dense_hash_map can save its state to disk.
spp :: sparse_hash_map
And finally, the last applicant from one of the developers google sparse hash. The author took sparse hash as a basis and rethought it, achieving a minimum overhead of one bit per record.
All the same: hash table and template. C ++ implementation.
Applicants submitted - it's time to check what they are capable of.
Two more factors
But first, I note that two more things will affect the performance and memory consumption.
Hash function
All participants in our study, which are hash tables, use hash functions.
Hash functions have quite a few properties, each of which may be more or less important depending on the area. For example, in cryptography, it is important that a minimal change in the input data leads to the largest possible change in the result.
But we are most interested in speed. The performance of the hash functions can vary greatly, and the speed often depends on the amount of data that it "feeds". When a long chain of bytes is supplied to the hash function, it may be advisable to use SIMD instructions to more efficiently use the capabilities of modern processors.
In addition to the standard hash function from C ++, I'll see how xxhash and t1ha do it .
Memory allocation
The second factor that will definitely affect our results is a memory allocator. The speed of work and the amount of memory consumed directly depend on it. The standard libc allocator is jack of all trades . It is good for everything, but not perfect for anything.
As an alternative, I will consider jemalloc . Despite the fact that in the test we will not take advantage of one of its main advantages - work with multithreading - I expect faster work with this allocator.
results
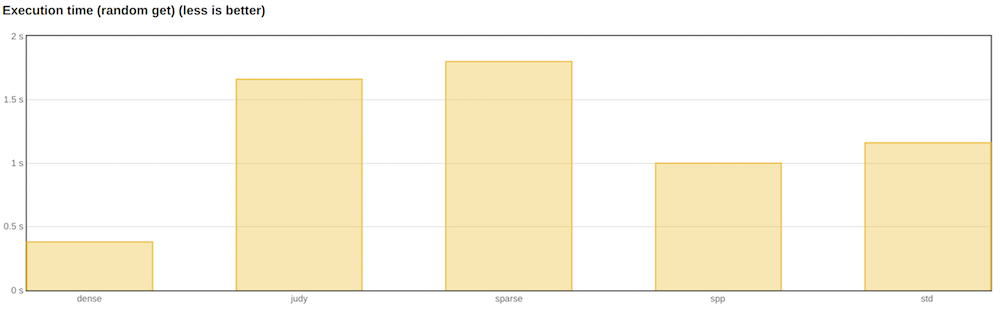
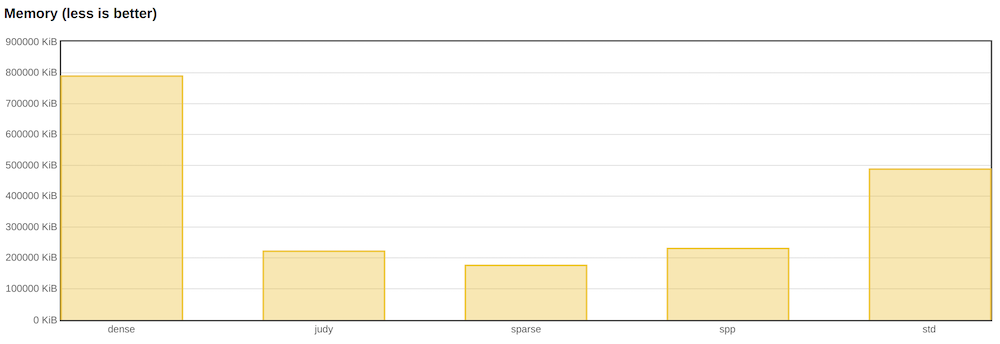
Below are the results of a random search test among ten million elements. The two parameters that interest me the most are the test execution time and the maximum memory consumed (RSS of the process at its peak).
I used a 32-bit integer as the key, and a pointer (64 bits) as the value. It is these sizes of keys and values that we most often use.
I did not show the results of other tests that are presented in the repository, since I was most interested in the random get and memory consumption.
The fastest associative array was dense hash from Google. Next comes spp, and then std :: unordered_map.
However, if you look at the memory, you can see that dense_hash_map consumes it more than all other implementations. Actually, this is what the documentation says. Moreover, if we had competing read and write in the test, we would most likely encounter a stop-the-world rebuild. Thus, in applications where responsiveness and many entries are important, dense hash cannot be used.
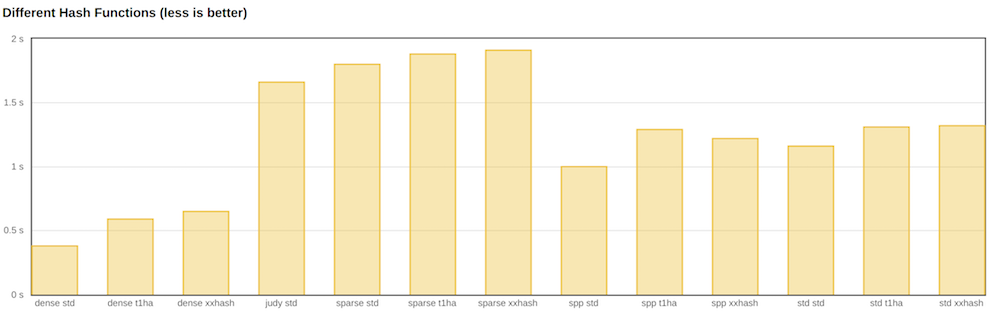
I also looked at alternative hash function implementations. But as it turned out, the standard std :: hash is faster.
A colleague accidentally noticed that in the case of 32- or 64-bit keys, std :: hash is essentially just identity. That is, the input and output are the same number, or, in other words, the function does nothing. xhash and t1ha honestly consider a hash.
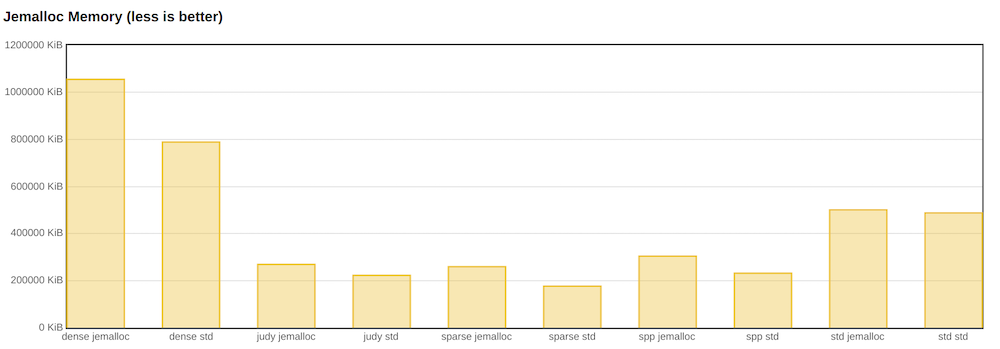
In terms of performance, jemalloc is useful. Almost all implementations become faster.
However, jemalloc is not so good at consuming memory.
Source code and hardware
I posted the source code of the benchmarks on github . If you wish, you can repeat my tests or expand them.
I tested on my home desktop:
- Ubuntu 17.04
- Linux 4.10.0
- Intel® Core (TM) i7-6700K CPU @ 4.00GHz
- 32 GiB DDR4 memory
- GCC 6.3.0
- Compiler flags: -std = c ++ 11 -O3 -ffast-math
Brief Conclusions and Final Words
Our tests showed the good potential of spp as a substitute for Judy. spp turned out to be faster on random get'ahs, and its memory overhead is not too large.
We made a simple wrapper over C ++ for C and in the near future we will try spp in one of our highly loaded services.
Well, as a philosophical conclusion, I’ll say that each of the implementations we have considered has its pros and cons and should be chosen based on the task at hand. Understanding their internal structure will help you to compare the task and the solution, and this understanding often distinguishes a simple engineer from an advanced one.