The implementation of pseudo-3D in racing games

Introduction

Why pseudo-3d?

Why would anyone want to create old-school-style roads today, when every computer can draw on-the-fly graphics consisting of millions of polygons? Are polygons not the same, only better? Not really. Polygons do create less distortion, but it is the deformations in the old game engines that give such a surreal, dizzying sense of speed, felt in many pre-polygonal games. Imagine the scope being controlled by a camera. When moving along a curve in a game using one of these engines, it looks like she is looking at the curve. Then, when the road becomes straight, the view also straightens out. When driving in a bend with poor visibility, the camera seems to be peering over a ledge. And since such games do not use the traditional track format with exact spatial relationships, you can easily create tracks on which the player will ride at breathtaking speed. You don’t need to worry about objects appearing on the track faster than the player can react, because the physical reality of the game can be easily changed in accordance with the style of the gameplay.

But in such a system there are many shortcomings. The depth of physics used in simulation games will be lost, so these engines are not suitable for these games. However, they are easy to implement, work quickly, and games based on them are usually very interesting!

It is worth noting that not every old racing game uses these techniques. In fact, the method described in the article is only one way to create a pseudo-three-dimensional road. In other cases, projected and scaled sprites or various methods of real projecting the road are used. The degree to which real math is mixed with tricks depends on the creators. I hope you enjoy exploring the special effect I have proposed.

How well do you need to understand math?

If you…

... you know trigonometry, then it will be enough to understand the whole tutorial
... you only know algebra and geometry, then skip the explanation of "scope"
... you want to avoid mathematical explanations, then read the sections "The simplest road", "Curves and turns", "Sprites and data ”and“ Hills ”.

This is a universal technique, and you can understand in more detail by simply adding the appropriate sections. If you know complex mathematics, then it will be interesting to you, but if you understand only arithmetic, you can reach the level of detail created in games such as Pole Position or in the first OutRun.

How well do you need to know programming?

If you understand bitmap graphics, this will help a lot: just know what a scanline is, and that each line consists of a series of pixels. Sample programs are written in pseudocode, so knowledge of a specific language is not required.

Ready? Let's get started!

Raster effects: a small introduction

A pseudo-three-dimensional road is one of the cases of a more general class of effects called raster effects. The most famous of the raster effects used in Street Fighter II: when you move the fighters left or right, the surface of the earth changes in perspective. But this is not really 3D. Surface graphics are stored as a very wide-angle shot. When scrolling, the lines of the screen that are “further” move more slowly than the closer ones. That is, each line on the screen moves independently of the other. The final result and how the graphics of the surface of the earth are stored in memory are shown below.

Road Basics

Introduction to raster roads

We are used to perceiving 3D effects within polygons whose vertices are suspended in three-dimensional space. However, old computers were not powerful enough to handle a lot of three-dimensional computing. Therefore, most often in old games used raster effects. These are special effects created by changing a variable line by line. This is well suited for older graphics hardware that had hardware scrolling acceleration and indexed color mode.

The raster effect of the pseudo-road was actually created in much the same way as the perspective effect in Street Fighter II, where the static image was deformed to add the illusion of three-dimensionality. Here is how it was implemented:

Most raster roads begin with a flat road image. In essence, this is a graphic depiction of two parallel lines on the earth extending into the distance. At a distance, these lines seem to the observer to be connected. This is the basic rule of perspective. In addition, to create the illusion of movement, most arcade racing games had lanes drawn on the road. The movement of these lanes on the road was achieved either by cyclically switching colors or changing the palette of each line. Curves and turns were performed by independent scrolling of each line, as in Street Fighter II.

We will look at curves and turns in the next section. In the meantime, let's concentrate on scrolling the road forward.

The simplest road

Take the image of the road described above: two parallel lines indicating the right and left sides of the road, extending into the distance. Moving away from the observer, they are getting closer. Here is an example of how this might look:



This image lacks road markings that create a good sense of perspective. For this effect in games, in addition to other road markings, alternating dark and light stripes are used. To add them, let's define a texture position variable. This variable is zero at the bottom of the screen and increases with each line up. When its value is below a certain number, the road is drawn in one shade. When the value is above this number, it is drawn in a different shade. After exceeding the maximum value, the position variable is again equal to zero, creating a repeating pattern.

However, changing it for each row is not enough, because then you get only a few stripes of different colors, which do not decrease with the removal of the road. So, we need another variable, which will change by a given value. It needs to be added to another variable every line, and then added to the last change in the position of the texture.

Here is an example of how the Z value for each row changes when moving into the distance. After the variables, I wrote what needs to be added to get the values ​​for the next line. I named the values ​​DDZ (delta-delta-Z), DZ (delta-Z) and Z. DDZ remains constant, DZ changes linearly, and Z - along a curve. You can consider Z the coordinate of the position Z, DZ the speed of the position, and DDZ the acceleration of the position (change in acceleration). Note that the value “4” is chosen arbitrarily, because it is convenient for this example.

DDZ = 4 DZ = 0 Z = 0 : dz += 4, z += 4

DDZ = 4 DZ = 4 Z = 4 : dz += 4, z += 8

DDZ = 4 DZ = 8 Z = 12 : dz += 4, z += 12

DDZ = 4 DZ = 12 Z = 24 : dz += 4, z += 16

DDZ = 4 DZ = 16 Z = 40 : и т.д.

Note that DZ is changed first, and then used to change Z. This can be explained as follows: suppose we move through the texture at a speed of 4. This means that after the first line we read the texture at position 4. The next line will be at position 12. After it 24. Thus, the passage through the texture is faster and faster. Therefore, I call these variables “texture position” (the place of the texture that we read), “texture speed” (how quickly we go through the texture) and “texture acceleration” (how fast the texture speed changes).

We use a similar method for drawing curves and hills without too many calculations. Now, to create the illusion of movement of the texture, you just need to change the beginning of the position of the texture at the bottom of the screen for each frame.

You may notice a flaw in this trick: the scaling factor is inaccurate. This leads to a distortion, which I will call the “oatmeal effect”. This deformation effect was present in early pseudo-three-dimensional games, for example, in OutRun: objects, including stripes on the road, seemed to slow down when moving from the center of the screen to the outside.

This method of finding the Z value has another drawback: it is not easy to predict what the value will be at each distance, especially when using hills. We will find out a more complicated way, which I call the Z-map. This is a table that computes the distance Z for each screen raster line. But first, we need some more math ... A math

trip: a three-dimensional perspective projection

There are ways to get rid of the effect of oatmeal. However, their implementation requires knowledge of traditional three-dimensional mathematics. We need to find a way to translate 3D coordinates so that they can be positioned on a 2D surface.



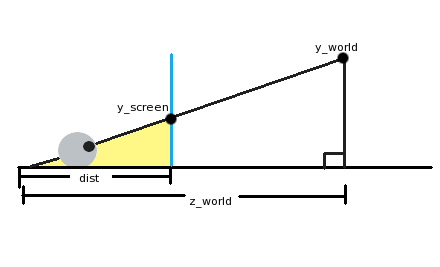
In the picture above, the eye (in the lower left corner) looks through the screen (blue vertical line) at an object in our three-dimensional world ("y_world"). The eye is at a distance of "dist" from the screen, and at a distance of "z_world" from the object. If you were engaged in geometry or trigonometry, you might notice that there are not one, but two triangles in the picture. The first triangle is a large one, from the eye to the surface on the right and up to the object that the eye is looking at. I painted the second triangle yellow. It is formed by the eye, a point on the screen in which we see the object, and the surface.

The hypotenuses of these two triangles (lines from the eye to the object) are at the same angle, although one is longer than the other. In essence, this is the same triangle, only scaled down. This means that the ratio of horizontal and vertical sides will be the same! In math notation:

y_screen/dist = y_world/z_world

Now we need to transform the equation to get y_screen. We get:

y_screen = (y_world*dist)/z_world

That is, to find the y coordinate of the object on the screen, we take the y coordinate of the world, multiply it by the distance from the eye to the screen, and then divide by the distance in the world. Of course, if we do this, then the center of view will be in the upper left corner of the screen! To verify this, simply substitute y_world = 0. To center, you need to add half the screen resolution to the result. The equation can be simplified a little if you imagine that the nose is pressed to the screen. In this case, dist = 1. The following equation is obtained:

y_screen = (y_world/z_world) + (y_resolution/2)

There is a relationship between the ratios and the viewing angle, as well as the scaling of the image so that it does not depend on the screen resolution. But to solve the problem with the road, we do not need it. If you're interested, look at the diagram in the top view: the angle to the edge of the screen is the area of ​​visibility, and the same connection remains.

More math: adding a scope to a three-dimensional projection

In fact, this is usually not necessary for most "road" engines. But this is useful so that the projection parameters are not dependent on resolution, or for objects that need to be rotated, or for integration with genuine 3D effects.

Let's get back to the original projection formula. The “dist” value from the equations above will be called “scaling”:

y_screen = (y_world*scaling)/z_world + (y_resolution/2)

The idea is that we need to scale all the points on the screen by a certain amount, which will allow the visible points to remain within the field of view (field-of-view, FOV). For the x-axis FOV and the y-axis FOV, two constants will be needed.

For example, suppose we work at 640x480 and want the FOV to be 60 degrees. We saw a three-dimensional projection diagram in side view. For this case, let's look at the diagram of the projected space in the top view: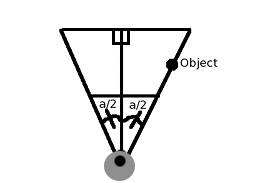


One way to solve the problem is to accept that if the object is on the right side of our FOV, it should be displayed on the screen at x = 640 (because the screen resolution is 640x480). If you look at the diagram, you can see that the FOV can be divided into two right-angled triangles, in which the angle of each is fov_angle / 2 (a / 2). And since our FOV is a cone, the object located on the right edge of the FOV, i.e. x = R * sin (a / 2) and
z = R * cos (a / 2), where R is any value of the radius. We can, for example, take R = 1. And we need the object to be displayed on the screen at x_screen = 640. We get the following (taking into account the basic projection formula): We replaced a / 2 with 30 (half from 60 degrees), designated sin / cos = tan, and voila! You can verify this by placing the object at the right end of the scope, substituting these values ​​in the original projection equation and making sure that X takes the value 640. For example, the point (x, z) with coordinates (20, 34.64) will be at X = 640, therefore that 20 is 40 * sin (30), and 34.64 is 40 * cos (30). It should be noted that the FOV values ​​for the horizontal (x) and vertical (y) axes will be different for the standard and widescreen monitors in the horizontal position. More Accurate Road: Using a Z-Card

x_screen=640 fov_angle=60 y_world=sin(60/2) z_world=(60/2) x_resolution/2=320 scaling=?

x_screen = (y_world*scaling)/z_world + (x_resolution/2)

640 = (sin(30)*scaling/cos(30)) + 320

320 = tan(30)*scaling

320/tan(30) = scaling

В общем случае: scaling = (x_resolution/2) / tan(fov_angle/2)







To solve the prospective problem, we need to create a pre-computed list of distances for each line of the screen. In short, the problem is to describe the plane in 3D.

To understand how this works, first imagine a two-dimensional analogue: a line! To describe a horizontal line in 2D, we can say that for each coordinate pair (x, y), the y coordinate will be the same.

If we bring it into three-dimensional space, the line will become a plane: for each distance x and z, the y coordinate will remain the same! If we consider a flat horizontal surface, it does not matter how far the camera is located, y will be constant. It also doesn’t matter how far the point is to the left or right, the y value will always be the same.

Let us return to finding out the distance to each of the lines of the screen: we will call our list a Z-card. The question of calculating the Z-card is to convert the three-dimensional projection formula to find the Z value for each screen Y!

First, take the equation from the previous section:

Y_screen = (Y_world / Z) + (y_resolution / 2)

Since we have Y_screen (each line), we transform the equation to find Z:

Z = Y_world / (Y_screen - (height_screen / 2))

Y_world as a whole is the difference between the ground level and the height of the camera, which will be negative. It is the same for each line, because, as stated in the introductory paragraph, we are still interested in a flat road. Besides the fact that the road will look more clearly and avoid the “oatmeal effect”, there is one more advantage: simplicity of calculating the maximum rendering distance.

The road is located on the screen by reading this buffer: for each distance, you need to find out what part of the road texture belongs to it, noting how many units each line or pixel of the texture occupies.

Although we know the distance for each row of the screen, it may be useful to cache for each line either the width of the road or the zoom factor. The scaling factor is opposite to the distance selected so that the value on the line in which the graphic image of the player’s car is located the most is equal to 1. It can be used to scale sprites on a given line or to determine the width of the road.

Curves and turns

Create bends.

To make the road curve, you just need to change the position of the center line in the shape of the curve. You can use a couple of ways to do this. One way is the same way that the Z positions were created in the “Simplest Way” section: using three variables. That is, starting from the bottom of the screen, the value by which the center of the road shifts to the left or right of each line increases steadily. As with texture reading, we can consider these variables as the position of the center line (curve), the speed of the curve, and the acceleration of the curve.

However, this method has problems. One of them is that it is not very convenient to create S-shaped curves. Another limitation: the entrance to the turn looks exactly the same as the exit of it: the road bends, and then simply bends.

To improve the situation, we can introduce the concept of road segments. The road segment is the part invisible to the player. You can consider it an invisible horizontal separator, establishing the curvature of the road above this line. At any given time, one of these segmented dividers is at the bottom of the screen, and the other goes down at a constant pace to the very bottom. Let's call the bottom segment basic because it defines the initial curvature of the road. Here's how it works:

When we start to draw the road, we start by looking at the base point and set the rendering options accordingly. As the turn approaches, its line of the segment is at a distance and approaches the player almost like any other road object, except that it should go down the screen at a constant pace. That is, at the specific speed at which the player moves, the segment splitter drops down the screen by the same number of lines per frame. Or, if using a Z-card, the same number of z-card elements per frame. If the segment “accelerated” towards the player, as 3d objects do on the track, the road would curve too sharply.

Let's see how it works. Suppose the segment line for the left curve is halfway down, and the base segment is just a straight road. When drawing a road, it will not begin to bend until it encounters a segment of the “left curve”. Then the road curve begins to change at the pace indicated by this point. When a moving segment reaches the bottom of the screen, it becomes a new base segment, and the previous base segment rises to the top of the road.

Two roads are shown below: one straight line, followed by a left turn, and the other with a bend to the left, followed by a straight line. In both of these cases, the position of the segment is halfway down the Z-card (or halfway down the screen). In other words, the road begins to bend or become straight halfway down the road. In the first picture, the camera enters into a rotation, and in the second, it exits from it.



And here is the same technique and the same position of the segment applied to the S-curve:



The best way to track the position of a segment is to determine where it is on the Z-card. That is, do not attach the position of the segment to the position of Y on the screen, but attach it to the position on the Z-card. Thus, it will still begin on the horizon of the road, but working with the hills will become much more convenient. It should be noted that on a flat road without changing heights, these two methods of tracking the position of a segment are similar.

Let's illustrate the above code:

current_x = 160  // половина экрана шириной 320
dx = 0 // величина кривой, постоянная для сегмента
ddx = 0 // величина кривой, изменяется построчно
для каждой строки экрана, снизу вверх:
  если строка положения экранной Z-карты ниже segment.position:
    dx = bottom_segment.dx
  иначе если строка положения экранной Z -карты выше segment.position:
    dx = segment.dx
  конец "если"
  ddx += dx
  current_x += ddx
  this_line.x = current_x
конец "для"
// Перемещение сегментов
segment_y += constant * speed // Константа гарантирует, что сегмент не будет двигаться слишком быстро
если segment.position < 0 // 0 - ближайшее
  bottom_segment = segment
  segment.position = zmap.length - 1 // Отправить положение сегмента на самое дальнее расстояние
  segment.dx = GetNextDxFromTrack() // Получить новую величину кривой из данных трассы
конец "если"

One of the great advantages of implementing curves in this way is that if there is a curve followed by a straight road, then the player will be able to see the straight road when exiting the curve. Similarly, if the curve is followed by a curve in the other direction (or even a more curved curve in the same direction), then the player can see this next section of the route before it hits it.

For the illusion to be complete, you need to add horizon graphics. As the curve approaches, the horizon does not change (or moves slightly). Then, when the curve is completely drawn, it is assumed that the car is turning along it, and the horizon quickly scrolls in the opposite direction to the curve. When the curve straightens again, the background continues to scroll until the curve ends. If you use segments, then you can simply scroll (scroll) the horizon in accordance with the settings of the base segment.

General curve formula

Having studied the technique of curves, described in detail in the section "The simplest road", we can draw an interesting conclusion. This conclusion relates more to mathematics than to the material described above, and you can safely skip it if your graphics engine should not be independent of resolution or use the “3d-projected segments” technique discussed in the section on hills.

Considering the example of a curve using “Z” from the “Simplest Road” section, you can see that the z-position (or x-position) of a given string is the sum of an increasing series of numbers (for example, 1 + 2 + 3 + 4). Such a series is called an arithmetic series or arithmetic progression. If you use instead of 1 + 2 + 3 + 4, for example 2 + 4 + 6 + 8 or 2 * 1 + 2 * 2 + 2 * 3 + 2 * 4, you can get a sharper curve. "2" in this case is the variable segment.dx. It can also be factorized by getting 2 (1 + 2 + 3 + 4)! Now all you need to do is find a formula that describes 1 + 2 + ... + N, where N is the number of lines that make up the curve. It is known that the sum of the arithmetic progression is N (N + 1) / 2. Therefore, the formula can be written as s = A * [N (N + 1) / 2], where A is the sharpness of the curve, and s is the sum. This equation can also be converted to add a starting point, for example, the center of the road below the screen. If we denote it by “x”, then we get s = x + A * [N (N + 1) / 2].

Now we have a formula to describe the curve. We want to get the answer to the question “knowing the starting point x and N of the lines of the curve, what should A be so that the curve reaches at the end of the x-position equal to s?” Transforming the equation to find A, we get A = 2 (s - x) / [n (n + 1)]. This means that the sharpness of a given curve can be stored relative to position X, which makes the graphics engine independent of resolution.

Perspective twists

It is much less interesting when only the car’s sprite moves during turns in the game. Therefore, instead of moving the sprite of the player’s car, we leave it in the center of the screen and move the road, and more importantly, move the position of the center line in the front (i.e. bottom) part of the screen. Now we assume that the player will always look at the road, so we will make the road end in the center of the screen. This will require a variable angle of the road. Therefore, we calculate the difference between the center of the screen and the position of the front of the road, and then divide by the height of the road graphics. This will give us a value for moving the center of the road on each line.

Sprites and data

Location of objects and scaling

Sprites need to be drawn from back to front. Sometimes this method is called the artist’s algorithm . To do this, you need to determine in advance where on the screen each object should be drawn, and then draw the objects at different stages.

This is done in the following way: when we go along the Z-map when drawing a road, we must also mark which line of the screen each sprite should be associated with. If the sprites were sorted by Z, this is trivial: every time you read the new value of the Z-card, you need to check whether the Z position of the next sprite is closer to the camera than the current value of the Z-card, or whether they are equal. If so, then mark the screen position Y of the sprite as belonging to the current line. Then check the next sprite in the same way. Continue this process until we get a sprite from the list whose position in Z is farther than the current one.

Position X of the facility must be monitored relative to the center of the road. Then the simplest way to horizontally position the sprite is to multiply the value by the scale factor of the current row (the inverse of Z) and add the result to the center of the road.

Storing track data

When I did my first demo with the road, I stored level information in a list of events that should occur at certain distances. Of course, distances were indicated in units of texture position. The events consisted of teams starting and ending curves. As far as I remember, the speed with which the road begins and ends to bend is arbitrary. The only rule is that it must match the speed of the player’s car.

However, if you use a system with segmentation, you can simply use the list of commands. The distance each team takes is similar to the speed at which an invisible segment moves to the bottom of the screen. It also allows you to create a track format that works for a tile map that allows you to convey fairly realistic track geography. That is, each tile can be one segment. A sharp turn can turn the track 90 degrees, and a smoother - 45 degrees.

Texturing the road

Now you may want to use a real graphic texture on the road instead of the changing lines that we have created at the moment. You can use a couple of ways to do this. A cheap and easy way: prepare a couple of textures for the road (for the effect of alternating lines). When drawing each horizontal line of the road, you need to stretch the texture so that it matches the width of this line. Or, if stretching is not possible, you need to select a row of one of two full bitmaps of the road (the approach used by Outrunners).

If you want the road to look more accurate, make the Z for each line correspond to the line number of the graphic texture. And voila! One textured road!

However, if you only need stripes of changing colors, the answer is even simpler, especially when using a fixed point. For each Z, you need to make one of the bits represent the shade of the road (dark or light). Then just draw the appropriate road pattern from the flowers for this bit.

Hills

Variations of the hills

There seem to be an almost infinite number of ways to create hill effects. Hill effects can be created with a wide range of geometric accuracy, with some less accurate techniques creating more convincing results. We will consider two possible ways.

Fake hills

After many experiments, I came to a flexible method of simulating hills, which uses few calculations. In addition, it accurately tracks objects below the horizon. This is the effect of scaling and deformation, vertically stretching and compressing the road. To generate the curvature of the hill, it uses the same summation trick that was used to draw the curves.

Here's how to do it: firstly, the rendering cycle should start from the beginning of the Z-card (nearest) and stop when it reaches the end (the farthest). If we reduce the rendering position of each line by 1, then the road will be drawn flat. However, if you reduce the rendering position of each line by 2, doubling the lines in the aisle, the road will be drawn twice as high. And finally, by varying the decrement value of the drawing position of each line, you can draw a hill that starts as a plane and rises up. If the next rendering position is farther from the current rendering position by more than one line, then the current line of the Z-card is repeated until we get to it, creating a scaling effect.

Descent from the hills is done in a similar way: if the position of the rendering increases, but not decreases, then we will go below the last drawn line. Of course, lines below the horizon will not be visible on the screen. Only lines one or more pixels above the last line are drawn. However, we still need to track objects below the horizon. To do this, take into account the Y position of each sprite when traversing the Z-card. Creating a Z-card larger than necessary for a flat road may help. Thus, when the buffer is stretched, it will not become too pixelated.

Now we need to move the horizon so that the picture is convincing for the player. I like to use the background in the style of the game "Lotus": in it the horizon not only consists of the outlines of the sky, but also from the graphics of a distant land. When the hill rises (increasing visibility), the horizon should lower slightly relative to the top of the road. When the hill goes down and the camera "rests" on the hill (limiting the scope), the horizon should rise up.

Here's what the effect looks like for descending from a hill and climbing on it, of course, without a horizon graphic:



Pros

• Low calculation load: no multiplication or division required
• Tracked objects on the back of the hill
• It seems that the viewing angle follows the player driving through the hills

Minuses

• Exact 3D geometry impossible
• Fine tuning is required to create a convincing effect.

Summing up: further development of raster roads

These cumulative curve formulas can be flexibly used if you don't need crazy curves or huge hills. In many games using such tricks, the road will scroll so fast that even a small curve looks convincing.

However, to create a more impressive road, you may need to exaggerate the effect. You can use high ddx or ddy in any of these curve formulas, but dx or dy should not exceed reasonable values. YouTube user Foppygames has discovered yet another trick that creates steeper curves from these formulas with accumulation: for each line, multiply the value of dx or dy by the value of z! This makes the curve steeper at a distance than it is in the foreground, and creates a pretty convincing effect .

And the experiments do not end there. In fact, the best thing about these engines is that there are no “right” ways to implement them. Everything that creates curves and bends pleasant to the eye is welcome in every way! In my first road engine, I used a sinusoid search table to bend the road.

You can also use multiplication: to shift the road to the right, you can, for example, multiply the x position by 1.01 for each row. To shift to the left by the same amount you need to multiply by 0.99 or 1 / 1.01 (the reciprocal of 1.01). However, armed with the knowledge that many old processors did not have multiplication operations or were weak in it, I settled on the accumulation technique, because it uses only addition. It seemed to me a more “authentic” way of creating bends in the road.

In some games, for example, OutRun even uses a simple splines system (at least judging by the excellent port on C ++ Cannonball made on the basis of reverse engineering .

Here, by playing and experimenting, you can choose the most suitable technique for you!

... or continue reading to learn a tricky trick that mixes 3d polygons, which is almost as fast, even more convincing, and can be played on the same old raster equipment. Are you intrigued?

Real 3d projected segments

Comparison of 3d-projected segments and raster roads

Raster roads are beautiful, but they can be made even more impressive by using a simple way to render polygons. This rendering method can even pull the same weak raster equipment. However, it uses more computation.

This trick is known to have been used in games like Road Rash and Test Drive II: The Duel. Here is what it is: the track consists of polygonal segments. However, instead of moving in full 3d space, they only move relative to the camera. For curves, the road still leans to the left or right, almost the same as in raster roads: there is no actual rotation that would be present when cornering the curve in a fully polygonal slider.

Here is a brief explanation of the principle:

• Since curves and road angles are still simulated, costly rotation calculations will not be needed
• In essence, the road is a strip of quadrangles: each section of the road is connected to the next section. This means that we can calculate the visibility of part of the road only on the basis of its screen position Y relative to the previous neighbor.
• The relationship between these quadrangles never changes. That is, the angle actually never changes, so the quadrangles are always and automatically sorted by Z.

Simple 3d-road

First, we break the road into polygonal quadrangles. Each of them will be called a segment. Like a segment in a fully raster road, here each segment still has a curve value (ddx), and either a hill value (ddy), or a y position that determines its height. Of course, they can also have other attributes, for example, a change in surface graphics.

The figure below shows a segmented road made up of a small number of polygons. Therefore, we can easily see the boundaries between the segments and how they affect the curvature of the road:



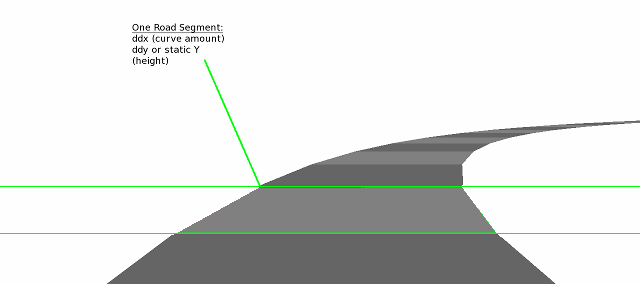
When rendering, the first thing we do is find the y position on the screen of each 3d segment using the screen_y = world_y / z formula. Or if the division is too slow, then you can find the height above the ground of a given segment by multiplying the segment height by the scaling factor for this row. Then it can be subtracted from the reverse z-map (this map is the answer to the question: what will be y for each z-position of a flat road?) To find the final position on the screen.

Then you need to linearly interpolate the width of the road and the texture (if required) between these heights. It is very simple to understand which 3d segments need to be drawn and which ones not: from the front to the back of the screen a three-dimensional segment will not be drawn, whose screen_y value is projected as less than the last drawn three-dimensional segment (however, its sprites can still be visible because they are issued - do not forget about it).

Scrolling road

Now we need to learn how to scroll through these segments, move the entire volume of polygons moving towards the camera. When the closest polygon of the segment passes through the camera, you need to move the whole way back to the starting point so that it closes. This is similar to how you can implement scrolling of a two-dimensional tile field by scrolling up one tile, and when it is reached, all the tiles are shifted and the new data of the tile map is loaded. Here we scroll up one segment, and when we reach it, we move the road back and load new road data.

But there is another very important detail: let's say the road has a sharp curve. You may have noticed that as you bend around this polygonal curve, it fluctuates at the moment you cross the segment boundary and the road then resets. This happens for an obvious reason: when passing through a curved segment, the center of the camera is associated with changes in the road. That is, by the time we reach the end of this segment, the road will no longer be centered. It looks as if we are traveling on the road at an angle. You may be tempted to fix this by moving the road to the center by simply interpolating the x positions of the objects.

However this is not trueand does not solve the problem completely: if the road is curved in a straight line, then everything will be fine. The problem is that the road bends, so the polygons are not lined up at a distance! In other words, we approximate the curve using polygonal segments. We want the curve to be more or less constant even when scrolling.

Jake at codeincomplete.com has a great solution to this problem. Instead of changing the x position of the road when moving along a segment, it’s worth changing the initial value dx from 0 to something that keeps the road in the center when moving along a segment. To do this, use the following formula: The

dx = -percentage_of_segment_traversed * ddx

percentage of a segment can be in the range from 0 to 1.0 and returns to its original value when the camera intersects the segments.

From the point of view of mathematics, this makes X roads a function of its Z. In other words, we maintain the same curve shape, regardless of how the points approximating it scroll. The very front segment is “dragged into place” with the rest of the road, which means that the subsequent X position of the segments is positioned correctly. You will clearly notice this if you test the way with a road from several polygons. This solves the following problems when passing a segment (assuming that the shape of the curve does not change):

• The center of the road (position x) remains constant
• dx is adjusted so that the next segment starts at the correct x position, regardless of the scrolling position of the road

The video illustrates this technique. I used a small number of segments and a very sharp curve to demonstrate the method. Note that when polygons move toward the player, they create the perfect curve shape. This is more obvious if you follow the right side of the road.


Placement of sprites

However, sprites on this three-dimensional segment should still be displayed and properly trimmed - if you accept that you are doing your own renderer and not using the Z-buffer. In fact, you can draw sprites at the last stage: if the sprite is on a fully visible segment, you don’t need to crop it, because it comes directly from the ground, which is our only polygon.

But if the sprite is on a segment that is not visible or partially visible, then we can easily crop it. First, find the top of the sprite. Then each line of the sprite will be drawn until it encounters the last visible screen position of the Y segment. That is, if there is a segment behind the sprite that should cover part of it, then we stop drawing the sprite when we get to this line. And if the top of the sprite is below the Y position of the last segment, then the sprite will be completely invisible and you can skip it.

Variations and rendering technologies

After we introduced the term polygons, you may be tempted to believe that polygon rendering procedures are needed to work with them. Technologies such as OpenGL or a simple trapezoid drawing procedure will do just fine with this. But even tile and sprite two-dimensional equipment will be quite enough for this.

Note that each beginning and each end of a road segment is perfectly horizontal. This means that they always begin and end on the same scan line. In much the same way that a fully pseudo-three-dimensional road is rendered on tile equipment by scrolling flat-road graphics, this technique can be repeated for three-dimensional segments. For more information, see the section “Special equipment for roads”. Although it discusses arcade machine equipment originally designed for rendering road effects, the same technique can be recreated in simple two-dimensional sprite systems using vertical scrolling of road graphics along with horizontal.

Additional reading on 3D projected segments

Since my demonstration of this variation is not yet ready, I recommend that you study the awesome Code inComplete tutorial if you are interested in the details of this technique.

pros

• For hills, you can use real three-dimensional geometry, which significantly increases the number of possible details
• A more holistic system: changes in the width of the earth and the road do not need to be performed in different techniques

Minuses

• Need more computing
• You need to use a decent number of segments, otherwise the road will look warped and polygonal.

Improvement

Multiple Roads

Most arcade racing games handle many roads simultaneously. Although the most obvious reason for this is the presence of several roads on the screen at the same time, but in this way other effects can be achieved. For example, OutRun uses several roads to create a six-lane highway. This allows the game to easily expand and narrow the road, as well as create convenient forks. In this case, two roads overlap each other and one of them is given the priority of rendering. Here is the famous OutRun start with two roads and without them (look at the right side of the bushes):



And, more importantly, below is an example of a highway on which two roads are laid to create six lanes, with and without a second road:

Similar effects

Endless “chessboard” The

endless “chessboard” in the space Harrier arcade game is a simple variation of the technique of creating roads. As in the case of roads, the game contains graphics of lines approaching the player in a perspective projection. In fact, the Space Harrier uses the same hardware as the Hang-On.

The figures below show the effect of the “checkerboard” of Space Harrier with palette changes and without changes. To turn it into a chessboard, you just need to change the color palette every few lines. This is similar to light and dark stripes on the road.



But how do you scroll left and right? It’s just a variation of the turns in a perspective style: when the player shifts left or right, the graphics of the earth are skewed. After a few pixels scroll, the earth "resets" or "collapses" its position. Therefore, it seems that it scrolls left or right unlimitedly.

Case Studies

Special equipment for roads

Despite the fact that there are many ways to render roads, it is interesting that many arcade games used equipment designed specifically for this purpose. These chips automated the principles of road rendering, but not the road calculations themselves. A typical example is Sega’s “road” OutRun chip, used in games such as Super Hang-on, Outrun, and Space Harrier.

Firstly, the chip had its own graphics memory. This road ROM practically kept a perspective view of the road, flat, centered and without curvature. The programmer approximately indicated for each line of the screen that line of perspective graphics that needs to be drawn. Each line also had an X offset (for curving the road) and each line had a different color palette (for drawing road markings and simulating movement). To demonstrate the example, here are some images of road graphics from the Sega racing game along with the road that was displayed in the game (I express special thanks to Charles MacDonald for his application for viewing roads):













The first thing you might notice is that the road graphics have a much higher resolution than the game graphics. In these examples, the road has a resolution of up to 512x256, and the resolution of the game display is only 320x224. This gives the graphics engine sufficient graphics to reduce the amount of distortion. You can also notice that the perspective of the road stored in the ROM is completely different from the perspective displayed in the game. It happened because the graphics in the ROM store only how the road can look at different widths of the road. Choosing the right lines for each screen line from a large graphic image is the task of the program.

The equipment supports two roads simultaneously, so you can prioritize the left or right road. This is necessary for those parts of the game in which the road forks, or when the central divider is between lanes.

If you are hacking ROMs, you can study examples of “road” chips in the MAME src / mame / video / segaic16.c and src / mame / video / taitoic.c files. Note that the Sega road graphics are stored in a two-bit planar format, and the center of the graphics can have a fourth color (the yellow line shown in the figures above).

Enduro

Enduro is a noteworthy game. It was released in 1983 for the incredibly weak game console of the 70s. But she still manages to create a convincing road effect, complemented by changes in weather and a change of day and night. In addition, this game is exciting even today!


Screenshot Enduro

As we can see, Enduro is slightly different from the road engines we reviewed. It immediately becomes apparent that the road is drawn only in contours: the earth on the sides of the road is not drawn in a different color. There are also no obstacles along the sidelines. If you play Enduro, you may notice that the road does not move in perspective. Instead, the player’s machine sprite and road shift left and right, creating the illusion of turns.

To better understand why Enduro looks like this, let's look at the limitations of the Atari 2600. The Atari 2600 console was designed for Combat (tank game) and Pong games. Therefore, it could display only two sprites, two squares representing the shells of each of the players, a square representing a ball, and a low-resolution background. And it's all.

But what is remarkable about Atari video equipment is that it is essentially one-dimensional: the program itself must update the graphics for each scan line. For example, to draw a sprite, the programmer needed to load a new line of graphics to display at the beginning of each line of the scan. To draw the ball object, the programmer needed to turn on the ball when the TV beam was on the desired line, and turn off the ball when the beam approached the line on which the ball was no longer visible.

This led to an important side effect: a solid vertical line could be drawn down the screen, turning on the ball or the projectile, and then not turning them off! If the programmer shifted these objects on each line, then it was possible to draw diagonal lines.

Now back to our topic. You can draw the road using background blocks, but the resolution is too low to be effective. Therefore, Atari racing games used two graphical objects of a projectile or ball to draw the left and right sides of the road, much like they could be used to draw lines. Enduro, in particular, used the first player’s projectile sprite and the ball sprite to draw the left and right sides. Pole Position used both sprite shells to draw the sides of the road, and then used the ball sprite to draw a dashed line in the center.


Screenshots of Pole Position at 2600 for comparison

We did not discuss how objects moved line by line on the Atari 2600. The Atari graphics chip had a feature called HMOVE (horizontal move, horizontal shift). It allowed the programmer to very simply set the offset of each line for all objects. The programmer needed only to indicate how many pixels different objects need to move, then call HMOVE, and voila - they all moved according to the desired values!

In Enduro, this function was used to draw curves. In short, Enduro created a table in memory of how the HMOVE values ​​of the left and right sides change when rendering the screen. It took up almost half the available Atari 2600 memory. Since Atari was so small, this value was read only for every four lines. For the left and right sides of the road, two different tables were used.

When the road was straight, all the array values ​​for the right side of the road were 8. HMOVE uses only the upper 4 bits, so the value 8 loaded in HMOVE did not shift the side of the road. The bottom 4 bits were used as an approximate fixed-point form.

For example, here is what a curve looks like in memory as it approaches (the horizon is the end of the array):

08,08,08,08,08,08,0a,0a,0b,0c,0e,0d,0e,0e,0f,10,13,11,12,13,14,17,16,17

And the next frame:

08,08,09,09,0a,0a,0b,0b,0c,0d,0d,0e,0f,0f,10,11,12,12,13,14,15,16,17,18

Note that increasing values ​​of the curve gradually overwrite smaller values, shifting to the front of the screen to create the illusion that the curve is approaching the player. What does Enduro do with this data? Here is the part when used to record the curve for the right side of the road.

For each line of the road sweep:

LDA $be      ; Загрузка данных из адреса $be
AND #$0f     ; Отсечение верхних 4 бит (эти биты использует HMOVE)
ADC $e4,x    ; Прибавление значения из таблицы кривых (X - это насколько мы далеки от передней части экрана)
STA $be      ; Повторное сохранение значения (чтобы можно было загрузить его снова для следующей строки развёртки, как мы это делали выше)
STA HMBL     ; Также записываем его в регистр Horizontal Motion - Ball (горизонтального перемещения мяча)

What does this code do? So $ be is the counter for the increasing value of the curve. When it loads, the top 4 bits are discarded, leaving a range from 0 to 16 ($ 0-F). Then the curve table entry corresponding to this scan line is loaded and added. At the end, it is saved in the counter and loaded into the horizontal shift register for the ball object (right side of the road).

Thus we achieve several actions. Firstly, the sides of the road move every two lines only when the road is straight: if the array consists of only 8 and $ be on the first line contains 0, then the next line will contain 8 (the upper nibble is still 0). The line after it will contain $ 10. But when $ 10 is again loaded into register A on the next scan line, the upper nibble is discarded, again leaving 0! As a result, the counter alternately takes the values ​​of $ 10 and 8. Since the HMOVE values ​​use only the upper 4 bytes, the line is alternately shifted to 0 or 1 position.

Well, what if the whole array consists of nines, not eights? Here's what happens: on the first line of the scan, 9 is saved in the HMOVE register of the ball and written back to the counter. On the next line, 9 is added to the value from the table again, resulting in $ 12 (decimal number 18). This will move the ball 1 (the top 4 bits are 1). On the line after it, the upper nibble is discarded, leaving 2. Adding 9 from the table, we get $ B. Let's look at another scan line. The value B is loaded. There is no upper nibble. Adding 9, we get $ 14 (20).

The sequence described above is 09.12.0b, 14. It will cause the ball to move every second line to these 4 lines. But gradually, the lower nibble will become large enough for the procedure to shift the ball sprite two lines in the left column. The template will then collapse, but after a few more lines, the side of the road will again shift to two lines in the column. In essence, this is an example of simple and extremely fast fixed-point math.

There is another obstacle to the implementation of the road system on such weak equipment: positioning sprites. In more complex systems, sprites can be positioned horizontally on the road as a percentage of the width of the road. But this requires fixed or floating point multiplication, and these operations are performed very slowly on the 6502 processor. For comparison, Enduro has only three possible positions for machines, which saves computing resources.

Road rash

Both Road Rash and Road Rash on 3do have awesome graphics engines. The original version of the game for Genesis provided a sense of relatively accurate three-dimensionality on the Genesis 68000 processor with a frequency of 7.25 MHz, and also coped with scaling objects on the road in real time. The version for 3do was no less surprising, because it turned out to be a mixture of 3D and pseudo-3D techniques. They were expertly combined, giving the player an amazing sense of speed.

As I mentioned above, Road Rash and Road Rash engines for 3do were a mix of 3D tricks and pseudo-3D. They used a technique similar to that described in the section “Real 3d-projected segments”: the hills are in 3D-space, but the curves of the road are not. Road Rash curves use the same method described in this article, and each road segment has its own DDX or “acceleration in x” value. Each segment also has a height relative to the height of the last segment. There are 50 segments on the screen at the same time.

But Road Rash for 3do is really interesting in that programmers have added coagulation to enhance the sense of speed: objects distant from the camera move slower and objects near the camera faster.

Road Rash for 3do also added polygon features on the sidelines, whose X-coordinates are still relative to the road. They are used to create hills, buildings and other complex elements. This takes a large amount of data, so the geometry and textures are loaded from disk during the passage of the route.

STUN Runner: Arcade machines against Lynx

STUN Runner at the time of release on arcade machines in 1989 was an amazing game. It used the technology of fully three-dimensional polygons with filling. She invited the player to take control of a futuristic race car flying along winding corridors at breakneck speed.

A little later I saw a version for Atari Lynx. The Atari Lynx console was a portable system released around the same time as the original Game Boy. Like the Game Boy, it has an 8-bit processor at 4 MHz. So the port was terrible, right? Well, watch the video yourself:


In fact, the port was fantastic! He became almost perfect and grabbed everything that made the arcade game so amazing. And this is on the portable equipment of the Game Boy era. How did they succeed?

It turned out that Lynx had an important weapon in its arsenal: hardware scaling. But this did not help much when rendering polygon graphics. It turns out that not only Lynx had aces up their sleeve: the port author also came up with his tricks.

To recreate the speed of the arcade machine, the Lynx version of STUN Runner returned to the pseudo-3D engine. The pieces of the polygons that make up the walls are actually sprites. In essence, these are objects on the side of the road that are glued to the road, much like the objects on the side of the road in any other pseudo-three-dimensional racing game. They are drawn using the artist's algorithm (back to front). This creates a convincing illusion of polygonal graphics and allows you to take advantage of the strengths of the equipment. And to save space in the cartridge, one sprite did not make up the full ring of the tunnel graphics. This not only saves space on the absence of empty, transparent pixels, but also allows you to use the horizontal reflection function of graphic equipment.

Another interesting problem that the port author had to solve was the branching of the tunnel. You can see it in the video above. The forked tunnel is actually a large sprite, the scale of which increases as you approach the player. After the player chooses a new path, the fork graphic disappears. According to the author, sometimes you can notice how the transport flies right through this sprite!

If you are interested in learning more about this, read the interview with the author of the original at AtariAge .

Roads on Commodore 64

This information belongs to Simon Nicol , who has found excellent vehicles for fast roads on the C64.

To begin with, a small introduction: on many console systems, pseudo-three-dimensional roads were created by drawing a straight road with tiles and line-by-line scrolling to create the appearance of curvature. However, for a game with a normal frame rate per second, this method was too fast on the Commodore 64.

Simon's engine instead uses the C64 bitmap mode and fast fill algorithm. Its quick fill algorithm uses self-modifying code to speed up rendering: each line is a sequence of pixel-by-pixel save operations indicating the address in the video memory. However, at the moment when the color should change, the code changes. The save command turns into a load command and the save address turns into a new color number.

The main advantage of this technique is that you can still use the sprite combining technique in it, which allows you to display more than eight sprites on the screen. According to Simon: “To shift the horizontal scrolling in order to get a stable raster effect, you need to manipulate the register $ D011. Otherwise, the raster IRQ at $ D012 will flicker terribly depending on the number of sprites in a particular raster line. For a smooth display, it is necessary to provide the necessary synchronism in the processor, or not to use the screen graphics and just change the border color. It will be continuous and without flickering, but the road will not appear on the screen, because it will have to be turned off. Such smooth line-by-line border color changes were used to sweep the raster down the screen, and they can be used to pause there, where you want to display the top of the screen. This technique was called hold-off $ D011 or sometimes FLD (flexible line distancing) (it was used to get rid of bad lines on Commodore VIC).

Other

Power Drift engines Power Drift is



interesting in that it is one of the few games I know that used sprite-based 3D. Each fragment of the track is a small piece of sprite, and the Sega flyby created by the camera demonstrated this. I have no evidence, but I think that games like F1 Exhaust Heat and RadMobile used a similar system. It is also worth noting that the booth with the Power Drift machine could tilt almost 45 degrees, so it was important to fasten it with a belt. Screenshots taken from system16.com.

Racin 'force



Racin 'Force reverse engineering was performed by Chals MacDonald. Racin 'Force runs on a Konami GX circuit board, which has a daughterboard with voxel engine features. This equipment is based on old equipment that could draw only floor cards in the mode 7 style of the SNES console. Its capabilities were expanded and allowed to create a height map using smart technology: it projects on a flat 3D surface not only a tile map, but also height information for each pixel on its own separate 3D plane. Then, for each screen pixel, it searches for elevation information on the projected elevation map and extrudes each pixel up if necessary. Screenshots taken from system16.com.

Further research

Here are some interesting sites that can be useful for a deeper study of pseudo-three-dimensional roads:

• Cannonball: Open source OutRun port
• Code inComplete JavaScript Racer

The code

Formulas and Tips

3D Projection

y_screen = (y_world*scale / z) + (screen_height >> 1)

or:

z = (y_world*scale) / (y_screen - (screen_height >> 1))

This formula gets the world x or y coordinates of the object, z of the object, and returns the x or y coordinate of the pixel. Or, with known world and screen coordinates, returns the location along z.

The scale defines the field-of-view (FOV) and can be found as follows:

scale_x = x_resolution/tan(x_angle/2)
scale_y = y_resolution/tan(y_angle/2)

Fast linear interpolation

o(x) = y1 + ((d * (y2-y1)) >> 16)

It is assumed here that all numbers are represented as 16.16 with a fixed point. y1 and y2 are two values ​​between which to interpolate, and d is a 16-bit fractional distance between two points. For example, if d = $ 7fff, then this will be the middle between two values. This is useful for determining where a value is between two segments.

Fixed point arithmetic

Floating-point operations are very expensive on older systems that do not have specialized mathematical devices. Instead, a fixed-point system is used. In it, under the fractional part of the number, a certain number of bits is allocated. For the test, let's assume that we assigned only one bit to the fractional part and left the remaining seven bits to the integer part of the number. This bit of the fractional part will represent half (because half plus half is equal to the whole). To get the integer value of the number stored in this byte, the number is shifted one position to the right. This method can be expanded and use any number of bits for the fractional and integer parts of the number.

Fixed-point multiplication is trickier than addition. In this operation, two numbers are multiplied, and then shifted to the right by the number of bits allocated to fractional parts. Due to overflow, an offset may sometimes be needed before multiplication, and not after. See the example of fixed point multiplication in the section “Fast linear interpolation”.

Point rotation

x' = x*cos(a) - y*sin(a)
y' = x*sin(a) + y*cos(a)

Here is a simple point rotation formula. In the article, I briefly mentioned it as a very expensive operation. As you can see, it uses at least two table searches, four multiplication operations and two additions, but the sine and cosine values ​​can be reused for each point. Rotation for hills means rotation in the Z and Y coordinates, and not in the X and Y coordinates. For the derivation of this formula, see the Rotation of axes section .

Rid of division

Instead of dividing the object by the z coordinate in standard projection formulas, you can use the properties of the road to speed up the calculations. Suppose we have the z and y positions of a 3D segment, and we need to find which line of the screen it matches. First we read the z-card until we get to the z-position of the 3D segment. Then we multiply the segment height by the corresponding scaling value. The result will be the number of pixels above the road to which the segment belongs.

Using Z as a Scale Value

Scaling procedures consist in increasing or decreasing the reading speed by the graphic data rendering procedure. For example, if you set the half reading speed, the sprite will have a size twice as large. This happens because with each pixel rendering, the reading position of the sprite data increases by only half, which leads to an increase in the reading position by an integer for only every two pixels.

Typically, the scaling procedure has parameters such as x, y, and the scaling factor. But since the coefficient is 1 / z, you can reuse the Z value of this sprite! However, we still need a scaling factor to determine the boundaries of the sprite in order to center it when scaling.

Glossary

Bad line- in the C64 VIC II graphics chip, on the first pixel of each background tile, the VIC replaces the processor to insert more data, such as color. Since there are fewer cycles left for the program to compute, this is called bad lines.

Elevation map - an array of elevation values. In a polygonal or voxel landscape engine, this can be a two-dimensional array (imagine the landscape in top view). However, in a road engine, a height map is enough to be one-dimensional (imagine the landscape in side view).

Indexed Color Mode- In older systems with few colors on the screen, indexed color modes were usually used. One of the most popular indexed color modes is the 256-color VGA modes. In these modes, each pixel was represented by a byte. Each byte stored an index value from 0 to 255. When rendering the screen, the index number for each pixel was in the palette. Each entry in the palette could be one of 262,144 possible VGA colors. As a result, even though there could be only 256 colors on the screen at the same time, the user could select each color from a much larger palette.

Linear interpolation is the process of obtaining intermediate values ​​from a set of data by drawing lines between points.

Artist Algorithm- This is a way to draw overlapping objects from distant objects to close ones. It ensures that closer objects will always be on top of distant ones.

Planar graphics mode is a mode in which an N-bit image was composed of N single-bit images combined to produce the final image. It is the opposite of most graphics modes (sometimes called chunky ), in which an N-bit image is composed of N-bit pixel values.

The raster effect is a graphic trick that uses the nature of most computer (raster) displays based on scan lines.

Scaling factorIs the reciprocal of Z. The number by which you want to multiply the scale of the object at a given distance along the Z axis.

Segment (road) - I use the term segment to indicate the position in which the road behaves in one way below and the other in the above. For example, a segment may separate a left turn in the lower half of the screen from a right turn in the upper half. As the segment approaches the player, it seems that the road first bends to the left, and then to the right.

Three-dimensional segment (roads)- I use this term to refer to a horizontal line having both a distance along Z and a height along Y in world coordinates. Unlike a vertex, which can be a 3D point, a three-dimensional segment will be a 3D line, whose left and right end points along the X axis are plus and minus infinities.

Voxel is a three-dimensional pixel. Voxel landscape and ray tracing engines have become popular with Commanche: Maximum Overkill.

Z-map is a search table that links each line of the screen to a distance along Z.

Gallery

Below is a set of screenshots demonstrating different ways to create custom road engines.

Cisco Heat



The hills in this game are approaching like a solid wall. The turns also look very exaggerated. The engine seems to be quite flexible and handles several roads at the same time, and can also show the height of one road relative to another.

Pole Position



This is the first pseudo-three-dimensional game with smooth movement, which I remember. Today it is not very impressive graphically.

Hydra



Another shoot em up for Atari Roadblasters. It has a very beautiful jump effect, in which the perspective of the road layer is shifted, due to which the nearest objects disappear from the screen. In this game, objects at various distances to the earth are interestingly projected.

Outrunners



This sequel to Outrun is a great example of rollercoaster-like hills. Everything is quite exaggerated, resulting in an ultra-fast racing game, but with good handling.

Road rash



In the Road Rash version for the 32-bit generation of consoles, everything was textured, and buildings were smartly drawn next to the curb. Therefore, many had the impression that this is a fully polygonal game, quickly running on 3do. However, the way the objects bend around the edges, the coagulation of buildings and the fact that it was impossible to turn back, proves that this is not a completely polygonal game. The sharp lines on the road surface give a hint of a system of projected segments. The tracks are very detailed and varied. The 16-generation Road Rash is also made with high quality, it has a flexible engine with a small fraction of fake texturing (but it was slow).

Turbo



The predecessor of the Pole Position with hills and bridges. Are there any disadvantages? The game does not have transitions from hills to bridges and curves. For it, analog graphics scaling equipment was used.

Spy Hunter II



I don't know what the creators of Spy Hunter II were thinking. Good idea, poor execution. The effects of the road are very similar to Turbo, but the transitions are made a little better.

Pitstop II



This technique is so fast that even on a weak Commodore 64 you could play a split-screen racing game.

Enduro



Enduro demonstrates the use of pseudo-3D on the Atari 2600.

Enduro Racer



Not to be confused with Enduro: it was a three-dimensional likeness of Excitebike. The screenshot shows the technique of creating hills. The hills are quite sharp, flexible, but generally do not affect the position of the horizon, so I think that interpolated points were used.

Lotus



Lotus uses the technique of rather curved hills. Interestingly, Lotus drew the top of the road over the horizon, and then filled the gap with solid color to simulate the descent from the hill.

Test Drive II



I don’t know exactly how the test drive 2 graphics were created. Although it’s obvious that the race is not polygonal, it really tries to reproduce a lot of roads realistically. The game is similar to the Need for Speed ​​series, but has overtaken it by several years in terms of release time.

Speed ​​buggy



When cornering in this game, not only the perspective shifts, but the road slides a little to the left or right.