February 14, 2017 at 17:15

Create an InceptionV3 Neural Network for Image Recognition



Hello, Habr! Under the cut, we will talk about the implementation of a convolutional neural network of the InceptionV3 architecture using the Keras framework . I decided to write an article after reading the tutorial " Building powerful classification models using a small amount of data ." With the approval of the author of the tutorial, I slightly changed the content of my article. Unlike the neural network VGG16 proposed by the author , we will train the Google deep neural network Inception V3 , which is already pre-installed in Keras.

You will learn:

  1. Import the neural network Inception V3 from the Keras library;
  2. Set up the network: load weights, change the upper part of the model ( fc-layers ), thus adapting the model to binary classification;
  3. Fine-tune the lower convolutional layer of the neural network;
  4. Apply data augmentation using ImageDataGenerator;
  5. Train the network in parts to save resources and time;
  6. Evaluate the performance of the model.

When writing an article, I set myself the task of presenting the most practical material that will reveal some interesting features of the Keras framework.

Recently, tutorials devoted to the creation and application of neural networks are increasingly appearing. It is with great pleasure that I observe an interesting trend: new posts are becoming more and more understandable for non-specialists in the field of programming. Some authors even make attempts to introduce readers to this topic, using the most natural language. There are also excellent articles (e.g. 1 , 2 , 3 ) that combine a reasonable amount of theory and practice, which allows you to quickly understand the necessary minimum and start creating something of your own.

So, to the point!

First things first, a little about libraries:
I recommend installing the Anaconda platform . I used Python 2.7. For work it is convenient to use Jupyter notebook . It is already preinstalled on Anaconda. We will also need to install the Keras framework . As a backend, I used Theano . You can use Tensorflow , because Keras supports both of them. Installing CUDA for Theano on Windows is described here .

1. Data:


In our example, we will use images from a machine learning competition called " Dogs vs Cats " at kaggle.com . Data will be available after registration. The set includes 25,000 images: 12,500 cats and 12,500 dogs. Class 1 corresponds to dogs, class 0 to cats. After downloading the archives, place 1000 images of each class in directories as follows:

data/
    train/
        dogs/
            dog001.jpg
            dog002.jpg
            ...
        cats/
            cat001.jpg
            cat002.jpg
            ...
    validation/
        dogs/
            dog1000.jpg
            dog1001.jpg
            ...
        cats/
            cat1000.jpg
            cat1001.jpg
            ...

Nothing prevents you from using the entire data set. I, as well as the author of the original article, decided to use a limited selection to check the efficiency of the network with a small set of images.

We have three problems:


  1. Limited amount of data;
  2. Limited system resources (for example, I have Intel Core i5-4440 3.10GHz, 8 GB of RAM, NVIDIA GeForce GTX 745);
  3. Limited time: we want to train the model in less than a day.

With a limited image volume, there is a high probability of retraining . To combat this, you need:


  1. Install a big dropout. In our case, it will be 0.5;
  2. We will use data augmentation. This technique will allow us to increase the number of images through various transformations (in our case there will be changes in scale, shifts, horizontal reflection).
  3. For our experiment, we will take a deep network.

The last point should concern us, because a deep neural network is demanding on resources. I couldn’t even teach VGG16 on my video card, not to mention such a giant as Inception. However, the solution is:

  1. Initially, we use a model trained on a large number of images from the imagenet database . Fortunately, the set of images included cats and dogs;
  2. We will train the model in parts:
  3. First, run augmented images through the bottom of the network (only through Inception) and save them as numpy arrays;
  4. Using the resulting numpy arrays, train the upper fully connected layer;
  5. Then, we will combine the upper and lower layers of the model and fine-tune the new model, but at the same time we will block all layers except the last from learning from Inception.

The only solution to the problem over time, I still see the use of parallel computing. For this you need a graphics card with CUDA support . I hope that installing CUDA for Python will not cause you much trouble .

Import the libraries:

from keras.preprocessing.image import ImageDataGenerator
from keras.models import Sequential, Model
from keras.applications.inception_v3 import InceptionV3
from keras.callbacks import ModelCheckpoint
from keras.optimizers import SGD
from keras import backend as K
K.set_image_dim_ordering('th')
import numpy as np
import pandas as pd
import h5py
import matplotlib.pyplot as plt

2. Create the InceptionV3 model, load the images into it, save them:


Large picture with a diagram of our actions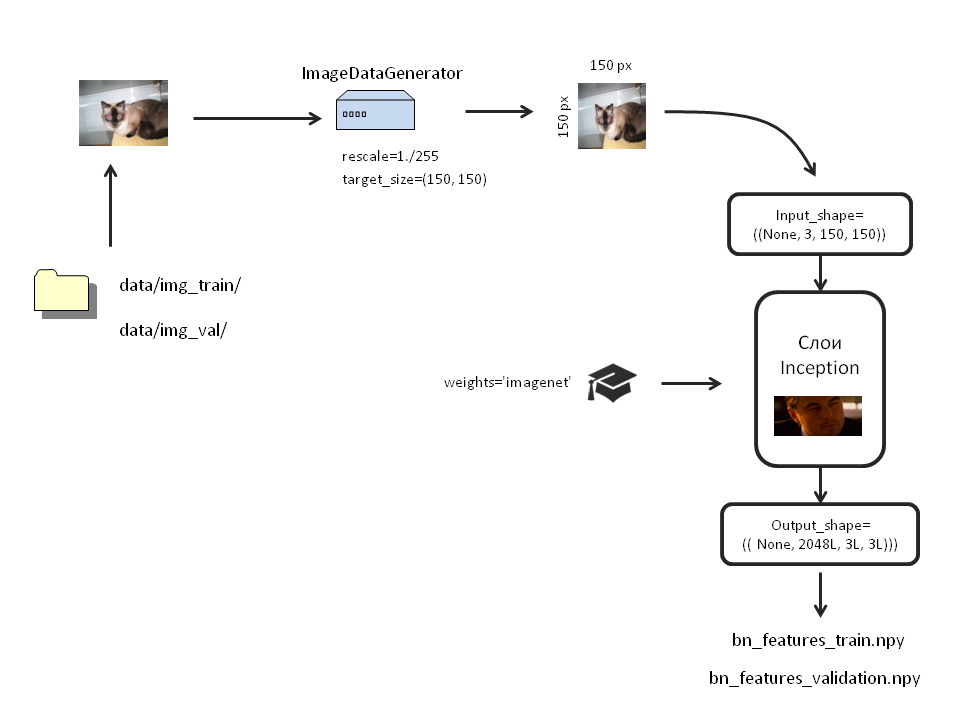


The Keras library houses several trained neural networks.

Model argument list
include_top: enable or disable the top of the network, which is a fully connected layer with 1000 outputs.
We do not need it, so we set: include_top = False;

weights : load / not load trained weights. If None, weights are initialized randomly. If “imagenet”, weights loaded on ImageNet data will be loaded .
In our model weights are needed, therefore weights = "imagenet";

input_tensor : this argument is convenient if we use the Input layer for our model.
We will not touch him.

input_shape: in this argument we set the size of our image. It is indicated if the top layer is detached (include_top = False). If we loaded the model with the top layer, one hundred image size should be only (3, 299, 299).
We have removed the top layer and want to analyze smaller images (3, 150, 150). Therefore, it seems: input_shape = ()

We create our model:


inc_model=InceptionV3(include_top=False, 
                      weights='imagenet', 
                      input_shape=((3, 150, 150)))

Now let's do the data augmentation. For this, Keras provides the so-called ImageDataGenerator. They will take images directly from folders and carry out all the necessary transformations on them.

Pictures of each class should be in separate folders. In order not to load the RAM with images, we transform them right before uploading them to the network. To do this, use the .flow_from_directory method. Let's create separate generators for training and test images:

bottleneck_datagen = ImageDataGenerator(rescale=1./255)  #собственно, генератор
train_generator = bottleneck_datagen.flow_from_directory('data/img_train/',
                                        target_size=(150, 150),
                                        batch_size=32,
                                        class_mode=None,
                                        shuffle=False)
validation_generator = bottleneck_datagen.flow_from_directory('data/img_val/',
                                                               target_size=(150, 150),
                                                               batch_size=32,
                                                               class_mode=None,
                                                               shuffle=False)

I want to highlight an important point. We specified shuffle = False . That is, images from different classes will not be mixed. First, images from the first folder will arrive, and when they all end, from the second. Why you need it, see later.

Run the augmented images through the trained Inception and save the output as numpy arrays:

bottleneck_features_train = inc_model.predict_generator(train_generator, 2000)
np.save(open('bottleneck_features/bn_features_train.npy', 'wb'), bottleneck_features_train)
bottleneck_features_validation = inc_model.predict_generator(validation_generator, 2000)
np.save(open('bottleneck_features/bn_features_validation.npy', 'wb'), bottleneck_features_validation)

The process will take some time.

3. Create the upper part of the model, load the data into it, save them:


Scheme


In the original post, the author used one network layer with 256 neurons, however I will use two layers of 64 neurons each and a Dropout layer with a value of 0.5. I was forced to make this change due to the fact that when I trained the finished model (which we will do in the next step), my computer crashed and rebooted.

Load the arrays:


train_data = np.load(open('bottleneck_features_and_weights/bn_features_train.npy', 'rb'))
train_labels = np.array([0] * 1000 + [1] * 1000) 
validation_data = np.load(open('bottleneck_features_and_weights/bn_features_validation.npy', 'rb'))
validation_labels = np.array([0] * 1000 + [1] * 1000)

Please note that we previously specified shuffle = False . And now we can easily specify labels . Since in each class we have 2000 images and all the images were received in turn, we will have 1000 zeros and 1000 units for the training and for the test samples.

Create a model of the FFN network, compile it:


fc_model = Sequential()
fc_model.add(Flatten(input_shape=train_data.shape[1:]))
fc_model.add(Dense(64, activation='relu', name='dense_one'))
fc_model.add(Dropout(0.5, name='dropout_one'))
fc_model.add(Dense(64, activation='relu', name='dense_two'))
fc_model.add(Dropout(0.5, name='dropout_two'))
fc_model.add(Dense(1, activation='sigmoid', name='output'))
fc_model.compile(optimizer='rmsprop', 
              loss='binary_crossentropy', 
              metrics=['accuracy'])

Load our arrays into it:


fc_model.fit(train_data, train_labels,
            nb_epoch=50, batch_size=32,
            validation_data=(validation_data, validation_labels))
fc_model.save_weights('bottleneck_features_and_weights/fc_inception_cats_dogs_250.hdf5') # сохраняем веса

Now we are not loading data from folders, so we use the usual fit method .

The learning process will be indecently fast. Each era took me 1 second:
Train on 2000 samples, validate on 2000 samples
Epoch 1/50
2000/2000 [==============================] - 1s - loss: 2.4588 - acc: 0.8025 - val_loss: 0.7950 - val_acc: 0.9375
Epoch 2/50
2000/2000 [==============================] - 1s - loss: 1.3332 - acc: 0.8870 - val_loss: 0.9330 - val_acc: 0.9160
…
Epoch 48/50
2000/2000 [==============================] - 1s - loss: 0.1096 - acc: 0.9880 - val_loss: 0.5496 - val_acc: 0.9595
Epoch 49/50
2000/2000 [==============================] - 1s - loss: 0.1100 - acc: 0.9875 - val_loss: 0.5600 - val_acc: 0.9560
Epoch 50/50
2000/2000 [==============================] - 1s - loss: 0.0850 - acc: 0.9895 - val_loss: 0.5674 - val_acc: 0.9565


Estimate the accuracy of the model:

fc_model.evaluate(validation_data, validation_labels)

[0.56735104312408047, 0.95650000000000002]

Our model satisfactorily copes with its task. But it only accepts numpy arrays. This does not suit us. In order to get a full-fledged model that accepts input images, we will connect our two models and train them again.

4. Create the final model, load the augmented data into it, save the weights:


Scheme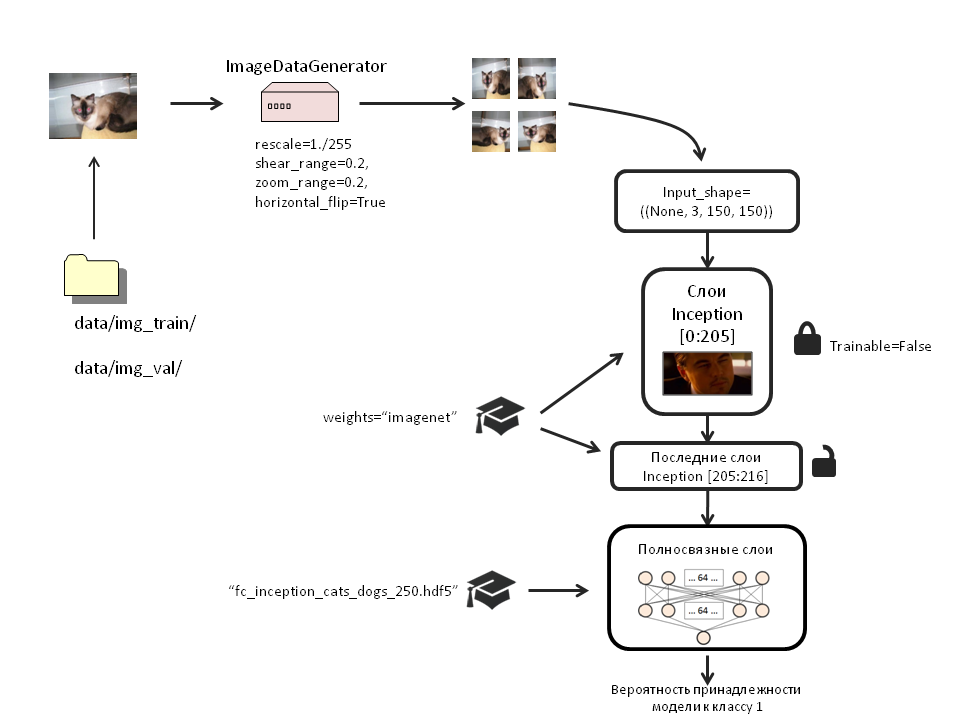


weights_filename='bottleneck_features_and_weights/fc_inception_cats_dogs_250.hdf5'
x = Flatten()(inc_model.output)
x = Dense(64, activation='relu', name='dense_one')(x)
x = Dropout(0.5, name='dropout_one')(x)
x = Dense(64, activation='relu', name='dense_two')(x)
x = Dropout(0.5, name='dropout_two')(x)
top_model=Dense(1, activation='sigmoid', name='output')(x)
model = Model(input=inc_model.input, output=top_model)

Load the weights in it:

weights_filename='bottleneck_features_and_weights/fc_inception_cats_dogs_250.hdf5'
model.load_weights(weights_filename, by_name=True)

Frankly, I did not notice any difference between the effectiveness of training a model with or without loading weights. But I left this section because it describes how to load weights into certain layers by name (by_name = True).

Lock inception layers 1 through 205:


for layer in inc_model.layers[:205]:
    layer.trainable = False

Compile the model:


model.compile(loss='binary_crossentropy',
              optimizer=SGD(lr=1e-4, momentum=0.9),
                #optimizer='rmsprop',
              metrics=['accuracy'])

Please note, when we first trained fully-connected layers from .npy arrays, we used the RMSprop optimizer . Now, to fine-tune the model, we use Stochastic gradient descent. This is done in order to prevent too pronounced updates to already trained scales.

We will make sure that only the weights with the greatest accuracy on the test sample are saved in the training process:

filepath="new_model_weights/weights-improvement-{epoch:02d}-{val_acc:.2f}.hdf5"
checkpoint = ModelCheckpoint(filepath, monitor='val_acc', verbose=1, save_best_only=True, mode='max')
callbacks_list = [checkpoint]

Create new image generators to train the complete model. We will transform only the training sample. We won’t touch the test.

train_datagen = ImageDataGenerator(
        rescale=1./255,
        shear_range=0.2,
        zoom_range=0.2,
        horizontal_flip=True)
test_datagen = ImageDataGenerator(rescale=1./255)
train_generator = train_datagen.flow_from_directory(
        'data/img_train/',
        target_size=(150, 150),
        batch_size=32,
        class_mode='binary')
validation_generator = test_datagen.flow_from_directory(
        'data/img_val/',
        target_size=(150, 150),
        batch_size=32,
        class_mode='binary')
pred_generator=test_datagen.flow_from_directory('data/img_val/',
                                                     target_size=(150,150),
                                                     batch_size=100,
                                                     class_mode='binary')

we use pred_generator later to demonstrate how the model works.

Upload images to the model:


model.fit_generator(
        train_generator,
        samples_per_epoch=2000,
        nb_epoch=200,
        validation_data=validation_generator,
        nb_val_samples=2000,
    callbacks=callbacks_list)

We hear the cooler noise and wait ...
Epoch 1/200
1984/2000 [============================>.] - ETA: 0s - loss: 1.0814 - acc: 0.5640Epoch 00000: val_acc improved from -inf to 0.71750, saving model to new_model_weights/weights-improvement-00-0.72.hdf5
2000/2000 [==============================] - 224s - loss: 1.0814 - acc: 0.5640 - val_loss: 0.6016 - val_acc: 0.7175
Epoch 2/200
1984/2000 [============================>.] - ETA: 0s - loss: 0.8523 - acc: 0.6240Epoch 00001: val_acc improved from 0.71750 to 0.77200, saving model to new_model_weights/weights-improvement-01-0.77.hdf5
2000/2000 [==============================] - 215s - loss: 0.8511 - acc: 0.6240 - val_loss: 0.5403 - val_acc: 0.7720
… 
Epoch 199/200
1968/2000 [============================>.] - ETA: 1s - loss: 0.1439 - acc: 0.9385Epoch 00008: val_acc improved from 0.90650 to 0.91500, saving model to new_model_weights/weights-improvement-08-0.92.hdf5
2000/2000 [==============================] - 207s - loss: 0.1438 - acc: 0.9385 - val_loss: 0.2786 - val_acc: 0.9150
Epoch 200/200
1968/2000 [============================>.] - ETA: 1s - loss: 0.1444 - acc: 0.9350Epoch 00009: val_acc did not improve
2000/2000 [==============================] - 206s - loss: 0.1438 - acc: 0.9355 - val_loss: 0.3898 - val_acc: 0.8940


It took me 210-220 seconds for each era. 200 eras of study took about 12 hours.

5. Estimate the accuracy of the model


model.evaluate_generator(pred_generator, val_samples=100)

[0.2364250123500824, 0.9100000262260437]

So pred_generator came in handy . Please note val_samples must match the value of batch_size in the generator!

Accuracy 91.7%. Given the limited sampling, I will take the liberty of saying that this is not bad accuracy.

Illustrate the model


Just looking at the% of correct answers and the magnitude of the error is not interesting to us. Let's see how many correct and incorrect answers the model gave for each class:

imgs,labels=pred_generator.next()
array_imgs=np.transpose(np.asarray([img_to_array(img) for img in imgs]),(0,2,1,3))
predictions=model.predict(imgs)
rounded_pred=np.asarray([round(i) for i in predictions])

pred_generator.next () is a convenient thing. It loads images into a variable and assigns labels.

The number of images of each class will be different for each generation:

pd.value_counts(labels)
0.0    51
1.0    49
dtype: int64

How many images of each class did the model predict correctly?

pd.crosstab (labels, rounded_pred)
Col_00.01.0
Row_0
0.0474
1.0841

For the model, 100 random images were uploaded: 51 images of cats and 49 dogs. Of the 51 cats, the model correctly recognized 47. Of the 50 dogs, 41 were correctly recognized. The overall accuracy of the model in this narrow sample was 88%.

Let's see which photos were not recognized correctly:


wrong=[im for im in zip(array_imgs, rounded_pred, labels, predictions) if im[1]!=im[2]]
plt.figure(figsize=(12,12))
for ind, val in enumerate(wrong[:100]):
    plt.subplots_adjust(left=0, right=1, bottom=0, top=1, wspace = 0.2, hspace = 0.2)
    plt.subplot(5,5,ind+1)
    im=val[0]
    plt.axis('off')
    plt.text(120, 0, round(val[3], 2), fontsize=11, color='red')
    plt.text(0, 0, val[2], fontsize=11, color='blue')
    plt.imshow(np.transpose(im,(2,1,0)))


Blue numbers are a true class of images. Red numbers are predicted by the model (if the red number is less than 0.5, the model believes that the cat in the photo, if more than 0.5, then the dog). The larger the number approaches zero, the more confident the network is that there is a cat in front of it. Interestingly, many dog ​​image errors contain small breeds or puppies.

Let's see the first 20 images that the model predicted correctly:


right=[im for im in zip(array_imgs, rounded_pred, labels, predictions) if im[1]==im[2]]
plt.figure(figsize=(12,12))
for ind, val in enumerate(right[:20]):
    plt.subplots_adjust(left=0, right=1, bottom=0, top=1, wspace = 0.2, hspace = 0.2)
    plt.subplot(5,5,ind+1)
    im=val[0]
    plt.axis('off')
    plt.text(120, 0, round(val[3], 2), fontsize=11, color='red')
    plt.text(0, 0, val[2], fontsize=11, color='blue')
    plt.imshow(np.transpose(im,(2,1,0)))


It can be seen that the model decently copes with the task of image recognition in relatively small samples.

I hope the post has been helpful to you. I will be happy to hear your questions or suggestions.

Github Project
Tags:

Also popular now: