March 23, 2017 at 09:21

How to evaluate the quality of the A / B testing system



    For more than six months now, the company has been using a single system for conducting A / B experiments. One of the most important parts of this system is the quality control procedure, which helps us understand how much we can trust the results of A / B tests. In this article, we will describe in detail the principle of the quality control procedure for those readers who want to test their A / B testing system. Therefore, the article has many technical details.

    A few words about A / B testing



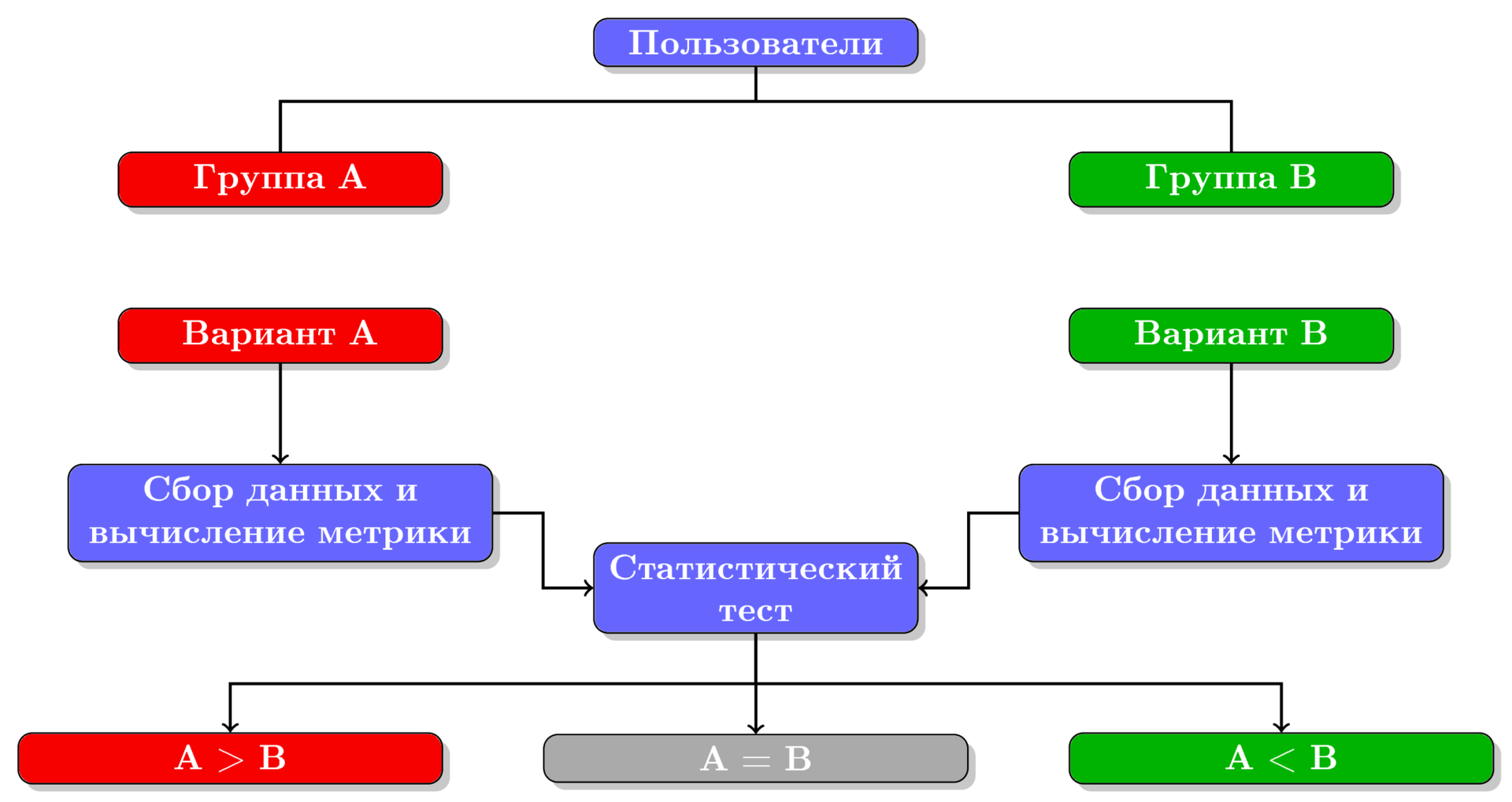
    Figure 1. A / B testing process flow chart.

    In general, the A / B testing process can be divided into the following steps (shown in the figure):

    1. The distribution of users in two groups A and B.
    2. Presenting two different options to two user groups.
    3. Data collection and calculation of metric values ​​for each group.
    4. Comparison using a statistical test of the metric values ​​in both groups and deciding which of the two options won.

    In principle, using A / B tests, you can compare any two options, but for definiteness, we will assume that group A is shown the current version working in production, and group B is shown the experimental version. Thus, group A is the control group, and group B is experimental. If users in group B are shown the same option as in group A (that is, there is no difference between options A and B), then such a test is called an A / A test.

    If one of the options won in the A / B test, then they say that the test has turned red.

    History of A / B testing in the company


    A / B testing at HeadHunter began, we can say spontaneously: development teams arbitrarily divided the audience into groups and conducted experiments. However, there was no common pool of verified metrics - each team calculated its own metrics from user actions logs. There was no general system for determining the winner either: if one option was much superior to the other, then it was recognized as the winner; if the difference between the two options was small, then statistical methods were used to determine the winner. The worst part was that different teams could experiment on the same user group, thereby influencing each other's results. It became clear that we needed a single system for conducting A / B tests.

    Such a system was created and launched in July 2016. Using this system, the company has already conducted 77 experiments. The number of A / B experiments by month is shown in Figure 2.


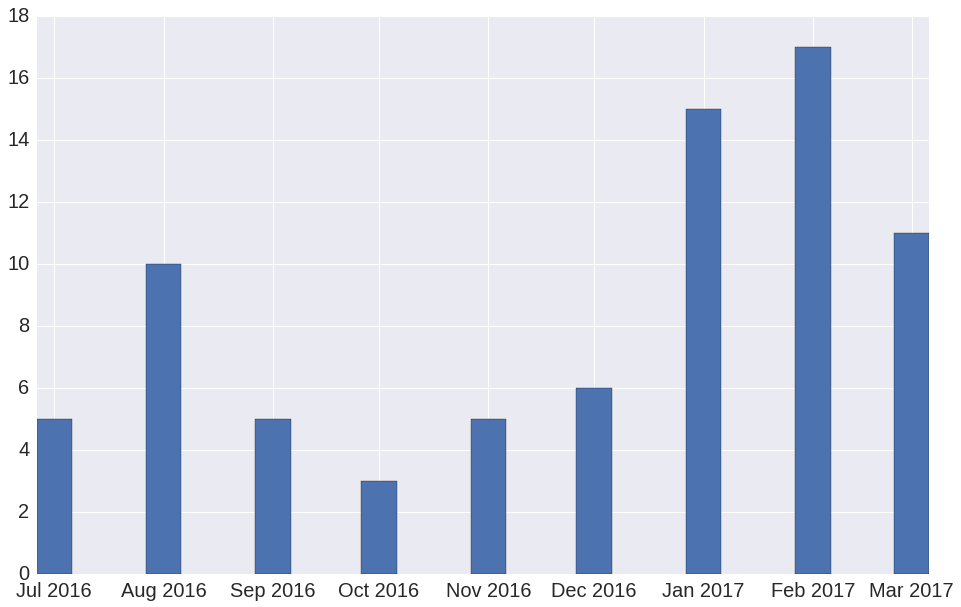
    Figure 2. The number of A / B experiments by months since the launch of the A / B testing system. The number of experiments for March 2017 is incomplete, because at the time of publication this month has not yet ended.

    When creating the A / B testing system, we paid most attention to the statistical test. First of all, we were interested in the answer to the following question:

    How to make sure that the statistical test does not deceive us and that we can trust its results?

    The question is not at all idle, since the harm from incorrect results is stat. test may be even more than the lack of results.

    Why we may have reasons not to trust the stat. test? The fact is that a statistical test involves a probabilistic interpretation of the measured values. For example, we believe that each user has a “probability” of committing a certain successful action (successful actions may be registration, purchase of goods, like, etc.). Moreover, we consider the actions of different users to be independent. But initially, we do not know how well user actions correspond to the probabilistic model of stat. test.

    In order to evaluate the quality of the A / B testing system, we conducted a large number of A / A tests and measured the percentage of tests that were stained, that is, the percentage of cases in which stat. the test was mistaken, claiming a statistically significant superiority of one option over another. The benefits of A / A tests can be read, for example,here . Measured error percentage stat. the test was compared with a given theoretical value: if they roughly coincided, then everything is fine; if the measured percentage of errors is much less or much more than theoretical, then the results of such a stat. the dough is unreliable.

    To talk in more detail about the method of assessing the quality of an A / B testing system, you should first talk about the significance level and other concepts that arise when testing statistical hypotheses . Readers who are familiar with this topic can skip the next paragraph and go to the section A / B Test System Quality Assessment .

    Statistical test, confidence intervals and significance level


    Let's start with a simple example. Suppose we have only 6 users and we divided them into 2 groups of 3 people, conducted an A / B test, calculated the metric value for each individual user and obtained the following tables as a result:
    Table 1. Group A, average metric $ \ widehat {\ mu} _ {A} = \ dfrac {1} {3} $
    User
    		 Metric value
    A. Antonov1
    P. Petrov0
    S. Sergeev0

    Table 2. Group B, average metric $ \ widehat {\ mu} _ {B} = \ dfrac {2} {3} $
    User
    		 Metric value
    B. Bystrov0
    V. Volnov1
    U. Umnov1

    The average metric in group A is $ \ widehat {\ mu} _ {A} = \ dfrac {1} {3} $, in group B - $ \ widehat {\ mu} _ {B} = \ dfrac {2} {3} $, and the average value of the difference between the two groups is $ \ widehat {\ mu} _ {\ Delta} = \ widehat {\ mu} _ {B} - \ widehat {\ mu} _ {A} = \ dfrac {1} {3} $. If we restrict ourselves only to average values, it turns out that the option shown to group B won (because the difference$ \ widehat {\ mu} _ {\ Delta} $Above zero). But in each group there are only 3 values ​​- which means that we estimated the true value of the difference by 6 numbers, that is, with a large error. Therefore, the result obtained may be random and may mean nothing at all.

    That is, in addition to the difference in the average values ​​of the metric in the two groups, we would also like to estimate the confidence interval for the true value of the difference$ \ mu _ {\ Delta} $, that is, the interval in which, "most likely", lies the true meaning. The phrase "most likely" is intuitive. To formalize it, use the concept of significance level$ \ alpha $. The significance level is related to the confidence interval and reflects the degree of our confidence that the true value is within this confidence interval. The lower the significance level, the more confident we are.

    One can imagine what significance level means. If we repeat the A / A test many times, then the percentage of cases in which the A / A test will dye will be approximately equal$ \ alpha $. That is, in$ \ alpha \% $ of cases, we reject the hypothesis of equality of options, although both options are really equal (in other words, in $ \ alpha \% $cases we make a mistake of the first kind ). We have chosen a significance level of$ \ alpha = 5 \% $.

    Actually, the statistical test is just engaged in estimating the confidence interval for the difference$ \ mu _ {\ Delta} $at a given level of significance. If the confidence interval is known, then the procedure for determining the winner is simple:

    • If both boundaries of the confidence interval are greater than 0, then option B won.
    • If 0 is inside the interval, then it means a draw - none of the options won.
    • If both boundaries are less than 0, then option A won.

    For example, suppose we were somehow able to find out what for significance level $ \ alpha = 5 \% $ the confidence interval for the difference in our example is $ \ widehat {\ mu} _ {\ Delta} \ pm \ dfrac {1} {2} \ rightarrow \ dfrac {1} {3} \ pm \ dfrac {1} {2} \ rightarrow \ left [- \ dfrac {1} {6}, \ dfrac {5} {6} \ right] $. That is, the true meaning of the difference$ \ mu _ {\ Delta} $ most likely lies within the interval $ \ left [- \ dfrac {1} {6}, \ dfrac {5} {6} \ right] $. Zero belongs to this interval - which means that we have no reason to believe that one of the options is better than the other (in fact, one of the options may be better than the other, we simply do not have enough data to confirm this with a significance level of 5%) .

    It remains for us to understand how a statistical test estimates the confidence intervals from the significance level and experimental data for the difference in the metric between groups A and B.

    Confidence Interval Determination



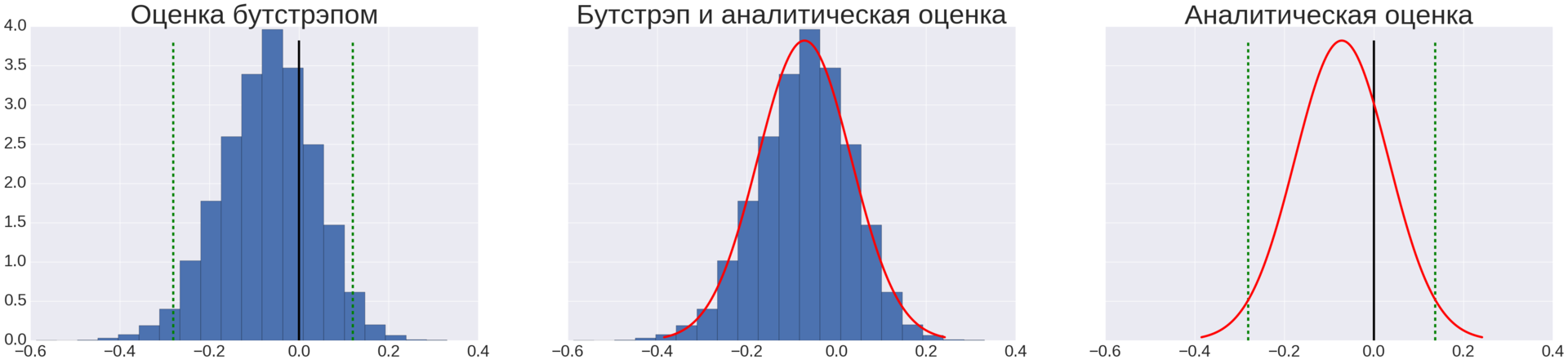
    Figure 3. Estimation of confidence intervals for the difference $ \ mu _ {\ Delta} $using bootstrap (left chart, 10,000 bootstrap iterations) and analytically (right chart). The green line shows the boundaries of the confidence interval, the black line shows the position of zero. On an average chart, both methods are combined for comparison.

    To determine the confidence intervals, we used two methods, shown in Figure 3:

    • Analytically.
    • Using bootstrap.

    Confidence Interval Analytical Assessment


    In the analytical approach, we rely on the statement of the central limit theorem (CLT) and expect that the difference in the mean values ​​of the metrics in the two groups will have a normal distribution, with parameters $ \ mu _ {\ Delta} $ and $ \ sigma _ {\ Delta} $. Exact values$ \ mu _ {\ Delta} $ and $ \ sigma _ {\ Delta} $ we do not know, but we can calculate approximate estimates $ \ widehat {\ mu} _ {\ Delta} $ and $ \ widehat {\ sigma} _ {\ Delta} $:

    $ \ begin {eqnarray *} \ widehat {\ mu} _ {\ Delta} & = & \ widehat {\ mu} _B - \ widehat {\ mu} _A \\ \ widehat {\ sigma} _ {\ Delta} & = & \ sqrt {\ widehat {\ sigma} _A ^ 2 + \ widehat {\ sigma} _B ^ 2} \ end {eqnarray *} $


    Where are the average values ​​($ \ widehat {\ mu} _A, \ widehat {\ mu} _B $) and variance of mean values ​​($ \ widehat {\ sigma} _A, \ widehat {\ sigma} _B $) are calculated
    according to standard formulas.

    $ \ begin {eqnarray *} \ widehat {\ mu} _A & = & \ dfrac {1} {N_A} \ sum_ {i = 1} ^ {N_A} x_i \\ \ widehat {\ mu} _B & = & \ dfrac {1} {N_B} \ sum_ {j = 1} ^ {N_B} x_j \\ \ widehat {\ sigma} _A ^ 2 & = & \ dfrac {1} {N_A (N_A - 1)} \ sum_ {i = 1} ^ {N_A} (x_i - \ widehat {\ mu} _A) ^ 2 \\ \ widehat {\ sigma} _B ^ 2 & = & \ dfrac {1} {N_B (N_B - 1)} \ sum_ { j = 1} ^ {N_B} (x_j - \ widehat {\ mu} _B) ^ 2 \ end {eqnarray *} $



    Knowing the parameters of the normal distribution and the significance level, we can calculate confidence intervals. We do not give formulas for calculating confidence intervals, but the idea is shown in Figure 3 on the right graph.

    One of the drawbacks of this approach is the fact that in the CLT random variables are assumed to be independent. In reality, this assumption is often violated, in particular, due to the fact that the actions of one user are dependent. For example, an Amazon user who buys one book is likely to buy another. It would be a mistake to consider two purchases of one user to be independent random variables, because we can get too optimistic estimates as a resultat confidence interval. And this means that in reality, the percentage of false A / A tests that can be stained can be many times greater than the specified value. That is what we have observed in practice. Therefore, we tried another method for estimating confidence intervals, namely bootstrap.

    Confidence Interval Estimation Using Bootstrap


    Bootstrap is one of the methods of nonparametric estimation of confidence intervals in which no assumptions are made about the independence of random variables. Using bootstrap to assess confidence intervals comes down to the following procedure:

    1. To repeat $ N _ {\ textrm {bootstrap}} $ time:

      • using bootstrap, select random subsamples of values ​​from groups A and B;
      • calculate average difference $ \ widehat {\ mu} _ {\ Delta_i} $ in these subsamples;

    2. Sort ascending values ​​obtained at each iteration
    3. Using an ordered array $ \ left [\ widehat {\ mu} _ {\ Delta_1}, \ widehat {\ mu} _ {\ Delta_2}, ~ \ dots ~ \ widehat {\ mu} _ {\ Delta_ {N _ {\ textrm {bootstrap} }}} \ right] $ determine the confidence interval so that $ \ sim (1- \ alpha) \ cdot N _ {\ textrm {bootstrap}} $points lay inside the interval. That is, the left border of the interval will be a number with an index
      $ \ dfrac {\ alpha} {2} \ cdot N _ {\ textrm {bootstrap}} $, and the right border is a number with an index $ (1 - \ dfrac {\ alpha} {2}) \ cdot N _ {\ textrm {bootstrap}} $ in an ordered array.

    Figure 3 on the left graph shows a histogram for an array of difference values ​​obtained after 10,000 bootstrap iterations, and confidence intervals calculated by the procedure described here.

    A / B Test System Quality Assessment


    So, we divided all users into $ N_ \ textrm {groups} $groups, prepared a statistical test and chose the metric we want to improve. Now we are ready to evaluate the quality of the A / B testing system. At HeadHunter we were interested in how often the stat. the test will make a mistake of the first kind, that is, what percentage of A / A tests will be stained (we denote this value$ \ alpha ^ \ textrm {real} $) at a fixed level of significance $ \ alpha $.

    Calculate$ \ alpha ^ \ textrm {real} $we can do a lot of A / A tests. As a result, we can get three options:

    1. If $ \ alpha ^ \ textrm {real} \ ll \ alpha $, then either stat. test, or the selected metric is too conservative. That is, A / B tests have low sensitivity (“persistent tin soldier”). And this is bad, because in the process of operating such an A / B testing system, we will often reject changes that really improved something, because we did not feel improvement (that is, we will often make a mistake of the second kind ).
    2. If $ \ alpha ^ \ textrm {real} \ gg \ alpha $, then either stat. test, or the selected metric is too sensitive ("Princess and the Pea"). This is also bad, because in the process of operation we will often accept changes that actually did not affect anything (that is, we will often make a mistake of the first kind ).
    3. Finally, if $ \ alpha ^ \ textrm {real} \ approx \ alpha $, then stat. the test along with the selected metric show good quality and such a system can be used for A / B testing.

    (a) We sort through all possible pairs(b) Randomly split into disjoint pairs
    Figure 4. Two options for splitting 4 user groups ($ G_1 $, $ G_2 $, $ G_3 $, $ G_4 $) for couples.

    So, we need to do a lot of A / A tests to better estimate the percentage of stat errors. test$ \ alpha ^ \ textrm {real} $. To do this, we need a large number of pairs of user groups. But where can I get a large number of pairs if all users are distributed among a small number of groups (we distributed users into 64 groups). The first thing that comes to mind is to make up all kinds of pairs of groups. If the number of user groups is equal to$ N_ \ textrm {groups} $, then we can make them $ \ dfrac {N_ \ textrm {groups} (N_ \ textrm {groups} - 1)} {2} $different pairs (the pairing scheme for 4 groups is shown in Figure 4 (a)).

    However, this approach has a serious drawback , namely: we get a large number of dependent pairs. For example, if in one group the average value of the metric is very small, then most A / A tests for pairs containing this group will turn red. Therefore, we settled on the approach shown in Figure 4 (b), in which all groups are divided into disjoint pairs. That is, the number of pairs is equal$ \ dfrac {N_ \ textrm {groups}} {2} $. The steam turned out to be much less than in the first method, but now they are all independent.

    The results of applying the A / A test to 64 user groups, which are divided into 32 independent pairs, are shown in Figure 5. From this figure it is clear that out of 32 pairs, only 2 were dyed, that is$ \ alpha ^ \ textrm {real} = 2/32 \ cdot 100 \% \ approx 6 \% $.


    Figure 5. Results of A / A tests for 64 user groups randomly divided into 32 pairs. Confidence intervals were calculated using bootstrap, significance level - 5%.

    Histograms of Values$ \ left [\ widehat {\ mu} _ {\ Delta_1}, \ widehat {\ mu} _ {\ Delta_2}, ~ \ dots ~ \ widehat {\ mu} _ {\ Delta_ {N _ {\ textrm {bootstrap} }}} \ right] $obtained by bootstrap are shown in blue for non-stained pairs, yellow for stained; Gaussian distribution with analytically calculated parameters is shown in red. The black line indicates the position of zero.

    In principle, this could have been stopped. We have a way to calculate the real percentage of stat errors. test. But in this method we were confused by a small number of A / A tests. A 32 A / A test seems to be not enough for reliable measurement$ \ alpha ^ \ textrm {real} $. So, it remains for us to answer the following question:

    If the number of pairs is small, then how can we reliably measure$ \ alpha ^ \ textrm {real} $?

    We used this solution: let's randomly redistribute users into groups many times. And after each redistribution, we can measure the percentage of errors$ \ alpha ^ \ textrm {real} _ {i} $. The average of all measured values ​​will give an estimate of$ \ alpha ^ \ textrm {real} $.

    As a result, we received the following procedure for assessing the quality of the A / B testing system:

    1. To repeat $ N_ \ textrm {iterations} $ time:

      • Randomly distribute all users by $ N_ \ textrm {groups} $ to groups;
      • Accidentally smash $ N_ \ textrm {groups} $ groups on $ \ dfrac {N_ \ textrm {groups}} {2} $ steam;
      • For all pairs, conduct an A / A test and calculate the percentage of stained pairs $ \ alpha ^ \ textrm {real} _i $ on this $ i $th iteration

    2. calculate $ \ alpha ^ {\ textrm {real}} $ as the average of all iterations:

      $$ display $$ \ begin {equation *} \ alpha ^ {\ textrm {real}} = \ dfrac {1} {N_ \ textrm {iterations}} \ sum_ {i = 1} ^ {N_ \ textrm {iterations} } \ alpha ^ \ textrm {real} _i \ end {equation *} $$ display $$



    If in the procedure for assessing the quality of the A / B testing system, we fix the stat. test (for example, we will always use bootstrap) and believe that the stat itself. Since the test is infallible (or indispensable), then we get a system for evaluating the quality of metrics .

    An example of the quality assessment of one of the metrics is shown in Figure 6. From this graph it can be seen that the average percentage of errors is stat. test (i.e. value$ \ alpha ^ \ textrm {real} $) almost perfectly matches the set value $ \ alpha = 5 \, \% $. It is worth noting that such a good coincidence we saw infrequently. We consider it a good coincidence if$ 3 \, \% \ leq \ alpha ^ \ textrm {real} \ leq 8 \, \% $.


    Figure 6. Quality assessment result for metrics of successful user actions. Blue bar graph for an array of numbers$ \ left [\ alpha ^ \ textrm {real} _1, \ alpha ^ \ textrm {real} _2 ~ \ dots ~ \ alpha ^ \ textrm {real} _ {N_ \ textrm {iterations}} \ right] $, green - the average value of the array, black - the specified significance level for the bootstrap (the number of bootstrap iterations is 10,000). The number of user group pairs is 32. The number of iterations of the quality assessment procedure$N_\textrm{iterations}=1000$.

    Metric Quality Assessment Results





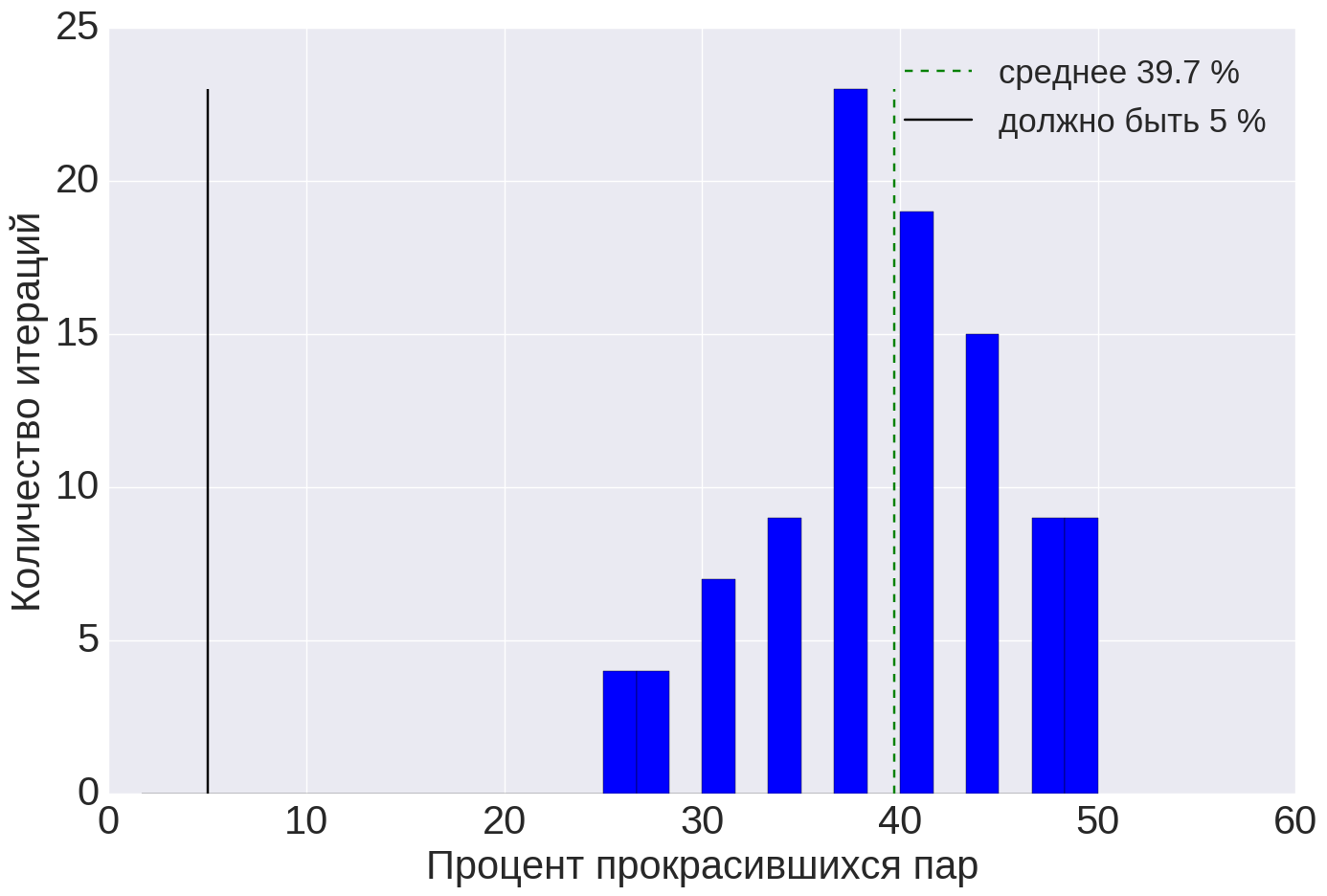    (a)
    		 (b)
    		 (in)
    Figure 7. Quality assessment results for the search session success metric: (a) for the initial metric and bootstrap by values, (b) for the original metric and bootstrap by users, (c) for the modified metric and bootstrap by values.

    When we applied the quality assessment procedure to the metric of success of search sessions, we got the result as in Figure 7 (a). Stat. the test in theory should be mistaken in 5% of cases, but in reality it is mistaken in 40% of cases! That is, if we use this metric, then 40% of the A / B tests will be stained, even if option A is no different from option B.

    This metric turned out to be a “pea princess”. However, we still wanted to use this metric, since its meaning has a simple interpretation. Therefore, we began to understand what could be the problem and how to deal with it.

    We suggested that the problem may be related to the fact that several values ​​that are dependent on one user fall into the metric. An example of a situation where two numbers from one user (Ivan Ivanovich) fall into the metric is shown in table 3.
    Table 3. An example of several values ​​in a metric from one user
    User
    		 Metric value
    Ivan Ivanovich0
    Ivan Nikiforovich0
    Anton Prokofievich1
    Ivan Ivanovich1

    We can weaken the influence of the dependence of the values ​​of one user either by modifying the stat. test, or by changing the metric. We tried both of these options.

    Modification of stat. test


    Since the values ​​are dependent on one user, we performed the bootstrap not by the values, but by the users: if the user fell into the bootstrap selection, then all of its values ​​are used; if not hit, then none of its values ​​are used. The use of such a scheme led to a significant improvement (Figure 7 (b)) - the real percentage of stat errors. test at 100 iterations turned out to be equal$\alpha^{\textrm{real}}=4.8\%$which is very close to the theoretical value $\alpha=5.0\%$.

    Metric Modification


    If it bothers us that several dependent values ​​fall into the metric from one user, then you can first average all the values ​​inside the user so that only one number falls into the metric from each user. For example, table 3 after averaging the values ​​inside each user will go to the following table:
    Table 4. Example of aggregation of values ​​within each user
    User
    		 Metric value
    Ivan Ivanovich0.5
    Ivan Nikiforovich0
    Anton Prokofievich1

    The results of evaluating the quality of the metric after this modification are shown in Figure 7 (c). The percentage of cases in which stat. the test was wrong, it was almost 2 times lower than the theoretical value$\alpha=5.0\%$. That is, for a given metric$\alpha^\textrm{real}$ and $\alpha$ not perfect match, but it is much better than the initial situation in Figure 7 (a).

    Which of the two approaches is better


    We used both approaches (modification of the statistical test and modification of the metric) to assess the quality of various metrics, and for the vast majority of metrics, both approaches showed good results. Therefore, you can use the method that is easier to implement.

    conclusions


    The main conclusion that we made when assessing the quality of the A / B testing system: it is imperative to perform an assessment of the quality of the A / B testing system) Before using the new metric, you need to check it. Otherwise, A / B tests run the risk of becoming a form of divination and damage the development process.

    In this article, we tried, as far as possible, to provide all the information about the device and the principles of the procedure for assessing the quality of the A / B testing system used by the company. But if you still have questions, feel free to ask them in the comments.

    PS


    I would like to express my gratitude to lleo for systematizing the A / B testing process in the company and for conducting proof-of-concept experiments, the development of which is this work, and p0b0rchy for the transfer of experience, patient many hours of explanation and for generating the ideas that formed the basis our experiments.
    Tags:

    Also popular now: