Classical maze generation algorithms. Part 1: Introduction
- Tutorial
Foreword
The almost complete lack of materials in Russian about algorithms for generating labyrinths prompted me to write an article. On Habré, from what is generally on a subject, two articles can be noted: one and two . The value and benefit of which is only the second. In the first - just a translation of the formal algorithm and a small explanation of it. Which, of course, is not bad, but very scarce and does not cause a desire to study the topic further.
If you like my article, I will continue to write about various algorithms. We will consider the two most primitive and simple cases - binary tree generation and Sidewinder, which, in essence, is just a slightly modified version of the binary tree with one noticeable plus. CAUTION TRAFFIC .
I'll give you one piece of advice - do not peek at the code until you write your implementation. You will get much more pleasure and benefit from fixing bugs and finding errors than if you simply translate from one language to another.
Seriously. Take advice. You, true, spend more time, but it is worth it. For example, due to a couple of errors, I got a very funny generator of “alien” texts that can be used in various Sci-Fi games to create text. I hope you are studying the topic for yourself and do not rush anywhere.
PS:
I will use the term “ displacement ” to mean English bias. Those. addiction of the algorithm to direction in any direction. For example, right shift - the algorithm generates mazes with long right passages.
Coloring of the labyrinths occurs relative to the distance from the extreme left corner of the field to a certain cell. The farther from the origin, the darker the color.
An ideal labyrinth is a labyrinth in which one cell is connected to another in one single way. In other words, a spanning tree.
About Lua
When I was just starting to dig into the topic of mazes, I did not expect that in the end I would write an article and choose a language in which I have the opportunity not to spend too much time on rendering and architecture and deal exclusively with logic. As a result, between C ++ and Lua, the choice fell on Lua and Love2D.
Do not worry if you are unfamiliar with Lua. Ignorance of the language does not prevent you from understanding the implementation, due to the simplicity of the syntax. If you know how to program at least a little, 80% of the code will not cause you problems with understanding. The remaining 20% is language specific, about which I will always write at the beginning of the article, explaining their work.
The first thing I should say:
Lua has only one data structure - tables - an associative array with which we create the structures we need. For example, classes, sets, regular arrays, stacks, queues, and the like. We can access them using either lowercase keys or indexes.
Also, tables do not limit us in storing only one data type in one object and work similar to structures in C / C ++. Such a code is absolutely correct:
Assigning nil will remove the field:
Second:
Lua does not have a hidden table copy mechanism. The code below will not copy and create a new SomeNewArray object, it will only copy the reference to the SomeArray object into it, and therefore, it will change it in the same way as if you pass the value through an non-constant link or pointer in C / C ++:
And third, for those who are familiar with Lua:
Yes, I know that in some places the code is redundant. And the fact that in some places everything could be simplified by metamethods too. It should be borne in mind that the code was written primarily in order to understand the algorithms, and not for use in a real project. In addition, the absence of an excess of language-specific functions allows you to lay out the code in the form in which it is, without heaps of comments.
Do not worry if you are unfamiliar with Lua. Ignorance of the language does not prevent you from understanding the implementation, due to the simplicity of the syntax. If you know how to program at least a little, 80% of the code will not cause you problems with understanding. The remaining 20% is language specific, about which I will always write at the beginning of the article, explaining their work.
The first thing I should say:
Lua has only one data structure - tables - an associative array with which we create the structures we need. For example, classes, sets, regular arrays, stacks, queues, and the like. We can access them using either lowercase keys or indexes.
Also, tables do not limit us in storing only one data type in one object and work similar to structures in C / C ++. Such a code is absolutely correct:
ourStructure = {}
ourStructure[“BeautyKey”] = 42
ourStructure[42] = “UltimateAnswer”
ourStructure[1] = falseAssigning nil will remove the field:
ourStructure[42] = nilSecond:
Lua does not have a hidden table copy mechanism. The code below will not copy and create a new SomeNewArray object, it will only copy the reference to the SomeArray object into it, and therefore, it will change it in the same way as if you pass the value through an non-constant link or pointer in C / C ++:
someArray = {}
someArray[1] = 42
someArray[2] = “ReferencesTest”
someNewArray = someArray
someNewArray[1] = “42 Is Gone, Now Only the Garbage-String here”And third, for those who are familiar with Lua:
Yes, I know that in some places the code is redundant. And the fact that in some places everything could be simplified by metamethods too. It should be borne in mind that the code was written primarily in order to understand the algorithms, and not for use in a real project. In addition, the absence of an excess of language-specific functions allows you to lay out the code in the form in which it is, without heaps of comments.
Binary tree algorithm




Description :
The very first and simplest algorithm in understanding, which I will consider. Its essence is to pave the way in a random direction from each cell of the field: in my implementation, either up or to the right (depending on the offset you choose). We process only 1 cell per unit of time, therefore, we can generate labyrinths of infinite size, preserving only the final result (labyrinth) without the need to store any secondary information.
This generation method has two side effects:
1. Labyrinths have a strong diagonal displacement and the absence of dead ends in its direction. Look at the screenshots above and you will see that each of the corridors tends to the upper right cell, and, as a result, has exactly one path to it, and there is no dead end anywhere:
2. Two empty corridors on the sides of the maze. When the algorithm “digs” to the end of the row / column, it has no choice but to continue the path in one single direction, creating empty “borders”.
By the way, the name does not just coincide with the data structure. The result of his work is a random binary tree in which from each cell (vertex) there is exactly 1 path towards the root (parent vertex), and, accordingly, exactly 1 path to any other cell. As a result, any cell has no more than 3 connections with its neighbors.
Formal algorithm (for northeast bias):
- Select an initial cell;
- Choose a random direction to pave the way. If a neighboring cell in this direction goes beyond the boundaries of the field, dig a cell in the only possible direction;
- Go to the next cell;
- Repeat 2-3 until all cells have been treated;
Work example
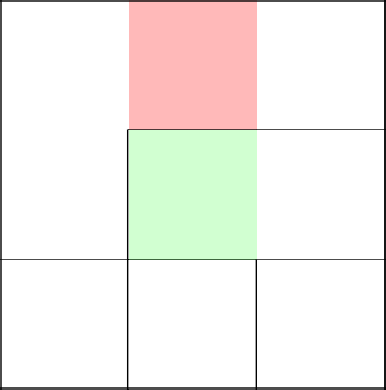
Green is the current cell in question, red is the front, cells in which you can move.
We start with the coordinate (0; 0). We cannot go upstairs in this row, because otherwise we will go beyond the boundaries of the maze. We go right to the stop, demolishing all the walls along the way.

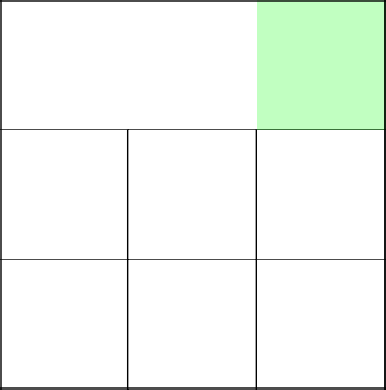
That's it, dead end. Nowhere to go. We move to the next row and see that now there is the opportunity to go up and to the right.

Throw a coin and choose ... Top. We remove the wall and move on to the next cell.
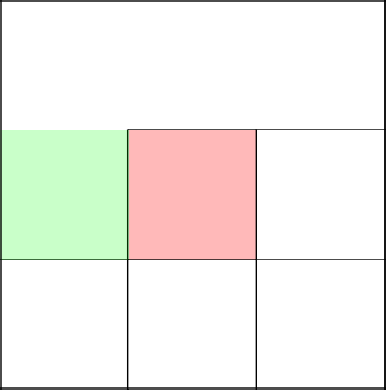
Excellent. Chance tells us to go right. We remove the wall and move to the next cell.
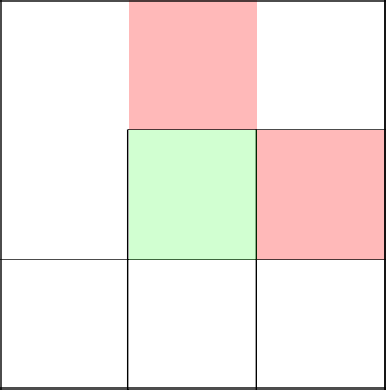

We have no choice, we cannot go left, which means we remove the wall from above and go to the next row.

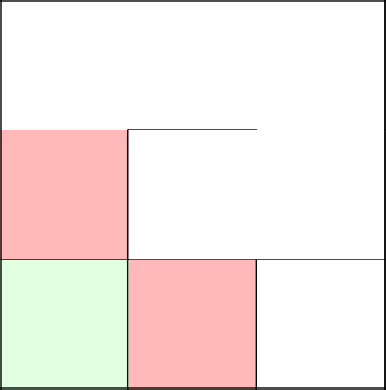
The coin convinces us to go right. Well, listen. We remove the wall and go to the next cell.
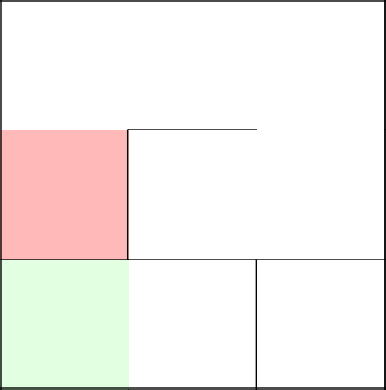
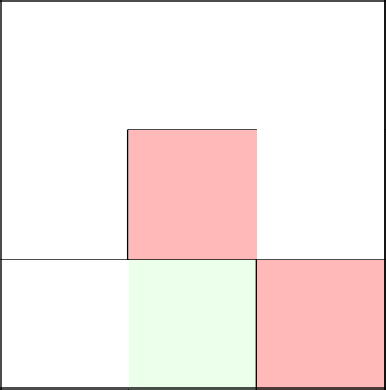
Having rolled a meter, our unfortunate piece of metal falls and says that it is time to go up. We demolish the wall, step to the next cell, and, since it is the last in this row, we remove the wall from above. The labyrinth is over.



We start with the coordinate (0; 0). We cannot go upstairs in this row, because otherwise we will go beyond the boundaries of the maze. We go right to the stop, demolishing all the walls along the way.


That's it, dead end. Nowhere to go. We move to the next row and see that now there is the opportunity to go up and to the right.

Throw a coin and choose ... Top. We remove the wall and move on to the next cell.

Excellent. Chance tells us to go right. We remove the wall and move to the next cell.



We have no choice, we cannot go left, which means we remove the wall from above and go to the next row.


The coin convinces us to go right. Well, listen. We remove the wall and go to the next cell.


Having rolled a meter, our unfortunate piece of metal falls and says that it is time to go up. We demolish the wall, step to the next cell, and, since it is the last in this row, we remove the wall from above. The labyrinth is over.



Pros :
- Simple implementation;
- High speed;
- The ability to generate endless mazes;
Cons :
- Low complexity of the picture;
- Strong diagonal shift;
- Lack of deadlocks on shift;
- The uniformity of the generated labyrinths;
Implementation
local mod = {}
local aux = {}
aux.width = false
aux.height = false
aux.sx = false
aux.sy = false
aux.grid = false
function aux.createGrid (rows, columns)
local MazeGrid = {}
for y = 1, rows do
MazeGrid[y] = {}
for x = 1, columns do
MazeGrid[y][x] = {bottom_wall = true, right_wall = true} -- Wall grid
end
end
return MazeGrid
end
-- Binary Tree North-East variant
function mod.createMaze(x1, y1, x2, y2, grid)
aux.width, aux.height, aux.sx, aux.sy = x2, y2, x1, y1
aux.grid = grid or aux.createGrid(aux.height, aux.width)
aux.binarytree()
return aux.grid
end
function aux.binarytree()
for y = aux.sy, aux.height do
for x = aux.sx, aux.width do
if y ~= aux.sy then
if math.random(0, 1) == 0 then
if x ~= aux.width then
aux.grid[y][x].right_wall = false
else
aux.grid[y-1][x].bottom_wall = false
end
else
aux.grid[y-1][x].bottom_wall = false
end
else
if x ~= aux.width then
aux.grid[y][x].right_wall = false
end
end
end
end
end
return mod
Sidewinder Algorithm



Description :
The algorithm with the untranslatable name Sidewinder in its work is very similar to the binary tree algorithm, in the difference that it does not have a characteristic diagonal shift, we consider one empty corridor and cell not individually, but in sets. Labyrinths are obtained with a predominantly vertical or horizontal displacement (depending on implementation), with no dead ends in their direction. Compared to its more primitive counterpart, the displacement is not so noticeable and more like a “spiral” that smoothly replaces vertical and horizontal corridors.
In terms of side effects, Sidewinder creates only one empty hallway on one side, instead of two. Starting to create sets from the first row of the field, we don’t have the opportunity to dig up the path, since we are in the most extreme vertical position and an attempt to go higher will lead to going beyond the boundaries of the field. But even if we organize the sets without going vertically, we will create several areas isolated from each other.
For example: 9 cells of the first row can be divided into three sets, between which the walls are located. Each set of the second row will dig a path to one of the three “blocks” above. The third row will pave the way to the "blocks" of the second. And so on until the end of the field. As a result, we get 3 branched, isolated from each other vertical areas, which is not suitable for an ideal maze, in which from each point of the field there is exactly 1 path to any other.
Formal algorithm (for standard bias):
- Choose the starting row;
- Select the starting cell of the row and make it current;
- Initialize an empty set;
- Add the current cell to the set;
- Decide whether to pave the way to the right;
- If paved, then go to the new cell and make it current. Repeat steps 3-6;
- If you haven’t paved, select a random cell of the set and pave the way up from there. We go to the next row and repeat 2-7;
- Continue until each row has been processed;
Work example
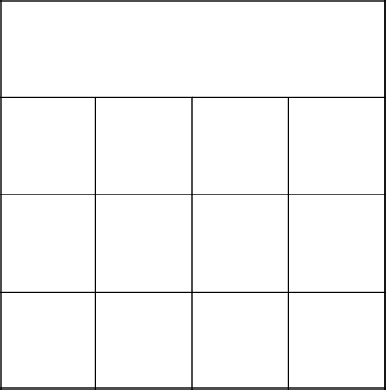
Red cells are members of the multitude.
We start from the first row and see that above us - going beyond the field. We tear down all the walls and go immediately to the second row, create an empty set.

So, and here it is more interesting. Let's add the first two cells of the row to the set.
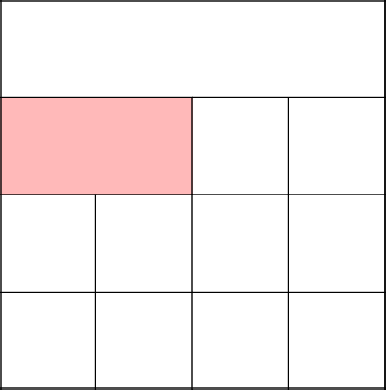
We select one of these cells and remove the upper wall belonging to it in the first row.

Zero the set, add the next cell of the row to it.
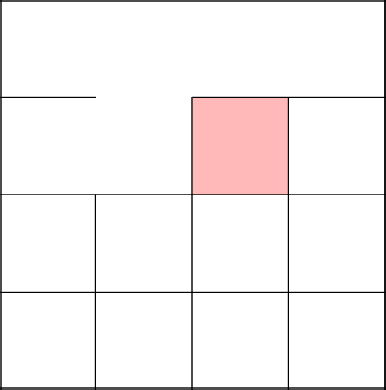
This time we are not uniting with anyone, we are simply paving the way up directly from this single cell.

We repeat our actions. Zero the set, move to the next cell, add it ... And since it remains the last in the row, we also remove the wall from above and go to the row below.
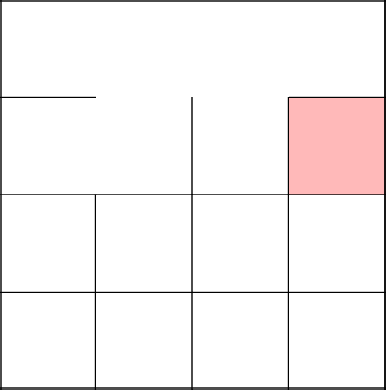

And now immediately combine the first three cells into one set.

We randomly select a cell, in our case, the second one and remove the wall from above to the previous row.

Well, here again we have no choice, we remove the wall above and go a row below.
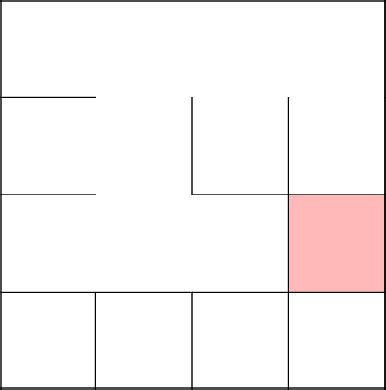

This time, we will make the very first cell the only one. We remove the wall to the previous row and move on to the next cell.
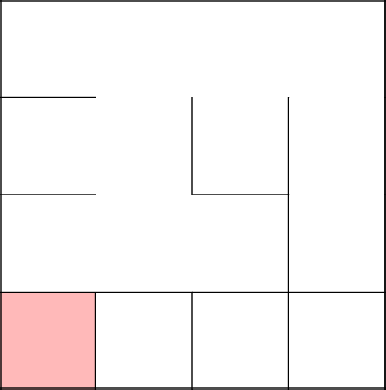

Suppose you want to combine three cells at the end.
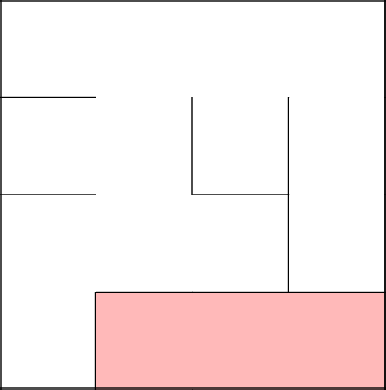
And again we liked the middle cell from the set, from which we remove the wall up. Everything, our labyrinth is ready.

We start from the first row and see that above us - going beyond the field. We tear down all the walls and go immediately to the second row, create an empty set.


So, and here it is more interesting. Let's add the first two cells of the row to the set.

We select one of these cells and remove the upper wall belonging to it in the first row.

Zero the set, add the next cell of the row to it.

This time we are not uniting with anyone, we are simply paving the way up directly from this single cell.

We repeat our actions. Zero the set, move to the next cell, add it ... And since it remains the last in the row, we also remove the wall from above and go to the row below.


And now immediately combine the first three cells into one set.

We randomly select a cell, in our case, the second one and remove the wall from above to the previous row.

Well, here again we have no choice, we remove the wall above and go a row below.


This time, we will make the very first cell the only one. We remove the wall to the previous row and move on to the next cell.


Suppose you want to combine three cells at the end.

And again we liked the middle cell from the set, from which we remove the wall up. Everything, our labyrinth is ready.

Pros :
- The ability to generate endless mazes;
- Only 1 empty hallway;
- A more complex picture, unlike the binary tree algorithm;
Cons :
- More confusing implementation;
- Lack of deadlocks on shift;
- Strong vertical displacement;
Implementation
local mod = {}
local aux = {}
aux.width = false
aux.height = false
aux.sx = false
aux.sy = false
aux.grid = false
function aux.createGrid (rows, columns)
local MazeGrid = {}
for y = 1, rows do
MazeGrid[y] = {}
for x = 1, columns do
MazeGrid[y][x] = {bottom_wall = true, right_wall = true}
end
end
return MazeGrid
end
function mod.createMaze(x1, y1, x2, y2, grid)
aux.height, aux.width, aux.sx, aux.sy = y2, x2, x1, y1
aux.grid = grid or aux.createGrid(y2, x2)
aux.sidewinder()
return aux.grid
end
function aux.sidewinder()
local cx = aux.sx --[[ cx – координата начала множества по x. У нас нет надобности создавать отдельный массив для сета, так как его элементы всегда располагаются строго в ряд ]]
for y = aux.sy, aux.height do
for x = aux.sx, aux.width do
if y ~= aux.sy then
if math.random(0, 1) == 0 and x ~= aux.width then
aux.grid[y][x].right_wall = false
else
aux.grid[y-1][math.random(cx, x)].bottom_wall = false
if x ~= aux.width then
cx = x+1
else
cx = aux.sx
end
end
else
if x ~= aux.width then
aux.grid[y][x].right_wall = false
end
end
end
end
end
return mod
Epilogue
I hope you enjoyed the article and gained new knowledge about the primitive procedural generation of labyrinths. I chose the two easiest algorithms to implement and operate, so that it’s easier for beginners to “touch” a topic and see if they want to study it further. It is important for me to know whether such articles are interesting to people on Habrahabr and whether it is worth continuing to write them. For readers, I have at least 9 more classic algorithms that are worth considering. Some of them are random walks around the field, such as the Prim or Wilson algorithm, some require more resources to work, as they work with graphs, for example, Eller and Kruskal, and some withstand the middle ground. But this is not the end - I have things in my sleeve: polar (round) mazes, the generation of mazes on a different grid (hexes, a triangle, etc.), masking of labyrinths in inscriptions and forms, 2.5D labyrinths and 3D, labyrinth theory, statistical comparison of algorithms, combined generation algorithms. In the end, we still have a great many variations of the types of labyrinths. For example, now we are considering ideal algorithms in which from each point there is exactly one path to any other. But there are also those that allow one cell to have several paths for any other! For example, Quake, Doom, and other shooters in the nascent genre used such algorithms to generate levels, according to some rumors. in which from each point there is exactly one path to any other. But there are also those that allow one cell to have several paths for any other! For example, Quake, Doom, and other shooters in the nascent genre used such algorithms to generate levels, according to some rumors. in which from each point there is exactly one path to any other. But there are also those that allow one cell to have several paths for any other! For example, Quake, Doom, and other shooters in the nascent genre used such algorithms to generate levels, according to some rumors.
Therefore, if you liked the article, the topic, and you want to see them further, then please write about it in the comment. Also, I will be very happy with any criticism, both technically and linguistically and stylistically.
