(Note: the algorithms given in the article refer to the names of degrees of a thousand on a short scale .)

Some time ago I got the opportunity to participate in the development of a game in the idle genre . What is an idle game? If this is your first time hearing about this fast-paced genre , try playing Adventure Capitalist . The Gamasutra website also has several articles ( 1 , 2 , 3 , 4 ) that allow you to look at the genre a little deeper.

One of the problems that the idle game developer will inevitably encounter is how to place all these huge numbers on the screen, and, more importantly, how the player can figure them out. In this article we will see how you can rewrite very long numbers as strings that will be convenient for players. This process can be divided into two main parts:

1. First, we will represent the number in exponential notation . Some idle game developers dwell on this , and some players seem to like it . Wolfram MathWorld has a very straightforward algorithm for translating a number , which we will use. But there is another approach that you can use if you prefer to play around with bits . I just mention it, we will not consider it in this article. If you want to use it in your game, take a look at the download folder of this article, which has an easy-to-use exponential notation script:
   
   ScientificNotation.FromDouble(12340000); // .significand == 1.234; .exponent == 7
   
2. Having found the representation of a number in an exponential notation, we can choose a name for its order. This will be the main task of this article.

Download Source

The source code is available for download and ready to use in your idle games. Using it is simple:

LargeNumber.ToString (12340000); // результатом будет "12.34 million"

Also, a small sample program is included in the download files, demonstrating how large numbers are converted into strings in the game (using the button scripts described in the previous article ):



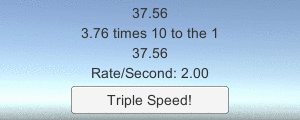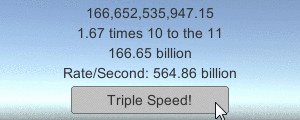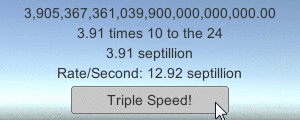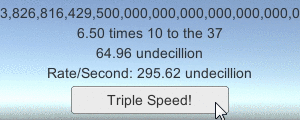
All this is part of the set of code examples that should accompany some of my articles written earlier, mainly from tutorials on working with a network in Unity ( 1 , 2 , 3 ). Download code examples to see how they work!

Standard number format strings

Numbers less than a million are quite small and do not require serious processing. You can rely on the built-in formatting capabilities of C # numbers , they will do most of the work for us: By adding the appropriate argument to the ToString method , we can almost easily group delimiters and limited decimal places. We do not need to perform additional division or use the rounding functions down .

double x = 987654.321
x.ToString ("N2"); // возвращает "987,654.32"

Latin prefixes for not very large numbers

When dealing with large numbers expressed in millions (millions), billions (billions), trillions (trillions) and so on, we know that the names change every three digits. Having a number in an exponential notation, we know that it is expressed in millions if its order is from 6 to 8, in billions - from 9 to 11, and in trillions if it is from 12 to 14, etc. In the general form for an exponential notation: We need to express N as follows: Then the final line of the number will be: where Name (U) can be obtained from this table of Latin prefixes:

M x 10N



N = 3(U+1) + V, где V < 3



M*(10^V) Name(U)+"llion"

U	Name (U)
1	mi
2	bi
3	tri
4	quadri
5	quinti
6	sexti
7	septi
8	octi
9	noni

For example, if we process the number 123,000,000,000,000,000, we can express it in an exponential notation like this: By rewriting N , we get: This means that our number looks like: Simplifying, we get:

1.23 x 1017, откуда M = 1.23 и N = 17



17 = 3*(4+1) + 2, откуда U = 4 и V = 2



1.23*(102) Name(4)+"llion"



123 quadrillion

Prefix Combinations for Large Numbers

Wikipedia has a useful article explaining how names are given to large numbers. I will not repeat what is written there. Instead, I will give a description of how to approach the algorithm and present some examples.

Having received the value of U of the number (approx. Transl .: hereinafter, the author says N, but this is clearly wrong) , as we did in numbers with Latin prefixes, we need to break it into bits (units, tens, hundreds), and then formulate name as follows:

(префикс единиц) + (модификатор) + (префикс десяток) + (префикс сотен) + (удаление "a" в конце) + "llion"

Prefixes of units, tens and hundreds can be taken from the tablein the Wikipedia article. In some cases, it is necessary to add a modifier if, in addition to certain unit prefixes, we put prefixes of tens or hundreds, but in most cases the modifier is not needed. Let's look at a few examples.

If U = 12 , then for units the figure will be 2, which corresponds to "duo" , and for tens - 1, corresponding to "deci" . When switching from "duo" to "deci" a modifier is not needed. Using the above formula, we get “duodecillion” .

If U = 27 , for units the figure is 7 (corresponds to "septe" ), for tens - 2 (corresponds to "viginti") According to the table, the transition from septe to viginti requires the modifier m . Putting it all together, we get "septemvigintillion" .

And finally, if U = 30 , then the digit for tens is 3, which corresponds to “triginta” , which has the ending “a” . Therefore, we discard it and get “trigintillion” .

If you are trying to understand how all this will look in the code, I will answer: it will be a combination of array searches, several if constructsand concatenation and string expansion operations. If you're lucky and work with a language that supports comparisons with patterns, you can use them.

The source code files contain a working implementation that processes all cases up to U = 999. It has been tested on all names included in the list of large numbers. I urge you to download them if you need ready-to-use code that can be easily inserted into your own projects, or if you want to compare your implementation with a working version.

And if U = 1000?

Then the number is called a million (approx. Transl .: in the long scale - quingentiard) .

Big numbers are not big enough

Double precision floating point numbers allow you to work with numbers up to 10 ³⁰⁸ , or U = 101. If your game requires larger numbers, then you can try to store numbers with arbitrary precision . Thus, you can make players millionaires.

But first ask yourself if you really need it. Infinity provides us with plenty of room for game development, and we don’t have to try to fill all the space we have. To paraphrase my college professor: “Think of the largest finite number you can think of. Now use the same number as his exponent, and raise that number to the power of yourself. If you now place this number on the axis of real numbers, then compared with infinity, it will still be very close to zero. "

Will your game become more interesting by going beyond double precision numbers? For some games, the answer may be positive, but in most cases I advise you to think again about the balance and design of the game ( 1 , 2 ,3 , 4 ).

If you liked the article, do not forget to download the project folder ! I hope it will be useful in developing your own game. Thanks for reading!