Stockholm City Library. Photo minotauria .

In this article I want to talk about that evaluating the memory access time as O (1) is a very bad idea, and instead we should use O (√N). First, we will consider the practical side of the issue, then the mathematical one, based on theoretical physics, and then we will consider the consequences and conclusions.

Introduction

If you studied computer science and analysis of algorithmic complexity, then you know that the passage through the linked list is O (N), the binary search is O (log (N)), and the search for an element in the hash table is O (1). What if I tell you that all this is not true? What if the passage through the linked list is actually O (N√N), and the search in the hash table is O (√N)?

Do not believe? I will convince you now. I will show that access to memory is not O (1), but O (√N). This result is valid both in theory and in practice. Let's start with practice.

Measure

Let's first determine the definitions. The “O” notation is great applicable to many things, from memory usage to running instructions. In the framework of this article, we O (f (N)) will mean that f (N) is the upper bound (worst case) in time that is needed to access N bytes of memory (or, accordingly, N elements of the same size ) I use Big O to analyze time, but not operations , and this is important. We will see that the central processor is waiting for slow memory for a long time. Personally, I don't care what the processor does while it waits. I only care about the time, how long this or that task takes, so I restrict myself to the definition above.

One more note: RAM in the header means random access (random accesses) in general, and not some specific type of memory. I consider the access time to information in memory, whether it be a cache, DRAM or swap.

Here is a simple program that goes through a linked list of size N. Sizes - from 64 items to 420 million items. Each list node contains a 64-bit pointer and 64 data bits. The nodes are mixed in memory, so each memory access is arbitrary. I measure the passage through the list several times, and then mark on the graph the time it took to access the element. We should get a flat graph of the form O (1). Here is what happens in reality:

Difficulty accessing an item in a linked list. Access to an arbitrary element in a 100-megabyte list is approximately 100 times slower than access to an element in a 10-kilob list.

Note that this graph uses a logarithmic scale on both axes, so the difference is actually huge. From about one nanosecond per element, we have reached a whole microsecond! But why? The answer, of course, is the cache. System memory (RAM) is actually quite slow, and to compensate, smart computer designers add a hierarchy of faster, closer, and more expensive caches to speed up operations. My computer has three levels of caches: L1, L2, L3 32 KB, 256 KB and 4 MB, respectively. I have 8 gigabytes of RAM, but when I ran this experiment, I only had 6 free gigabytes, so the last one started was swapping to disk (SSD). Here is the same graph, but with cache sizes.

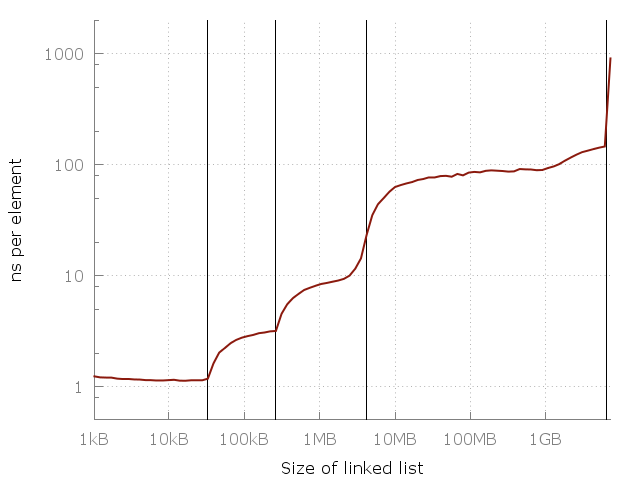
The vertical lines indicate L1 = 32 kb, L2 = 256 kb, L3 = 4 mb and 6 gigabytes of free memory.

The graph shows the importance of caches. Each cache layer is several times faster than the previous one. This is the reality of modern CPU architecture, be it a smartphone, laptop or mainframe. But where is the general pattern here? Can a simple equation be placed on this graph? It turns out we can!

Let's take a closer look, and notice that between 1 megabyte and 100 megabytes there is about a 10-fold slowdown. And the same between 100 megabytes and 10 gigabytes. It seems that every 100-fold increase in used memory gives a 10-fold slowdown. Let's add this to the chart.

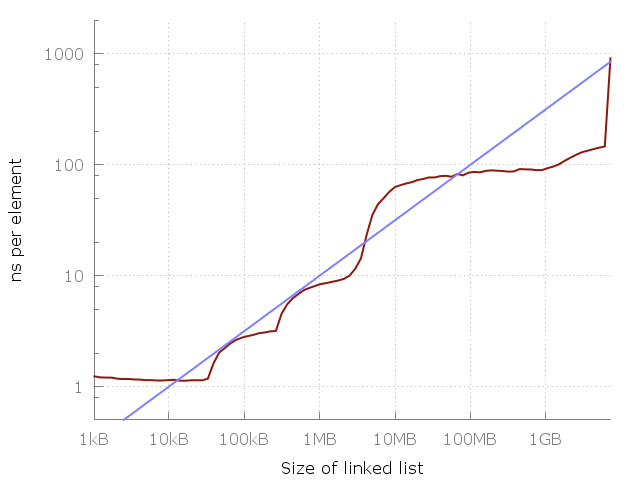
The blue line is O (√N).

The blue line in this graph indicates the O (√N) cost of each memory access. Sounds great, right? Of course, this is my specific car, and your picture may look different. However, the equation is very easy to remember, so maybe it should be used as a rough rule.

You are probably asking, what's next, to the right of the schedule? Does the rise continue or does the chart become flat? Well, it becomes flat for a while, while there is enough free space on the SSD, after which the program will have to switch to the HDD, then to the disk server, then to the distant data center, and so on. Each jump will create a new flat area, but I think the general upward trend will continue. I did not continue my experiment due to lack of time and lack of access to a large data center.

“But the empirical method cannot be used to define Big-O boundaries,” you say. Of course! Maybe there is a theoretical limit to the delay in accessing memory?

Round library

Let me describe a thought experiment. Suppose you are a librarian working in a circular library. Your table is in the center. The time you need to get any book is limited by the distance you need to travel. And in the worst case, this is the radius, because you need to get to the very edge of the library.

Suppose your sister works in another similar library, but her (the library, not her sister :), - approx. per.) the radius is twice as large. Sometimes she needs to go twice as much. But her library has an area of ​​4 times that of yours, and it contains 4 times as many books. The number of books is proportional to the square of the radius: N∝ r². And since the access time T to the book is proportional to the radius, N∝ T² or T∝√N or T = O (√N).

This is a crude analogy with a central processor that needs to get data from its library - RAM. Of course, the speed of the “librarian” is important, but here we are limited by the speed of light. For example, in one cycle of a 3-GHz processor, the light travels a distance of 10 cm. So for a round trip, any instantly available memory should be no further than 5 centimeters from the processor.

Well, how much information can we place within a certain distance r from the processor? We talked about a round flat library above, but what if it is spherical? The amount of memory that fits in the sphere will be proportional to the cube of radius - r³. In reality, computers are quite flat. This is partly a matter of form factor and partly a matter of cooling. Perhaps someday we will learn how to build and cool three-dimensional blocks of memory, but so far the practical limitation of the amount of information N within the radius r will be N ∝ r². This is true for very distant storages, such as data centers (which are distributed over the two-dimensional surface of the planet).

But is it possible, theoretically, to improve the picture? To do this, you need to learn a little about black holes and quantum physics!

Theoretical boundary

The amount of information that can be placed in a sphere of radius r can be calculated using the Beckenstein boundary . This amount is directly proportional to the radius and mass: N ∝ r · m. How massive can a sphere be? Well, what is the densest in the universe? Black hole! It turns out that the mass of the black hole is proportional to the radius: m ∝ r. That is, the amount of information that can be placed in a sphere of radius r is N ∝ r². We came to the conclusion that the amount of information is limited by the area of ​​the sphere, and not by the volume!

In short: if you try to put a very large L1 cache in the processor, then it will eventually collapse into a black hole, which will prevent the user from returning the calculation result.

It turns out that N ∝ r² is not only a practical, but also a theoretical boundary! That is, the laws of physics set a limit on the speed of access to memory: in order to get N bits of data, you need to send a message at a distance proportional to O (√N). In other words, each 100-fold increase in the task leads to a 10-fold increase in the access time to one element. And this is exactly what our experiment showed!

A bit of history

In the past, processors were much slower than memory. On average, a memory search was faster than the calculation itself. It was common practice to store tables for sines and logarithms in memory. But times have changed. Processor performance grew much faster than memory speed. Modern processors most of their time just wait for memory. That is why there are so many levels of cache. I believe that this trend will continue for a long time, so it is important to rethink the old truths.

You can say that the whole point of Big-O is in abstraction. It is necessary to get rid of such architectural details as memory latency. This is true, but I argue that O (1) is a wrong abstraction . In particular, Big-O is needed to abstract constant factors, but memory access is not a constant operation. Neither in theory nor in practice.

In the past, any memory access in computers was equally expensive, so O (1). But this is no longer true, and for quite some time now. I believe that it is time to think about it differently, forget about memory access for O (1) and replace it with O (√N).

Effects

The cost of accessing the memory depends on the size that is requested - O (√N), where N is the size of the memory that is accessed at each request. So, if the call occurs to the same list or table, then the following statement is true:

Passing through a linked list is an O (N√N) operation. Binary search is O (√N). Getting from an associative array is O (√N). In fact, any arbitrary search in any database is at best O (√N).

It is worth noting that the actions performed between operations matter. If your program works with memory of size N, then any arbitrary memory request will be O (√N). So going through a list of size K will cost O (K√N). Upon repeated passage (immediately, without resorting to another memory), the cost will be O (K√K). Hence the important conclusion: if you need to access the same memory location several times, then minimize the intervals between calls .

If you make a pass through an array of size K, then the cost will be O (√N + K), because only the first call will be arbitrary. Repeated passage will be O (K). Hence another important conclusion: if you plan to make a pass, then use an array .

There is one big problem: many languages ​​do not support real arrays. Languages ​​like Java and many scripting languages ​​store all objects in dynamic memory, and the array there is actually an array of pointers. If you pass through such an array, then the performance will not be better than when passing through a linked list. Walking through an array of objects in Java costs O (K√N) . This can be compensated by creating objects in the correct order, then the memory allocator, I hope , will place them in memory in order. But if you need to create objects at different times or mix them, then nothing will work.

Conclusion

Memory access methods are very important. One should always try to access memory in a predictable way, and minimize arbitrary memory accesses. There is nothing new here, of course, but it is worth repeating. I hope that you will adopt a new tool for thinking about the cache: accessing the memory costs O (√N). The next time you evaluate complexity, remember this idea.