What evidence can convince mathematicians if there is no rigorous proof?

The new statistical model seems to be undermining the long-accepted assumptions from number theory. How much can she be trusted if only rigorous evidence really matters?

Which points on an elliptic curve are y ² = x ³ - 4x + 1 rational? To find them, you need to draw straight lines through pairs of rational points. All points through which the lines pass will also be rational.

Recently, four researchers have come up with a model that turns the whole common sense of their field of research upside down. They used computational data, suggesting that the prevailing opinion of one of the fundamental concepts that had prevailed over several decades was wrong.

And these are not biologists, climatologists, or physicists. In their scientific field, empirical models have no right to vote on truth. They are mathematicians, representatives of the discipline, whose standard currency - the undeniable logical proof - usually relieves them of debates affecting other areas. And yet here they are, with their model saying that it is probably time to revisit some long-standing views.

The model, published online in 2016, and ready to appear in the Journal of the European Mathematical Society, refers to such a respectable mathematical concept as the rank of an algebraic equation. A rank is a measure corresponding to how many solutions of an equation are related to rational numbers, and how many to irrational ones. The equations of high rank have more sets of rational solutions, and they are more complicated.

Since the beginning of the 20th century, mathematicians have been interested in the question whether there are any restrictions on the height of the rank of the equation. At first, almost everyone thought that a restriction should exist. But by the 1970s, the prevailing opinion had changed - most mathematicians began to believe that the rank was unlimited, which means that curves with infinitely large ranks can be found. And so it was, although some mathematicians believed that there was no strong argument in support of this view.

“People very authoritatively declared no restrictions. However, when you begin to understand, it turns out that the evidence for this is extremely weak, ”said Andrew Granville , a mathematician at the University of Montreal and University College London.

Today, evidence suggests otherwise. Two years after the appearance of the model, she convinced many mathematicians that the rank of algebraic equations of a certain type was indeed limited. However, not all of this model seems convincing. The lack of agreement raises questions that are not often related to mathematical results — how much weight can empirical evidence have in an area in which only rigorous evidence matters?

“There is no mathematical justification for the fact that this model is exactly what we need,” said Jennifer Park , a mathematician at the University of Ohio, co-author of the work. “Except that from an experimental point of view, a lot of things work.”

Point to point

If they give you an equation, you can draw a curve of its solutions on the graph. Mathematicians want to know how many of these solutions are rational — they belong to the type of numbers that can be expressed as the ratio of two integers (1/2, -3 or 4483/929).

Rational solutions are hard to find systematically, but mathematicians have technicians working in certain conditions. Take the equation x ² + y ²= 1. The graph of solutions of this equation is a circle. To find all rational points of a circle, we start with one particular solution, say, from the point at which x = 1 and y = 0. Then draw a line through this point that intersects the circle at one other point. If the slope of our line is rational, then the second intersection will also be a rational solution. By drawing a line, we increased the number of rational solutions from one to two.



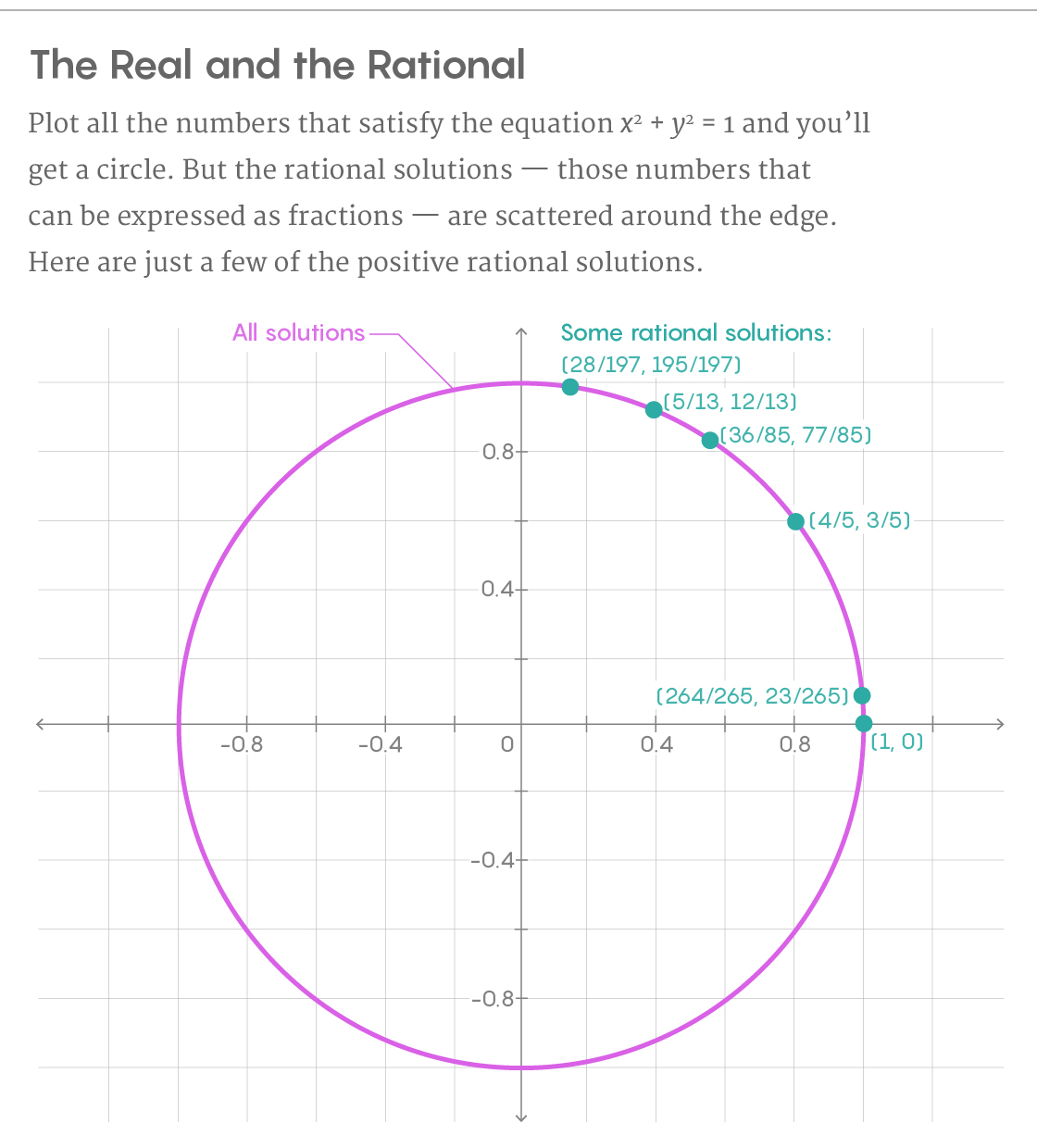
And there is no need to dwell on this. We repeat the procedure by drawing a straight line with another rational bias through the second rational point - it will cross the circle at the third rational point. Continuing so indefinitely, we eventually find all rational points of a circle of which there are infinitely many.

And in the case of a circle, you only need to start from one point, and you can find them all. The number of rational decisions that you need to know at the beginning in order to detect all the others is known as the rank of a curve. Rank is a neat way of describing an infinite set of rational solutions by one number. “This seems to be the best way to describe rational solutions to these curves,” said Bjorn Puunen , a mathematician at MIT, co-author of the model, together with Park, John Voight of Dartmouth College and Melanie Matchet Wood of the University of Wisconsin.

Circumference is a quadratic equation, or a second degree equation (“degree” means the magnitude of the largest of the powers of the terms of the equation). For more than a hundred years, mathematicians have known how to find rational solutions of second-degree equations.

The next type of equations is elliptic curves, in which there are variables raised to the third power. Elliptic curves exist in the most attractive area of ​​mathematical research. They are more complicated than second order equations, so they are interesting to study, but they are not too complicated. The modified line drawing procedure is still applicable to elliptic curves, but stops working with equations of fourth order and higher.

Elliptic curves are of different ranks. With some elliptic curves, you can start from one rational point, apply the procedure of drawing lines and not find all rational solutions. You may have to add a second rational point that is not related to the first. With it, you will begin a new procedure for drawing lines, and find a balance of rational points. The curve, in order to find all rational points of which you need to initially know two rational points, has a rank equal to two.

There is no proven limit on the rank height of an elliptic curve. The higher the rank of the equation, the more extensive and more complex is the set of rational solutions of the curve. “The rank somehow measures the complexity of the set of decisions,” said Puunen.

Yet rank escapes the attempts of mathematicians to describe it by theory. If you are given an elliptic curve, it will not have an obvious relationship between what it looks like and what its rank is. “If I have an elliptic curve, and I adjust the coefficients a little, then its rank changes dramatically,” said Park. - You can change the ratio by one, and the rank will jump a million. No one knows how ranks behave. ”

The lack of a general theory led mathematicians to retreat to the small set of evidence they have to speculate on the existence of a rank restriction. “The point of view is that there is no limit to the rank, because people have been finding more and more ranks all the time,” Granville said. The current record holder is an elliptic curve of rank 28, discovered in 2006 by Noam Elkis, a mathematician at Harvard University.

But then this new model appeared, and stated that almost certainly this is the end of the road.

Surprise at 21

To study phenomena too complex or inaccessible for direct research, scientists use models. By creating in the laboratory an analogue of a black hole, they may be able to learn something about how real black holes behave without having to walk on the edge of the event horizon.

Mathematicians do the same. A good example is the study of prime numbers. Mathematicians want to know the answer to the question of twin numbers - is there an infinite number of pairs of prime numbers that differ by 2 (3 and 5, 11 and 13). An exhaustive answer goes beyond their knowledge, but they created models that predict the frequency of twin numbers - and the answer, apparently, is that they occur an infinite number of times.

The new model does not directly study the elliptic curves themselves. She explores a mathematical object such as the core of a matrix . Kernels refer to elliptic curves, like mice to humans - not the same thing, but they are easier to study, and one can hope that they are close enough to draw conclusions about one based on experiments on others. In particular, the kernels have their own version of the rank . Having studied the distribution of the ranks of nuclei — for how many nuclei the rank is 1, for how many it is 2, and so on — four mathematicians hoped to get an idea of ​​the distribution of ranks for elliptic curves. In fact, they put the fact that the distribution of the ranks of the kernels and elliptic curves are similar to each other.


Jennifer Park, Bjorn Puunen and Melanie Wood

“The leap of faith comes into play,” Park said. “We hope that perhaps there is another set of mathematical objects, which is much more understandable, and has the same distribution of ranks as elliptic curves.”

When four researchers did this work, most of the mathematicians considered the rank unlimited. However, the model told a different story. It says that there is only a finite number of elliptic curves with a rank greater than 21. And if there is a finite number of them, then one of them has the highest rank - which means that the rank still has an upper bound. When four mathematicians saw this, they realized that they had a living result on their hands.

“This prediction did not coincide with what everyone believed in, at least what they publicly admitted,” Wood said. “No one believed that ranks could have a restriction.”

If belief in a model requires a rather serious step, then when the model reports that common sense was wrong, a step is required to take even more. However, quite a lot of evidence speaks in favor of this result. This model is based on previous models created by other mathematicians who studied various properties of elliptic curves. Those models have stood the test of time; some of these predictions have even been proven.

“Nobody suggested starting from scratch and making a new model,” said Wood. “The question was how to enrich the existing models that people already believe in.”

Another reason to believe in the model was that the rank value at 21 does not seem like an arbitrary boundary. Ten years earlier, Granville had created another model, from which it also followed that there should be only a limited number of elliptic curves with a rank above 21. The Granville model was not at all similar to the current one - and the fact that both of them gave rank 21 as significant was not very similar to a coincidence from the point of view of many mathematicians.

“We have two completely different heuristic models and both gave out the same number, 21 - this surprised people,” said Park.

Perhaps the most convincing reason that the model seems credible was the fact that its other predictions almost exactly coincided with the proven properties of elliptic curves. The generalized conclusion of the model — the existence of a finite number of elliptic curves with a rank greater than 21 — applies to all elliptic curves. However, they have certain families, for many of which mathematicians have already determined the boundaries of ranks. The model also predicted rank values ​​for many of these families, and its predictions were similar, or even exactly coincided with the boundaries that mathematicians have already defined.

“Our boundaries accurately predicted all those cases that were studied by other people,” said Park. “People are skeptical of my reports, but when I mention other coincidences, they are very surprised by this.”

Between evidence and evidence

The model has a lot of support, but not everyone believes it, and it may be wrong. The most important skeptic is Noam Elkis, a Harvard mathematician who set a record of rank for an elliptic curve. In the decades that have passed since he became Harvard’s youngest full-time professor, he has received several results indicating that there is no rank limit. "My opinion has not changed for a long time - I do not think that we are well-versed in this matter to support this or that hypothesis," Elkis wrote to me by mail.

Elkis believes that the model may work incorrectly in different ways. It takes into account randomly chosen curves, or curves in a sense, averages. However, there is evidence, including the study of Elkis himself, about the possibility of the existence of families of elliptic curves, each of which includes an infinite number of such curves, whose behavior is significantly different from the behavior of typical curves. “Heuristic models based on the expected behavior of random curves may not tell the whole story about extreme behavior,” writes Elkis.

Even one of the authors of the model is not sure about it to the end. “I would say that I feel limited in rank, like an agnostic,” Wood said. She admits that the model may be wrong for reasons voiced by Elkis. But if the model does not cope with the task, it is because it did not take into account some hidden and unexpected properties of elliptic curves. “The question is: if you do not believe in limited ranks, where exactly does the model stop working?” Said Wood.

“Most likely, they will be right if someone does not come up with some clever reason for which they are mistaken. I have no idea whether such a reason exists or not, ”said Alexander Smith, a graduate student at Harvard who works with Elkis and studies the ranks of elliptic curves.

The authors of the model do not raise its significance in dogma. They know the difference between evidence and evidence, and understand that no mountains of the first will lead to the latter. But they believe that their work, at least, provides a reasonable basis for reflection on basic mathematical concepts after a century of simple reasoning.

“Perhaps the search for higher rank elliptic curves serves as a kind of challenge for mathematicians,” said Park. Or, perhaps, mathematicians "must reconsider their opinion about what we believed in as a popular hypothesis."