June 30, 2016 at 18:05Mathematical Notation: Past and Future
- Transfer
A translation of Stephen Wolfram's post, Mathematical Notation: Past and Future (2000) . Many
thanks to Kirill Guzenko. KirillGuzenko for help in translating and preparing the publication.
Content
Summary
Introduction
History
Computers
Future
Notes
- Empirical laws for mathematical notation
- Printed versus on
- screen notation - Written notation
- Fonts and symbols
- Search for mathematical formulas
- Non - visual notation
- Evidence
- Character selection
- Frequency distribution of characters
- Parts of speech in mathematical notation
A transcript of the speech presented at the “MathML and Mathematics on the Net” section of the first International MathML Conference in 2000.
Summary
Most mathematical notations have existed for more than five hundred years. I will consider how they were developed, what happened in ancient and medieval times, what designations were introduced by Leibniz, Euler, Peano and others, how they became widespread in the 19th and 20th centuries. The question of the similarity of mathematical notation with that which combines ordinary human languages will be considered. I will talk about the basic principles that have been discovered for ordinary human languages, which of them are used in mathematical notation and which are not.
According to historical trends, mathematical notation, like natural language, could be incredibly difficult for a computer to understand. But over the past five years we have implemented in Mathematicathe ability to understand something very close to standard mathematical notation. I will talk about the key ideas that made this possible, as well as about those features in mathematical notation that we simultaneously discovered.
Large mathematical expressions — unlike fragments of plain text — often represent computational results and are automatically generated. I will talk about the processing of such expressions and what we have done to make them more understandable to people.
Traditional mathematical notation represents mathematical objects, not mathematical processes. I will talk about attempts to develop notation for algorithms, about the experience of implementing this in APL, Mathematica, in automatic proofing programs and other systems.
An ordinary language consists of lines of text; mathematical notation often also contains two-dimensional structures. The question of the application of more general structures in mathematical notation and how they relate to the limit of people's cognitive abilities will be discussed.
The scope of application of a particular natural language usually limits the scope of thinking of those who use it. I will examine how traditional mathematical notation limits the possibilities of mathematics, as well as what generalizations of mathematics may look like.
Introduction
When this conference was gathering, people thought it would be great to invite someone to give a speech on the foundations and general principles of mathematical notation. And there was an obvious candidate - Florian Caggiori - the author of a classic book called The History of Mathematical Notation . But after a small investigation, it turned out that there was a technical problem in inviting Dr. Cajori - he died at least seventy years ago.
So I have to replace it.
I suppose there weren’t any other options. Since it turns out that there is almost no one who is alive at the moment and who was engaged in basic research on mathematical notation.
In the past, mathematical notation was usually dealt with in the context of systematization of mathematics. So, Leibniz and some other people were interested in such things in the middle of the 17th century. Babbage wrote a heavy work on this subject in 1821. And at the turn of the 19th and 20th centuries, during the period of serious development of abstract algebra and mathematical logic, there was another surge of interest and activity in this topic. But after that there was almost nothing.
However, it is not particularly surprising that I became interested in such things. Because with Mathematica, one of my main goals was to take another big step in the field of systematizing mathematics. And my more general purpose regarding MathematicaIt was to extend the computing power to all types of technical and mathematical work. This task has two parts: how the calculations take place inside, and the way people direct these calculations to get what they want.
One of Mathematica 's greatest accomplishments , which most of you probably know about, is to combine a high generality of computation from the inside out and to maintain practicality based on character expression transformations, where character expressions can represent data, graphics, documents, formulas - whatever .
However, it is not enough to just do the calculations. It is also necessary that people somehow communicate Mathematicaabout what kind of calculations they want to make. And the main way to let people interact with something so complicated is to use something like a language.
Usually languages appear in the course of some phased historical process. But computer languages are very different historically. Many were created almost completely at once, often by one person.
So what does this work include?
Well, this is what this work was for Mathematica for me : I tried to imagine what kind of calculations people would do, what fragments in this computing work are repeated over and over again. And then, in fact, I gave names to these fragments and implemented them as built-in functions in Mathematica .
Basically, we started from the English language, since the names of these fragments are based on simple English words. That is, this means that a person who simply knows English can already understand something written in Mathematica .
However, of course, Mathematica is not English. It is rather a highly adapted fragment of the English language, optimized for conveying computational information to Mathematica .
One would think that perhaps it would be nice to explain with Mathematica in plain English. In the end, we already know English, so we would not have to learn something new to explain with Mathematica .
However, I believe that there are very good reasons why it is better to think in Mathematica than in English when we think about the various kinds of calculations that Mathematica performs .
However, we also know that making a computer fully understand a natural language is an extremely difficult task.
Okay, so what about mathematical notation?
Most people who work in Mathematica are familiar with at least some mathematical notation, so it would seem very convenient to explain Mathematica in the framework of the usual mathematical notation.
But one would think that this would not work. One would think that the situation would result in something resembling a situation with natural languages.
However, there is one surprising fact - he very surprised me. Unlike natural human languages, a very good approximation can be made for ordinary mathematical notation, which the computer can understand. This is one of the most serious things that we developed for the third version of Mathematica in 1997 [the current version of Wolfram Mathematica - 10.4.1 - was released in April 2016 - approx. Ed.]. And at least some of what we got is included in the MathML specification .
Today I want to talk about some general principles in mathematical notation that I happened to discover, and what this means in the context of today and the future.
In reality, this is not a mathematical problem. This is much closer to linguistics. It's not about what mathematical notation might be, but about what the mathematical notation used in reality is - how it developed in the course of history and how it is related to the limitations of human knowledge.
I think mathematical notation is a very interesting field of study for linguistics.
As you can see, linguistics mainly studied spoken languages. Even punctuation remained almost without attention. And, as far as I know, no serious studies of mathematical notation from the point of view of linguistics have ever been conducted.
Usually in linguistics there are several directions. One deals with historical changes in languages. Another study explores how language learning affects individuals. In the third, empirical models of some linguistic structures are created.
History
Let's talk about history first.
Where did all the mathematical notation that we currently use come from?
This is closely connected with the history of mathematics itself, so we will have to touch on a bit of this issue. One can often hear the opinion that today's mathematics is the only conceivable realization of it. That which could be arbitrary abstract constructions.
And over the past nine years that I was engaged in one large scientific project, I clearly understood that such a view of mathematics is not correct. Mathematics, in the form in which it is used, is a teaching not about arbitrary abstract systems. This is the doctrine of a concrete abstract system that historically arose in mathematics. And if you look into the past, you can see that there are three main areas from which mathematics emerged in the form in which we now know it - this is arithmetic , geometry and logic .
All these traditions are quite old. Arithmetic originates from the time of ancient Babylon. Geometry may also come from those times, but it was certainly already known in ancient Egypt. Logic comes from ancient Greece.
And we can observe that the development of mathematical notation - the language of mathematics - is strongly associated with these areas, especially with arithmetic and logic.
It should be understood that all three directions appeared in various areas of human life, and this greatly influenced the designations used in them.
Arithmetic probably arose from the needs of trade, for things such as, for example, counting money, and then astrology and astronomy picked up arithmetic. Geometry, apparently, arose from land surveying and similar tasks. And logic, as you know, was born out of an attempt to systematize the arguments given in natural language.
It is noteworthy, by the way, that another, very old area of knowledge, which I will mention later - grammar- Essentially never integrated with mathematics, at least until very recently.
So, let's talk about the early notation traditions in mathematics.
Firstly, there is arithmetic. And the most basic thing for arithmetic is numbers . So what notation was used for numbers?
Well, the first representation of numbers that is known for certain is die-cutting made 25 thousand years ago. It was a unary system : to represent the number 7, it was necessary to make 7 die-cuts, and so on.
Of course, we cannot know for sure what exactly this representation of numbers was the very first. I mean, we might not have found evidence of any other, earlier representations of numbers. However, if someone in those days invented some unusual representation for numbers, and placed them, for example, in cave painting, then we may never know that it was a representation of numbers - we can take it simply as what fragments of jewelry.
Thus, numbers can be represented in unary form. And the impression is that this idea has revived many times in different parts of the world.
But if you look at what happened besides this, you can find quite a few differences. This is a bit like the way different kinds of constructions for sentences, verbs, etc. are implemented in different natural languages.
And, in fact, one of the most important questions regarding numbers, which, I believe, will come up many more times - how strong should the correspondence between ordinary natural language and the language of mathematics be ?
Or the question is: it is related to positional notation and the reuse of numbers.
As you can see, in natural languages there are usually words like ten , one hundred , one thousand , one million"and so on. However, in mathematics we can represent ten as" one zero zero "(10), one hundred as" one zero zero "(100), a thousand as" one zero zero zero "(1000) and so on. We can reuse use this one digit and get something new, depending on where it will appear in the
number.Well, this is a difficult idea, and it took people thousands of years to really accept and realize it. And their inability to accept it previously had big consequences in the notation used by them both for numbers and for other things,
as is often the case in history and, true ideas appear very early and for a long time remain in oblivion. More than five thousand years ago, the Babylonians,positional representation of numbers . Their number system was six-decimal , and not decimal , as we have. We inherited from them the presentation of seconds, minutes and hours in the current form. But they had the idea of using the same numbers to denote factors of various degrees of sixty.
Here is an example of their notation.
From this picture you can understand why archeology is so difficult. This is a very small piece of burnt clay. About half a million of these Babylonian tablets were found. And about one in a thousand — that is, only about 400 — contain some kind of mathematical notation. Which, by the way, is higher than the ratio of mathematical texts to ordinary ones on the modern Internet. Generally, while MathMLnot received enough distribution, this is a rather complicated issue.
But, in any case, the small designations on this plate look slightly similar to the footprints of tiny birds. But almost 50 years ago, in the end, researchers determined that this cuneiform tablet from the time of Hammurabi is about 1750 BC. - is actually a table of what we now call the Pythagorean triples .
Well, this Babylonian knowledge has been lost to humanity for almost 3,000 years. And instead, schemes based on natural languages were used, with separate characters for ten, one hundred, and so on.
So, for example, the Egyptians used the symbol of a lotus flower to denote a thousand, for a hundred thousand - a bird, and so on. Each power of ten for its designation had a separate symbol.
And then another very important idea came up that neither the Babylonians nor the Egyptians thought of. It consisted of denoting numbers by numbers - that is, not denoting a number by seven by seven units of something, but by only one symbol.
However, among the Greeks, perhaps, as with the Phoenicians, this idea already existed. Well, actually, she was a little different. It consisted in denoting a sequence of numbers through a sequence of letters in their alphabet. That is, alpha corresponded to one, beta to two, and so on.
Here is the list of numbers in the Greek notation [you can download the Wolfram Language Package, which allows you to represent numbers in various ancient notations here - approx. Ed.].
(I think that is how the system administrators from the Plato Academy would adapt their version of Mathematica ; their imaginary -600th (or so) version of Mathematica .)
There are a lot of problems with this number system. For example, there is a serious version control problem: even if you decide to remove some letters from your alphabet, you must leave them in numbers, otherwise all your previously written numbers will be incorrect.
That is, this means that there are various outdated Greek letters that remain in the number system - like coppa for the number 90 and sampi for the number 900. However, I included them in the character set for Mathematica , because the Greek form of writing numbers works fine here.
After some time, the Romans developed their own notation of numbers, which we are familiar with.
Let it be now and it is not clear that their numbers were originally thought of as letters, but this should be remembered.
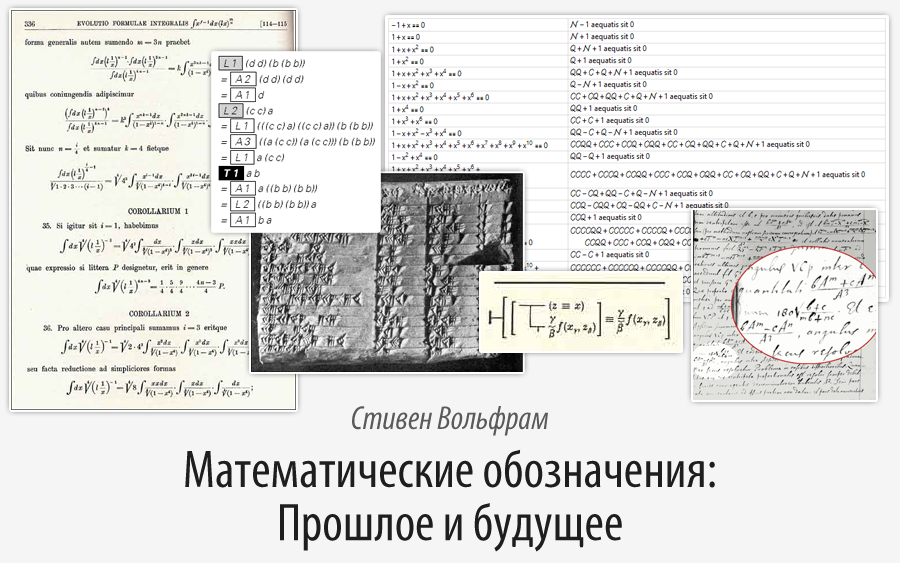
So, let's try the Roman form of writing numbers.
This is also a rather inconvenient way to write, especially for large numbers.
There are some interesting points. For example, the length of the represented number recursively increases with the size of the number.
And in general, such a representation for large numbers is full of unpleasant moments. For example, when Archimedes wrote his work on the number of grains of sand, the volume of which is equivalent to the volume of the universe (Archimedes estimated their number at 10 51 , however, I believe that the correct answer will be about 10 90 ), then he used ordinary words instead of notation to describe such a large number.
But in fact there is a more serious conceptual problem with the idea of representing numbers as letters: it becomes difficult to come up with a representation of symbolic variables - some kind of symbolic objects that numbers are behind . Because any letter that could be used for this symbolic object can be confused with a digit or a fragment of a number.
The general idea of the symbolic designation of some objects through letters has been known for quite some time. Euclid, in fact, used this idea in his work on geometry.
Unfortunately, the original works of Euclid were not preserved. However, there are several hundred years younger versions of his work. Here is one written in Greek.
And on these geometric figures you can see points that have a symbolic representation in the form of Greek letters. And in the description of theorems there are many points at which points, lines and angles have a symbolic representation in the form of letters. So the idea of a symbolic representation of some objects in the form of letters originates at least from Euclid.
However, this idea may have appeared earlier. If I could read Babylonian, I could probably tell you for sure. Here is the Babylonian tablet, which represents the square root of the two, and which uses the Babylonian letters for designation.
I believe that burnt clay is more durable than papyrus, and it turns out that we know more about what the Babylonians wrote than about what people like Euclid wrote.
In general, this inability to see the ability to enter names for numeric variables is an interesting case when languages or notation limit our thinking. This is what undoubtedly is discussed in ordinary linguistics. In the most common wording, this idea sounds like the Sapir-Whorf hypothesis (the linguistic relativity hypothesis).
Of course, for those of us who have spent some of our lives developing computer languages, this idea seems very important. That is, I know for sure that if I think in Mathematica , many concepts will be simple enough for me to understand, and they will not be at all so simple if I think in some other language.
But, in any case, without variables everything would be much more complicated. For example, how do you imagine a polynomial?
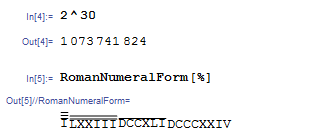
Well, Diophantus - the very one who came up with Diophantine equations - was faced with the problem of representing polynomials in the middle of the 2nd century A.D. In the end, he came up with the use of certain letter-based names for squares, cubes, and more. Here's how it worked.
At least right now it would seem extremely difficult for us to understand the notation of Diophantus for polynomials. This is an example of not very good notation. I believe that the main reason, in addition to limited extensibility, is that these notations make the mathematical connections between polynomials non-obvious and do not highlight the most interesting points for us.
There are other schemes for defining polynomials without variables, such as the Chinese scheme , which included the creation of a two-dimensional array of coefficients.
The problem here, again, is extensibility. And this problem with graph-based notations pops up again and again: a piece of paper, papyrus or whatever - they are all limited to two dimensions.
OK, so what about the letter designation of variables?
I believe that they could appear only after the appearance of something similar to our modern notation. And she did not appear until a certain time. There were some hints in the Indo-Arabic designations in the middle of the first millennium, but everything was established only towards its end. And to the west this idea came only with Fibonacci work on computing in the 13th century.
Fibonacci, of course, was the one who talked about Fibonacci numbers in relation to the problem of rabbits, but in reality these numbers have been known for more than a thousand years, and they served to describe the forms of Indian poetry. And I always found the case with Fibonacci numbers an amazing and sobering episode in the history of mathematics: having arisen at the dawn of Western mathematics, so familiar and fundamental, they began to become popular only in the 80s.
In any case, it is also interesting to note that the idea of breaking up numbers into groups of three in order to make large numbers more readable is already in the Fibonacci book of 1202, although I think that he talked about using brackets over numbers, and not about separating commas .
After Fibonacci, our modern presentation for numbers is gradually becoming more popular, and by the time printing began in the 15th century, it was already universal, although there were still some wonderful moments.
But algebraic variables in their full sense did not exist then. They appeared only after Viet at the end of the 16th century and gained popularity only in the 17th century. That is, Copernicus and his contemporaries did not have them yet. As basically with Kepler. These scientists used plain text, sometimes structured like Euclid’s, to describe some mathematical concepts.
By the way, even though the mathematical notation in those days was not very well developed, the system of symbolic notation in alchemy, astrology and music were quite developed. So, for example, Kepler at the beginning of the 17th century used something similar to modern musical notation, explaining his “music of the spheres” for the relations of planetary orbits.
Since Vietnam, letter designations for variables have become commonplace. Usually, by the way, he used vowels for the unknown and consonants for the famous.
This is how Viet wrote polynomials in a form that he called " zetetics ", and now we would call it just symbolic algebra :
You can see that he uses words to mean operations, mainly so that they cannot be confused with variables.
Since operations were previously presented, in what form?
The idea that operations are something that can be imagined in some form has been getting to people's minds for quite some time. The Babylonians usually did not use symbols for operations - for addition they simply wrote down the terms one after another. And in general, they were predisposed to write everything in the form of tables, so that they did not need to somehow denote operations.
The Egyptians had some designations for operations: for addition, they used a pair of legs walking forward, and for subtraction, they went backwards.
And the modern + sign , which is probably an abbreviation of " et " in Latin (means "and"), appeared only at the end of the 15th century.
And here is something from 1579 that looks very modern, written mainly in English, until you begin to understand that those funny squiggles are not Xs, but special non-letter characters that represent different degrees for variables.
In the first half of the 17th century, a kind of revolution took place in mathematical notation, after which it practically gained its modern form. A modern square root designation was created, which was previously designated as Rx - this designation is now used in medical prescriptions. And basically algebraic notation has acquired its modern form.
William Otred was one of those people who seriously dealt with this issue. The invention of the slide rule- one of the things that made him famous. In fact, almost nothing is known about him. He was not a major mathematician, but he did a lot of useful teaching, with people like Christopher Wren and his students. It is strange that I did not hear anything about him at school, especially when you consider that we studied at the same school, only he was 400 years earlier. However, the invention of the slide rule was not enough to perpetuate its name in the history of mathematics.
But, in any case, he was seriously engaged in notation. He came up with a cross to denote multiplication, and he advanced the idea of representing algebra through notation instead of words - just like Viet did. And, in fact, he invented quite a few other notations, like a tilde for predicates like IntegerQ .
After Otred and his associates, these designations quickly established. There were alternative notations, like images of a waning and growing moons to denote arithmetic operations - a fine example of a poor and non-expandable design. However, modern designations were mainly used.
Here is an example.
This is a fragment of Newton’s manuscript Principia , from which it is clear that he mainly used modern algebraic notation. I think it was Newton who came up with the use of negative powers instead of fractions for reciprocal values and other things. Principleiacontains very few notations, with the exception of these algebraic things and representations of various material in the style of Euclid. And in fact, Newton was not particularly interested in notation. He even wanted to use point designations for his fluxes.
What can not be said about Leibniz. Leibniz paid much attention to questions of notation. In fact, he believed that the correct notation is the key to many human issues. He was a kind of diplomatic analyst, plying between different countries, with all their different languages, etc. He had the idea that if you create some kind of universal logical language , then all people would be able to understand each other and would have the opportunity to explain anything.
There were other people who thought about this, mainly from the standpoint of ordinary natural languages and logic. One example is a rather specific character named Raymond Lul, who lived in the 14th century, who claimed to have invented some logical wheels that provide answers to all the questions of the world.
But one way or another, Leibniz developed those things that were interesting from the point of view of mathematics. What he wanted to do was one way or another to combine all kinds of notation in mathematics into some exact natural language with a mathematics-like way of describing and solving various problems, or even more - to combine all the natural languages used.
Well, like many of his other projects, Leibniz never realized this. However, he was engaged in various fields of mathematics and was serious about developing notation for them. His most famous designations were introduced by him in 1675. To use the integrals, he used " omn. ", Possibly as a shorthand for omnium . But on Friday, October 29, 1675, he wrote the following.
On this piece of paper you can see the sign of the integral. He conceived it as extended the S . Undoubtedly, this is the modern designation of the integral. Well, there is almost no difference between the notation of integrals then and now.
Then on Thursday November 11 of that year, he designated the differential as " d". In fact, Leibniz considered this designation not the best and planned to come up with some kind of replacement for him. But, as we all know, this did not happen.
Well, Leibniz corresponded on the designations with a variety of people. He saw himself by whom something like the chairman of the committee of standards for mathematical notation - so we would say now. He believed that the notation should be as brief as possible. For example, Leibniz said: " Why use two points to indicate division, when you can use only one? ".
Some of the ideas he promoted were never received. For example, using letters to denote variables, he used astronomical signs to denote expressions. Quite an interesting idea, actually.
So he designated functions.
In addition to these points and some exceptions, like the symbol of the intersection of squares, which Leibniz used to denote equality, its notation has remained practically unchanged to this day.
In the 18th century Euler actively used notation. However, in fact, he followed the path of Leibniz. I believe he was the first to seriously use Greek letters along with Latin letters to indicate variables.
There are some other designations that appeared shortly after Leibniz. The following is an example from a book published several years after Newton's death. This is a textbook of algebra, and it contains very traditional algebraic notation, already in print.
And here is Lapital's book, printed at about the same time, in which almost modern algebraic notation is already in place.
And finally, here is an example from Euler, containing very modern notation for integrals and other things.
Euler - popularized the modern designation for the number pi , which was originally proposed by William Jones, who saw it as an abbreviation for the word perimeter.
The notation proposed by Leibniz and associates for quite some time remained unchanged. Small changes occurred, for example, the square xx received the spelling x 2 . However, practically nothing new has appeared.
However, at the end of the 19th century, a new surge of interest in mathematical notation was observed, coupled with the development of mathematical logic. There were some innovations made by physicists such as Maxwell and Gibbs, mainly for vectors and vector analysis, as a consequence of the development of abstract algebra . However, the most significant changes were made by people, starting with Frege and from about 1879, who were engaged in mathematical logic.
These people in their aspirations were close to Leibniz. They wanted to develop a notation that would represent not only mathematical formulas, but also mathematical conclusions and proofs. In the mid-19th century, Boole showed that the foundations of propositional logic can be represented in terms of mathematics. However, Frege and his like-minded people wanted to go further and present both the propositional logic and any mathematical judgments in the corresponding mathematical terms and notation.
Frege decided that graphic designations would be required to solve this problem. Here is a fragment of his so-called " conceptual notation ."
Unfortunately, it is difficult to understand. And in fact, if you look at the history of signs in general, you can often find attempts to invent graphic signs that turned out to be difficult to understand. But in any case, Frege's designations certainly did not become popular.
Then there was Peano, the main enthusiast in the field of mathematical notation. He relied on a linear representation of notation. Here's an example:
Generally speaking, in the 80s of the 19th century, Peano developed what is very close to the notation used in most modern set-theoretic concepts.
However, like Leibniz, Peano did not want to dwell only on the universal notation for mathematics. He wanted to develop a universal language for everything. This idea was realized in him in what he calledinterlingua is a language based on simplified Latin. Then he wrote something like a brief summary of mathematics, calling it Formulario Mathematico , which was based on his notation for formulas, and this work was written on this derivative from Latin - on interlingua.
Interlingua, like Esperanto, which appeared around the same time, was not widely used. However, this cannot be said of Peano's notation. At first, nobody really heard anything about them. But then Whitehead and Russell wrote their Principia Mathematica , which used Peano's notation.
I think Whitehead and Russell would have won a prize in the nomination "the most mathematical-saturated work that has ever been done without the help of computing devices . "Here is an example of a typical page from Principia Mathematica .
They had every conceivable kind of notation. A frequent story when authors ahead of their publishers: Russell himself designed fonts for many used signs them .
and, of course, then it was not on TrueType fonts or Type 1, and most of these pieces of lead. I mean, that Russell could be met with a cart full of lead impressions, rolling it into a publishing Cambrian zhskogo University to ensure the correct layout of his books.
But, despite all these efforts, the results were rather grotesque and obscure. I think it's pretty clear that Russell and Whitehead have gone too far with their notation.
Although the area of mathematical logic has become a little clearer as a result of the activities of Russell and Whitehead, it still remains the least standardized and contains the most complex notation.
But what about the more common math components?
For a while at the beginning of the 20th century, what was done in mathematical logic has not yet produced any effect. However, the situation began to change dramatically with the Bourbaki movement , which began to expand in France in the approximately forties.
Bourbaki emphasized a much more abstract, logical-oriented approach to mathematics. In particular, they focused on the use of notation wherever possible, in any way minimizing the use of potentially inaccurate text.
Somewhere since the forties, work in the field of pure mathematics has undergone serious changes, which can be seen in the relevant journals, in the works of the international mathematical community and other sources of this kind. The changes consisted of a transition from works full of text and only with basic algebraic and computational calculations to works saturated with notation.
Of course, this trend did not affect all areas of mathematics. This is in some ways what linguistics of ordinary natural languages do. From the obsolete mathematical notation used, you can see how the various areas that use them lag behind the main highway of mathematical development. So, for example, we can say that physics remained somewhere at the end of the 19th century, using the already obsolete mathematical notation of those times.
There is one point that is constantly manifested in this area - notation, like ordinary languages, strongly separates people. I mean, there is a big barrier between those who understand specific designations and those who do not understand. This seems rather mystical, reminiscent of the situation with alchemists and occultists - mathematical notation is full of signs and symbols that people in everyday life do not use, and most people do not understand them.
In fact, it is rather curious that recently a trend has appeared in advertising on the use of mathematical notation. I think, for some reason, mathematical notation has become a bit of a chic. Here is one relevant example of advertising.
The attitude to mathematical notation, for example, in school education, often reminds me of the attitude to symbols of secret communities and the like.
Well, this was a brief summary of some of the most important episodes in the history of mathematical notation.
In the course of historical processes, some designations have ceased to be used. Besides some areas, such as mathematical logic, it has become very standardized. The difference in the designations used by different people is minimal. As with any ordinary language, math records almost always look the same.
Computers
The question is: can computers be made to understand these notations?
It depends on how systematized they are and how much meaning can be extracted from some given fragment of the mathematical notation.
Well, I hope I managed to convey the idea that the notation developed as a result of ill-conceived random historical processes. There were several people, such as Leibniz and Peano, who tried to approach this issue more systematically. But basically designations appeared in the course of solving specific problems - similar to how it happens in ordinary spoken languages.
And one of the things that surprised me was that, in fact, there was never an introspective study of the structure of mathematical notation .
The grammar of ordinary spoken languages has evolved over the centuries. Without a doubt, many Roman and Greek philosophers and speakers paid her much attention. And, in fact, as early as about 500 BC. e. Panini amazingly detailed and clearly painted the grammar for Sanskrit. In fact, Panini's grammar was surprisingly similar in structure to the specification of the rules for creating computer languages in the form of Backus-Naur , which is currently used.
And there were grammars not only for languages - in the last century an endless number of scientific papers on the correct use of the language and the like have appeared.
But, despite all this activity in relation to ordinary languages, in fact, absolutely nothing was done for the language of mathematics and mathematical notation. This is really pretty weird.
There were even mathematicians who worked on grammars of ordinary languages. An early example was John Wallis, who coined the Wallis product formula for pi, and now he wrote English grammar in 1658. Wallis was the same person who started all this turmoil with the correct use of " will " or " shall ".
At the beginning of the 20th century, mathematical logic talked about different layers of a correctly formed mathematical expression: variables inside functions inside predicates inside functions inside connecting words inside quantifiers . But not about what all this meant for the designations of expressions.
Some certainty appeared in the 50s of the 20th century, when Chomsky and Bakus independently developed the ideacontext-free languages . The idea came to work on the rules of substitution in mathematical logic, mainly thanks to Emil Post in the 20s of the 20th century. But, it is curious that both Chomsky and Bakus had the same idea precisely in the 1950s.
Bakus applied it to computer languages: first to Fortran , then to ALGOL . And he noticed that algebraic expressions can be represented in context-free grammar.
Chomsky applied this idea to ordinary human language. And he noted that, with some degree of accuracy, ordinary human languages can also be represented by context-free grammars .
Of course, linguists, including Chomsky, spent years demonstrating how nevertheless this idea was untrue. But the thing that I have always noted, and from a scientific point of view, I considered the most important, is that in the first approximation this is still the truth - that ordinary natural languages are context-free .
So, Chomsky studied ordinary language, and Bakus studied things like ALGOL. However, none of them considered the issue of developing more advanced mathematics than a simple algebraic language. And, as far as I can tell, almost no one has dealt with this issue since then.
But, if you want to see if you can interpret some mathematical notation, you need to know what type of grammar they use.
Now I must tell you that I considered the mathematical notation something too random for the computer to correctly interpret it. In the early nineties, we were burning with the idea of allowing Mathematica to work with mathematical notation. And in the process of implementing this idea, we had to figure out what is happening with mathematical notation.
Neil Soiffer spent many years working on editing and interpreting mathematical notation, and when he joined us in 1991, he was trying to convince me that mathematical notation could work - both input and output.
The data output part was quite simple: in the end, TROFF and TEX have already done a great job in this direction.
The question was data entry.
In fact, we have already found out something for ourselves regarding the conclusion. We realized that at least at some level, many mathematical notations can be represented in some context-free form. Since many people know a similar principle from, say, TEX, it would be possible to configure everything through work with nested structures.
But what about the input? One of the most important points was what is always encountered when parsing: if you have a line of text with operators and operands, then how to specify what is grouped and what?
So let's say you have a similar mathematical expression.
Sin [x + 1] ^ 2 + ArcSin [x + 1] + c (x + 1) + f [x + 1]
What does it mean? To understand this, you need to know the priorities of the operators - which are stronger and which are weaker with respect to operands.
I suspected that there was no serious justification for this in any articles devoted to mathematics. And I decided to research it. I went through a wide variety of mathematical literature, showed different people some random fragments of mathematical notation and asked them how they would interpret them. And I found a very interesting thing: there was an amazing coherence of people's opinions in determining the priorities of operators . Thus, it can be argued: there is a certain sequence of priorities for mathematical operators .
It can be said with some certainty that people represent precisely this sequence of priorities when they look at fragments of mathematical notation.
Having discovered this fact, I became much more optimistic about the possibility of interpreting the mathematical notation introduced. One of the ways you can always implement this is to use templates . That is, it is enough just to have a template for the integral and fill in the cells of the integrand, variable and so on. And when the template is inserted into the document, then everything looks as it should, however, it still contains information about what kind of template it is, and the program understands how to interpret it. And many programs really do.
But overall, this is extremely inconvenient. Because if you try to quickly enter data or edit, you will find that the computer is beeping and does not allow you to do those things that, obviously, should be available to you for implementation.
Giving people the ability to enter in free form is a much more difficult task . But this is what we want to implement.
So what does this entail?
First of all, the mathematical syntax must be carefully thought out and unambiguous. Obviously, you can get a similar syntax if you use a common programming language with line-based syntax. But then you will not get the familiar mathematical notation.
Here is the key problem: traditional mathematical notation contains ambiguities. At least if you want to present it in a fairly general way. Take, for example, " i ". What is it - Sqrt [-1] or the variable " i "?
In a regular text InputForm in Mathematica, all such ambiguities are resolved in a simple way: all built-in Mathematica objects begin with a capital letter .
But the capital “ I ” is not very similar to what Sqrt [-1] is indicated in mathematical texts. And what to do with it? And here is the key idea: you can make another character, which also seems to be a capital “ i ”, but it will not be a regular capital “ i", And the square root of -1 .
One might think: Well, why not just use two “ i ” that look the same - just like in mathematical texts - but will it be special from them? Well, that would definitely be confusing. You will need to know which “ i ” you are typing, and if you move it somewhere or do something like that, you will get confusion.
So, then there must be two " i ". What should the special version of this symbol look like?
We had an idea - to use double tracing for a symbol. We tried a variety of graphical representations. But the double-drawn idea turned out to be the best. In a way, it meets the tradition in mathematics to designate specific objects with a double mark.
So, for example, capital R could be a variable in mathematical records. But R with double tracing is already a specific object, which denotes a set of real numbers.
So the double-drawn “ i ” is a specific object that we call ImaginaryI . Here's how it works:
The idea of double-drawing solves many problems.
Including the largest - integrals. Suppose you are trying to develop syntax for integrals. One of the key questions is what can the d mean in the integral? What if it is a parameter in the integrand? Or a variable? It turns out terrible confusion.
Everything becomes very simple if you use DifferentialD or " d " with double-drawing. And you get a well-defined syntax.
You can integrate x to the power of d divided by the square root of x + 1 . Here's how it works:
It turns out that only a few small changes are required in the basis of the mathematical notation in order to make it unambiguous. It is surprising. And very cool. Because you can simply enter something, consisting of mathematical notation, in a free form, and it will be perfectly understood by the system. And this is what we implemented in Mathematica 3.
Of course, for everything to work as it should, you need to deal with some nuances. For example, to be able to enter anything that is effective and easy to remember. We thought about this for a long time. And we came up with some good and general schemes for implementing this.
One of them is entering things like degrees as superscripts. In normal text input, the symbol is used to indicate the degree^ . The idea is to use control - ^ with which you can enter an explicit superscript. The same idea for the combination control - / , with which you can enter a "two-story" fraction.
Having a clear set of principles like this is important in order to get everyone to work together in practice. And it works. Here is what the input of a rather complicated expression might look like:
But we can take fragments from this result and work with them.
And the point is that this expression is completely clear to Mathematica , that is, it can be calculated. It follows that the execution results ( Out ) are objects of the same nature as the input data ( In), that is, they can be edited, parts of them can be used separately, fragments of them can be used as input, and so on.
To make all this work, we had to generalize common programming languages and analyze something. Previously, the opportunity was introduced to work with a whole "zoo" of special characters as operators. However, perhaps more importantly, we have implemented support for two-dimensional structures. So, in addition to prefix operators, there is support for overfix operators and more.
If you look at this expression, you can say that it does not quite resemble traditional mathematical notation. But it is very close. And it undoubtedly contains all the features of the structure and recording forms of ordinary mathematical notation. And the important thing is that no one who has the usual mathematical notation will have difficulties in interpreting this expression.
Of course, there are some cosmetic differences from what could be seen in a regular math textbook. For example, how trigonometric functions are written, and so on.
However, I bet that StandardForm in Mathematicabetter and clearer to represent this expression. And in a book that I wrote for many years about a scientific project that I was engaged in, I used only StandardForm to represent anything .
However, if full compliance with ordinary textbooks is needed, then something else will be needed. And here is another important idea implemented in Mathematica 3: to separate StandardForm and TraditionalForm .
Any expression I can always convert to TraditionalForm .
And in fact, TraditionalForm always contains enough information to be uniquely converted back to StandardForm.
But TraditionalForm looks almost like ordinary mathematical notation. With all of these rather strange things in traditional mathematical notation, like writing a sine squared x instead of a sine x squared and so on.
So what about entering TraditionalForm?
You may have noticed a dotted line to the right of the cell [in the other pins of the cell were hidden to simplify the pictures - approx. Ed.]. They mean that there is some dangerous moment. However, let's try to edit something.
We can perfectly edit everything. Let's see what happens if we try to figure it out.
There is a warning. In any case, we continue anyway.
Well, the system understood what we want.
In fact, we have several hundred heuristic rules for interpreting expressions in traditional form. And they work quite well. Good enough to go through the large volumes of obsolete mathematical notations defined, say, in TEX, and automatically and unambiguously convert them to meaningful data in Mathematica .
And this opportunity is very inspiring. Because for the same obsolete natural language text, there is no way to convert it into something meaningful. However, in mathematics there is such an opportunity.
Of course, there are some things related to mathematics, mainly on the output side, with which there are substantially more difficulties than with plain text. Part of the problem is that mathematics is often expected to work automatically. You can not automatically generate a lot of text, which will be meaningful enough. However, in mathematics, calculations are performed that can produce large expressions.
So you need to figure out how to break the expression into lines so that everything looks neat enough, and in Mathematica we did a good job on this task. And several interesting questions are connected with it, such as, for example, that while editing an expression, the optimal line break can constantly change as you work.
And this means that there will be such nasty moments, as if you are typing, and suddenly the cursor jumps back. Well, I think we solved this problem in a rather elegant way. Let's look at an example.
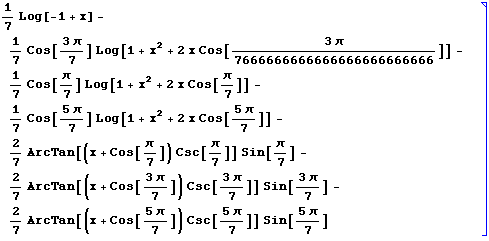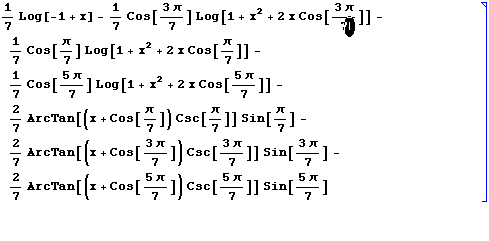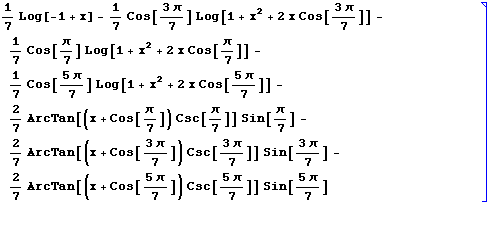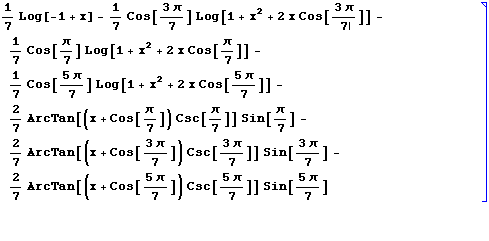
Did you see it? There was a funny animation that appears for a moment when the cursor should move back. You may have noticed her. However, if you were typing, you probably would not have noticed that the cursor moved back, although you could have noticed it, because this animation makes your eyes automatically look at this place. From the point of view of physiology, I believe that this works due to nerve impulses that do not enter the visual cortex, but directly into the brain stem, which controls eye movements. So, this animation makes you subconsciously move your gaze to the right place.
Thus, we were able to find a way to interpret standard mathematical notation. Does this mean that now all work in Mathematica should now be carried out in the framework of traditional mathematical notation? Should we introduce special characters for all operations presented in Mathematica ? This way you can get a very compact notation. But how reasonable is that? Will it be readable?
Perhaps the answer is no.
I think that here lies a fundamental principle: someone wants to represent everything in the notation, and not use anything else .
And someone does not need special designations. And someone uses Mathematica FullForm. However, it is very tiring to work with this form. Perhaps that is why language syntax like LISP seems so difficult - in fact, it is the FullForm syntax in Mathematica .
Another possibility is that everything can be assigned special designations. It will turn out something like APL or some fragments of mathematical logic. Here is an example of this.
Pretty hard to read.
Here is another example from the original Turing article, which contains the notation for the universal Turing machine, again - an example of not the best notation.
It is also relatively unreadable.
The question is what lies between two extremes such as LISP and APL. I think this problem is very close to the one that occurred when using very short names for teams.
For example, Unix. Earlier versions of Unix looked pretty cool when there was a small amount of short ones for a set of commands. But the system was expanding. And after some time there was already a large number of teams consisting of a small number of characters. And most ordinary mortals could not remember them. And everything began to look completely incomprehensible.
The same situation as with mathematical or other notation, for that matter. People can only work with a small number of special forms and characters. Perhaps with a few dozen. Commensurate with the length of the alphabet. But not more. And if you give them more, especially all at once, they will have complete confusion in their heads.
This should be a little specific. Here, for example, are many different relationship operators.
But most of them essentially consist of a small number of elements, so there should not be a problem with them.
Of course, in principle, people can learn a very large number of characters. Because in languages like Chinese or Japanese, there are thousands of hieroglyphs. However, people need a few extra years to learn to read in these languages compared to those using the regular alphabet.
If we talk about symbols, by the way, I think that it’s much easier for people to cope with some new symbols as variables than as operators. And it is very interesting to consider this issue from the point of view of history.
One of the most interesting points - at all times and almost without exception, only Latin and Greek characters were used as variables. Well, Cantor introduced Alephtaken from Hebrew for their cardinal numbers of infinite sets. And some people claim that the symbol of the partial derivative is the Russian q , although I think that this is actually not the case. However, there are no other characters that would be borrowed from other languages and gained distribution.
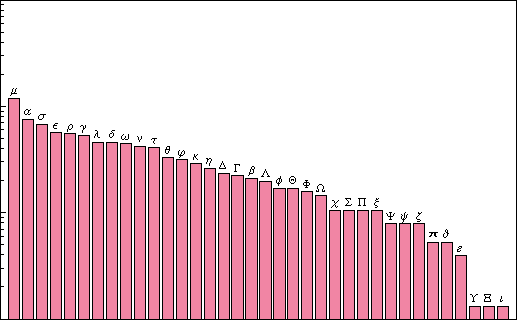
By the way, you probably know that in English the letter " e " is the most popular, then comes " t ", and so on. And I was curious about the distribution of the frequency of use of letters in mathematics. Because I explored the MathWorld site, which contains a large amount of mathematical information - more than 13,500 entries, and looked at the distribution for the various letters [unfortunately, this picture taken by Stephen could not be modernized - approx. Ed.].
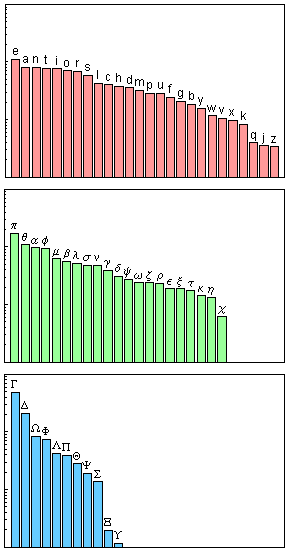
You can see that " e " is the most popular. And it is very strange that " a " takes second place. It is very unusual. You can see that the lowercase π is the most popular, followed by θ, α, φ, μ, β and so on. And among the capital ones, the most popular are Γ and Δ.
Good. I talked a little about the notation, which in principle can be used in mathematics. So which notation is best for use?
Most people using mathematical notation have probably asked this question. However, for mathematics there is no analogue similar to Fowler's " Modern Use of English " for English. There was a small book called Mathematics in Print , published by AMS, but it was mainly about printing techniques.
As a result, we do not have well-written principles similar to things like infinitives with individual particles in the English language.
If you use StandardForm in Mathematica , you no longer need it. Because everything that you enter will be unambiguously interpreted. However, for TraditionalForm, some principles should be followed. For example, do not write
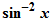, because it is not clear what this means.Future
To finish, let me tell you a little about the future of mathematical notation.
What, for example, should a new notation be?
A character book will contain about 2,500 characters that are popular in certain areas and are not letters of languages. And with the correct spelling of characters, many of them could ideally be combined with mathematical symbols.
Why use them?
The first opportunity that comes to mind is notation for representing programs and mathematical operations. In Mathematica, for example, quite a lot of text operators are used in programs. And I thought for a long time that it would be great to be able to use some special characters for them instead of combinations of ordinary ASCII characters [recent versions of Mathematica fully support Unicode - approx. Ed.].
It turns out that sometimes this can be implemented very simply. Since we chose ASCII characters, it is often possible to get some characters that are very close in spelling, but more elegant. For example, if you type -> in Mathematica , then this arrow will automatically turn into a more elegant one . And all this is possible due to the fact that the parser in Mathematica
can work with special characters as well. I often thought about how to expand all this. And so, new ideas are gradually emerging. Pay attention to the pound sign # , or the license plate, or, as it is sometimes called, the octotorp, which we use in those places where the parameter of the pure function is passed. It resembles a square with tentacles. And in the future, perhaps, it will be denoted by a nice square with small serifs, and will mean a place for passing a parameter to a function. And it will be smoother, not like a piece of regular code, something like an icon.
How far can one go in this direction - representing things in visual form or in the form of pictograms? It is clear that such things as flowcharts in engineering, commutative diagrams in pure mathematics, and technological diagrams all cope well with their tasks. At least until now. But how long can this go on?
I don’t think so for a very long time. I think some come close to some fundamental limitations of people in the processing of linguistic information.
When languages are more or less context-free, have a tree structure, much can be done with them. Our buffer memory consists of five memory elements and, whatever it is, it will be able to easily parse them. Of course, if we have too many supporting sentences, even in a context-free language, then there will be a chance to run out of stack space and get into trouble. But, if the stack does not go too deep, then everything will work as it should.
But what about networks? Can we understand arbitrary networks? I mean - why should we only have prefix, infix, overfix operators? Why don't operators get their arguments through some kind of connection within the network?
I was particularly interested in this issue in the context of the fact that I was involved in some scientific issues regarding networks. And I really would like to get some language representation for networks. But despite the fact that I devoted a lot of time to this issue, I don’t think that my brain could work with similar networks in the same way as with ordinary language or mathematical constructions that have a one-dimensional or two-dimensional context-free structure. So I think this is probably the place that the notation cannot reach.
In general, as I mentioned above, this is a frequent case when language or notation limits our space of the imaginable.
So what does this mean for math?
In my research project, I developed some basic generalizations of what people usually relate to mathematics. And the question is, which designations can be used for the abstract representation of such things.
Well, I have not yet been able to fully answer this question. However, I found that, at least in most cases, the graphical representation or the representation in the form of pictograms is much more effective than the notation in the form of constructions in ordinary languages.
Returning to the very beginning of this conversation, the situation resembles what has happened for thousands of years in geometry. In geometry, we know how to represent something graphically. Since the days of ancient Babylon. And a little over a hundred years ago, it became clear how to formulate geometric problems from the point of view of algebra.
However, we still do not know a simple and clear way to represent geometric patterns in notation in natural language. And my guess is that almost all of these mathematical things can be represented only in small numbers in natural language notation.
However, we humans only perceive these designations in natural language easily. So we tend to learn things that can be represented in this way. Of course, such things cannot be what happens in nature and the universe.
But this is a completely different story. So I'd better end with that.
Many thanks.
Notes
During the discussion after the speech and during communication with other people at the conference, several points arose that should be discussed.
Empirical laws for mathematical notation
In the study of ordinary natural language, various historical and empirical laws were discovered. An example is Grimm's Law , which describes consonantal translations in Indo-European languages. I was curious if such historical-empirical laws could be found for mathematical notation.
Dana Scott suggested this option: a tendency to remove explicit parameters .
As an example, in the 60s of the 19th century, often each component of the vector was named separately. But then the components began to be marked with indices - as a i . And shortly afterwards - mainly after Gibbs' work - vectors began to represent as one object, denoted, say, as
or a .With tensors, everything is not so simple. A notation that avoids explicit indices is usually called coordinate-free . And such a notation is a frequent occurrence in pure mathematics. However, in physics, this approach is considered too abstract, because explicit indices are used everywhere.
With respect to functions, there is also a tendency not to explicitly mention parameters. In pure mathematics, when functions are considered through comparisons, they are often mentioned only by their name - simply f , without any parameters.
However, this will be good only when the function has only one parameter. When there are several parameters, it usually becomes unclear how those data streams that are associated with the parameters will work.
However, as early as the 1920s, it was shown that so-called combinators can be used to define such data streams without any explicit indication of the parameters.
Combinators were not used in the mainstream mathematics, however, from time to time they became popular in computational theory, although their popularity was noticeably reduced due to incompatibility with the idea of data types.
Combinators are fairly easy to set in Mathematica by defining a function with a compound header. Here's how to define standard combinators:
k [x _] [y _]: = ix
s [x _] [y _] [z _]: = x [z] [y [z]]
If you define an integer n , in fact, in unary system using Nest [s [s [k [s]] [k]], k [s [k] [k]], n]then addition can be defined as s [k [s]] [s [k [s [k [s]]]] [s [k [k]]]] , multiplication as s [k [s]] [ k] , and the degree is s [k [s [s [k] [k]]]] [k] . No variables are required.
The problem is that the expressions are incomprehensible, and there is nothing to be done about it. I tried to find some ways to more clearly represent them and their calculations. I have made little progress, but I cannot say that the problem has been solved.
Printed versus Screen
Some asked about the difference in print and screen design capabilities.
In order to understand the notation, they must be similar, and the difference between them should not be very large.
But there are some obvious possibilities.
Firstly, the screen can easily use color. One would think that it was somehow convenient to use different colors for variables. My experience suggests that this is convenient for clarifying the formula. However, everything will become very confusing if, for example, different variables correspond to red x and green x .
Another possibility is to have some animated elements in the formula. I believe that they will be as annoying as the blinking text, and will not be particularly useful.
Perhaps the better idea is to be able to hide and expand certain parts of the expression - like groups of cells in a Mathematica laptop . Then it will be possible to immediately get an idea of the whole expression, and if the details are interesting, then expand it further and further.
Written notation
Some would have thought that I had devoted too much time to graphic notation.
I would like to clarify that I find the graphical notation of ordinary mathematical operations and operations rather difficult. In my book A New Kind of Science, I use graphics everywhere, and I don’t think of any other way to do what I do.
Both in traditional science and in mathematics there are many graphic notations that work great, albeit mainly for static designs.
Graph theory is an obvious example of using graphical representation.
Structural diagrams from chemistry and Feynman diagrams from physics are close to them.
In mathematics, there are methods for group theoretical calculations, presented in part thanks to Predrag Zwitanowicz, and now they are based on a graphical notation.
And in linguistics, for example, diagrams for sentences are common, showing a tree of linguistic components and ways of grouping them to form sentences.
All these designations, however, become of little use in cases of investigation of some very large objects. However, Feynman diagrams typically use two loops, and five loops are the maximum for which explicit general calculations have ever been made.
Fonts and Symbols
I promised to tell you something about symbols and fonts.
In Mathematica 3, we had to do a lot of work to develop fonts for more than 1,100 characters related to mathematical and technical notation.
Getting the right shape - even for Greek letters - was often quite complicated. On the one hand, we wanted to preserve some tradition in writing, and on the other hand, to make Greek letters as unlike the English as possible and whatever.
In the end, I made sketches for most characters. This is what we have come to in Greek letters. We designed the Times-like font, a monospaced font like Courier, and now we are developing sans serif. Designing a Courier font was no easy task. For example, it was necessary to figure out how to make the iota occupy the entire slot for the symbol.
There were also difficulties with script and gothic (textured) fonts. Often in these fonts, the letters are so unlike ordinary English that they become completely unreadable. We wanted these fonts to fit in with their theme, and still have the same dimensions as regular English letters.
Here's what we got:
The website fonts.wolfram.com, which contains all the detailed information about symbols and fonts, of course, if they are related to Mathematica and its fonts.
Search for mathematical formulas
Some people asked about the search for mathematical formulas [after creating Wolfram | Alpha, a huge amount of databases appeared in the Wolfram Language language, now you can get a huge array of information about any formulas using the MathematicalFunctionData function - approx. Ed.].
Obviously, it’s easy to say what a plain text search is. The only question is the equivalence of lowercase and uppercase letters.
For mathematical formulas, everything is more complicated because there are still many different equivalences. If you ask about all possible equivalences, then everything will become too complicated. But if you ask about equivalences that simply mean replacing one variable with another, you can always determine whether two expressions are equivalent.
However, this will require the power of the detector of the same Mathematica patterns .
We plan to embed the ability to search for formulas in our functions.wolfram.com website , but here I will not dwell on the details.
Non-visual designations
Someone asked about non-visual designations.
The first thought that I had was that human vision provides much more information than, say, hearing. In the end, our eyes connected with millions of nerve endings, and with the ears only 50 000.
In Mathematica built-in ability to generate sound from the second version, which was released in 1991. And there were some moments when this function turned out to be useful for understanding some data.
However, I have never found such a function useful for something related to notation.
Evidence
Someone asked for evidence.
The biggest problem is the submission of long evidence that was automatically found using a computer.
A large amount of work has been done to present evidence in Mathematica . An example is the Theorema project .
The most difficult proofs to represent, say, in logic, are some sequence of transformations. Here is an example of such proof:
Given are Schaeffer axioms for logic ( f is NAND ):
{f [f [a, a], f [a, a]] == a, f [a, f [b, f [b, b ]]] == f [a, a], f [f [a, f [b, c]], f [a, f [b, c]]] == f [f [f [b, b] , a], f [f [c, c], a]]}
Prove the commutativity, that is, thatf [a, b] == f [b, a] :
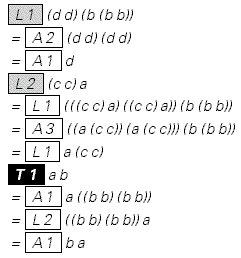
Remark (ab) is Nand [a, b] . In this proof, L == lemma , A == axiom , and T == theorem .
Character Selection
I would like to tell something about the choice of symbols for use in mathematical notation.
There are about 2,500 commonly used characters that are not found in plain text.
Some of them are too picturesque - say, a designation for fragile objects. Some are too ornate. Some are full of black fill, so they will stand out too much on the page (radiation symbol, for example).
But some may be quite acceptable.
If you look into history, you can often see a picture of how, over time, the spelling of some characters is simplified.
A particular problem that I recently encountered was the choice of a good designation for logical operations such as NAND, NOR, XOR.
In the literature on logic, NAND is designated differently:
I did not particularly like any of these designations. Basically they are filled with thin lines and are not integral enough to represent binary operators. However, they convey their content.
I came to the following notation for the NAND operator, which is based on the standard, but having an improved visual form. Here is the current version of what I came to:
Character Frequency Distribution
I mentioned the frequency distribution of Greek letters in MathWorld.
In addition to this, I also counted the number of different objects named with letters that appear in the dictionary of physical terms and mathematical abbreviations. Here are the results.
In earlier examples of mathematical notation, say, in the 17th century, ordinary words interspersed with various symbols.
However, more and more in areas such as mathematics and physics, there was a tendency to exclude words from the notation and name variables with one or two letters.
In some areas of engineering and social sciences, where mathematics has come not so long ago and is not too abstract, ordinary words can be found more often as variable names.
The same story with current trends in programming. And everything works well, as long as the formulas are simple enough. However, as the formulas become more complex, their visual balance is disturbed, and it becomes difficult to discern their general structure.
Parts of speech in mathematical notation
In the conversation about the correspondence between the language of mathematics and the ordinary language, I wanted to mention the question of parts of speech.
As far as I know, in all ordinary languages there are verbs and nouns, and in most of them there are adjectives, adverbs, etc.
In mathematical notation, you can represent variables as nouns and verbs as operators.
What about the other parts of speech?
Things like sometimes play the role of unions, as in ordinary languages (it is noteworthy that in all languages there are separate words for AND and OR, however, none of them have a word for NAND). And as a prefix operator, it can be considered as an adjective.
However, it is not completely clear to what extent the various types of linguistic structures associated with parts of speech in a common language are reflected in the mathematical notation.
For questions about Wolfram technologies, write to info-russia@wolfram.com