MIT course "Security of computer systems". Lecture 16: "Attacks through the side channel", part 3
- Transfer
- Tutorial
Massachusetts Institute of Technology. Lecture course # 6.858. "Security of computer systems." Nikolai Zeldovich, James Mykens. year 2014
Computer Systems Security is a course on the development and implementation of secure computer systems. Lectures cover threat models, attacks that compromise security, and security methods based on the latest scientific work. Topics include operating system (OS) security, capabilities, information flow control, language security, network protocols, hardware protection and security in web applications.
Lecture 1: “Introduction: threat models” Part 1 / Part 2 / Part 3
Lecture 2: “Control of hacker attacks” Part 1 / Part 2 / Part 3
Lecture 3: “Buffer overflow: exploits and protection” Part 1 /Part 2 / Part 3
Lecture 4: “Privilege Separation” Part 1 / Part 2 / Part 3
Lecture 5: “Where Security System Errors Come From” Part 1 / Part 2
Lecture 6: “Capabilities” Part 1 / Part 2 / Part 3
Lecture 7: “Native Client Sandbox” Part 1 / Part 2 / Part 3
Lecture 8: “Network Security Model” Part 1 / Part 2 / Part 3
Lecture 9: “Web Application Security” Part 1 / Part 2/ Part 3
Lecture 10: “Symbolic execution” Part 1 / Part 2 / Part 3
Lecture 11: “Ur / Web programming language” Part 1 / Part 2 / Part 3
Lecture 12: “Network security” Part 1 / Part 2 / Part 3
Lecture 13: “Network Protocols” Part 1 / Part 2 / Part 3
Lecture 14: “SSL and HTTPS” Part 1 / Part 2 / Part 3
Lecture 15: “Medical Software” Part 1 / Part 2/ Part 3
Lecture 16: "Attacks through the side channel" Part 1 / Part 2 / Part 3
Audience: Do you use the Karatsuba method?
Professor: Yes, this is a clever multiplication method that does not require four stages of computation. Is the Karatsuba method taught in the .601 course, or how is it designated today?
Audience: 042.
Prof: 042, excellent. Yes, this is a very good method. It is used by almost every cryptographic library. For those of you who are not graduates of our institute — I say this because we have graduate students here — I will write about the Karatsuba method on the blackboard. Here you need to calculate three values:
a 1 b 1
(a 1 - a 0 ) (b 1 - b 0 )
a 0b 0
So you do 3 multiplications instead of four, and it turns out that you can recover this value a 1 b 0 + a 0 b 1 of these three multiplication results.
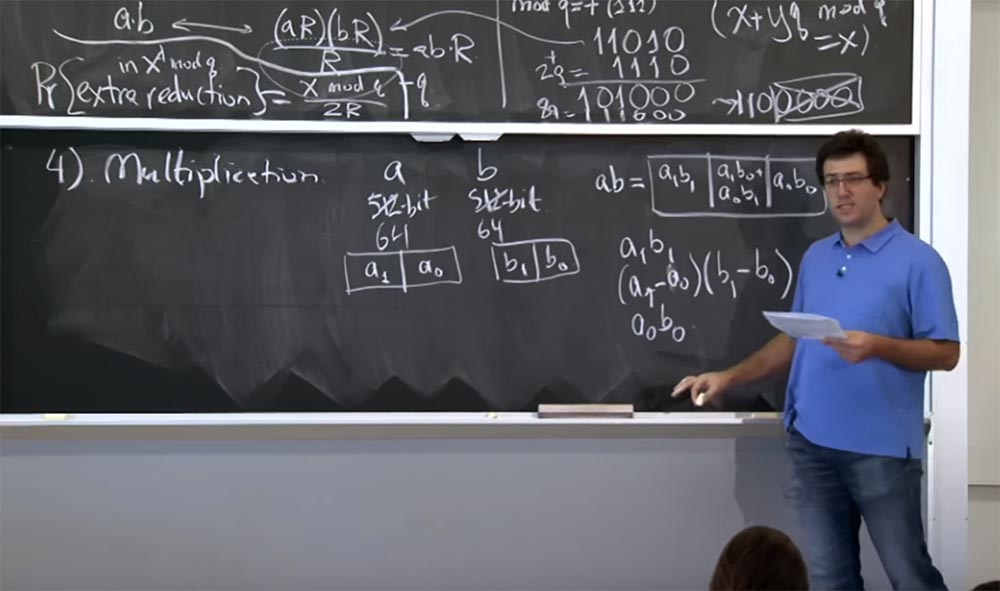
The special way to do this is this ... let me write it in a different form.
So, we will have:
(2 64 + 2 32 ) (a 1 b 1 ) +
(2 32 ) (- (a 1 - a 0 ) (b 1 - b 0 )
(2 32 + 1) (a 0 b 0)
This is not very clear, but if you work through the details, then ultimately convince yourself that this value in these 3 lines is equivalent to the value of ab, but at the same time reduces the computation by one multiplication. And the way we apply this to more voluminous multiplications is that you continue to go down recursively. So, if you have 512 bit values, you can break them into 256-bit multiplication. You do three 256-bit multiplications, recursively using Karatsuba's method each time. In the end, your calculations are reduced to engine size and can be processed by a single machine instruction.
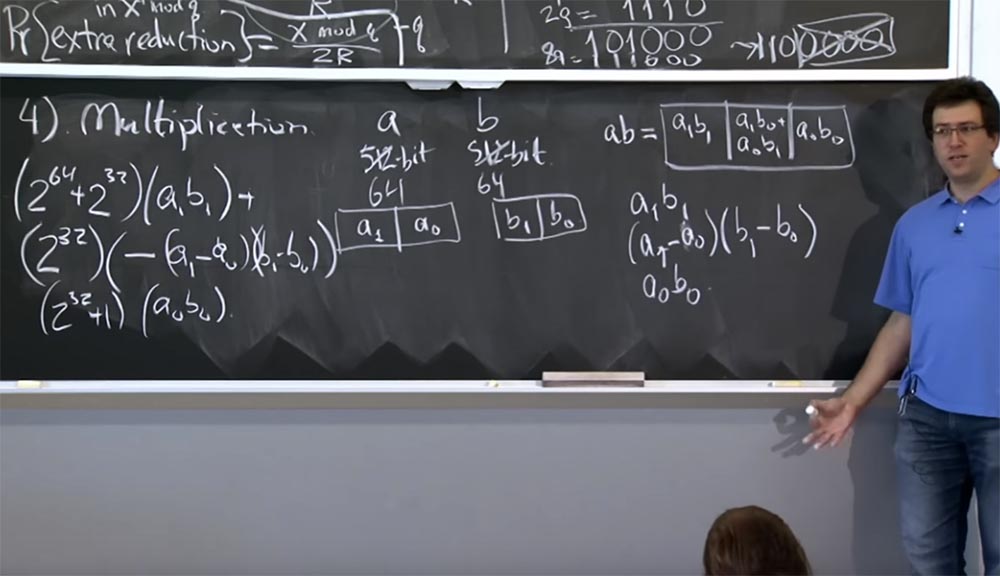
So where is the timings attack here? How do these guys use Karatsuba multiplication? It turns out that OpenSSL is worried about two types of multiplication that you may have to do.
The first is the multiplication of two large numbers of approximately the same size. This happens many times when we perform modular exponentiation, because all the values that we multiply will be approximately 512 bits in size. So when we multiply c by y or square it, we multiply two things about the same size. In this case, the Karatsuba method makes a lot of sense, because it reduces the size of the numbers squared by about 1.58 times, which speeds up the process of calculations a lot.
The second type of multiplication is when OpenSSL multiplies two numbers, the size of which differs significantly from each other: one is very large and the other is very small. In this case, you could also use the Karatsuba method, but it will run slower than primitive multiplication. Suppose you multiply a number of 512 bits by a 64-bit number, you will have to raise each bit of the first number to 64 degrees, and as a result you get a 2n process slowdown instead of acceleration n / 1.58. Therefore, these guys using OpenSSL, tried to get smarter, and this is where the problems started.
They decided that they would dynamically switch between the effective Karatsuba method and the primary school multiplication method. Their heuristics were as follows. If the two numbers that you multiply consist of the same number of machine words, or at least have the same number of bits as 32-bit units, then the Karatsuba method is used. If two numbers are very different in size from each other, squaring or direct simple, normal multiplication is performed.
At the same time, you can track how the switch to another multiplication method. Since the moment of switching does not pass without a trace, it will be noticeable after it, whether it takes much more time to multiply now or much less than before. This circumstance was used by researchers to organize an attack using the method of determining timings.
I think that I’ve finished telling you about all the strange tricks that people use to put RSA into practice. Now let's try to put them together and use against the whole web server to find out how you can “pinch” the bits of interest to us from the input network packet.
If you remember from the HTTPS lecture, the web server has a secret key. He uses this secret key to prove that he is the correct owner of all certificates via HTTPS or TLS. This is due to the fact that clients send some randomly selected bits, these bits are encrypted using the server's public key, and the server decrypts the message using the TLS protocol. And if the message is verified, then these random bits are used to establish a communication session.
But in our case, this message will not be checked, because it will be created in a special way, and when it turns out that the additional bits do not match, the server will return an error as soon as it finishes decrypting our message.
That's what we're going to do here. The server - you can assume that it is Apache with SSL open - will receive a message from the client, which will count the encrypted text with or some hypothetical encrypted text that the client has created. The first thing we do with ciphertext is decrypt it using the formula c → (c d mod n) = m.
If you remember the first optimization, we are going to apply the Chinese remainder theorem and divide our text into two parts: one to calculate mod p, the other mod q, and then combine the results. First we take c and present it in two quantities: the first one will be called c 0 , it will be equal to mod q, and the second one we will denote c 1, and it will be equal to c mod p. Then we do the same to calculate c for d mod p and c for d mod q.

Next we are going to switch to the Montgomery representation, because it will make our multiplications very fast. So the next thing SSL is going to do with your number is to calculate c 0 ', which will be equal to c 0 R mod q and do the same here, for c1, I will not record it because it looks the same .
Now that we are in the form of Montgomery, we can finally produce our multiplications, and here we will use the “sliding window” technique. As soon as we get c 0 ', we will complete this simple construction of c 0'to the power d modulo q. And here, since we calculate this value for d, we will use “sliding windows” for the exponent bits d, and also apply the Karatsuba method or the usual multiplication depending on what the size of our operands is.
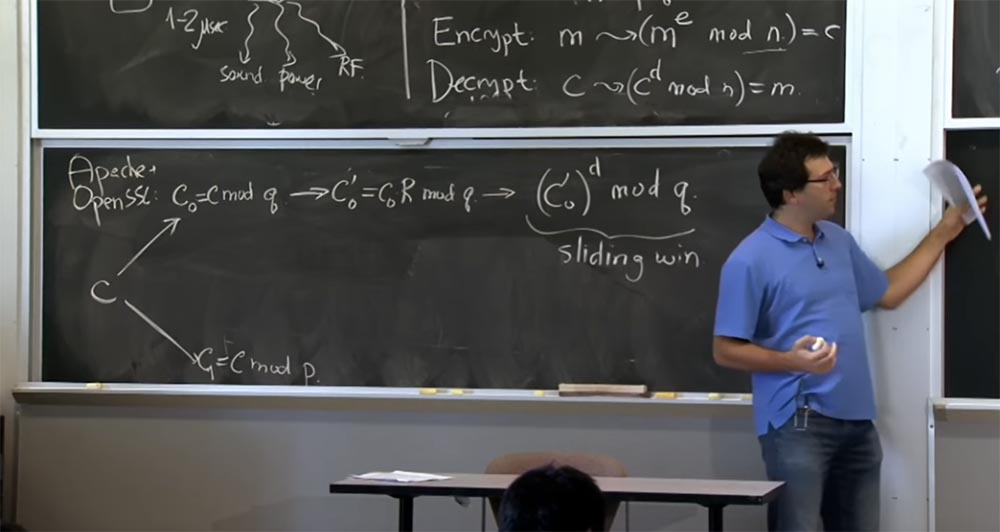
So, if it turns out that this value is c 0 'and the previously obtained squaring result is the same size, we use the Karatsuba method. If c 0 'is very small and the previous result of multiplication is large, then we will square it and multiply it in the usual way. Here we use "sliding windows" and the Karatsuba method instead of normal multiplication.
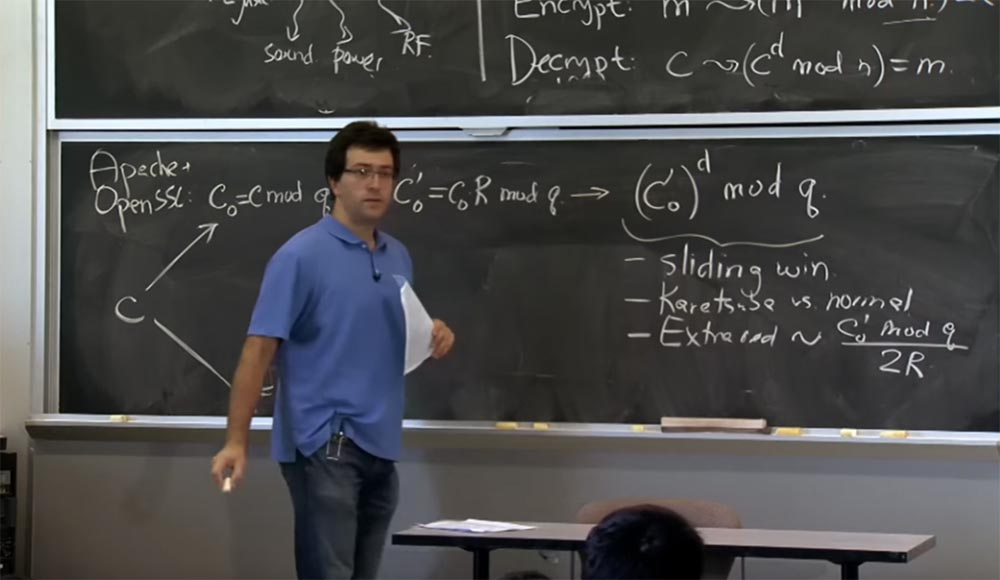
Also at this stage additional reductions appear. Because with each multiplication, the additional abbreviations will be proportional to what we are raising to the power modulo q, that is, to the value (c 0 ') d . Here, with a simple connection of the formula, the probability of additional reductions will be proportional to the value of c 0 'mod q divided by 2R. It is in this place that a bit appears that affects timing.
In fact, there are two possible effects here: using the Karatsuba method instead of normal multiplication and the appearance of additional cuts that you are going to make.
In a second you will see how it can be used. Now, when you got this result for mod q and are going to get a similar result for mod p, you can finally recombine these two parts above and below and use CRT, the Chinese theorem on residuals.
And what you end up with from CRT ... sorry, I think we first need to convert it back from the Montgomery form. Therefore, before recombination, we transform the upper part into the expression (c 0 ') d / R mod q and return our value cd mod q. In the lower part, we respectively obtain cd mod p.
You can now use CRT to get the value of c dmod n. Sorry for the small font, I did not have enough boards. Approximately the same thing we have here below for with 1 , and we can finally get our result, that is, the message m.

Thus, the server takes an incoming packet that receives it, runs it through the entire pipeline, runs the two parts of this pipeline, and ends with the decrypted message m, equal to cd mod m. Then he is going to check the padding padding of this message. In the case of our specific attack, we created with in such a way that in fact this addition will not coincide. We chose the value of c for such heuristics that do not encrypt the real message with the correct padding padding.
Thus, the addition will not withstand the test, the server will need to write an error, send an error message to the client and terminate the connection. So, we are going to measure the time it takes the server to pass our message through this pipeline. Have questions about the message processing process of the server and the integration of all these optimizations?
Audience: in my opinion, there is an error with the index of the value of c.
Professor: yes, you are right, I finish the index 0, here it should be c 0 d mod q.
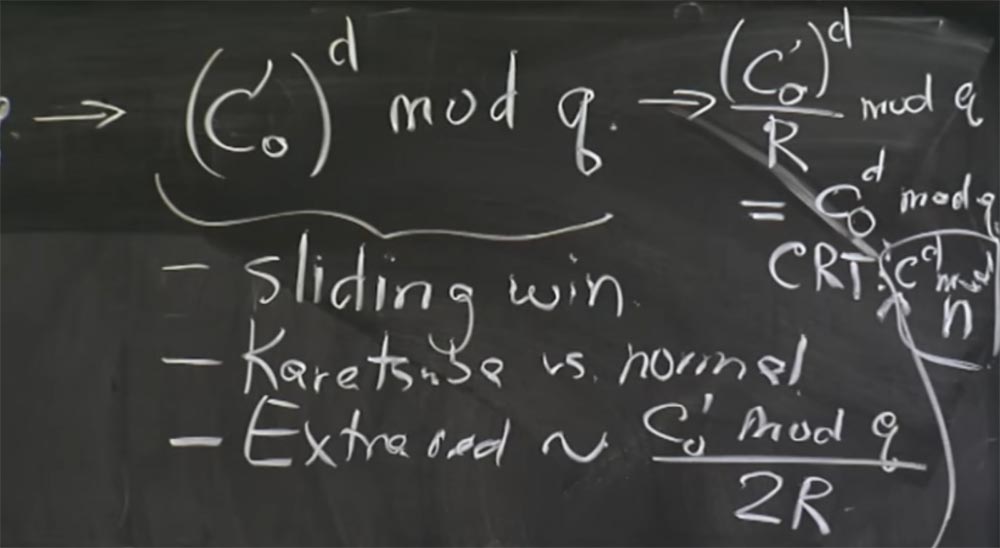
Audience: when you divide by R mod q, aren't there any assumptions about how much q you should add to further reduce low bits by zeros?
Professor:Yes, you are right, at this final stage (c 0 ') d / R mod q there may be additional abbreviations. So we have to do this division of R in the right way, and probably have to do the same thing as when doing the Montgomery cut here when we divide by R to convert the value back. Since at the beginning of the calculations it is not clear how much q we should add, we use the selection method, destroy low zeros, then do mod q again, and possibly an additional abbreviation. You say absolutely true, in this case it is exactly the same division by R mod q, as for each step of the Montgomery multiplication.
So how to use it? How can an attacker unravel the server's secret key by measuring the time of operations? These guys have a plan that is based on guessing one bit of the private key at a time. We can assume that the secret key is an encrypted exponent d, because you know e and you know n, it is a public key. The only thing you do not know is d.
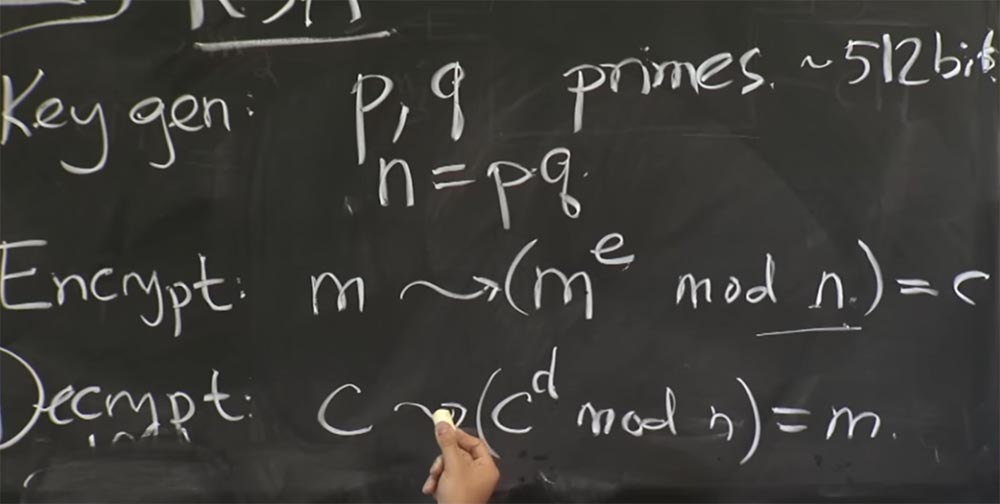
In fact, in this attack they do not directly guess the value of d, since it is rather difficult. Instead, they consider the value of q or p, no matter which of these two quantities. As soon as you guess what value is p or q, you can calculate n = pq. Then, if you know the values of p and q, you can calculate the function φ, which we talked about earlier. This will allow you to get the value of d from the value of e. Therefore, this factorization of the n value is extremely important; it must be kept secret to ensure RSA security.
So actually, these guys intended to guess the value of q by analyzing the timings of this pipeline. What are they doing for this? They carefully select the initial value of c and measure the time it passes through the server pipeline.
In particular, there are two parts to this attack, and you must take some initial steps to guess the first few bits. Then, as soon as you have the first few bits, you can guess the next bit. So let me not tell in detail how they guess the first couple of bits, because it's actually much more interesting to see how they guess the next bit. If we have time, we will return to how the guessing of several initial bits in a lecture article is described.
So let's say that you have an assumption g about which bits are in the meaning of this q. Let this quantity consist of such bits: g = g 0 g 1 g 2… and so on. Rather, it is not even g, but the real bits of q, so let me rewrite it in this form: g = q 0 q 1 q 2 .... We believe that these q are high bits, and we are trying to guess the bits lower and lower. Suppose we know the value of q up to the bit qj, and then all the zeros follow. You do not guess what the other bits are.
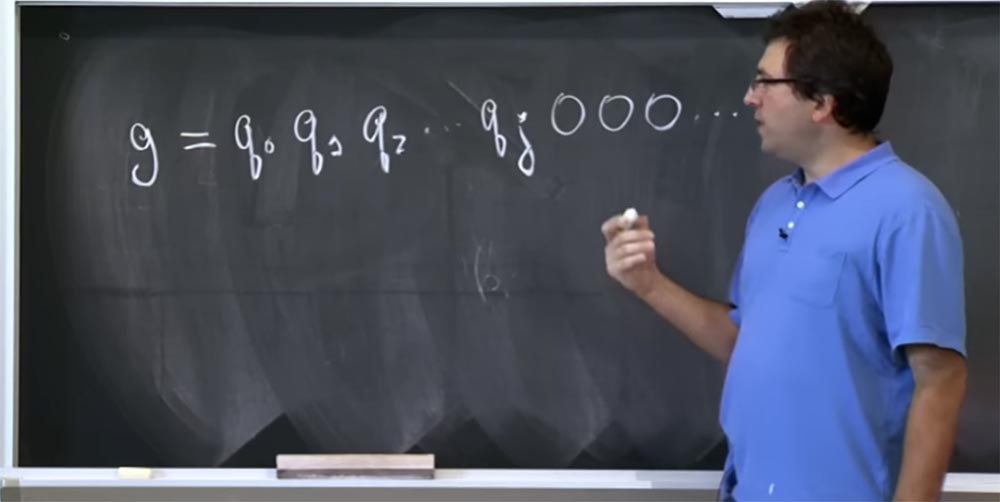
These guys tried to inject this guess g into this place of our pipeline: (c0 ') d mod q. Because this is the place where two types of optimization are used: the Karatsuba method instead of the usual multiplication and a different number of additional reductions depending on the value of c 0'. Actually, they tried to inject two different guesses into this place of the conveyor: the first, which looks like g = q 0 q 1 q 2 ... qj 000 ... 0000 and the second, which they called g high , which consists of the same high bits, but instead at the end of all zeros there is a unit that means a high bit, followed by zeros again:
g = q 0 q 1 q 2 ... qj 100 ... 0000.
How does this help these guys understand what's going on? There are two ways to do this. Suppose that our guess g is equal to the value of c 0 '. We can assume that these g and g high correspond to the value c 0', shown on the left board. In fact, it is quite simple to do this, because c 0 'is quite easily calculated the opposite way from the encrypted input value c 0 , you simply multiply it by R.
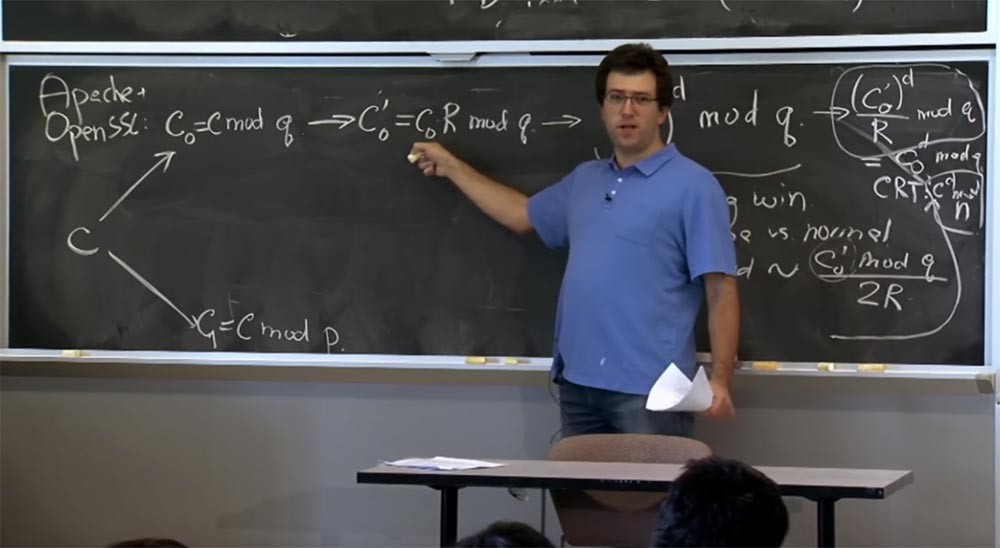
Therefore, to guess the value (c 0 ') d , they just need to take their guess, his guess g and first divide it into R, that is, divide into 512 mod something there. Then they are going to enter it back, the server will multiply it by R and continue the process given in our pipeline scheme.
So, suppose we managed to put our particular selected integer value in the right place. So, what is the computation time from c 0 'to d mod q?

There are two possible options where q fits into this picture. It may be that q is between these two values of g and g high , because the next bit q is 0. Thus, this value — the first 0 after qj — will be less than q, but this value — 1 after q — will be greater than q. This happens if the next bit q is 0, or it is possible that q is above both of these values, if the next bit q is 1.
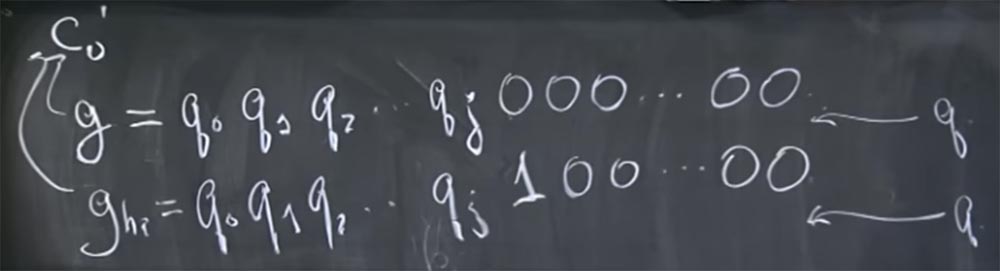
Now we can tell what the decryption time of these two values will be if q is between them, or q is located above both of them.
Let's consider the situation where q is located above. In that case, everything is pretty much the same. Since both these values are less than q, then the value of these things mod q will be about the same. They are somewhat different due to this extra bit, but still more or less the same size. And the number of extra reductions will probably also not be very different, because it is proportional to the value of c0 'mod q. And for both the g and g high valuessmaller q, they are about the same. Neither of them will exceed q and will not cause a large number of additional reductions, because when q is greater than both of these guesses, the number of calculations by the Karatsuba method relative to the number of ordinary calculations will remain the same. In terms of this relationship, the server will handle both g and g high in the same way . Therefore, the server is going to make about the same additional reductions for both of these values. Thus, if you see that the server spends the same time to answer these guesses, then you should probably assume that, in the value of g high, there is indeed 1 in this place.

On the other hand, if q is located between these two values, then there are two possible things that can cause switching and changing timings. One of the things is that since g high is slightly larger than q, the number of additional cuts will be proportional to c 0 'mod q, which is very small, because c 0 ' is q plus some bits in this additional sequence of 100 bits ... 00 Thus, the number of additional reductions will be more noticeable and everything will start to happen faster.
Another possible thing that can happen is that the server may decide: “oh, now it’s time to do normal multiplication instead of Karatsuba’s method!”. Maybe for this value of g the value of c 0'will have the same number of bits as q, and if it turns out that g high is greater than q, then g high mod q will potentially have less bits. And if it crosses a certain border, the server will suddenly switch to regular multiplication. In this case, we will observe the reverse process - everything will start to flow more slowly, because the usual multiplication takes more time than the multiplication of Karatsuba.
The number of additional cuts is proportional to c 0 'mod q. If c 0 which is this value g high, a little more than q, this is a tiny difference, which will not be comparable to the difference between g and q. In this case, there will also be a change in timings, which you can try to measure. So actually, there are a few interesting things here, when these effects actually work in different directions. So, if you set a 32-bit switching boundary between Karatsuba’s method and normal multiplication, then decoding this message will take much longer.
On the other hand, if the 32-bit border is not applied here, it is possible that the effect of additional cuts will tell you what is happening here. Thus, in fact, you should monitor the various effects. If you do not guess a few bits within 32 bits, then you should expect that the time will decrease due to additional cuts. On the other hand, if you are trying to guess a bit that is a multiple of 32, then perhaps you should expect a Karatsuba effect, or multiplication will be done in the usual way.
Therefore, if you look at what is written in a lecture article, then these guys did not pay attention to jumping timings up or down. You just have to expect that if the next bit q is 1, then these things take almost the same amount of time, and if the next bit q is 0, then you should expect these values to be ghigh and q have a noticeable difference, even if it is more or less, positive or negative.
So in fact, the authors of the article measure just that. It turns out that this method works very well. But in fact, they have to do two interesting tricks to make it all happen. If you remember, the time difference was tiny, on the order of 1-2 microseconds. Such a difference is very difficult to measure through a regular network, for example, through an Ethernet switch.
Therefore, they make two types of measurements, two types of averaging. They send each guess several times. The article says that they sent these values to the server 7 times or so. So, what kind of interference do you think it helps them to simply repeat the same assumption, the same guess again and again?
Lecture hall:How about using different links?
Professor: yes, so if the network allows you to use different links, you can try to send the same thing many times, and its processing on the server should take the same amount of time each time, so you can average the network noise, or network interference . The article says that they take the average network noise.
But then they do another strange thing, which is that they do not just send the same guess 7 times, they actually send a whole family of guesses, where each is slightly different from the previous one and each new value is sent 7 times. That is, first they send g 7 times, then they send g + 1 7 times, then g + 2 also 7 times and so on up to g + 400. Why do they average different values of g rather than just send g, say, 7 400 times, is it so much easier?
Audience: probably to better estimate the time that a server spends?
Professor: yes, this is actually the case, we are trying to measure how much time this part of the calculations will take - (c 0 ') d. But there are many other things. For example, the other pipeline, which is at the bottom, performs all calculations mod p. I mean that it will also take a different amount of time depending on what the input values are. The useful thing is that if you change the value of all your guesses g, adding 1, 2, 3, whatever, it adds a little bit of bits.
If we now look at the attack by the timing method, we have little change, because everything depends on turning over this middle bit - units in the sequence 100 ... 00. But everything that happens in the lower part of the pipeline with mod p will be completely randomized by this, because when calculating mod-p, adding an extra bit can change the whole process. Then you are going to average out other kinds of “computational noise,” which is deterministic for a particular value, but not related to this part of the calculation (c 0 ') d that we are trying to perform. It's clear?
Audience: what do they do when they try to guess the lower bits?
Professor:in fact, they use some other mathematical trick to guess only the upper half of the q bits. It turns out that if you know the upper half of the q bits, there is some kind of math that allows you to determine the factor of numbers, and you are the winner.
Audience: how do you get the value c 0 '?
Professor: if you need the value c 0 ', you have to create the value c, simply by taking the prime number c 0 ' and multiplying by the inverse of the value of R modulo n.

And when the server takes this value, it “pushes” it here to calculate this expression c 0 = c mod q, so that it will look like c 0 = ((c 0 'R -1) mod n) mod q. Then you multiply it by R to get rid of the inverse R. And then you ultimately determine exactly the value c 0 ', which is located in the expression (c 0 ') d mod q. So the cool thing is that all the manipulations performed here simply boil down to multiplying R by that. And you know that R = 2,512 . I think everything will be simple here.
Audience: Can we, when determining timings, abandon calculations using mod p at the bottom of the pipeline?
Professor:that is, you do not know what p is, but you want to define it at random? If you succeed, you will do a great job! Well, next week we will begin to discuss other issues.
Full version of the course is available here .
Thank you for staying with us. Do you like our articles? Want to see more interesting materials? Support us by placing an order or recommending to friends, 30% discount for Habr's users on a unique analogue of the entry-level servers that we invented for you: The whole truth about VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps from $ 20 or how to share the server? (Options are available with RAID1 and RAID10, up to 24 cores and up to 40GB DDR4).
VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps until December for free if you pay for a period of six months, you can order here .
Dell R730xd 2 times cheaper? Only here2 x Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 TV from $ 249 in the Netherlands and the USA! Read about How to build an infrastructure building. class c using servers Dell R730xd E5-2650 v4 worth 9000 euros for a penny?
