Proof of availability of places where symmetries cannot exist.
- Transfer
A major mathematical achievement was the proof of the Zimmer hypothesis, found by a small team of researchers

In lattices in higher dimensions of symmetry, it is not always possible to transfer to measurements below the rank.
The success of Robert Zimmer can be defined in different ways. As president of the University of Chicago since 2006, he hit the headlines, finding nine-digit amounts for funding and publishing articles in support of free speech on campus. But before becoming a university president, he was a mathematician. And after a long time after he left serious research, the research plan launched by him finally gives his results.
A year ago, three mathematicians proved the Zimmer hypothesis related to the circumstances in which geometric spaces have symmetries of a certain type. Their proof has become one of the greatest mathematical advances in recent years. It puts an end to the question that stood before Zimmer during his intense mental activity in the late 1970s and early 1980s.
“I would say that for five years I went to bed with thoughts about this task every night, so I was obsessed with it, and it’s great to watch how people solved it,” said Zimmer.
Usually, the larger the geometric dimension space, the more symmetries can be in it. This can be represented by studying a circle that exists on a two-dimensional plane, and a ball that extends in three dimensions: there are more ways to rotate a ball than methods to rotate a circle. Additional ball measurements create additional symmetries.
Zimmer's hypothesis refers to the symmetries of a special kind, known as high-ranking grids. She asks whether the measurement of geometric space limits the use of symmetries of this type. The authors of the new work are Aaron Brown and Sebastian Hurtado-Salazar of the University of Chicago and David Fisher.from Indiana University –– they showed that when the number of measurements is less than a certain, specific symmetries are not observed. Thus, they proved the correctness of Zimmer’s hypothesis.

Robert Zimmer, now president of the University of Chicago, developed a hypothesis, named after him, almost 40 years ago.
Their work answers one important and long-standing question, revealing new ways of exploring many others. It also reveals the intrinsic properties of geometric spaces. Symmetry is one of the simplest properties of such spaces. The new paper says that symmetries can exist in spaces of one type, and cannot - in others. This achievement was achieved after decades of downtime.
“The hypothesis looked like it could take people for a very long time,” said Aimee Wilkinson, a mathematician at the University of Chicago, who organized a conference this year on this evidence. "And they relatively simply destroyed the matter."
Satisfying symmetries
Symmetry is one of the first geometrical concepts that children encounter in mathematics. With their own hands, they will learn that they can rotate, turn over and shift the form, and eventually get the same form with which they started. Preserving the shape of an object as a result of changes responds with a certain inner satisfaction - this is a hint of the presence of a deeper order in the Universe.
Mathematicians have their own formal language for studying symmetry. It gives them the opportunity to talk in various terms about various symmetries that are applicable in a given geometric space.
A square, for example, has eight symmetries — eight ways to flip or turn it, again getting a square. The circle can be rotated by any number of degrees; She has an infinite number of symmetries. Mathematicians collect all the symmetries of a given geometric object, or space, and pack them into a "group".
Groups are interesting in their own right. They often appear as a result of studying certain geometric spaces, but sometimes they also appear in a completely unconnected context with geometry. For example, groups can form numerical sets (for example, there is a certain symmetry in adding 5 or subtracting 5 from a number).
“A group, in principle, can appear as a symmetry of completely different things,” said Zimmer.
There are more exotic types of symmetry than those that we learn in school. Consider, for example, lattice symmetry. The simplest grid is a two-dimensional grid. On the plane, the grid can be moved up, down, left, right to any number of squares, and you can get a grid that looks exactly like the original. You can also reflect the grid through any number of individual cells. Spaces with lattices possess an infinite number of different symmetries of lattices.
Grilles can exist in any number of dimensions. In three-dimensional space, the lattice may consist of cubes, and not of squares. In four or more dimensions, the grid cannot be imagined anymore, but it works in the same way; mathematicians can describe it exactly. Groups of interest to the Zimmer hypothesis include “higher rank” lattices, or lattices in certain higher dimensional spaces. “This strange lattice would be very beautiful if it could be seen, even if it is not given to me,” said Hurtado-Salazar. “It seems to me that looking at her would be very nice.”
In the 20th century, mathematicians discovered these groups in various conditions — not only in geometry, but also in number theory, logic, and computer science. Opening new groups, it is logical to ask the question - what kind of spaces have such sets of symmetries?
Sometimes groups are obviously impossible to match with space. One can quickly understand that the symmetry group of a circle cannot be applied to a square. Turn the square by 10 degrees and you will not get the original square. But a mixture of a group with an infinite number of symmetries and a space with many dimensions makes it difficult to determine the applicability of a group.
“As we move to a more complex group in more dimensions,” said Zimmer, “these issues become very complicated.”
Indirect link
Imagine symmetry, we represent the rotation of the whole form - for example, a square rotated 90 degrees. But at the basic level, symmetry depends on moving points. Symmetric transformation of space means that you need to take each of its points and move it to some other point. In this sense, turning a square by 90 degrees actually means taking every point of a square, and turning it 90 degrees so that it is not on the edge from which it started.

David fisher
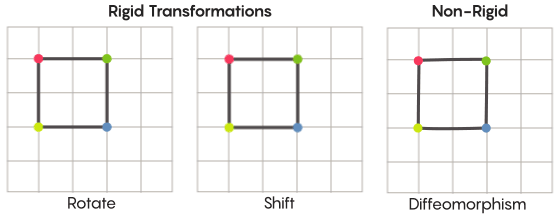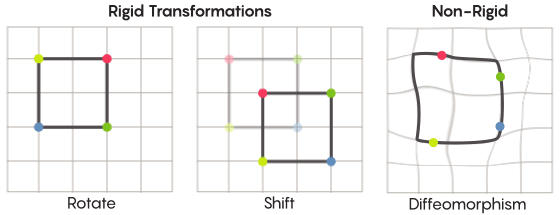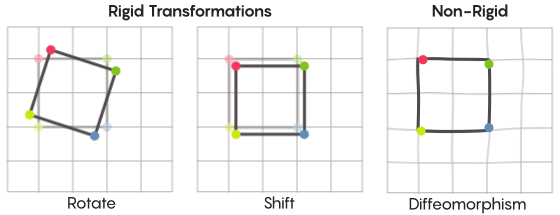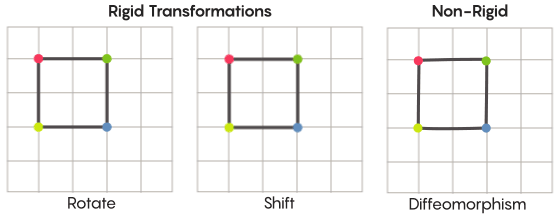
The task of moving points can be solved more or less strictly. The symmetrical transformations most familiar to us — the reflection of a square relative to a diagonal or its rotation by 90 degrees — are very strict. Strict in the sense that they do not confuse points. The points that were vertices before the reflection remain vertices after (they just become different vertices), and the points that make up the direct edges after the reflection still make up the straight edges (just different ones).
There are less strict, more flexible types of symmetric transformations, and they are interesting in the context of the Zimmer hypothesis. In such transformations, points change their organization more strongly; they do not necessarily retain their previous connections with each other after transformation. For example, you can shift each point of a square by three units of length along the perimeter of a square — this satisfies the basic requirements of a symmetric transformation, that is, simply shifting each point in space to another place. Aaron Brown, the co-author of the proof, described how these, freer types of transformations might look in the context of the ball.
“You can take the north and south poles and twist them in opposite directions. Then the distances between the points will increase, ”said Brown.
In the case of a grid, instead of simply shifting it along a plane, you can bend it, stretch it in some places and compress it in others, so that the transformed mesh no longer overlaps the original one. Such transformations are less strict, and are called diffeomorphisms .
Zimmer had good reasons to use this less stringent version of symmetry in his hypothesis. Special grids of higher rank related to this hypothesis were first studied in the 1960s by Grigory Alexandrovich Margulis , who received the Filds Award for his work . Margulis has compiled a complete description of what kind of spaces can be transformed with the help of these higher-order grids, if only strict transformations are allowed.
Zimmer’s hypothesis was a natural continuation of Margulis’s work. It begins with a list of spaces on which higher-level grids can work — this list was discovered by Margulis — and asks if this list expands, if lattices are allowed to have less stringent transformations.
In the new work, three mathematicians proved that weakening the definition of symmetry does not change the scope of application of symmetries of higher-order lattices. Even if gratings are allowed to be very irregular transformations - to shift, bend, stretch - the grids still have a hard limit to the scope.
“After adding such flexibility to the task condition, intuitively, of course, it seems that the grids will be able to act more widely. Therefore, it turns out surprising that in reality the answer will be “no” - in some cases they cannot, ”said Fisher.
Mathematicians have established exact correspondences between the dimension of space and the dimension, or rank, of lattices, for lattices capable of playing the role of symmetry in a given space. In general, they showed that the higher the rank of the lattice, the more dimensions needed for the space that can accommodate it. Even with considerable flexibility in the transformation of space, the transformation of high-ranking grids is limited to higher dimensions.
“This suggests that there is something very fundamental in the structure of spaces, from which follows their ability to accommodate such transformations,” said Wilkinson.
Zimmer's hypothesis is just the first step to a larger program. Having dealt with it, the collaborators of the work imposed a gross restriction on the spaces in which high-ranking grids can be transformed. The next, more ambitious phase of work will be the concentration on those spaces in which lattices can exist - and then the classification of all the different ways of transformation by the lattices of these spaces.
“As a result, the program should be able to classify all these methods. There are many interesting issues outside of simply establishing the existence of certain places in which the grids cannot operate, ”said Zimmer.
