More on the development of X-ray tomography software

Scientists from Tomsk State University have created a microtomograph. A tomograph allows you to learn the exact structure of various materials, such as diamonds, with micron accuracy.

But it’s more interesting to stuff a fly into it.



Before EDISON Software Developement tasked to write software for microtomograph. About how they successfully coped with the task, there was an article chookcha on Habré ( How to create software for a microtomograph in 5233 man-hours ) with a description of algorithms, mathematical methods, implementation and debugging.

Insatiable readers bombarded us with questions to which we finally formulated the answers ...

A tomograph can enlighten material with a resolution of up to microns. It is 100 times thinner than a human hair. After scanning, the program creates a 3D model where you can look not only at the outside of the part, but also find out what is inside it.

Question number 1

I would love to read about the inverse of the Radon transform with a point source and about the implementation of all this using the CUDA Uranix

Radon calculation for a point source, if described schematically, is similar to the calculation for parallel mode, but only the direction of the rays is not parallel, which affects the coordinates of the points in the cube an object where densities are added. With such a schematic description, from the point of view of reconstruction, there is no big difference which algorithm to use, only the coordinates of the segments / rays and the formula for calculating them change.

Further, when on the basis of the shadow projection we received rays from the source to each projection point in the coordinate space of the microtomograph, knowing the position of the rotating cube of the object, voxels lying on the beam are calculated along each of the rays. Each voxel is assigned a pixel density of the shadow projection, which includes the ray from the source, the data type of the weights is converted to float. As a result, for each shadow projection, we repeat this projection projection onto the voxels, taking into account the projection angle. After that, all the total values ​​of voxels are normalized to the capacity in which they will be stored in the future, usually it was a 16-bit integer unsigned. This description maximally simplifies the scheme of reconstruction and obtaining the final voxel model, the following is a more detailed description of this algorithm.

The X-ray system generates a flat shadow image of the full internal volumetric structure of the sample, but in a separate shadow projection of the deep distribution of the sample structures are completely mixed. Only x-ray tomography allows you to visualize and measure the spatial structures of the samples without their chemical and mechanical processing.


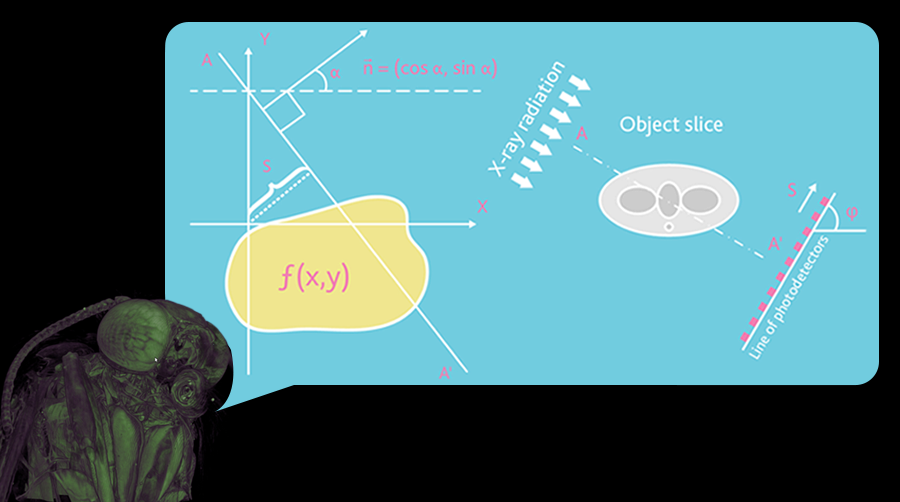
Fig. 1. The geometry of parallel beams

Any x-ray shadow image is a flat projection of a three-dimensional object. In the simplest case, we can describe it as an image obtained in parallel x-rays (Fig. 1). In this approximation, each point of the shadow image contains summary information on the adsorption of a particular x-ray beam over the entire volume of a three-dimensional object. For the parallel geometry of X-ray beams, the reconstruction of a three-dimensional image of a sample from a two-dimensional shadow projection is realized using reconstructions of a series of two-dimensional sections of the sample along one-dimensional shadow lines. The possibility of such reconstructions is demonstrated by a simple example: consider an object with a single point with high adsorption in an unknown place.


Fig 1.1. Schematic representation of three different positions of the absorbing region and the corresponding reconstruction from the obtained shadow projections

In a one-dimensional shadow line, a decrease in intensity will be observed due to its absorption on an absorbent object (Fig. 2). Now we can simulate in computer memory an empty row of pixels (image elements) corresponding to the estimated displacement of the object. Naturally, you should make sure that all parts of the reconstructed object will be in sight. Since we have the coordinates of the shadows from the absorbing areas of the object, we can select in the reconstructed area in the computer memory all the possible positions of the absorbing areas inside the object in the form of lines. Now we begin to rotate our object and repeat this operation. In each new position of the object, we will add to the reconstructed area lines of the possible positions of the object in accordance with the position of its shadow projections. This operation is called back projection. After several revolutions, we can localize the position of the absorbing region within the reconstruction volume. With an increase in the number of shadow projections from various directions, this localization becomes more and more clear (Fig. 3).


Fig. 2. Reconstruction of a point object using a different number of offsets

In the case of reconstruction based on an infinite number of projections, an image is obtained with good clarity of determining the position of the absorption region inside the object under study. At the same time, the point image will be accompanied by a blurred area, since it was obtained in the course of overlapping lines with all possible deviations. Now, since we know that the image is formed by a point object, we can carry out a preliminary correction of the initial information in the sorption lines to make the final image more relevant to the real object. This correction adds a certain amount of negative adsorption along the outer border of the point to remove the blur inherent in the back projection process (Fig. 4). This algorithm gives not only images of sections of individual point structures, but also allows you to explore real objects. Each material object can be represented as a large number of individual elementary absorbing volumes and linear adsorption in each x-ray beam corresponds to the total adsorption on all absorbing structures encountered by the beam.


Fig. 3. Filtering the rear projection

Thus, two-dimensional sections of the object can be restored from one-dimensional shadow lines from different angles. However, most x-ray emitters are not able to generate parallel beams of radiation. In reality, point sources producing conical x-ray beams are used.


Fig. 4. The geometry of the diverging beam

In fan geometry, the reconstructed sections will have some distortions in areas remote from the optical axis of the beam. To solve this problem, we must use the three-dimensional conical beam reconstruction algorithm (Feldkamp) to take into account the thickness of the object. In other words, the rays passing through the front and back surfaces of the object will not be projected onto the same row of the detector (Fig. 6). Thus, the most rapidly reconstructed section is the axial section, since it does not require correction for the thickness of the sample.


Fig. 5. Conical beam geometry

In the case of a fluoroscopy of a sample, the image contains information about a decrease in the intensity of the incident radiation inside the object. Since X-ray absorption is described by an exponential dependence (Lambert-Beer law), linear information about the adsorption of radiation from a shadow image can be disclosed using a logarithmic function. Since the logarithm is a nonlinear operation, the slightest noise in the signal leads to significant errors in reconstructions. To get rid of such errors, averaging of the initial data can be used. On the other hand, we could try to improve the signal-to-noise ratio in the shadow image by optimizing the exposure time to accumulate the most representative information. The most effective way of noise reduction in the reconstruction process is the correct choice of the correction / filtering function for convolution before reverse projection. In the simplest case (described above), the correction function produces two negative adsorption reactions around any peak of the signal or noise in the shadow line, and this behavior becomes very dangerous when working with a noise signal. The choice of the convolution function with spectral constraints (the Hamming window) for corrections allows us to solve this problem.

CUDA Job Description and Reconstruction

Shadow projection reconstruction

The maximum cube size for reconstruction is 1024x1024x1024 voxel. We call such a cube unit. The algorithm allows you to reconstruct smaller cubes, but the dimension in all directions should be a multiple of 32. For one approach, a layer of a cube is reconstructed, with a volume of not more than 128 MB, i.e. 1/8 unit cube. If several CUDA devices are installed in the system, then reconstruction on them will go in parallel.

Loading in RAM of shadow projections is made at the first pass, in an amount sufficient for reconstruction of the cube. Those. if reconstruction of a cube requires 1200 lines from the shadow projection, and the file height is 2000, then these 1200 lines of data from the file are loaded into RAM and cached. Since during the reconstruction of the next cube, most likely, the projection segments will intersect, it will be possible to reuse already downloaded data, loading only new lines.

Server Discovery and Task Distribution

Broadcast UDP packets are used to detect clients and servers. At startup and every 5 seconds, the server sends out such a notification. The client at startup sends out a broadcast request that forces the server to announce itself immediately. The client, having received a notification about the presence of the server, establishes a TCP connection with it, through which control commands, tasks are sent, and notification of completion of the task is received. All clients, servers, tasks have a unique identifier.

When you disconnect from one server, it is assumed that the server has stopped and its tasks are redistributed among others. When a new server is connected, tasks from others are not selected and are not redirected to it. Therefore, for uniform loading, it is important to detect all the servers at the beginning of the distribution of reconstruction tasks. As the cubes are ready, it becomes possible to start the unification tasks. Tasks are sent to a random server. Reconstruction and integration tasks are performed by servers in parallel.

Tasks can come from multiple clients. The server processes them in the order received (FIFO). The client prefers to distribute reconstruction tasks from one layer of unit cubes to one server in order to reduce the amount of data needed by the reconstruction server. The amount of server RAM determines the strategy for reconstructing and compressing cubes. If there is a lot of memory (more than 20 GB), then the compression of the previous cube and reconstruction of the next are carried out in parallel, otherwise the reconstruction of the next cube does not start until the cube is completely processed, i.e. compressed and saved to disk.

The main steps of the reconstruction

First, the projection segments are determined into which the reconstructed volume is projected taking into account the perspective. Based on these data, it is determined which projections are needed for reconstruction. If there are file segments in the RAM cache that are not included in this list, then they are deleted from memory.

The reconstruction stream goes to the cache for the projection segment, the memory block containing the projection (taking into account the page size of 4096 bytes) is locked in memory, which prohibits its upload to the swap, and the pointer is passed to the CUDA procedure. All further actions occur in the memory of the accelerator. Unpacking from 12 bits to float occurs, then all calculations are carried out in float. When unpacking, the segment is cut left and right to the width of the reconstructed block plus the gap required for convolution when filtering the projection. Pre-processing takes place: inversion, gamma correction, averaged projection filtering, the required number of smoothing iterations. Then a convolution takes place, and the segment is once again cut to the left and to the right to the minimum width necessary for reverse projection. This is how projections are processed while there is enough memory on the video card. Those.

The essence of reverse projection is to sum for each voxel from all projections the weight of the point at which the beam of the x-ray source was incident. One call to the CUDA kernel calculates over 32 voxels located one above the other. In this case, a cycle is made for all projection segments loaded into memory. This allows you to store all intermediate data in registers and not to make intermediate entries in memory. At the end of the calculations, the value of the voxel density is recorded in memory. The back projection kernel has 2 implementations, one slow with checks that there is a point on the projection from which to take data, because at the ends of the projections there is not always a point where the value comes from. A quick implementation performs no checks. The desired implementation is automatically selected. The selection of values ​​from the projection is performed according to the algorithm of "nearest neighbor".

If there is insufficient memory, then iterations may require several iterations of projection loading and reverse projection.

Upon completion of the calculations, an assessment of the obtained voxels is made. The maximum and minimum density values ​​are considered, a histogram is built. Building a histogram and copying the results to RAM is done in parallel.

If there are several CUDA devices, segments of the reconstructed cube are processed in parallel. Upon completion of the reconstruction of the cube, another stream begins to compress the cube, and the reconstruction stream is immediately taken for the next task, provided that there is enough RAM. As it turned out, the allocation and freeing of large segments of memory is a very time-consuming operation, therefore all received large blocks of memory are reused. So on CUDA, memory is allocated for a block of voxels, several intermediate buffers, and the rest of the memory is allocated for projections, and the placement of projections in it is controlled manually.

Compression

Compression in the octree is done in several threads. The number of threads depends on the number of processor cores. Each thread processes its octant. Next, the file is saved to the file that was specified by the reconstruction client in the task, and a notification is sent that the cube processing has been completed.

Client

The client maintains the dice database as an SQLite file. It stores the characteristics of cubes, reconstruction time, etc. Upon completion of the reconstruction, the client program is closed, so you can organize batch reconstruction tasks.

CUDA Code Example

The kernel (measureModel.cu), which makes the first pass when calculating the histogram. The file is shown to show the general appearance of the CUDA code in a real working project.

#include 
#include 
#include 
#include 
#include "CudaUtils.h"
#include "measureModel.h"
#define nullptr NULL
struct MinAndMaxValue
{
  float minValue;
  float maxValue;
};
__global__ void
cudaMeasureCubeKernel(float* src, MinAndMaxValue* dst, int ySize, int sliceSize, int blocksPerGridX)
{
  int x = blockDim.x * blockIdx.x + threadIdx.x;
  int z = blockDim.y * blockIdx.y + threadIdx.y;
  int indx = z * blocksPerGridX * blockDim.x + x;
  MinAndMaxValue v;
  v.minValue = src[indx];
  v.maxValue = v.minValue;
  //indx += sliceSize;
  for (int i = 0; i < ySize; ++i)
  {
    float val = src[indx];
    indx += sliceSize;
    if (v.minValue > val)
    v.minValue = val;
    if (v.maxValue < val)
    v.maxValue = val;
  }
  //помещаем данные по нашей строке в разделяемую память
  __shared__ MinAndMaxValue tmp[16][16];
  tmp[threadIdx.y][threadIdx.x] = v;
  //все нити нашего блока посчитали свои значения
  __syncthreads();
  if (threadIdx.y == 0)
  {//первой строкой потоков делаем свертывание временных данных до 16 значений
    for (int i = 0; i < blockDim.y; i++)
    {
      if (v.minValue > tmp[i][threadIdx.x].minValue)
      v.minValue = tmp[i][threadIdx.x].minValue;
      if (v.maxValue < tmp[i][threadIdx.x].maxValue)
      v.maxValue = tmp[i][threadIdx.x].maxValue;
    }
    tmp[0][threadIdx.x] = v;
  }
  __syncthreads();
  ///делаем сверку до одного значения
  if (threadIdx.x == 0 && threadIdx.y == 0)
  {
    for (int i = 0; i < blockDim.y; i++)
    {
      if (v.minValue > tmp[0][i].minValue)
      v.minValue = tmp[0][i].minValue;
      if (v.maxValue < tmp[0][i].maxValue)
        v.maxValue = tmp[0][i].maxValue;
    }
    dst[blockIdx.y * blocksPerGridX + blockIdx.x] = v;
  }
}
void Xrmt::Cuda::CudaMeasureCube(MeasureCubeParams ¶ms)
{
  //будем делать расчеты квадаратными блоками по 256 потока
  int threadsPerBlockX = 16;
  int threadsPerBlockZ = 16;
  int blocksPerGridX = (params.xSize + threadsPerBlockX - 1) / threadsPerBlockX;
  int blocksPerGridZ = (params.zSize + threadsPerBlockZ - 1) / threadsPerBlockZ;
  int blockCount = blocksPerGridX * blocksPerGridZ;
  dim3 threadDim(threadsPerBlockX, threadsPerBlockZ);
  //размер грида
  dim3 gridDim(blocksPerGridX, blocksPerGridZ);
  MinAndMaxValue *d_result = nullptr;
  size_t size = blockCount * sizeof(MinAndMaxValue);
  checkCudaErrors(cudaMalloc( (void**) &d_result, size));
  cudaMeasureCubeKernel<<>>(
    params.d_src,
    d_result,
    params.ySize,
    params.xSize * params.zSize,
    blocksPerGridX
  );
  checkCudaErrors(cudaDeviceSynchronize());
  MinAndMaxValue *result = new MinAndMaxValue[blockCount];
  checkCudaErrors(cudaMemcpy(result, d_result, size, cudaMemcpyDeviceToHost));
  params.maxValue = result[0].maxValue;
  params.minValue = result[0].minValue;
  for (int i = 1; i < blockCount; i++)
  {
    params.maxValue = std::max(params.maxValue, result[i].maxValue);
    params.minValue = std::min(params.minValue, result[i].minValue);
  }
  checkCudaErrors(cudaFree(d_result));
}
__global__ void
cudaCropDensityKernel(float* src, int xSize, int ySize, int sliceSize, float minDensity, float maxDensity)
{
  int x = blockDim.x * blockIdx.x + threadIdx.x;
  int z = blockDim.y * blockIdx.y + threadIdx.y;
  int indx = z * xSize + x;
  for (int i = 0; i < ySize; ++i)
  {
    float val = src[indx];
    if (val < minDensity)
    src[indx] = 0;
    else if (val > maxDensity)
    src[indx] = maxDensity;
    indx += sliceSize;
  }
}
void Xrmt::Cuda::CudaPostProcessCube(PostProcessCubeParams ¶ms)
{
  //будем делать расчеты квадаратными блоками по 256 потока
  int threadsPerBlockX = 16;
  int threadsPerBlockZ = 16;
  int blocksPerGridX = (params.xSize + threadsPerBlockX - 1) / threadsPerBlockX;
  int blocksPerGridZ = (params.zSize + threadsPerBlockZ - 1) / threadsPerBlockZ;
  dim3 threadDim(threadsPerBlockX, threadsPerBlockZ);
  //размер грида
  dim3 gridDim(blocksPerGridX, blocksPerGridZ);
  cudaCropDensityKernel<<>>(
    params.d_src,
    params.xSize,
    params.ySize,
    params.xSize * params.zSize,
    params.minDensity,
    params.maxDensity
  );
  checkCudaErrors(cudaDeviceSynchronize());
}
//на сколько частей делим единицу
#define DivideCount 8
#define ValuesPerThread 32
#define SplitCount 16
#define SplitCount2 64
__global__ void
cudaBuildGistogramKernel(
  float *src, 
  int count, 
  int *d_values,
  int minValue,
  int barCount
)
{
  //индекс значения, начиная с которого считаем
  int barFrom = threadIdx.x * ValuesPerThread;
  int blockIndx = SplitCount * blockIdx.x + threadIdx.y;
  int blockLen = count / (SplitCount * SplitCount2);
  unsigned int values[ValuesPerThread];
  for (int i = 0; i < ValuesPerThread; i++)
  {
    values[i] = 0;
  }
  src += blockLen * blockIndx;
  for(int i = blockLen - 1; i >= 0; i--)
  {
    float v = src[i];
    int indx = (int)((v - (float)minValue) * DivideCount) - barFrom;
    if (indx >= 0 && indx < ValuesPerThread)
      values[indx]++;
  }
  for (int i = 0; i < ValuesPerThread; i++)
  {
    d_values[blockIndx * barCount + barFrom + i] = values[i];
  }
}
__global__ void
cudaSumGistogramKernel(
  int *d_values,
  int barCount
)
{
  //индекс столбика, который суммируем
  int barIndx = blockIdx.x * ValuesPerThread + threadIdx.x;
  unsigned int sum = 0;
  d_values += barIndx;
  for (int i = 0 ; i < SplitCount * SplitCount2; i++)
  {
    sum += d_values[i * barCount];
  }
  d_values[0] = sum;
}
void Xrmt::Cuda::CudaBuildGistogram(BuildGistogramParams ¶ms)
{
  checkCudaErrors(cudaMemcpyAsync(
  params.h_dst, params.d_src, params.count * sizeof(float), cudaMemcpyDeviceToHost, 0
));
  //определяем минимальное значение в гистограмме
  int minValue = (int)(params.minDensity - 1);// для отрицательных значений отбрасывается дробная часть, а этого не достаточно!
  minValue = std::max(minValue, -200);
  //максимальное значение в гистограмме
  int maxValue = (int)params.maxDensity;
  maxValue = std::min(maxValue, 200);
  //количество столбиков в гистограмме (диапазон в 1 делим на DivideCount частей)
  int barCount = (maxValue - minValue + 1) * DivideCount;
  ///делаем количество столбиков кратным ValuesPerThread
  int x32 = barCount % ValuesPerThread;
  barCount += (x32 == 0) ? 0 : ValuesPerThread - x32;
  ///настройка потоков:
  /// x - каждый поток считает 32 столбика, т.е. x пропорционален ширине гистограммы
  /// y - делим блок данных на SplitCount частей
  dim3 threadDim(barCount / 32, SplitCount);
  ///размер грида, делим все данные на SplitCount2 частей
  dim3 gridDim(SplitCount2);
  ///таким образом все данные делим по блокам на SplitCount2 * SplitCount частей
  ///каждую такую часть будет обрабатывать barCount / 32 потоков
  ///резервируем память для хранения промежуточных результатов
  int *d_values = nullptr;
  ///для каждого блока свои значения
  size_t blockValuesCount = SplitCount2 * SplitCount * barCount;
  size_t d_size = blockValuesCount * sizeof(int);
  checkCudaErrors(cudaMalloc( (void**) &d_values, d_size));
  ///выполняем обработку по блокам
  cudaBuildGistogramKernel<<>>(
    params.d_src,
    params.count,
    d_values,
    minValue,
    barCount
  );
  //суммируем блоки на GPU
  cudaSumGistogramKernel<<>>(
    d_values,
    barCount
  );
  checkCudaErrors(cudaDeviceSynchronize());
  //получаем значения гистограммы
  params.histogramValues.resize(barCount);
  checkCudaErrors(cudaMemcpy(
    ¶ms.histogramValues[0], 
    d_values, 
    barCount * sizeof(int), 
    cudaMemcpyDeviceToHost
  ));
  checkCudaErrors(cudaFree(d_values)); 
  params.histogramStep = 1.0 / DivideCount;
  params.histogramStart = (float)minValue;
}

Question number 2

The camera that you used (PIXIS-XF, presumably) gives 2048x2048 pictures, and in the article you write "up to 8000x8000". How did you get it? Do you also move the sample or camera vertically and horizontally and then glue the pictures? AndreyDmitriev

Yes, the PIXIS-XF: 2048B camera was used in the micro tomograph. The reconstruction size according to the statement of work is 8000x8000x20000, the width and depth of 8000 means that the camera sees only part of the image, but is reconstructed more, this gives a decrease in the quality of reconstruction at the edges. The table simply moves in height, a new reconstruction is done, and the results are glued together.

Question number 3

Demo images, which in the video at the end of the article, are all obtained from 360 projections? If so, then this is good, because 360 ​​projections in increments of a degree is quite small, usually they go in increments of a third / quarter of a degree, otherwise there will be reconstruction artifacts. It seems that there is a formula for the optimal number of projections for a given resolution, but I forgot it. AndreyDmitriev

In our case, 180-360 projections were used. Different algorithms can give different quality of reconstructions depending on the number of projections, but in general, the rule is fulfilled that with an increase in the number of projections, the quality increases. For our tasks it was enough to use 180-360 projections to get good quality.

The algorithm normally responds to skipping frames at the cost of a slight decrease in resolution in the direction where there are gaps. In addition, the camera had the peculiarity of overheating, and its “brightness” floated, so part of the frames were discarded as defective, the rest were normalized to average brightness.

Question number 4

I also did not really understand about the frequency of the camera. According to the specification, it is dual-frequency at 100 kilohertz or two megahertz. If she has four megapixels, does this mean that she gives a frame every two seconds at maximum frequency? AndreyDmitriev

Yes, you are right.
According to the camera’s documentation , the frequency characteristics are as follows: ADC speed / bits 100 kHz / 16-bit and 2 MHz / 16-bit

That is, if one point of the image has a resolution of 16 bits, we get that the frequency for the whole image will be: 2000000 / (2048 * 2048) = 0.47 hertz

Question number 5

Do you move the manipulator step by step or continuously? How long does it take to scan typical samples that are presented in the video? AndreyDmitriev

Manipulator (table) moves in steps. They turned a corner, stopped, shot, turned again, etc.
The average scan time is 11 minutes at 378 frames.

Question number 6

Well, about 12 bits - very interesting. The fact that you can cut four bits and pack every two pixels into three bytes is possible for storage and transmission - this is understandable. But for reconstruction you have to deploy each pixel again at least two bytes? Or do you have all the math on 12 bits? In this case, how did you solve the problem that pixels occupy one and a half bytes and do not align to the border? AndreyDmitriev

File format of 12 bit side projections.

1. Pixels are bitwise packed and arranged in lines, so that two points occupy 3 bytes, and it is assumed that the width of the projection image is a multiple of 2, according to the formula: lineWidthInBytes = width () * 3/2.
2. Usually, the entire amount of data is not loaded at once, but “windows” are used, into which only the necessary portion of the image is loaded, and it is assumed that the left and right borders are aligned by a multiple of four pixels.
3. After loading the “window”, further work is carried out using the functions of full import / export of this window into arrays of the float or quint16 type. In the process of import / export, a conversion from 12 bits to the required bit depth occurs.
4. In our case, the gain from reducing the size of projection files was greater than the loss of performance in this case. In addition, since the files were not completely downloaded, but only “windows” intended for processing on a particular cluster machine, the performance loss is even less due to the parallelization of tasks.

Real-time volumetric (voxel) rendering

An interesting task was to display the model using voxels in real time. In addition to the voxels of the model itself, it was necessary to display in 3D such tools as a bounding box, a secant plane, hide half of the object along the secant plane, and also hide the object outside the parallelepiped. The user interface element is displayed on the cutting plane in the form of a “lever” (which at the same time corresponds to the normal vector), which allows you to move the projection slice window along the cutting plane and to shift the plane along the normal vector. The projection slice window can also be stretched beyond its borders and rotated. On the bounding box, in addition to its edges, the same "levers" are displayed as on the plane, which also allow you to change its size.

A sufficient frame rate during operation was provided due to the dynamic level of detail, since data loading occurs automatically when the bounding box is reduced.

For manipulating interface elements in 3D, special sets of mathematical functions were implemented. The initial creation of a secant plane, if described in general terms without using formulas, looks something like this: the user double-clicks at any point in the model, after which this point is fixed, and from it with a further movement of the mouse the normal vector to the plane being created is displayed. In this case, in fact, the plane has already been created, and it lies on the beam coming from the screen coordinates of the mouse cursor deep into space, not parallel to the perspective lines, so that the beam is projected like a dot on the screen, and the orientation of the plane changes dynamically when the mouse moves, and the user sees this right on the screen. To complete the creation, click the mouse again to fix the orientation of the plane.

In addition to the elements of model manipulation, there are tools in the volume to control the color spectra of densities and transparency levels.

The voxel itself and cropping by the secant plane and bounding box were directly implemented using the VTK library.

List of Math Functions

Mathematical classes and functions used for geometric calculations in the project.
1. The class of the plane .

• Description of the plane along the normal and the point .
• Three point description .
• The rotation angle of the 2D coordinate system inside the plane around the normal vector.
• Indentation of the boundaries of a 2D rectangular region inside a plane with a reference point on the normal vector.
• Functions of transition from a 2D point inside a plane rotated around a normal to real 3D coordinates and inverse transformation.

2. A set of mathematical functions for geometric calculations.

• Obtaining on the basis of a vector of two vectors mutually perpendicular and perpendicular to the original vector .
• Getting a vector perpendicular to a given vector in a 2D coordinate system .
• Defining an octant in the direction of the vector and vice versa creating a vector in the octant.
• Correction of the central point of the plane to position it inside the bounding box.
• Checking the entry of a point in the box.
• The intersection of the beam and the plane .
• The intersection of a segment and a plane.
• The distance of a point from a line .
• The perpendicular vector to the line from an arbitrary point to a point on the line .
• The distance from a point to a plane .
• The projection of a point onto a plane .
• Vector projection on vector .
• The angle between the 2D vectors .

3. Mathematical functions used in the reconstruction.

• Inversion.
• Gamma correction .
• Filtration by averaged projection.
• The required number of smoothing iterations .
• Convolution.

More projects:
How to create software for the
SDK microtomograph for 5233 man-hours to implement support for e-books in the FB2 format
Managing access to electronic documents. From DefView to Vivaldi We
integrate two video surveillance systems: Axxon Next and SureView.
More about the development of software for X-ray tomograph
“Sphere”: how to monitor billions of kilowatt hours.
Developing a simple plug-in for JIRA to work with the database.
To help DevOps: firmware builder for network devices on Debian for 1008 hours
Auto-update Windows service through AWS for the poor