Source : Wikipedia License CC-BY-SA 3.0

If you often travel by public transport, you probably encountered the following situation:

You come to a halt. It is written that the bus runs every 10 minutes. Notice the time ... Finally, after 11 minutes, the bus comes and thought: why do I always have bad luck?

In theory, if the buses arrive every 10 minutes, and you arrive at a random time, then the average wait should be about 5 minutes. But in reality, buses do not arrive right on schedule, so you can wait longer. It turns out that with some reasonable assumptions you can come to a striking conclusion:

When you wait for a bus, which comes on average every 10 minutes, your average waiting time will be 10 minutes.

This is what is sometimes called the waiting time paradox .

I had met the idea before, and I always wondered if it really was true ... how much did such “reasonable assumptions” correspond to reality? In this article, we explore the waiting time paradox in terms of both modeling and probabilistic arguments, and then take a look at some real-world data from the buses in Seattle to (hopefully) solve the paradox once and for all.

Paradox Inspection

If buses arrive exactly every ten minutes, then the average waiting time is really 5 minutes. It is easy to see why adding variations in the interval between buses increases the average waiting time.

The waiting time paradox is a special case of a more general phenomenon — the inspection paradox , which is discussed in detail in Allen Downey ’s sensible article, “The Paradox of Inspection All Around Us” .

In short, the inspection paradox occurs whenever the probability of seeing a quantity is related to the quantity observed. Allen gives an example of a survey of university students about the average size of their classes. Although the school truly speaks of an average of 30 students per group, but the average group sizefrom the students point of view, much more. The reason is that in large classes (naturally) there are more students, which is revealed when they are surveyed.

In the case of a bus schedule with a stated 10-minute interval, sometimes the interval between arrivals is longer than 10 minutes, and sometimes shorter. And if you come to a stop at a random time, then you are more likely to encounter a longer interval than a shorter one. Therefore, it is logical that the average time interval between waiting intervals is longer than the average time interval between buses, because longer intervals are more often found in the sample.

But the waiting time paradox makes a stronger statement: if the average interval between buses is$$minutes, the average waiting time for passengers is$$minutes Could this be true?

Imitation of waiting time

To convince ourselves of the rationality of this, we first model the flow of buses that arrive on average in 10 minutes. For accuracy, take a large sample: a million buses (or about 19 years of around-the-clock 10-minute traffic):

import numpy as np
N = 1000000# number of buses
tau = 10# average minutes between arrivals
rand = np.random.RandomState(42)  # universal random seed
bus_arrival_times = N * tau * np.sort(rand.rand(N))

Check that the average interval is close to $$:

intervals = np.diff(bus_arrival_times)
intervals.mean()

9.9999879601518398

Now we can simulate the arrival of a large number of passengers at the bus stop during this period of time and calculate the waiting time that each of them experiences. Encapsulate the code in a function for later use:

defsimulate_wait_times(arrival_times,
                        rseed=8675309,  # Jenny's random seed
                        n_passengers=1000000):
    rand = np.random.RandomState(rseed)
    arrival_times = np.asarray(arrival_times)
    passenger_times = arrival_times.max() * rand.rand(n_passengers)
    # find the index of the next bus for each simulated passenger
    i = np.searchsorted(arrival_times, passenger_times, side='right')
    return arrival_times[i] - passenger_times

Then simulate the wait time and calculate the average:

wait_times = simulate_wait_times(bus_arrival_times)
wait_times.mean()

10.001584206227317

The average waiting time is close to 10 minutes, as predicted by the paradox.

Digging deeper: probabilities and Poisson processes

How to simulate such a situation?

In essence, this is an example of the inspection paradox, where the probability of observing a value is related to the value itself. Denote by$$ spacing $$between the buses as they arrive at the bus stop. In such a record, the expected arrival time will be:

$$

In the previous simulation we chose $$minutes

When a passenger arrives at a bus stop at an arbitrary time, the probability of waiting time will depend not only on$$but also from the very $$: the greater the interval, the more passengers in it.

Thus, you can write the distribution of arrival time from the point of view of passengers:

$$

The proportionality constant is derived from the normalization of the distribution:

$$

It is simplified to

$$

Then wait time $$ will be half the expected interval for passengers, so we can write

$$

which can be rewritten in a more understandable way:

$$

and now it remains only to choose a form for $$ and calculate integrals.

Choice of p (t)

Having a formal model, what is a reasonable distribution for $$? Let's display a picture of the distribution$$ within our simulated arrivals by plotting a histogram of the intervals between arrivals:

%matplotlib inline
import matplotlib.pyplot as plt
plt.style.use('seaborn')
plt.hist(intervals, bins=np.arange(80), density=True)
plt.axvline(intervals.mean(), color='black', linestyle='dotted')
plt.xlabel('Interval between arrivals (minutes)')
plt.ylabel('Probability density');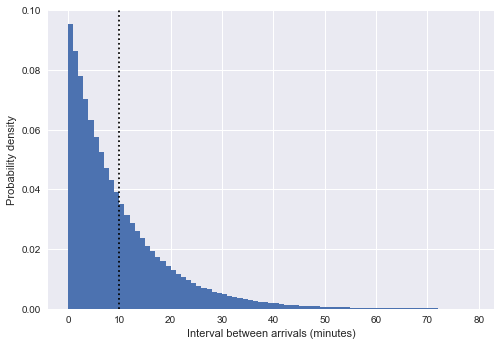

Here the vertical dotted line shows the average interval of about 10 minutes. This is very similar to the exponential distribution, and not by chance: our simulation of the bus arrival time in the form of uniform random numbers is very close to the Poisson process , and for such a process the distribution of intervals is exponential.

(Note: in our case, this is only an approximate exponent; in fact, the intervals$$ between $$ uniformly selected points within a period of time $$match beta distribution$$which is a big limit $$ approaching $$. For more information, you can read, for example, a post on StackExchange or this thread on Twitter ).

The exponential distribution of intervals implies that the arrival time follows the Poisson process. To test this reasoning, we check the existence of another property of the Poisson process: that the number of arrivals during a fixed period of time is a Poisson distribution. To do this, we divide the simulated arrival to the hourly blocks:

from scipy.stats import poisson
# count the number of arrivals in 1-hour bins
binsize = 60
binned_arrivals = np.bincount((bus_arrival_times // binsize).astype(int))
x = np.arange(20)
# plot the results
plt.hist(binned_arrivals, bins=x - 0.5, density=True, alpha=0.5, label='simulation')
plt.plot(x, poisson(binsize / tau).pmf(x), 'ok', label='Poisson prediction')
plt.xlabel('Number of arrivals per hour')
plt.ylabel('frequency')
plt.legend();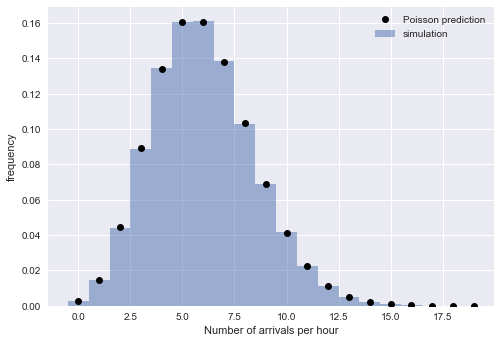

The close correspondence between empirical and theoretical values ​​confirms the correctness of our interpretation: for large $$The simulated arrival time is well described by the Poisson process, which implies exponentially distributed intervals.

This means that you can write the probability distribution:

$$

If we substitute the result in the previous formula, we will find the average waiting time for passengers at the bus stop:

$$

For flights arriving with the Poisson process, the expected waiting time is identical to the average interval between arrivals. One

can argue about this problem as follows: the Poisson process is a process without memory , that is, the event history has nothing to do with the expected time of the next event. Therefore, on arrival at the bus stop, the average waiting time for the bus is always the same: in our case it is 10 minutes, no matter how much time has passed since the previous bus! It does not matter how long you waited: the expected time until the next bus is always exactly 10 minutes: in the Poisson process you do not get a “credit” for the time spent waiting.

Waiting time in reality

The above is good if real bus arrivals are actually described by the Poisson process, but is it?


Source: Seattle's public transport scheme.

Let's try to determine how the waiting time paradox agrees with reality. To do this, let's examine some of the data available for download here: arrival_times.csv (CSV file of 3 MB). The dataset contains scheduled and actual arrival times for RapidRide C, D, and E buses at the 3rd & Pike bus stop in downtown Seattle. The data was recorded in the second quarter of 2016 (many thanks to Mark Hallenbek from the Washington State Transportation Center for this file!).

import pandas as pd
df = pd.read_csv('arrival_times.csv')
df = df.dropna(axis=0, how='any')
df.head()

	OPD_DATE	VEHICLE_ID	RTE	DIR	TRIP_ID	STOP_ID	STOP_NAME	SCH_STOP_TM	ACT_STOP_TM
0	2016-03-26	6201	673	S	30908177	431	3RD AVE & PIKE ST (431)	01:11:57	01:13:19
one	2016-03-26	6201	673	S	30908033	431	3RD AVE & PIKE ST (431)	23:19:57	23:16:13
2	2016-03-26	6201	673	S	30908028	431	3RD AVE & PIKE ST (431)	21:19:57	21:18:46
3	2016-03-26	6201	673	S	30908019	431	3RD AVE & PIKE ST (431)	19:04:57	19:01:49
four	2016-03-26	6201	673	S	30908252	431	3RD AVE & PIKE ST (431)	16:42:57	16:42:39

I chose RapidRide data also because for most of the day buses run at regular intervals of 10-15 minutes, not to mention that I am a frequent passenger of route C.

Data cleansing

To begin with, we will do a little data cleaning to convert them to a convenient form:

# combine date and time into a single timestamp
df['scheduled'] = pd.to_datetime(df['OPD_DATE'] + ' ' + df['SCH_STOP_TM'])
df['actual'] = pd.to_datetime(df['OPD_DATE'] + ' ' + df['ACT_STOP_TM'])
# if scheduled & actual span midnight, then the actual day needs to be adjusted
minute = np.timedelta64(1, 'm')
hour = 60 * minute
diff_hrs = (df['actual'] - df['scheduled']) / hour
df.loc[diff_hrs > 20, 'actual'] -= 24 * hour
df.loc[diff_hrs < -20, 'actual'] += 24 * hour
df['minutes_late'] = (df['actual'] - df['scheduled']) / minute
# map internal route codes to external route letters
df['route'] = df['RTE'].replace({673: 'C', 674: 'D', 675: 'E'}).astype('category')
df['direction'] = df['DIR'].replace({'N': 'northbound', 'S': 'southbound'}).astype('category')
# extract useful columns
df = df[['route', 'direction', 'scheduled', 'actual', 'minutes_late']].copy()
df.head()

	Route	Direction	Schedule	Fact. arrival	Lateness (min)
0	C	south	2016-03-26 01:11:57	2016-03-26 01:13:19	1.366667
one	C	south	2016-03-26 23:19:57	2016-03-26 23:16:13	-3.733333
2	C	south	2016-03-26 21:19:57	2016-03-26 21:18:46	-1.133333
3	C	south	2016-03-26 19:04:57	2016-03-26 19:01:49	-3.133333
four	C	south	2016-03-26 16:42:57	2016-03-26 16:42:39	-0.300000

How late are the buses?

There are six data sets in this table: north and south directions for each route C, D and E. To get an idea of ​​their characteristics, let's build a histogram of the actual minus of the planned arrival time for each of these six:

import seaborn as sns
g = sns.FacetGrid(df, row="direction", col="route")
g.map(plt.hist, "minutes_late", bins=np.arange(-10, 20))
g.set_titles('{col_name} {row_name}')
g.set_axis_labels('minutes late', 'number of buses');

It is logical to assume that the buses closer to the schedule at the beginning of the route and more deviate from it to the end. The data confirms this: our stop on the southern route C, as well as on the northern D and E is close to the beginning of the route, and in the opposite direction - close to the final destination.

Scheduled and Observed Intervals

Look at the observed and planned intervals between buses for these six routes. Let's start with the function groupbyin Pandas to calculate these intervals:

defcompute_headway(scheduled):
    minute = np.timedelta64(1, 'm')
    return scheduled.sort_values().diff() / minute
grouped = df.groupby(['route', 'direction'])
df['actual_interval'] = grouped['actual'].transform(compute_headway)
df['scheduled_interval'] = grouped['scheduled'].transform(compute_headway)

g = sns.FacetGrid(df.dropna(), row="direction", col="route")
g.map(plt.hist, "actual_interval", bins=np.arange(50) + 0.5)
g.set_titles('{col_name} {row_name}')
g.set_axis_labels('actual interval (minutes)', 'number of buses');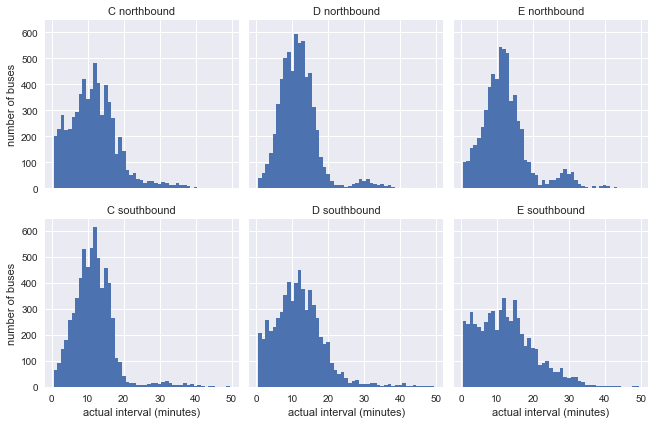

It can already be seen that the results are not very similar to the exponential distribution of our model, but this still does not say anything: non-constant intervals in the graph can affect the distribution.

Repeat the construction of the diagrams, taking the planned, rather than the observed arrival intervals:

g = sns.FacetGrid(df.dropna(), row="direction", col="route")
g.map(plt.hist, "scheduled_interval", bins=np.arange(20) - 0.5)
g.set_titles('{col_name} {row_name}')
g.set_axis_labels('scheduled interval (minutes)', 'frequency');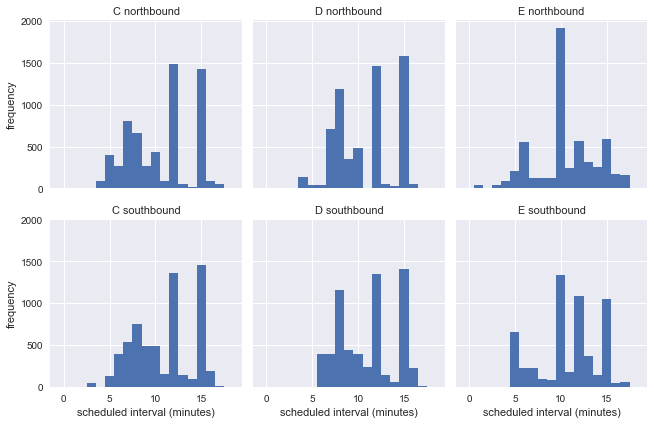

This shows that during the week buses run at different intervals, so that we cannot assess the accuracy of the waiting time paradox for real information from a stop.

Building uniform schedules

Although the official schedule does not give uniform intervals, there are several specific time intervals with a large number of buses: for example, almost 2000 buses of route E to the north side with a scheduled interval of 10 minutes. To find out if the wait time paradox is applicable, let's group the data by route, route, and planned interval, and then re-add it as if it happened sequentially. This should preserve all relevant characteristics of the source data, while making it easier to compare directly with the predictions of the waiting time paradox.

defstack_sequence(data):# first, sort by scheduled time
    data = data.sort_values('scheduled')
    # re-stack data & recompute relevant quantities
    data['scheduled'] = data['scheduled_interval'].cumsum()
    data['actual'] = data['scheduled'] + data['minutes_late']
    data['actual_interval'] = data['actual'].sort_values().diff()
    return data
subset = df[df.scheduled_interval.isin([10, 12, 15])]
grouped = subset.groupby(['route', 'direction', 'scheduled_interval'])
sequenced = grouped.apply(stack_sequence).reset_index(drop=True)
sequenced.head()

	Route	Direction	schedule	Fact. arrival	Lateness (min)	Fact. interval	Schedule interval
0	C	north	10.0	12.400000	2,400,000	NaN	10.0
one	C	north	20.0	27.150000	7.150000	0.183333	10.0
2	C	north	30.0	26.966667	-3.033333	14.566667	10.0
3	C	north	40.0	35.516667	-4.483333	8.366667	10.0
four	C	north	50.0	53.583333	3.583333	18.066667	10.0

On the cleared data, you can make a graph of the distribution of the actual appearance of buses for each route and direction with the frequency of arrival:

for route in ['C', 'D', 'E']:
    g = sns.FacetGrid(sequenced.query(f"route == '{route}'"),
                      row="direction", col="scheduled_interval")
    g.map(plt.hist, "actual_interval", bins=np.arange(40) + 0.5)
    g.set_titles('{row_name} ({col_name:.0f} min)')
    g.set_axis_labels('actual interval (min)', 'count')
    g.fig.set_size_inches(8, 4)
    g.fig.suptitle(f'{route} line', y=1.05, fontsize=14)

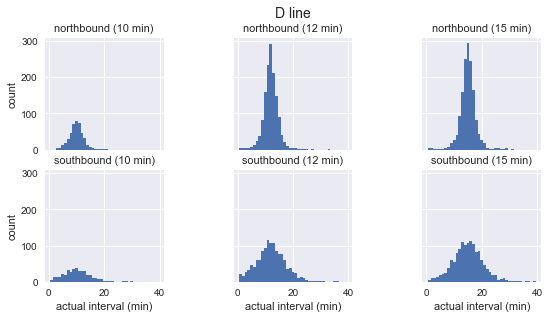
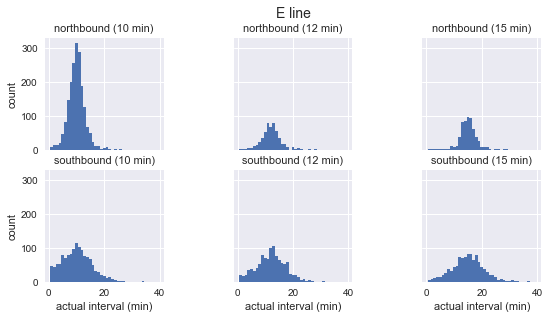
We see that for each route the distribution of the observed intervals is almost Gaussian. It reaches a maximum near the planned interval and has a standard deviation that is less at the beginning of the route (south for C, north for D / E) and more at the end. Even by sight it can be seen that the actual arrival intervals definitely do not correspond to the exponential distribution, which is the basic assumption on which the waiting time paradox is based.

We can take the simulated wait time function that we used above to find the average wait time for each bus route, route, and schedule:

grouped = sequenced.groupby(['route', 'direction', 'scheduled_interval'])
sims = grouped['actual'].apply(simulate_wait_times)
sims.apply(lambda times: "{0:.1f} +/- {1:.1f}".format(times.mean(), times.std()))

route direction scheduled interval
C North 10.0 7.8 +/- 12.5
                      12.0 7.4 +/- 5.7
                      15.0 8.8 +/- 6.4
         South 10.0 6.2 +/- 6.3
                      12.0 6.8 +/- 5.2
                      15.0 8.4 +/- 7.3
D North 10.0 6.1 +/- 7.1
                      12.0 6.5 +/- 4.6
                      15.0 7.9 +/- 5.3
         South 10.0 6.7 +/- 5.3
                      12.0 7.5 +/- 5.9
                      15.0 8.8 +/- 6.5
E North 10.0 5.5 +/- 3.7
                      12.0 6.5 +/- 4.3
                      15.0 7.9 +/- 4.9
         South 10.0 6.8 +/- 5.6
                      12.0 7.3 +/- 5.2
                      15.0 8.7 +/- 6.0
Name: actual, dtype: object

The average wait time is perhaps a minute or two more than half of the planned interval, but not equal to the planned interval, as the waiting time paradox implies. In other words, the inspection paradox is confirmed, but the waiting time paradox is not true.

Conclusion

The waiting time paradox was an interesting starting point for discussion, which included modeling, probability theory, and comparing statistical assumptions with reality. Although we have confirmed that in the real world, bus routes are subject to some kind of inspection paradox, the above analysis quite convincingly shows that the basic assumption underlying the waiting time paradox, that buses arrive, follows statistics from the Poisson process, is not valid.

Looking back, this is not surprising: the Poisson process is a memoryless process, which assumes that the probability of arrival is completely independent of the time since the previous arrival. In fact, in a well-managed public transport system there are specially structured timetables to avoid such behavior: buses do not start their routes at random times during the day, but start according to the schedule chosen for the most efficient transportation of passengers.

The more important lesson is that you should be careful about the assumptions you make to any data mining task. Sometimes the Poisson process is a good description for the arrival time data. But just because one data type sounds like another data type does not mean that the assumptions valid for one are necessarily valid for another. Often, assumptions that seem correct can lead to conclusions that are not true.