Work with data: New science

The volume of scientific data is increasing at an astonishing rate, so there is a need for new mathematical methods and methods of analysis. Datasets are becoming more and more complex in many disciplines related, for example, to neural networks, astrophysics or medicine.

Physicist from Northeastern University (USA) Alessandro Vespignani (Alessandro Vespignani) is engaged in modeling the behavior of the stock market, predicting election results and other statistical problems. He has at his disposal several terabytes of data received from social networks, and almost all of them [data] are unstructured.

Vespignani uses a wide range of mathematical tools and methods to process the collected data. He sorts millions of tweets and searches for keywords. Vespignani effectively takes a phased approach to big data analysis. However, Ronald Coifman, a mathematician at Yale University, argues that it is not enough just to collect and store huge amounts of information, they need to be properly organized, and this requires a special structure.

Vertices and ribs

The city of Königsberg (now Kaliningrad), which arose in the 13th century, consisted of three formally independent urban settlements, which were located on the islands and banks of the Pregol River, dividing the city into four main parts. These four plots of land were interconnected by seven bridges. In the 18th century, the mathematician Leonhard Euler puzzled over a riddle that was popular at that time: how to get across all seven bridges of Königsberg and return to the starting point without stepping on each of the bridges twice?

To solve it, Euler built a model from points and lines and found that the problem has a solution only if an even number of bridges lead to each "island of the earth". Since there were an odd number of bridges in Königsberg, this journey was not possible.

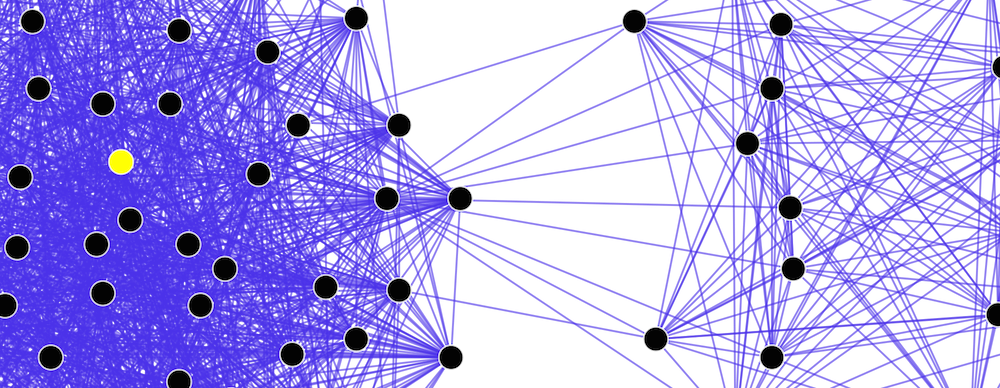
Building on Euler’s idea, Stanford University mathematician Gunnar Carlsson began building data maps, representing cumbersome datasets as a network of vertices and edges. The approach is called Topological Data Analysis (TDA), and, according to Gunnar, "allows you to structure unstructured data so that you can later analyze it using machine learning methods." In the video, Karlsson explains how topological analysis helps researchers interpret large data sets.

As in the case of the puzzle about bridges, everything here is “connected” with connections, sorry for the pun. Social networks are a map of relationships between people, where the vertices are names and the edges are connections. Karlsson believes that this approach can be used in other areas, for example, to work with genomic sequences. “You can compare the sequences and identify the number of differences. The resulting number can be represented as a function of distance, which will show how much they differ, ”Karlsson explains.

The Carlsson Ayasdi project was created for this: it simplifies the presentation of high-dimensional data. If your multidimensional data set has 155 variables, then what will the query look like, taking them all into account at once? Karlsson compares this task to finding a hammer in a dark garage. If you have a flashlight, then you will sequentially look through the contents of the garage until you come across the tool you need - this process is quite long and can make you crazy. It is much more efficient to turn on the light - you will immediately find both a hammer and a box of nails, although you did not suspect that you would need them. Ayasdi technology just lights a bulb.

Using topological methods, we are as if projecting a complex object onto a plane. The danger is that some patterns are likeillusions in the theater of shadows, and in fact do not exist. Moreover, a number of scientists believe that topological methods are generally not applicable to some data sets. If your data set is distorted or incomplete, then they can give completely incorrect results.

Occam's razor

In February 2004, Stanford University mathematician Emmanuel Candes tried to find a way to improve blurry images. Candes applied one of the developed algorithms and expected to see minor improvements, but he had a clear picture. According to Candes, the probability of this was equal to the probability of guessing ten digits of a bank card number, knowing the first three. But that was not an accident. The method worked with other images as well.

The key to success was the mathematical version of Occam's razor, so to speak: of the millions of possible options for reconstructing a particular fuzzy image, the simplest version is best suited. This discovery gave rise to the method of Compressed sensing.

Today it is used in video broadcasts over the network. The amount of data when transmitting video is so huge that you have to compress it. Usually, in order to compress data, you must first get all the bits, and then discard the insignificant. The Compressed sensing method allows you to determine significant bits without requiring their preservation.

“If I screen a population for a rare disease, do I need blood tests for all people? The answer is no. It is enough to conduct only a few tests, because the desired “factor” is very rare, that is, it is sparse, ”said Candes. Suppose we have one infected in a group of 32 people. We took blood from each of them for analysis. If the test is negative, then there are no infected. But if the result is positive, then how to find the infected?

Candes believes that you can take half the samples (16) and re-analyze. If the result is positive, then the infected person is in this group, if not, then in another. Then the group is again divided in half, and testing is repeated. Thus, you will get the answer for 5 tests, instead of 32, if you test each separately. This is the essence of the Compressed sensing method.

Compressed sensing can help with large data sets, some of which have been lost or damaged. A good example would be the processing of medical records, in part of which there are typos made by the personnel of the clinic. Another example is the face recognition system: if a person puts on glasses, he can still be recognized.

While Candes extols Compressed sensing, Karlsson takes a topological approach. However, these two methods only complement each other, but do not compete. “After all, data science is more than just the sum of methodologies,” Vespignani insists. “By combining several methods, we can create something completely new.”

PS More recently, we published a selection of sources for machine learning for beginners and talked about deep learning. Of course, we share our own experience: a little about developing a quantum communication system and how advanced programmers are prepared from ordinary students .