Algorithm for creating a list of all permutations or placements
I’ll make a reservation right away , this article is thematically similar to the “ Non-recursive permutation generation algorithm ” published about a year ago by SemenovVV , but the approach here is, in my opinion, fundamentally different.
I was faced with the need to compile a list of all permutations of n elements. For n = 4 or even 5, the problem is solved manually in a matter of minutes, but for 6! = 720 and above, I was already too lazy to write pages - I needed automation. I was sure that this “bicycle” was already invented many times and in various variations, but it was interesting to figure it out on my own - therefore, deliberately without looking at the relevant literature, I sat down to create an algorithm.
I rejected the first version of the recursive code as being too trivial and resource intensive. Further, having made “feint with ears”, he developed a not very efficient algorithm, sorting out a knowingly larger number of options and filtering out only suitable ones. It worked, but I wanted something elegant - and, starting from scratch, I began to look for patterns in the lexicographic order of permutations for small values of n . The result was a neat code that with minimal “tying” can be represented in Python in 10 lines (see below). Moreover, this approach works not only for permutations, but also for placing n elements at m positions (in the case when, n ≥ m ).
If you look at the list of all permutations for 4 to 4, a certain structure is noticeable:
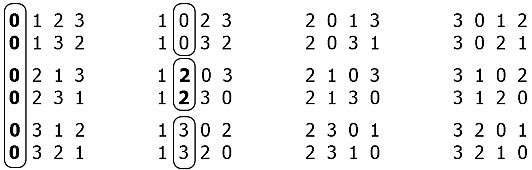
The entire array of permutations (4! = 24) can be divided into groups of (n-1)! = 3! - six permutations, and each group in turn is divided into (n-1-1)! = 2! –Two combinations and so on. In the case considered, when for n = 4, that's all.
So, from the point of view of lexicography, this set of permutations can be thought of as an increasing series: so to speak, 0123 <0132 <... <3210. We know in advance how many times the same element will be repeated in a certain position - this is the number of permutations for the array order less by one, i.e. (a-1)! where a- dimension of the current array. Then a sign of the transition to the next value will be a new result of integer division (" // ") of the sequence number i of the combination by the number of such permutations: i // (a-1)! . Also, to determine what the number of this element will be in the list of not yet used (so as not to iterate over it in a circle), we use the remainder of dividing (“ % ”) the obtained value by the length of this list. T.O. we have the following construction:
i // (a-1)! % r ,
where r is the dimension of the array of elements not yet involved.
For clarity, we consider a specific case. Of all 24 permutations iЄ [0, 23] 4 elements in 4 positions, for example, the 17th will be the following sequence:
[17 // (4-1)!]% R (0,1,2,3) = 2% 4 = 2
(that is, if you count from 0, the third element of the list is “2”). The next element of this permutation will be:
[17 // (3-1)!]% R (0,1,3) = 8% 3 = 2
(again the third element - now it is “3”)
If you continue in the same vein, as a result, we get the array “2 3 1 0”. Therefore, looping through all the values of i from the number of permutations [ n! ] or placements [ n! / (nm)! , where m is the number of positions in the array], we get an exhaustive set of the desired combinations.
Actually, the code itself looks like this:
UPD: over time, I realized that the method is not well tested - therefore, if someone starts using it, please be vigilant (I would not want to let anyone down)
I was faced with the need to compile a list of all permutations of n elements. For n = 4 or even 5, the problem is solved manually in a matter of minutes, but for 6! = 720 and above, I was already too lazy to write pages - I needed automation. I was sure that this “bicycle” was already invented many times and in various variations, but it was interesting to figure it out on my own - therefore, deliberately without looking at the relevant literature, I sat down to create an algorithm.
I rejected the first version of the recursive code as being too trivial and resource intensive. Further, having made “feint with ears”, he developed a not very efficient algorithm, sorting out a knowingly larger number of options and filtering out only suitable ones. It worked, but I wanted something elegant - and, starting from scratch, I began to look for patterns in the lexicographic order of permutations for small values of n . The result was a neat code that with minimal “tying” can be represented in Python in 10 lines (see below). Moreover, this approach works not only for permutations, but also for placing n elements at m positions (in the case when, n ≥ m ).
If you look at the list of all permutations for 4 to 4, a certain structure is noticeable:

The entire array of permutations (4! = 24) can be divided into groups of (n-1)! = 3! - six permutations, and each group in turn is divided into (n-1-1)! = 2! –Two combinations and so on. In the case considered, when for n = 4, that's all.
So, from the point of view of lexicography, this set of permutations can be thought of as an increasing series: so to speak, 0123 <0132 <... <3210. We know in advance how many times the same element will be repeated in a certain position - this is the number of permutations for the array order less by one, i.e. (a-1)! where a- dimension of the current array. Then a sign of the transition to the next value will be a new result of integer division (" // ") of the sequence number i of the combination by the number of such permutations: i // (a-1)! . Also, to determine what the number of this element will be in the list of not yet used (so as not to iterate over it in a circle), we use the remainder of dividing (“ % ”) the obtained value by the length of this list. T.O. we have the following construction:
i // (a-1)! % r ,
where r is the dimension of the array of elements not yet involved.
For clarity, we consider a specific case. Of all 24 permutations iЄ [0, 23] 4 elements in 4 positions, for example, the 17th will be the following sequence:
[17 // (4-1)!]% R (0,1,2,3) = 2% 4 = 2
(that is, if you count from 0, the third element of the list is “2”). The next element of this permutation will be:
[17 // (3-1)!]% R (0,1,3) = 8% 3 = 2
(again the third element - now it is “3”)
If you continue in the same vein, as a result, we get the array “2 3 1 0”. Therefore, looping through all the values of i from the number of permutations [ n! ] or placements [ n! / (nm)! , where m is the number of positions in the array], we get an exhaustive set of the desired combinations.
Actually, the code itself looks like this:
import math
elm=4 # к-во элементов, n
cells=4 # к-во положений, m
res=[] # результирующий список
arrang = math.factorial(elm)/math.factorial(elm-cells) # расчёт к-ва сочетаний
for i in range(arrang):
res.append([])
source=range(elm) # массив ещё не задействованных элементов
for j in range(cells):
p=i//math.factorial(cells-1-j)%len(source)
res[len(res)-1].append(source[p])
source.pop(p)
UPD: over time, I realized that the method is not well tested - therefore, if someone starts using it, please be vigilant (I would not want to let anyone down)
