Fuzzy search in a dictionary with a universal Levenshtein automaton. Part 1
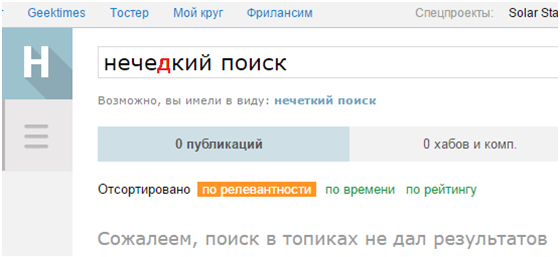
Fuzzy string searching is a very expensive task in terms of computational resources, especially if you need high accuracy of the results. The article describes the fuzzy search algorithm in the dictionary, which provides high search speed while maintaining 100% accuracy and relatively low memory consumption. It was the Levenshtein automaton that allowed Lucene developers to increase the speed of fuzzy search by two orders of magnitude
Introduction
Fuzzy string search in the dictionary is the basis for building modern spell-checking systems, which are used in text editors, optical character recognition systems and search engines. In addition, fuzzy search finds application in solving a number of computational problems of bioinformatics.

A formal definition of a fuzzy search problem in a dictionary can be formulated as follows. For a given search query W, it is necessary to select from the dictionary D a subset P of all words whose measure of difference p from the search query does not exceed a certain threshold value N : The
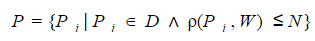
degree of difference of two words can be measured, for example, using distanceLevenshtein or Damerau-Levenshtein .
Levenshtein distance is a measure of the difference between two lines, defined as the minimum number of insertion, deletion and replacement of characters required to translate one line to another.
When calculating the Damerau-Levenshtein distance, transpositions (permutations of two adjacent symbols) are also allowed.
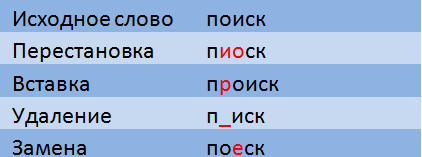
A few years ago on Habré there was already a post from ntz devoted to fuzzy search in the dictionary and text - more about the distances of Levenshtein and Damerau-Levenshtein can be read there. I only recall that the time complexity for checking the condition
p (P i , W) <= N by means of dynamic programming methods is estimated as
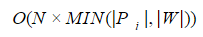 ,
,где |Pi|,|W| — длина строки и запроса соответственно. Поэтому при решении практических задач полный перебор значений словаря с проверкой каждого слова, как правило, неприемлем.
Следует отметить, что не каждый алгоритм нечеткого поиска обеспечивает нахождение по запросу W абсолютно всех слов из словаря D, удовлетворяющих условию р(Pi, W)<=N. Поэтому есть смысл говорить о точности поиска как об отношении количества найденных результатов к действительному количеству слов в словаре, удовлетворяющих заданному условию. Например, точность поиска методом n-грамм автор уже упомянутого мной поста оценил в 65%.
Недетерминированный автомат Левенштейна
The author assumes that the reader is familiar with the basics of the theory of automata and formal languages and will refrain from expounding the terminology of this subject area. Instead, I’ll get down to business right away.
To solve practical problems, a deterministic finite state machine of Levenshtein is used (to be completely accurate, its imitation). However, in order to understand the operating principles of the deterministic finite state machine of Levenshtein, it is better to first consider the operation of the non-deterministic version.
By a Levenshtein automaton for a word W we mean a finite automaton A N (W) that takes a word S if and only if the Levenshtein (Damerau-Levenshtein) distance between the words W and Sdoes not exceed the predetermined value N .
The Levenshtein state machine for the word W and the admissible number of modifications N can be defined as an ordered five elements A N (W) =
E is the alphabet of the automaton;
Q is the set of internal states;
q 0 - initial state, belongs to the set Q;
F is the set of final or final states;
V is a transition function that determines which state (s) can transition from the current state when the next symbol arrives at the input of the automaton.
The states of the nondeterministic Levenshtein automaton A N (W) are usually denoted as i #e , where i = 0 .. | W | , e = 0..N . If the machine is in state i #e , this indicates that the machine is enteredi “correct” characters and e modifications were detected . Since we consider an automaton that supports transpositions (that is , the Damerau-Levenshtein distance is used as p (S, W) ), the set of states must be supplemented by the states {i T #e } , where i = 0 .. | W | -1 , e = 1..N .
The initial state of the automaton is state 0 # 0 .
The set of final states includes states i #e for which the condition | W | - i <= N - e .
Based on the physical meaning of the states of the automaton, it is not difficult to determine the composition of admissible transitions. The transition function of the Levenshtein automaton is specified in the form of a table.
If you are interested in a rigorous mathematical justification of the composition of states of an automaton and the other theses stated above, you can find it in an article by Schultz and Mikhov (2002) .
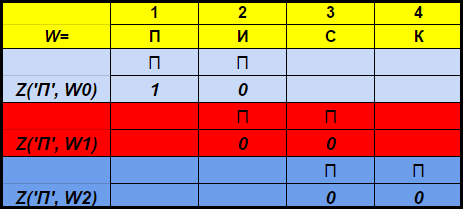
The characteristic vector Z (x, W i ) for the symbol x is the bit vector of length min (N + 1, | W | - i) , the kth element of which is 1 if the (i + k) th character of the string W is x , and 0 otherwise. For example, forW = ”LIST”
Z ('П', W 0 ) = <1, 0>, and Z ('П', W 1 ) = <0, 0>.
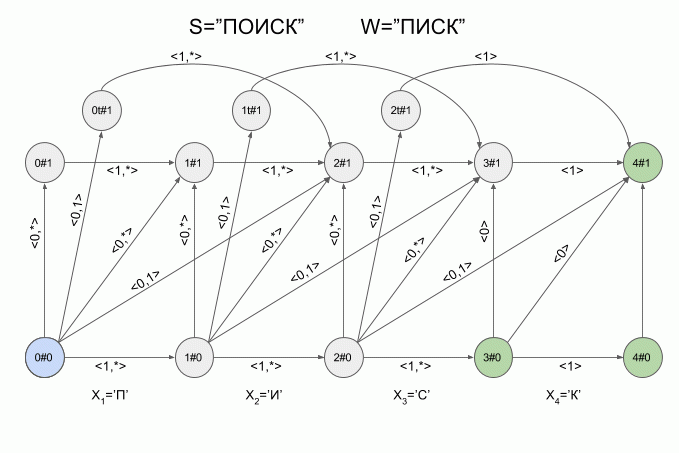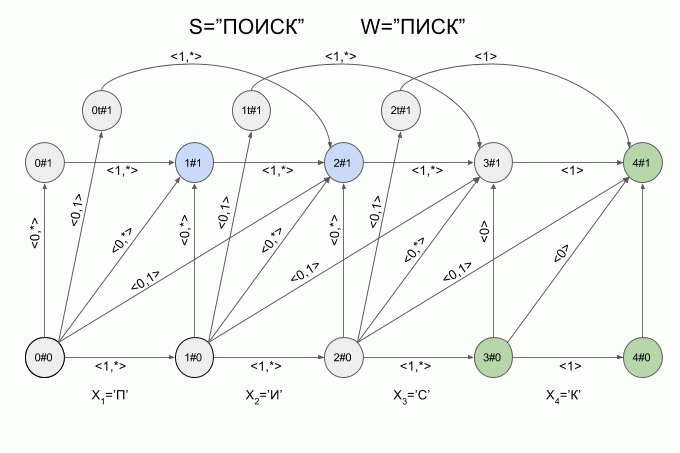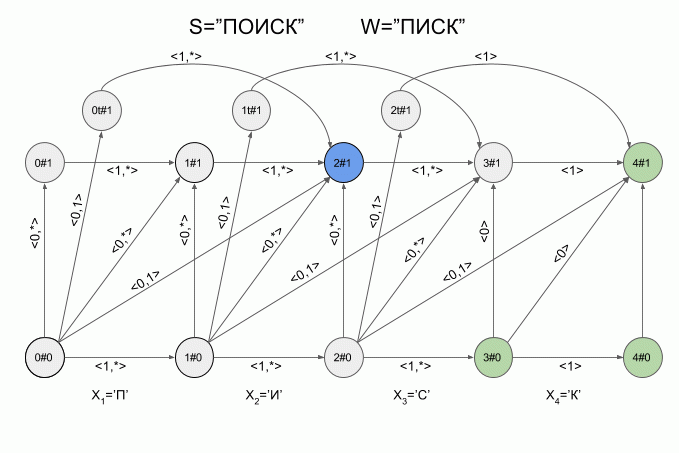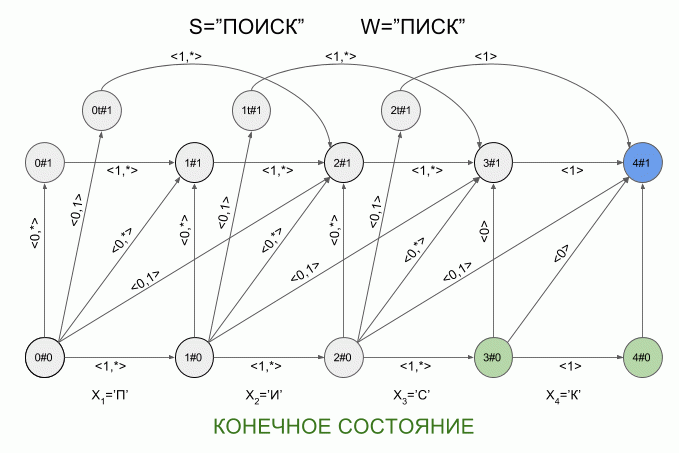
A graphical representation of the Levenshtein automaton for W = “LIST” and N = 1 is shown in the figure. The transitions of the automaton are signed by the corresponding characteristic vectors.

The final state of the automaton is highlighted in green. Light blue - the current (active) state of the machine.
The transition along the horizontal arrows is carried out when the “correct” symbol is entered into the machine.
The transition along the vertical arrows corresponds to the assumption that the next character entered into the machine is inserted into the original word W before (i + 1)th symbol. When moving along the vertical arrows, the machine “detects” a modification of the word W - the value of e increases by 1 .
The transition from state i #e to state (i + 1) # e + 1 corresponds to the assumption that the next character replaces (i +1) -th character in the word W .
The transition from state i #e to state (i + 2) # e + 1 corresponds to the assumption that the next character corresponds to the (i + 2) th character in the word W , and the (i + 1) th character of the wordW omitted in word S .
You probably already guessed that the transition to the state i T #e suggests that a transposition of the (i + 1) th and (i + 2) th characters of the word W has been detected .
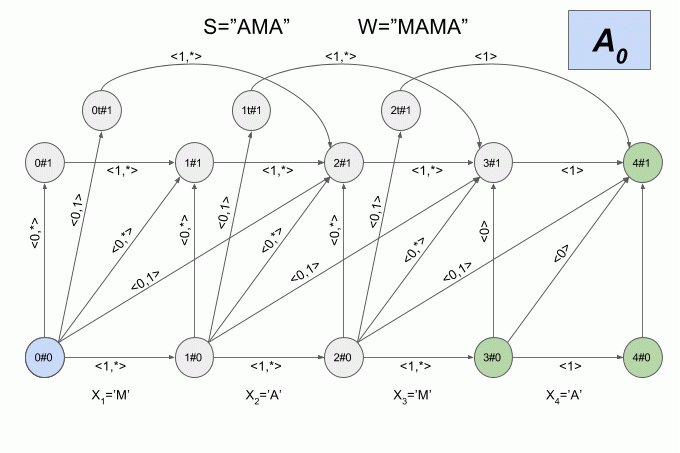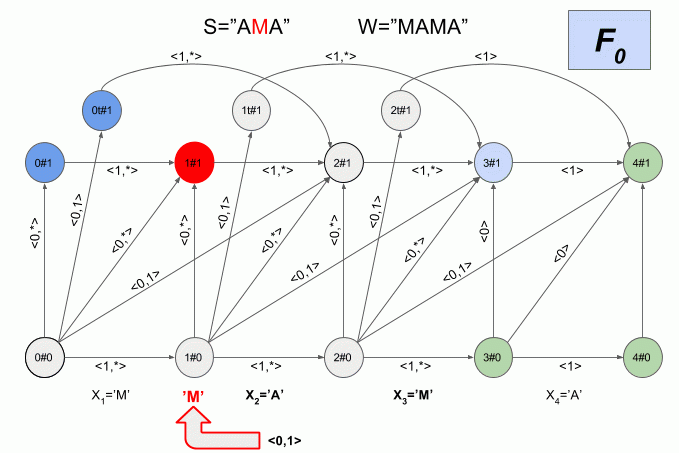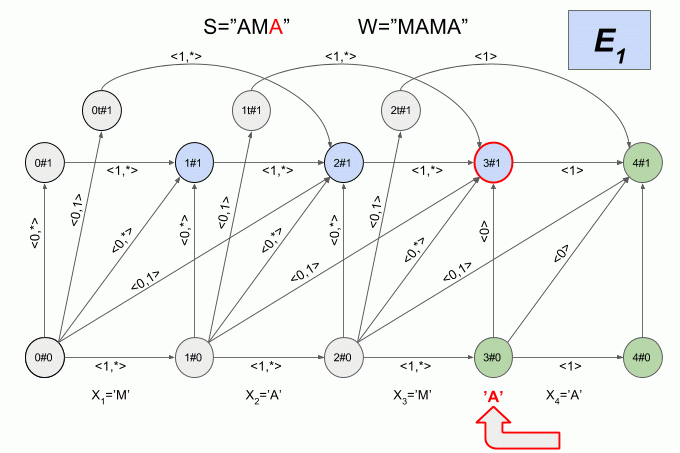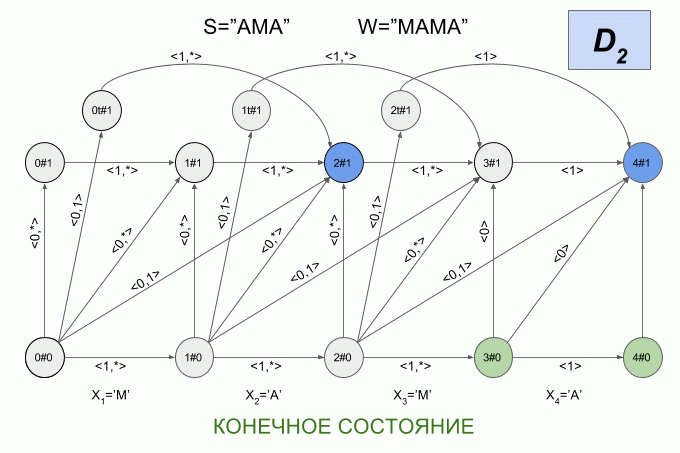
Now let's see how it works. I will indicate the entry of a new symbol into the machine by a curved red arrow, and to the right of the arrow indicate the value of the characteristic vector. This is how the machine A 1 (“LIST”) will work when you enter the word “SEARCH” into it.
Please note that in fact, the sequence of changes in the state of the automaton is determined not by a specific word supplied to the input of the automaton, but only by a sequence of characteristic vectors. This sequence may be the same for two different words. For example, if the automaton is set to the word “mother”, then the sequence of characteristic vectors will be the same for the words “lama”, “frame”, “lady”, etc.
Another interesting fact is that the structure of admissible transitions of the automaton does not change for i = 0 .. | W | - (N + 1) .
These two circumstances make it possible with the software implementation of fuzzy search algorithms to use an automaton that is not calculated for each specific word, but its universal imitation. That is why the title of the post refers to the “universal” Levenshtein automaton.
Automatic calculation for a specific word S is reduced in this case to a simple calculation of the characteristic vectors for each character x words S . The change of states is implemented in software as a simple increase in two variables e , i by a value determined from universal tables. Schulz and Mihov (2002) showed that the calculation of all characteristic vectors for the word Scan be produced in time O (| S |) . This is the temporary complexity of the machine.
The characters of the word S are sequentially fed to the input of the machine. If after supplying a certain character it becomes clear that the distance between the lines S and W exceeds the threshold value N , then the automaton is in the “empty” state - there are no active states in the automaton. In this case, the need to calculate the characteristic vectors for the remaining characters of the word S disappears.
This is how the machine “fulfills” the word S = ”ICS” with W = “LIST”:
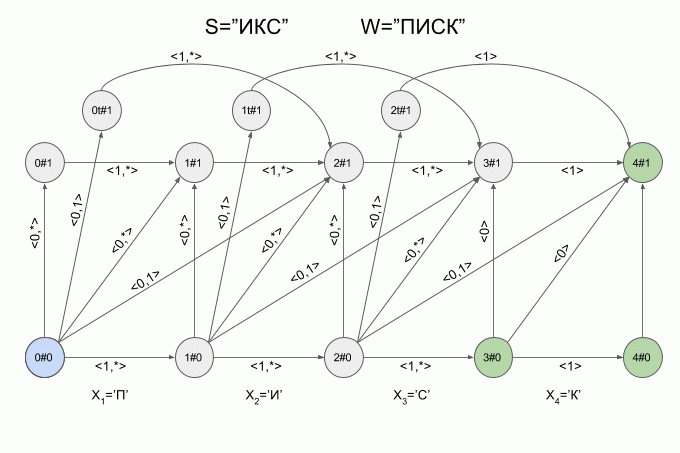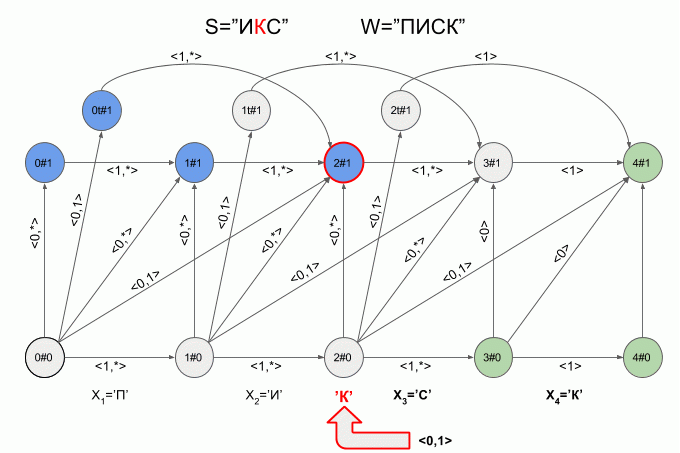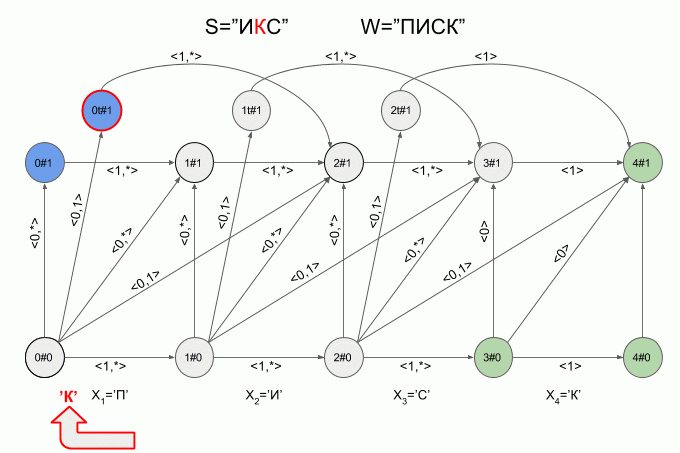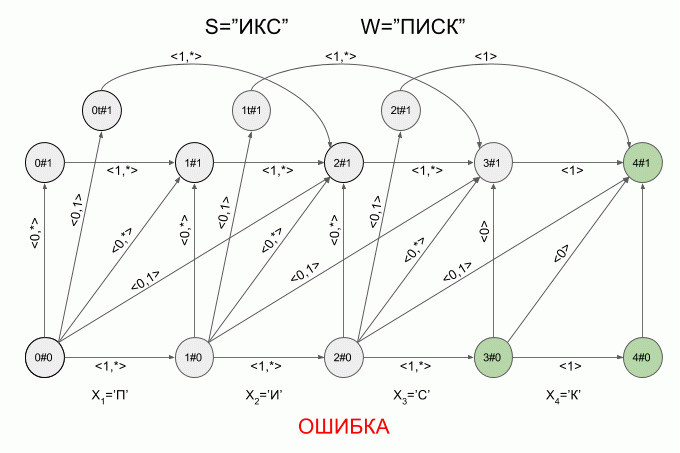
After entering the “I” symbol, four active states appeared immediately in the machine, however, after entering the “K” symbol, there were no active states - the machine was in an error state and did not accept the word “X”. In this case, the calculation of characteristic vectors for the symbol “C” was not carried out.
Deterministic Levenshtein automaton
In accordance with the determinization theorem, for any non-deterministic finite state machine, an equivalent deterministic finite state machine can be constructed. Why do we need a deterministic automaton? Just with a software implementation, it will work faster. Mainly due to the fact that it can have only one current state and, as a result, when entering the next character, it will be necessary to calculate only one characteristic vector and determine only one transition from the transition table.
If for the nondeterministic Levenshtein automaton A 1 (W) considered abovesorting through all possible values of the characteristic vectors, we can make sure that the states that make up one of the following sets can be simultaneously active: The
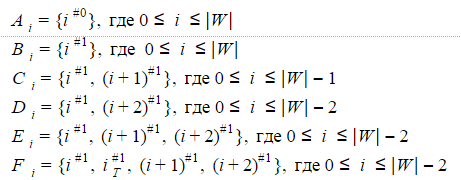
six sets listed above will be the states of the determinate Levenshtein automaton for N = 1. More precisely, the automaton will have six states for i = 0 .. | W | -2 , three states for i = | W | -1, and two more states for i = | W | .
The dimension of the characteristic vector for a deterministic automaton can be calculated as 2N + 1 . Then the transition table of the automaton for a word from | W | letters with N = 1 should have 2 2x1 + 1rows and 6x (| W | -1) + 3 + 2 columns (for example, 8x35 for a word of 6 letters). In addition, such a table will have to be calculated for each value of | W | separately. This is not very convenient and requires additional time for calculation or additional memory for storage.
However, as I wrote above, the composition of admissible transitions of the automaton does not change for i = 0 .. | W | - (2N + 1) . Therefore, in software implementation it is much more convenient to simulate a deterministic automaton instead of calculating the real one. To do this, it is enough to store the offset value i and use the universal transition table with eight rows and six columns. Such a table can be calculated in advance.
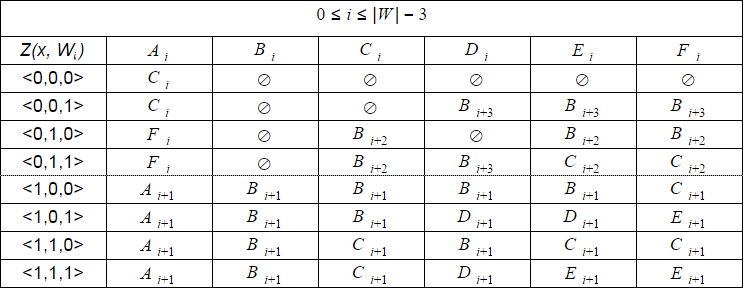
As i increasessome states of the automaton become unattainable; therefore, for i = | W | -2 .. | W | Separate smaller tables should be provided.
Further, speaking of the deterministic Levenshtein automaton, I will mean precisely the above-described universal imitation.
With increasing N, the number of states increases exponentially. So, for N = 2, the deterministic automaton can have 42 states, for N = 3, several hundred already. And that means that memory consumption will be proportional to O (N 2 ) .
The initial state of the deterministic Levenshtein automaton will be the state A 0 .
What conditions will be final? Those that correspond to the final states of a non-deterministic automaton. For N = 1, these will be the states A | W | , B | W | , A | W | -1 , C | W | -1 , D | W | -2 , E | W | -2 , F | W | -2 .
Since the number of transitions between the six states is very large, and the physical meaning of the states of the determined Levenshtein automaton is not obvious, I will not give here a graphical representation of it. I think that the picture is not quite clear. If you still want to see her, you can find in the articleMihov and Schulz (2004) . I will give one more example of the operation of a non-deterministic automaton, but this time I will indicate in what state its deterministic equivalent is at every moment.
Software implementation of the determined Levenshtein automaton
I wrote the software implementation of the Levenshtein automaton in C # - I am most familiar with this language. You can find the source here . Universal conversion tables are implemented as fields of the static class ParametricDescription. The class contains universal conversion tables for N = 1,2.
In addition to conversion tables, the ParametricDescription class also contains offset increment tables. The offset increment is the value by which you need to increase the value of i when moving to the next state.
The Levenshtein automaton itself is implemented in the LevTAutomataImitation class. All class methods are very simple and I will not describe them in detail. When performing a fuzzy search in the dictionary, it is enough to create one instance of the class per request.
Please note - the creation of an instance LevTAutomataImitation performed in a short time constant for all values of the W , the S , of N . Only a W value and auxiliary variables of small size are stored in an instance of the class .
To select from the array of strings only those strings that are no more than 2 distant from the given Damerau-Levenshtein distance, you can use the following code:
//Misspelled word
string wordToSearch = "fulzy";
//Your dictionary
string[] dictionaryAsArray = new string[] { "fuzzy", "fully", "funny", "fast"};
//Maximum Damerau-Levenstein distance
const int editDistance = 2;
//Constructing automaton
LevTAutomataImitation automaton = new LevTAutomataImitation (wordToSearch, editDistance);
//List of possible corrections
IEnumerable corrections = dictionaryAsArray.Where(str => automaton.AcceptWord(str));
The given code implements the simplest fuzzy search algorithm in the dictionary using the Levenshtein automaton - the algorithm of exhaustive search. Of course, this is not the most efficient algorithm. I will discuss more efficient search algorithms using the Levenshtein automaton in the second part of the article .
References
- Sources for an article in C #
- distance Lowenstein
- Distance Damerau-Levenshtein
- State machine
- Good post about fuzzy search in dictionary and text
- Brief description of the Levenshtein automaton
- A detailed mathematical description of the Levenshtein automaton in an article by Schultz and Mihov (2002)
- Another article by Mikhov and Schulz (2004) on the same topic
- The history of the implementation of the Levenshtein automaton in the fuzzy search Lucene
- Implementations in java: one and two
- The second part of my publication
