Again about the Voronoi diagrams
- Transfer
As written in recent blog posts , I struggled to get the necessary detail of coastlines in my game Dragons Abound . My disappointment arose during the implementation of the barrier islands . To create the island as narrow as possible, I made them one location wide — in the figure below each location is a Delone triangle:
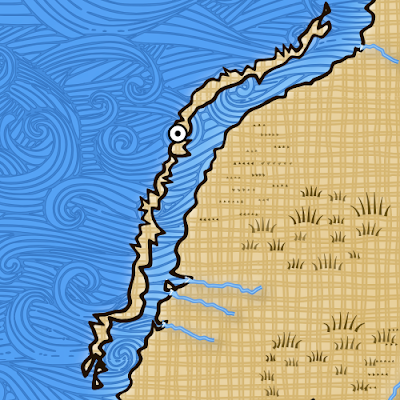
It was rather unpleasant - and because the island was very broken, and because the size of the parts was too large. It seemed that with a strong increase in the number of Delone triangles (that is, with a strong decrease in their size), this problem would be solved - but the density of triangles I needed caused the browser to crash.
I solved this problem by separating the land contours from the internal view of the locations. This allowed me to draw islands of any size or shape, regardless of the underlying grid of locations:
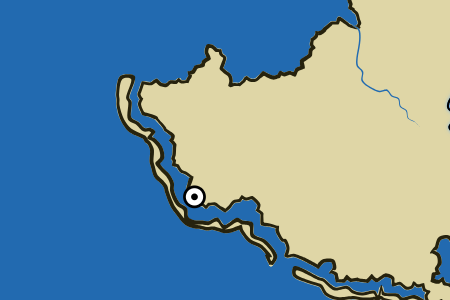
So, the problem is solved! This allowed me to draw the barrier islands, and since the coastline is no longer required to follow the basic grid, if necessary, a more detailed coastline could be created in the usual way, and then added details.
But ... how do we add details to the shoreline? This is not as easy as you might think. Since I wanted to create a fractal coastline, I considered the possibility of using fractals that add details to the coastline:

Having experimented with the settings, I was able to add a lot of details and interesting things to the coastline. However, the system could not create something resembling such a map:
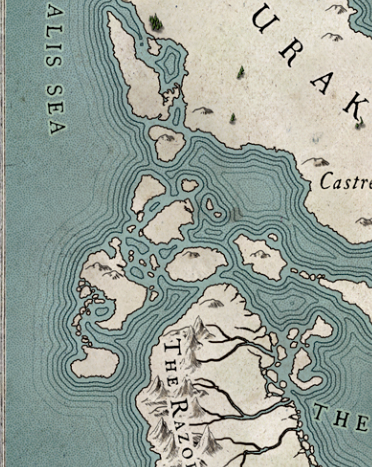
Perlin's noise can create a similar type of relief with a sufficiently detailed base grid, but can this be done without storing the elevation values in the base grid with the desired resolution (I know that it will break my code)? Until I figured out how to do it. The coastline is essentially a path through all points where the Perlin noise function has zero value. Although we can learn directly from the Perlin noise function the value in a specific location (X, Y), it is impossible to find (suppose) “all locations in which the function has zero value”. That is, it is difficult to see how to draw a contour of heights without a base grid.
Worse, I asked Amithow to do it, and he also did not know the answer. It's one thing when I can’t say this, but when even such an intelligent person cannot give an answer, I start thinking that this cannot be done. Sadly I can give the shoreline any shape I need, but I cannot get the shapes I need without a very detailed base grid.
So how can I get a high-resolution grid without breaking the code?
One of the solutions that came to my mind resembles what Azgaar madein his generator of maps - Voronoi cells of variable size. The basic idea is to increase the density (and decrease in size) of the base grid along coastlines and to maintain a lower density in oceans and other areas that do not require detail. With this option, I will have a lot of mesh cells only in those areas where you need detail. This change will be quite difficult to implement in Dragons Abound , but I want to think about it. On the other hand, Azgaar himself was not very pleased with this approach , so this should also be taken into account.
In parallel, I wanted to investigate the causes of browser failure when processing a heap of triangles. Chrome developer tools provided me with detailed performance information. I am by no means an expert in using these tools, but many features are simple enough that anyone can understand them. In case you want to know the total amount of memory used in the program, in the Memory tab there is information about the current used volume:
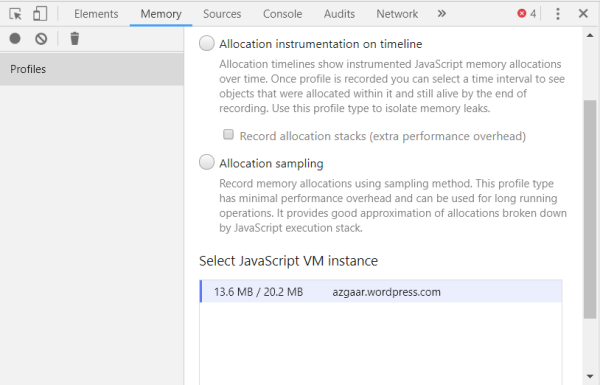
In this case, I opened the Azgaar webpage, and it takes up a modest 20 MB of memory. You can use this tool to find out how much memory the Dragons Abound takes , and determine the point at which the tab fails.
The basic parameter that controls the resolution of the underlying grid in Dragons Abound is cleverly named "npts" (Number of Points). For each unit map area (maps of regions, which I usually use as examples, have an area of 1 unit) Dragons Abound creates a given number of base grid locations. I usually use npts for 16K (16384), and this means that each grid location corresponds to approximately 70 square pixels of the screen at a standard zoom scale.

Of course, the exact amount of memory used depends on the card, but for the 16K-dot card shown above, you need approximately 92 MB:
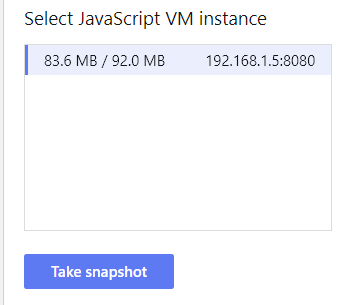
This is less than I expected, and, frankly, a rather modest figure.
If you double the number of points in the base grid, the memory will increase to 138 MB:
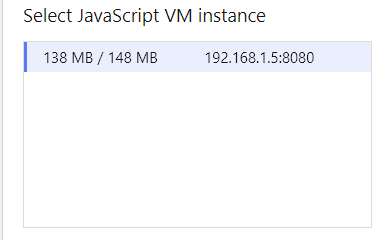
The size of the occupied memory has not doubled, because part of this memory is occupied by resources and other data structures, the size of which has not changed. 16K additional points "weigh" about 50 MB of memory, that is, each point in the result takes about 3 KB of memory. This is more than I expected, but in general the volume is still quite modest. On a computer with 64 GB of memory, 150 MB is barely noticeable.
Having completed a few more doublings, I found that the tab with Dragons Abound usually crashes at about 128K points. If you catch her before she flies out and check her memory, we will see the following:
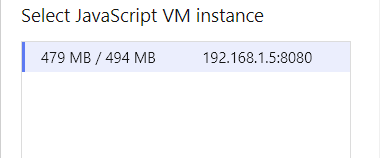
I assumed that the tab fails due to memory usage, but usually the problem is not in memory. Why does the tab crash? The only clue is that the tab does not crash until the map is completed, and this is probably an indication that a crash occurs during rendering.
It is logical to assume that the SVG I create overloads the browser renderer, due to its size or complexity. First, I can find out how many SVG elements I create. In D3, I can get the total number of SVG elements created using
Running from 16K points and checking the number of SVG elements showed me the following:

32K points have 65457 elements, and 128K points - 258823. Each point added to the base grid adds two elements to the map. I think I found the source of the trouble.
Each point of the base grid adds SVG elements due to the way Dragons Abound renders land (and water). The land is rendered by drawing each base location as a filled polygon and then blurring them all. This allows Dragons Abound to give the land a beautiful pattern or use the height of sushi to render sushi with 3D shading, as shown here:
You can turn off the land and ocean visualization to check how many SVG elements are created. At 256K points:

Wow, the number of SVG elements has dropped significantly. As I hoped, now the map is rendered without a glitch! That is, if you avoid using the grid for rendering sushi and water, you can create a much more dense grid than before.
Now that I have a much more dense Voronoi grid, I want to check whether it allows me to generate the necessary land elements of the land, such as coastal islands. The dense Voronoi grid creates other problems (especially with rivers), so I will disconnect everything except the coastlines in order to speed up the testing and focus on them. Here is the original render of a certain coastline with 256K points and with standard noise:
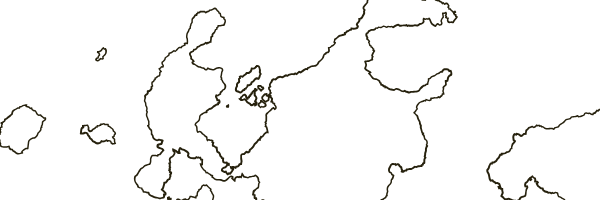
It turns out that the map is rendered well, and already creates a much more beautiful coastline.
Even without careful adjustment, the result was much better. Noise creates the types of fractal coastlines and coastal islands that I have indicated on the map above.
Here are the islands with an increase of 300%:
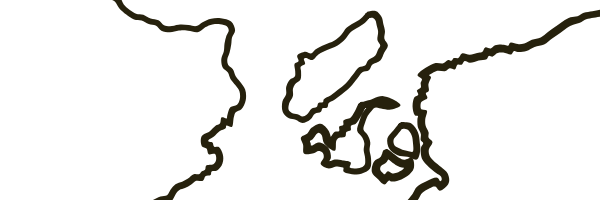
With such an increase, you can see the artifacts of triangles from the base grid, but even so, islands can create interesting shapes. You can use anti-aliasing (as I do on the current map version) to get rid of some of the most noticeable triangle artifacts. At standard magnification, this provides a less rugged coastline, but also eliminates some small details:
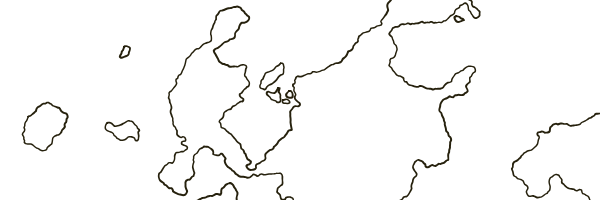
Probably have to do the adjustment to get the middle ground.
Most procedural sushi generators use Perlin noise to create a height map. It is necessary to find suitable noise parameters, select a seed, and then use the noise value in each location (x, y) to set the land mass. One of the convenient aspects of sushi creation is that if you need more details on the coastline, you can simply adjust the noise parameters.
However, Dragons Abound does not create land in this way. (Or at least, creates not only such.) In Dragons AboundThere are many different ways to create sushi. Although they all use noise to varying degrees, very few of them create land directly from noise. For example, the game has a procedure for creating an island that creates a mask for the island (usually an ellipse), uses noise to give the ellipse a more natural shape, and then applies various noise to roughly fill the mask. Each specific card is usually created by a combination of several different procedures. Therefore, adding details by setting the noise parameters for Dragons Abound is not very suitable.
For my purposes, it is better to approach the problem from a slightly different angle. If I have a definite height map defining the masses of land, how can I add details to the edges of these land masses? This may lead us to think that we need to recognize the edges of the masses of land and mask the rest of the map, etc. But, on the other hand, I do not mind adding additional details to the rest of the map. If the land is a little more uneven or the ocean floor is a bit more rough, then this is normal.
What does adding parts to the shoreline mean? A coastline is simply a contour line in which the elevation map is zero. (The value is arbitrary, but this principle is used in each procedural sushi generator.) To make this line more detailed, you need to slightly shift the land next to this contour lines up and down a bit to make simple coastlines more difficult, parts of land to come out into the ocean and islands, and so on. But this should not happen quite by accident, I want the changes to appear natural. We summarize all this, and it begins to seem like you need to add a small amount of noise to the entire map. And in fact, that is what I did in the original example shown above.
Of course, this must be done carefully so as not to erase the masses of land created and not create other problems. Essentially, I need to configure three parameters.
The first is the scale of the noise. Scale is just a range of values for this noise. In our case, I want to lower some areas down, and raise some upwards, so the range of values should be from negative to positive. However, I do not want to add new mountains or create an ocean far from the existing coastline, so I will make the maximum (absolute) noise value a small fraction of the standard land height.
The second parameter is the main noise frequency. Frequency determines how quickly the noise changes within the location. Low-frequency noise changes very slowly, so a positive region with low-frequency noise can (suppose) cover the entire map. High-frequency noise changes rapidly, so a positive region with high-frequency noise can (say) have the size of a small island. In our case, the main frequency of the noise determines the largest elements of the relief, which we will see in the noise. That is, if I want the noise to be able to add (say) small islands to the map (but nothing larger than them), then I need to choose a main frequency the size of a small island.
You might think that this is easy to do (just measure a small island and assign this size to the main frequency). However, the frequency is measured in the coordinates of the noise function, and not the coordinates of the map! A typical noise function can have an interval from 0 to 255 at each coordinate, and a map can have an interval from -1 to 1 at each coordinate. Worse is that the noise coordinates are collapsed, and many noise users do not even realize this. Converting from one unit to another and identifying suitable frequencies is confusing, so it is usually easiest to simply experiment with frequency intervals and choose the one that creates the map elements of the desired size.
The third parameter is the number of octaves of noise. Octaves are additional layers of noise. Each layer usually doubles the frequency and halves the noise scale. That is, each new layer adds relief elements two times smaller than the previous layer, but also two times weaker. That is, you need to choose the number of octaves, giving the smallest elements we need, and for this you may need to adjust the scale of the noise, because it is still strong enough in the highest octave to appear on the map. Since I deliberately do this to make the coastlines very intricate, I will use quite a few octaves of noise.
Let's get down to setting it up. First, I will generate an example map without additional noise:

Obviously, this is a boring coastline, with smooth lines and just a couple of large islands. Here is the same coastline with the original noise sample:
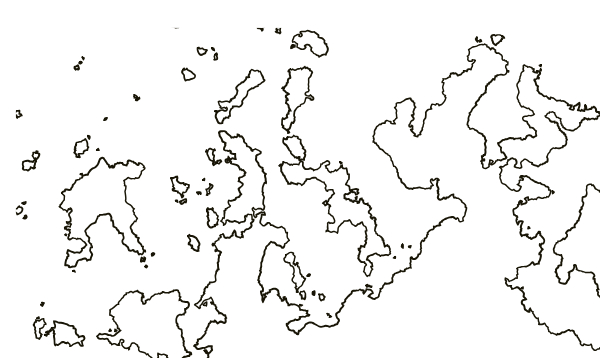
Noise has significantly changed the shape of the map, turning large pieces of land into the ocean, and vice versa. There are also many islands, including far into the sea. All this indicates that the scale of the noise is too large. The largest individual terrain elements added by noise should be the size of small islands of the original map. This is probably the maximum new size of the elements, proving that the basic frequency of the noise is roughly chosen correctly. Finally, many small details appeared, up to the limits of the display size, and this shows that there are enough octaves. (However, the number of octaves may be more than necessary. This does not affect the appearance of the map, but is inefficient.) It seems that basically you need to adjust the noise scale.
Tuning noise is a rather complicated operation, because I want this noise to mainly affect land and water at about a contour line with height = 0. That is, I need a relatively small scale, but it is not clear how to choose the correct number, because in different maps the distribution of heights varies. The solution is to select a suitable scale on the fly. You can take all the absolute values of the heights on the map, sort them, and find the cut-off point that selects (let's say) 10% of the locations around zero. All these locations fall into the interval (suppose) [-0.05, 0.05], and then I can use the value 0.05 to determine the scale of the added noise.
(I am writing “definitions” because for various reasons you cannot just use 0.05. First you need to turn land into water and vice versa. Adding (let's say) 0.002 to -0.05 will not make any visible changes to the map. That is, the interval should be much more than 0.05 , if I want to convert a significant proportion of locations with a height of -0.05 from water to land, and secondly, the noise functions are not evenly distributed , therefore, with a scale of 0.05, the noise function will never actually return a value of 0.05! In practice, the difficulty is that the scale should be much bigger than the greatest values that we want to see often enough.)
Having experimented, I found a value that adds complexity to the coastlines, without changing them significantly, and also creating a small number of islands:
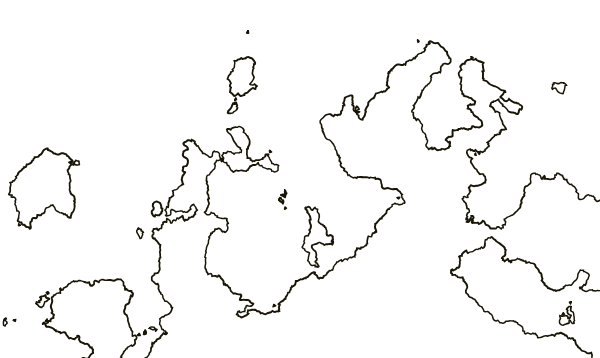
As always, these parameters in the game can take a range of values, so I can get a wide range of maps: from maps with fairly smooth coasts to maps with broken and difficult shores. By allowing the program to pick values, I got the following result:
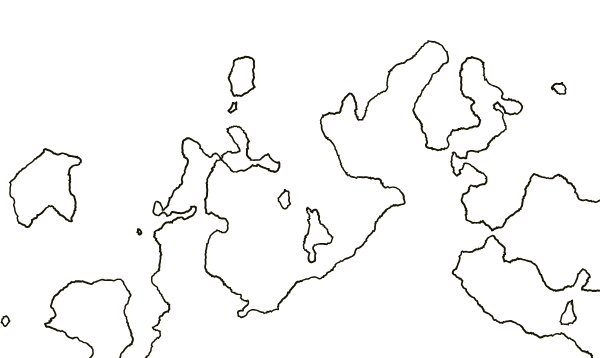
The coastlines are on a smoother side, but there is still a large part of the added complexity of medium scale and a sufficient number of new islands.
When implementing fractal coastlines, I realized the ability to control the level of fractalization using the noise function, so some areas will have smooth coasts and others complex. I thought that this would greatly increase the interestingness of the map, and it would look less “generated”, so I’ll add this feature here. The idea is quite simple - before adding coastline noise to the map, I multiply it by the output of the second noise function, which varies from zero to 1. Where this function is small, small details will be added to the coastlines. Where it is close to 1, additional details will be added completely. Selecting the scale of the second noise function, which slowly varies throughout the map, I will get some areas with complex coastlines, a part with simple ones, and logical transitions between them:
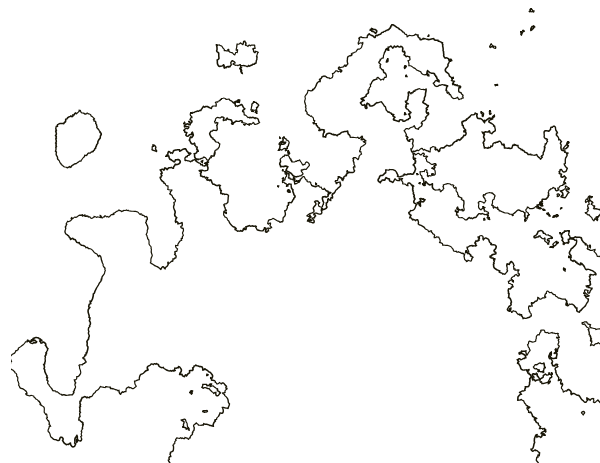
Here I made the coastal parameters with large values so that the difference would be clearer. We see a wild, indented coast in the northeast, and smoother beaches in the west.
So, we have significantly improved the coastline generation, but I still cannot completely generate a map with so many Delone triangles. I only show the contour maps, because many other map elements are broken. Need to fix it.
The rest of the program does not work well with so many Delone triangles (at current settings of 256K). The main problem is that Dragons Abounddraws land and water by drawing all the individual triangles, and this number of SVG elements causes the browser to crash. So I had to completely turn off sushi rendering. There is probably a way around this problem, but having so many triangles creates other problems. For example, some parts of the program must process the entire map. Each of them becomes at 256K locations sixteen times slower than at 16K locations. There are also parts in the code (for example, a new precipitation model) that break when working with so many triangles. And we don’t gain anything by creating such a detailed grid of locations - after generating the coastline, nothing gets better from the added complexity. So even though I could look at the program and fix those areas
As mentioned above, Azgaar has already done work on changing the resolution of the Voronoi grid underlying the map. He realized the possibility of changing the grid resolution on the fly during the generation process, that is, he could (for example) increase the density of locations along the coast. However, the local density change has its drawbacks - in particular, it creates triangles of a strange shape along the border. Later, Azgaar expressed the opinion that the system is too complex and not worth the effort. Azgaar usually knows what he is talking about, so I will take his word for it, and I will not try to repackage the finished grid.
Instead, I created a second grid with the desired (lower) resolution, and then copied the elevation map to this new grid. (Do not forget that Dragons Aboundnow keeps shorelines separate from the grid, so after they are created, they no longer depend on the exact matching grid. Make it a bit complicated. Since the original grid has a much higher resolution than the new one, many locations in the original grid will be superimposed on one location in the new grid. Each of these source locations has a different height on the height map, how can I copy them? Use the mean? Or the maximum (minimum) height?
For starters, I will simply select one random location to simply see if the new grid will work with the rest of the program:
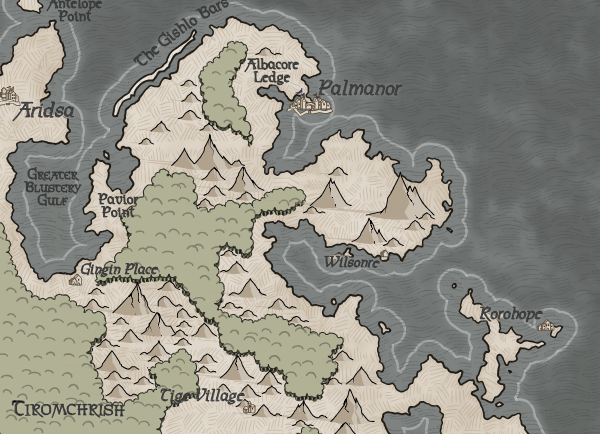
Everything turned out surprisingly good. A minor bug occurs when new locations are not properly labeled as land, beach or water, but after solving this problem, the card generation worked fine. It is necessary to clean up minor issues (for example, the label Palmanor, which came to water), but on the whole everything looks good. Even the tiny islands turned out beautiful.
In the end, I decided that by reducing the resolution of the Voronoi grid, each location would be the average of the base locations. This seems like a sensible decision, and if necessary it can always be changed. This image shows how, as a result, coastlines are separated from the finished grid:

To summarize: Dragons Abound uses a very high resolution Delone triangle grid to generate a height map. After it is completed, Dragons Abound identifies coastlines, tracking transitions from negative to positive values in the elevation map. Then the game copies the high-resolution grid into a much smaller grid, averaging locations that fall into one location of the new grid. Next, the high resolution grid is discarded, and the rest of the procedural generation and visualization continues on the low resolution grid. An interesting question is whether the use of the Delaunay mesh is of any value at this stage; it may be worth simply copying to a grid of hexagons or something similar.

It was rather unpleasant - and because the island was very broken, and because the size of the parts was too large. It seemed that with a strong increase in the number of Delone triangles (that is, with a strong decrease in their size), this problem would be solved - but the density of triangles I needed caused the browser to crash.
I solved this problem by separating the land contours from the internal view of the locations. This allowed me to draw islands of any size or shape, regardless of the underlying grid of locations:

So, the problem is solved! This allowed me to draw the barrier islands, and since the coastline is no longer required to follow the basic grid, if necessary, a more detailed coastline could be created in the usual way, and then added details.
But ... how do we add details to the shoreline? This is not as easy as you might think. Since I wanted to create a fractal coastline, I considered the possibility of using fractals that add details to the coastline:

Having experimented with the settings, I was able to add a lot of details and interesting things to the coastline. However, the system could not create something resembling such a map:

Perlin's noise can create a similar type of relief with a sufficiently detailed base grid, but can this be done without storing the elevation values in the base grid with the desired resolution (I know that it will break my code)? Until I figured out how to do it. The coastline is essentially a path through all points where the Perlin noise function has zero value. Although we can learn directly from the Perlin noise function the value in a specific location (X, Y), it is impossible to find (suppose) “all locations in which the function has zero value”. That is, it is difficult to see how to draw a contour of heights without a base grid.
Worse, I asked Amithow to do it, and he also did not know the answer. It's one thing when I can’t say this, but when even such an intelligent person cannot give an answer, I start thinking that this cannot be done. Sadly I can give the shoreline any shape I need, but I cannot get the shapes I need without a very detailed base grid.
So how can I get a high-resolution grid without breaking the code?
One of the solutions that came to my mind resembles what Azgaar madein his generator of maps - Voronoi cells of variable size. The basic idea is to increase the density (and decrease in size) of the base grid along coastlines and to maintain a lower density in oceans and other areas that do not require detail. With this option, I will have a lot of mesh cells only in those areas where you need detail. This change will be quite difficult to implement in Dragons Abound , but I want to think about it. On the other hand, Azgaar himself was not very pleased with this approach , so this should also be taken into account.
In parallel, I wanted to investigate the causes of browser failure when processing a heap of triangles. Chrome developer tools provided me with detailed performance information. I am by no means an expert in using these tools, but many features are simple enough that anyone can understand them. In case you want to know the total amount of memory used in the program, in the Memory tab there is information about the current used volume:

In this case, I opened the Azgaar webpage, and it takes up a modest 20 MB of memory. You can use this tool to find out how much memory the Dragons Abound takes , and determine the point at which the tab fails.
The basic parameter that controls the resolution of the underlying grid in Dragons Abound is cleverly named "npts" (Number of Points). For each unit map area (maps of regions, which I usually use as examples, have an area of 1 unit) Dragons Abound creates a given number of base grid locations. I usually use npts for 16K (16384), and this means that each grid location corresponds to approximately 70 square pixels of the screen at a standard zoom scale.

Of course, the exact amount of memory used depends on the card, but for the 16K-dot card shown above, you need approximately 92 MB:

This is less than I expected, and, frankly, a rather modest figure.
If you double the number of points in the base grid, the memory will increase to 138 MB:

The size of the occupied memory has not doubled, because part of this memory is occupied by resources and other data structures, the size of which has not changed. 16K additional points "weigh" about 50 MB of memory, that is, each point in the result takes about 3 KB of memory. This is more than I expected, but in general the volume is still quite modest. On a computer with 64 GB of memory, 150 MB is barely noticeable.
Having completed a few more doublings, I found that the tab with Dragons Abound usually crashes at about 128K points. If you catch her before she flies out and check her memory, we will see the following:

I assumed that the tab fails due to memory usage, but usually the problem is not in memory. Why does the tab crash? The only clue is that the tab does not crash until the map is completed, and this is probably an indication that a crash occurs during rendering.
It is logical to assume that the SVG I create overloads the browser renderer, due to its size or complexity. First, I can find out how many SVG elements I create. In D3, I can get the total number of SVG elements created using
svg.selectAll('*').size(). Running from 16K points and checking the number of SVG elements showed me the following:

32K points have 65457 elements, and 128K points - 258823. Each point added to the base grid adds two elements to the map. I think I found the source of the trouble.
Each point of the base grid adds SVG elements due to the way Dragons Abound renders land (and water). The land is rendered by drawing each base location as a filled polygon and then blurring them all. This allows Dragons Abound to give the land a beautiful pattern or use the height of sushi to render sushi with 3D shading, as shown here:

You can turn off the land and ocean visualization to check how many SVG elements are created. At 256K points:

Wow, the number of SVG elements has dropped significantly. As I hoped, now the map is rendered without a glitch! That is, if you avoid using the grid for rendering sushi and water, you can create a much more dense grid than before.
Now that I have a much more dense Voronoi grid, I want to check whether it allows me to generate the necessary land elements of the land, such as coastal islands. The dense Voronoi grid creates other problems (especially with rivers), so I will disconnect everything except the coastlines in order to speed up the testing and focus on them. Here is the original render of a certain coastline with 256K points and with standard noise:

It turns out that the map is rendered well, and already creates a much more beautiful coastline.
Even without careful adjustment, the result was much better. Noise creates the types of fractal coastlines and coastal islands that I have indicated on the map above.
Here are the islands with an increase of 300%:

With such an increase, you can see the artifacts of triangles from the base grid, but even so, islands can create interesting shapes. You can use anti-aliasing (as I do on the current map version) to get rid of some of the most noticeable triangle artifacts. At standard magnification, this provides a less rugged coastline, but also eliminates some small details:

Probably have to do the adjustment to get the middle ground.
Most procedural sushi generators use Perlin noise to create a height map. It is necessary to find suitable noise parameters, select a seed, and then use the noise value in each location (x, y) to set the land mass. One of the convenient aspects of sushi creation is that if you need more details on the coastline, you can simply adjust the noise parameters.
However, Dragons Abound does not create land in this way. (Or at least, creates not only such.) In Dragons AboundThere are many different ways to create sushi. Although they all use noise to varying degrees, very few of them create land directly from noise. For example, the game has a procedure for creating an island that creates a mask for the island (usually an ellipse), uses noise to give the ellipse a more natural shape, and then applies various noise to roughly fill the mask. Each specific card is usually created by a combination of several different procedures. Therefore, adding details by setting the noise parameters for Dragons Abound is not very suitable.
For my purposes, it is better to approach the problem from a slightly different angle. If I have a definite height map defining the masses of land, how can I add details to the edges of these land masses? This may lead us to think that we need to recognize the edges of the masses of land and mask the rest of the map, etc. But, on the other hand, I do not mind adding additional details to the rest of the map. If the land is a little more uneven or the ocean floor is a bit more rough, then this is normal.
What does adding parts to the shoreline mean? A coastline is simply a contour line in which the elevation map is zero. (The value is arbitrary, but this principle is used in each procedural sushi generator.) To make this line more detailed, you need to slightly shift the land next to this contour lines up and down a bit to make simple coastlines more difficult, parts of land to come out into the ocean and islands, and so on. But this should not happen quite by accident, I want the changes to appear natural. We summarize all this, and it begins to seem like you need to add a small amount of noise to the entire map. And in fact, that is what I did in the original example shown above.
Of course, this must be done carefully so as not to erase the masses of land created and not create other problems. Essentially, I need to configure three parameters.
The first is the scale of the noise. Scale is just a range of values for this noise. In our case, I want to lower some areas down, and raise some upwards, so the range of values should be from negative to positive. However, I do not want to add new mountains or create an ocean far from the existing coastline, so I will make the maximum (absolute) noise value a small fraction of the standard land height.
The second parameter is the main noise frequency. Frequency determines how quickly the noise changes within the location. Low-frequency noise changes very slowly, so a positive region with low-frequency noise can (suppose) cover the entire map. High-frequency noise changes rapidly, so a positive region with high-frequency noise can (say) have the size of a small island. In our case, the main frequency of the noise determines the largest elements of the relief, which we will see in the noise. That is, if I want the noise to be able to add (say) small islands to the map (but nothing larger than them), then I need to choose a main frequency the size of a small island.
You might think that this is easy to do (just measure a small island and assign this size to the main frequency). However, the frequency is measured in the coordinates of the noise function, and not the coordinates of the map! A typical noise function can have an interval from 0 to 255 at each coordinate, and a map can have an interval from -1 to 1 at each coordinate. Worse is that the noise coordinates are collapsed, and many noise users do not even realize this. Converting from one unit to another and identifying suitable frequencies is confusing, so it is usually easiest to simply experiment with frequency intervals and choose the one that creates the map elements of the desired size.
The third parameter is the number of octaves of noise. Octaves are additional layers of noise. Each layer usually doubles the frequency and halves the noise scale. That is, each new layer adds relief elements two times smaller than the previous layer, but also two times weaker. That is, you need to choose the number of octaves, giving the smallest elements we need, and for this you may need to adjust the scale of the noise, because it is still strong enough in the highest octave to appear on the map. Since I deliberately do this to make the coastlines very intricate, I will use quite a few octaves of noise.
Let's get down to setting it up. First, I will generate an example map without additional noise:

Obviously, this is a boring coastline, with smooth lines and just a couple of large islands. Here is the same coastline with the original noise sample:

Noise has significantly changed the shape of the map, turning large pieces of land into the ocean, and vice versa. There are also many islands, including far into the sea. All this indicates that the scale of the noise is too large. The largest individual terrain elements added by noise should be the size of small islands of the original map. This is probably the maximum new size of the elements, proving that the basic frequency of the noise is roughly chosen correctly. Finally, many small details appeared, up to the limits of the display size, and this shows that there are enough octaves. (However, the number of octaves may be more than necessary. This does not affect the appearance of the map, but is inefficient.) It seems that basically you need to adjust the noise scale.
Tuning noise is a rather complicated operation, because I want this noise to mainly affect land and water at about a contour line with height = 0. That is, I need a relatively small scale, but it is not clear how to choose the correct number, because in different maps the distribution of heights varies. The solution is to select a suitable scale on the fly. You can take all the absolute values of the heights on the map, sort them, and find the cut-off point that selects (let's say) 10% of the locations around zero. All these locations fall into the interval (suppose) [-0.05, 0.05], and then I can use the value 0.05 to determine the scale of the added noise.
(I am writing “definitions” because for various reasons you cannot just use 0.05. First you need to turn land into water and vice versa. Adding (let's say) 0.002 to -0.05 will not make any visible changes to the map. That is, the interval should be much more than 0.05 , if I want to convert a significant proportion of locations with a height of -0.05 from water to land, and secondly, the noise functions are not evenly distributed , therefore, with a scale of 0.05, the noise function will never actually return a value of 0.05! In practice, the difficulty is that the scale should be much bigger than the greatest values that we want to see often enough.)
Having experimented, I found a value that adds complexity to the coastlines, without changing them significantly, and also creating a small number of islands:

As always, these parameters in the game can take a range of values, so I can get a wide range of maps: from maps with fairly smooth coasts to maps with broken and difficult shores. By allowing the program to pick values, I got the following result:

The coastlines are on a smoother side, but there is still a large part of the added complexity of medium scale and a sufficient number of new islands.
When implementing fractal coastlines, I realized the ability to control the level of fractalization using the noise function, so some areas will have smooth coasts and others complex. I thought that this would greatly increase the interestingness of the map, and it would look less “generated”, so I’ll add this feature here. The idea is quite simple - before adding coastline noise to the map, I multiply it by the output of the second noise function, which varies from zero to 1. Where this function is small, small details will be added to the coastlines. Where it is close to 1, additional details will be added completely. Selecting the scale of the second noise function, which slowly varies throughout the map, I will get some areas with complex coastlines, a part with simple ones, and logical transitions between them:

Here I made the coastal parameters with large values so that the difference would be clearer. We see a wild, indented coast in the northeast, and smoother beaches in the west.
So, we have significantly improved the coastline generation, but I still cannot completely generate a map with so many Delone triangles. I only show the contour maps, because many other map elements are broken. Need to fix it.
The rest of the program does not work well with so many Delone triangles (at current settings of 256K). The main problem is that Dragons Abounddraws land and water by drawing all the individual triangles, and this number of SVG elements causes the browser to crash. So I had to completely turn off sushi rendering. There is probably a way around this problem, but having so many triangles creates other problems. For example, some parts of the program must process the entire map. Each of them becomes at 256K locations sixteen times slower than at 16K locations. There are also parts in the code (for example, a new precipitation model) that break when working with so many triangles. And we don’t gain anything by creating such a detailed grid of locations - after generating the coastline, nothing gets better from the added complexity. So even though I could look at the program and fix those areas
As mentioned above, Azgaar has already done work on changing the resolution of the Voronoi grid underlying the map. He realized the possibility of changing the grid resolution on the fly during the generation process, that is, he could (for example) increase the density of locations along the coast. However, the local density change has its drawbacks - in particular, it creates triangles of a strange shape along the border. Later, Azgaar expressed the opinion that the system is too complex and not worth the effort. Azgaar usually knows what he is talking about, so I will take his word for it, and I will not try to repackage the finished grid.
Instead, I created a second grid with the desired (lower) resolution, and then copied the elevation map to this new grid. (Do not forget that Dragons Aboundnow keeps shorelines separate from the grid, so after they are created, they no longer depend on the exact matching grid. Make it a bit complicated. Since the original grid has a much higher resolution than the new one, many locations in the original grid will be superimposed on one location in the new grid. Each of these source locations has a different height on the height map, how can I copy them? Use the mean? Or the maximum (minimum) height?
For starters, I will simply select one random location to simply see if the new grid will work with the rest of the program:

Everything turned out surprisingly good. A minor bug occurs when new locations are not properly labeled as land, beach or water, but after solving this problem, the card generation worked fine. It is necessary to clean up minor issues (for example, the label Palmanor, which came to water), but on the whole everything looks good. Even the tiny islands turned out beautiful.
In the end, I decided that by reducing the resolution of the Voronoi grid, each location would be the average of the base locations. This seems like a sensible decision, and if necessary it can always be changed. This image shows how, as a result, coastlines are separated from the finished grid:

To summarize: Dragons Abound uses a very high resolution Delone triangle grid to generate a height map. After it is completed, Dragons Abound identifies coastlines, tracking transitions from negative to positive values in the elevation map. Then the game copies the high-resolution grid into a much smaller grid, averaging locations that fall into one location of the new grid. Next, the high resolution grid is discarded, and the rest of the procedural generation and visualization continues on the low resolution grid. An interesting question is whether the use of the Delaunay mesh is of any value at this stage; it may be worth simply copying to a grid of hexagons or something similar.
