The news called on the road: ultrafast energy-efficient optical coprocessor for big data
Last week, Phys.org broke the news : LightOn startup offered an alternative to central processing units (CPUs) and graphics processing units (GPUs) for solving big data analysis tasks. The team of authors is based at the University of Pierre and Marie Curie, the Sorbonne and all other right places in France. The solution is based on optical analog data processing “at the speed of light”. Sounds interesting. Since there were no scientific and technical details in the press release, I had to search for information in patent databases and on university websites. The results of the investigation under the cut.
LightOn's solution is based on a relatively new class of algorithms based on random data projections. Mixing the data in a reproducible and controlled way allows us to extract useful information, for example, for solving classification problems or compressive sensing (I don’t know the Russian term). When working with large amounts of data, the limiting factor is precisely the calculation of random projections. LightOn has developed an optical scheme for calculating random projections and is now receiving funding for the development of a coprocessor that is capable of performing all the hard work of extracting significant features from raw data in streaming mode with minimal energy consumption.
This will allow, for example, replacing graphics processors when processing video and audio data in mobile devices. The optical coprocessor consumes units of watts, and therefore can work in continuous mode, for example, to recognize the sacramental phrase “OK GOOGLE” without additional actions on the part of the user. In the field of big data, the optical coprocessor will help to cope with the exponentially growing volumes of information in such areas as the Internet of things, genome research, video recognition.
How it works?
The article considers the formulation of the ridge regression problem with a simple kernel function, where epsilon is elliptic integrals.

Despite its awesome appearance, this function has a bell-shaped appearance, describes a measure of proximity between feature vectors and is obtained experimentally from an analysis of the optical system.
Ridge regression is one of the simplest linear classifiers; its solution in analytical form depends on the internal product of the matrix of feature vectors XX T with dimension nxn:
Y '= X'X T (XX T + λI) -1 Y
Here X is the matrix of training attributes, Y is the matrix of classification of training data, X 'is the matrix of test attributes, Y' is the desired matrix of classification of test data, I is the identity matrix, λ is the regularization coefficient.
For example, the authors of the article trained the linear ridge regression classifier MNIST in the standard partition n = 60,000 training and 10,000 test samples; classification error was 12%. In this case, inversion of the matrix with a dimension of 60000x60000 was required. Of course, when working with big data, the number of samples can be in the billions, and inverting (and even just storing) matrices of such sizes is impossible.
We now replace X with a nonlinear mapping of random projections of the original features into a space of dimension N <n:
K ij = φ ((WXi ) j + b j ) i = 1..n, j = 1..N
Here W is the matrix of random weights, b is the displacement vector, φ is the nonlinear function. Then, displaying the test signs X 'in K', we get
Y '= K'K T (KK T + λI) -1 Y
When training the MNIST classifier, we took N = 10,000 random projections, W contained random complex weights with the real and imaginary parts, distributed according to Gauss, a module was used as a nonlinear function. Moreover, the classification error was 2% (against 12% in the linear classifier), the dimension of the matrix being reversed was 10,000 x 10,000, moreover, the dimension did not depend on n 2. Using the elliptical kernel function reduces the error to 1.3%. Of course, the use of more advanced classifiers such as convolutional neural networks makes it possible to obtain higher accuracy on MNIST, but neural networks are not always possible in big data problems or mobile applications.
The described mathematical apparatus requires storing and multiplying the original features by a potentially huge random matrix, and applying a nonlinear function to the result of the multiplication. The authors developed an experimental setup that performs these calculations in analog form "at the speed of light."
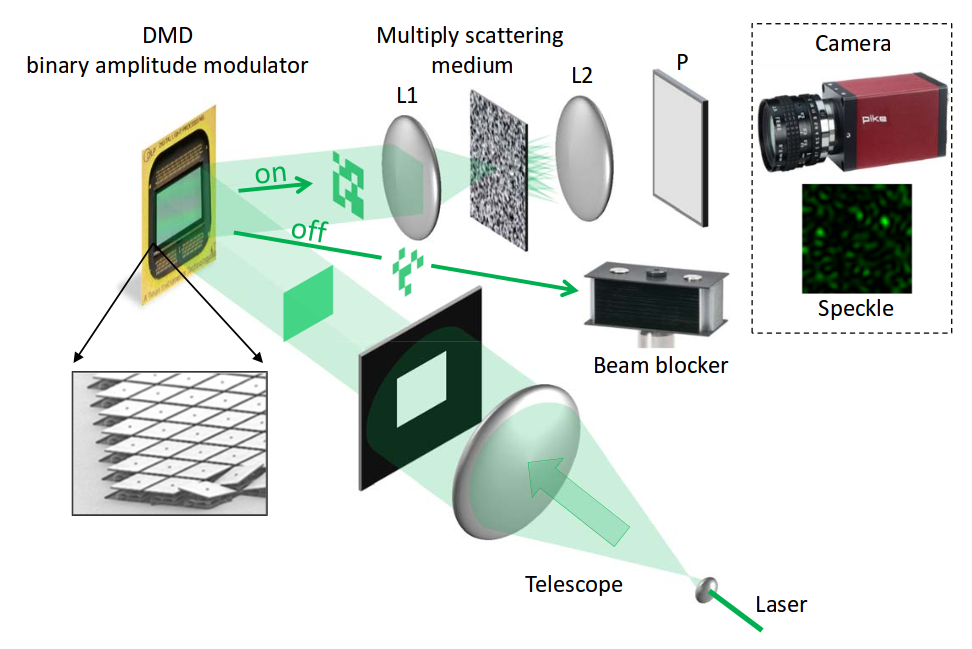
A 532 nm monochrome laser beam is expanded using a “telescope”, and the digital square micromirror array DMD is illuminated with the resulting square beam. DMD spatially encodes a light beam with input data - features. For example, in the case of the MNIST handwritten digit recognition problem, a commercially available DMD matrix of 1920 x 1080 dimensions encodes 28-by-28 MNIST pixels of halftone images in such a way that each MNIST pixel corresponds to a 4 x 4 section of micromirrors, i.e. 16 brightness levels.
Next, the light beam containing the amplitude-modulated signal of the input image is directed to a substance acting as a random projection weight matrix. This is a thick layer (tens of microns) of titanium dioxide nanoparticles, i.e., white pigment. A huge number of opaque particles mix the light beam so that its properties can be considered quite random, but at the same time deterministic and repeatable (i.e., the matrix W is unchanged).
Since the light beam is received from the laser, it is coherent, and generates an interference pattern on the matrix of a conventional video camera. This interference pattern is a set of random projections of high dimension (about 10 4 - 10 6), and therefore it can be used to build a linear classifier, for example SVM. Due to the high dimensionality and non-linearity, the chances of linear separability of the data increase, and linear classifiers based on such interference patterns can achieve accuracy comparable to neural networks. In this case, the calculation speed and energy consumption are not comparable. The speed of operation is limited only by the speed of DMD micromirrors and reading the interference pattern from the video camera. Modern matrices achieve a speed of 20 kHz. The implementation of such an optical system in a single crystal will truly create a universal coprocessor for efficiently extracting features from a variety of data from the surrounding world.
The authors patented the optical circuit for use in the compressive sensing problem (publication WO2013068783) and, possibly, for the classification problem (there is no publication of a patent application yet). Nevertheless, I hope that the described method will give rise to new ideas in habragolov.
If you want to do all kinds of such things, I invite you to an internship or a permanent job at NIKFI - a research and development film and photo institute.
