Solving an equation with integer division without enumeration
Recently , a question has been asked on the Toaster , which touched me in earnest. It goes back to the problem, which I will give here in a slightly different interpretation:
I came to the equation, which in the abstract form looks like (1):
Trying to find an approach without overdoing the solution of such equations, I spent more than one hour, but in the end I found a truly miraculous solution, but the fields of the book are too narrow ;)
Without illusions about the primacy in this matter, I just want to share the pleasure gained in the process. If anyone knows an alternative method or name for it, enlighten me; I appeal to people like me for discussion, and I invite those who are impatient to discuss it under cat.
Consider the resulting equation in this form (2):
since the right-hand side can take only integer values, the whole expression makes sense only when the numerator in the left-hand side is a multiple of the denominator. From this it is obvious that x could have values starting from a value of c and farther with a step a .
Then I considered equation (1) in the form of two functions and . Under what argument they intersect, so will be the decision. For example, I selected small parameter values in such a way as to display the picture as best I can. So, let a = 3, b = 7, c = 9.
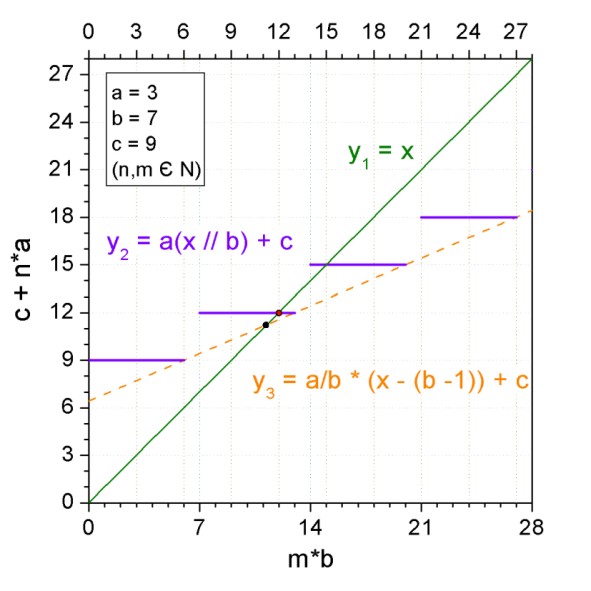
Due to the stepwise nature of the second function, the graphs y1 and y2 intersect at two points: for x1 = 12 and x2 = 15, but according to the condition, we are interested in the first value, as the smaller value. So, in order to determine the intersection area without searching, I introduced the third function - this is just a straight line that limits the function y2 from below and has the equation.
It now remains to find the intersection point of the two straight lines ( y1 and y3 ) and correct the answer from the constraint on the desired x . After all, based on the condition, it can take only those values under which the condition of multiplicity of the numerator is observed in the denominator in equation (2), i.e.where n is a kind of natural factor. To do this, we solve a simple equationand if the resulting root does not meet our requirements, we will shift it to the nearest one. Since the auxiliary function y3 has a positive slope, and all values of y2 are above it, the root adjustment should always be done in a larger direction. So, in our case, straight lines intersect at x = 11.25 (black dot on the graph), and the closest large value satisfying the condition will be 12 (red dot), which is the answer.
Since the Python tag was in question on the Toaster, I’ll give a script below to solve this problem using the function to find the current day’s budget based on the next day’s budget. We use the function as many times as necessary and, voila, we get the answer!
Instead of a conclusion: the
task in this example was determined as the parameter valuesand the equation itself ; The proposed approach with minor changes is applicable in other similar cases - the purpose of the publication was only a description of the principle itself without deriving a universal solution for the general case - so do not judge strictly (including Python code), and have a good Friday!
The programmers somehow passed the project on time and received awards. To celebrate, they kicked off right in PN and bought beer for all the money. On the same day, they all drank, and at VT decided to continue, but there was no more money left. Then they handed over the bottles, added yesterday's surrender, and re-stocked everything, just like yesterday. The same was done on Wed and Thu. And in PT money turned out to be exactly one bottle. They thought about it - they remembered the price of one bottle, how much they took the container (the prices were without kopecks), and nobody could give the amount of money initially. The project was large-scale, the awards are big - so it’s not worth a brute force. What was the minimum budget in PN, so that the events would be formed in this way?Arguing over it as follows
spoiler
поскольку ребята каждый день покупали столько пива, сколько позволял им текущий бюджет (B, budget) – бюджет следующего дня (NB, next_day_budget) формировался из выручки от возврата тары и вчерашней сдачи. Две переменные сложнее одной, потому я перешёл к учёту ежедневного уменьшения бюджета (BL, budget_loss). Причём , где P, price – стоимость одной бутылки пива; R, return – цена тары при возврате, а N – количество приобретённых за день бутылок, такое, что . Тогда, можно заключить следующее:
I came to the equation, which in the abstract form looks like (1):
Trying to find an approach without overdoing the solution of such equations, I spent more than one hour, but in the end I found a truly miraculous solution
Without illusions about the primacy in this matter, I just want to share the pleasure gained in the process. If anyone knows an alternative method or name for it, enlighten me; I appeal to people like me for discussion, and I invite those who are impatient to discuss it under cat.
Consider the resulting equation in this form (2):
since the right-hand side can take only integer values, the whole expression makes sense only when the numerator in the left-hand side is a multiple of the denominator. From this it is obvious that x could have values starting from a value of c and farther with a step a .
Then I considered equation (1) in the form of two functions and . Under what argument they intersect, so will be the decision. For example, I selected small parameter values in such a way as to display the picture as best I can. So, let a = 3, b = 7, c = 9.

Due to the stepwise nature of the second function, the graphs y1 and y2 intersect at two points: for x1 = 12 and x2 = 15, but according to the condition, we are interested in the first value, as the smaller value. So, in order to determine the intersection area without searching, I introduced the third function - this is just a straight line that limits the function y2 from below and has the equation.
It now remains to find the intersection point of the two straight lines ( y1 and y3 ) and correct the answer from the constraint on the desired x . After all, based on the condition, it can take only those values under which the condition of multiplicity of the numerator is observed in the denominator in equation (2), i.e.where n is a kind of natural factor. To do this, we solve a simple equationand if the resulting root does not meet our requirements, we will shift it to the nearest one. Since the auxiliary function y3 has a positive slope, and all values of y2 are above it, the root adjustment should always be done in a larger direction. So, in our case, straight lines intersect at x = 11.25 (black dot on the graph), and the closest large value satisfying the condition will be 12 (red dot), which is the answer.
Since the Python tag was in question on the Toaster, I’ll give a script below to solve this problem using the function to find the current day’s budget based on the next day’s budget. We use the function as many times as necessary and, voila, we get the answer!
defthis_day_budget(next_day_budget):
a = bottle_price - tare_return_price
b = bottle_price
c = next_day_budget
x = (a - a*b + b*c)/(b - a)
if (x - c) % a: # value does not match the increment
x = ((x-c)//a + 1) * a + c
return x
bottle_price = 7
tare_return_price = 4
party_duration_days = 5
last_day_budget = bottle_price
for days_to_party_end in range(party_duration_days):
if days_to_party_end == 0:
current_budget = last_day_budget
else:
current_budget = this_day_budget(current_budget)
print('first day budget was - %d' % current_budget)Instead of a conclusion: the
task in this example was determined as the parameter valuesand the equation itself ; The proposed approach with minor changes is applicable in other similar cases - the purpose of the publication was only a description of the principle itself without deriving a universal solution for the general case - so do not judge strictly (including Python code), and have a good Friday!
