Cryptanalysis "Enigma"

All specialists unanimously agreed that a reading [of the Enigma] is impossible.
Admiral Kurt Fricke, Chief of Naval War Command

Enigma is a rotary cryptographic machine used by Nazi Germany during the Second World War. Thanks to the influence exerted on the course of the war, the hacking of Enigma was perhaps the most striking moment in the long history of cryptanalysis. In this topic, I would like to talk about the hacking method used in Bletchley Park, as well as describe the structure of the machine itself.

Rotary machines

For the first time, encryption rotary machines began to be used at the beginning of the 20th century. The main component of such devices is a disk (aka rotor) with 26 electrical contacts on both sides of the disk. Each contact corresponded to a letter of the English alphabet. The connection of the contacts of the left and right sides implemented a simple replacement cipher. As the disk rotated, the contacts shifted, thereby changing the substitution for each letter. One drive provided 26 different permutations. This means that when encrypting the same character, the resulting sequence begins to be repeated after 26 steps.
To increase the period of the sequence, several rotors connected in series can be used. When making a complete revolution of one of the disks, the next disk is shifted by one position. This increases the length of the sequence to 26 ⁿ , where n is the number of rotors connected in series.
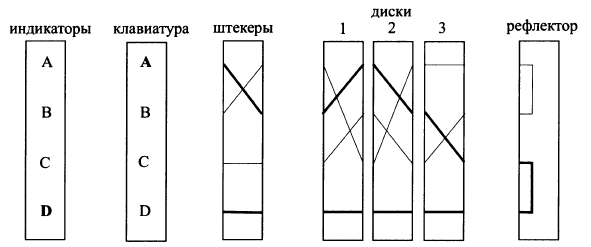
As an example, consider the following image of a simplified rotary machine:

The given machine consists of a keyboard (for entering a character), three disks, an indicator (for displaying crypto text) and implements 4 characters encryption: A, B, C, D. In the initial position, the first disk implements wildcard: AC; BA; CB; DD. Substitutions of the second and third disks are equal to AB; BC; CA; DD and AA; BC; CB; DD respectively.
When the letter B is pressed on the keyboard, an electric circuit is closed, depending on the current position of the rotors, and a light on the indicator lights up. In the above example, the letter B will be encrypted in C. After which the first rotor will shift by one position and the machine settings will take the following form:

Enigma

Enigma is the most popular representative of the world of encryption rotary machines. It was used by German troops during the second world war and was considered practically unbreakable.
The Enigma encryption procedure is implemented as in the above example, with the exception of some additional strokes.
Firstly, the number of rotors in different versions of Enigma could be different. The most common was the Enigma with three rotors, but the four-disc option was also used.
Secondly, the decryption process of the demo rotary machine described above is different from the encryption process. Each time, to decrypt, you will have to swap the left and right rotors, which may not be very convenient. To solve this problem, another disk was added in Enigma, which was called a reflector. In the reflector, all contacts were connected in pairs, thereby realizing the repeated passage of the signal through the rotors, but along a different route. Unlike other rotors, the reflector was always in a fixed position and did not rotate.

Add a reflector that implements the replacement (AB; CD) to our demo encryption machine. When you press the B key, the signal passes through the rotors and enters the reflector through contact C. Here the signal is "reflected" and returns, passing through the rotors in the reverse order and in a different way. As a result, the letter B at the output is converted to D.
Note that if you press the D key, the signal will go along the same circuit, converting D to B. Thus, the presence of a reflector made the encryption and decryption processes identical.
Another Enigma property associated with the reflector is the impossibility of encrypting any letter into itself. This property played a very important role in breaking Enigma.

The resulting device is already very similar to the real Enigma. With one minor caveat. The durability of such a machine rests on the secrecy of the internal switching of the rotors. If the device of the rotors is opened, then hacking is reduced to the selection of their initial positions.
Since each rotor can be in one of 26 positions, for three rotors we get 26 ³ = 17476 options. Moreover, the rotors themselves can also be arranged in random order, which increases the complexity by 3! time. Those. the key space of such a machine will be 6 * 17576 = 105456. This is clearly not enough to ensure a high level of security. Therefore, Enigma was equipped with another additional tool: a patch panel. By connecting letters on the patch panel in pairs, it was possible to add another additional step to encryption.

For example, suppose that the letter B is connected to the letter A on the patch panel. Now, when you press A, AB is substituted first, and the letter B is fed to the input of the first rotor
. The message is decrypted in the same way. When you press D, the rotors and reflector convert DDDDCBAB. Then the patch panel converts B to A.

Enigma Persistence Analysis

The real Enigma differed from the described demo machine in only one. Namely, in the device of the rotors. In our example, the rotor changes its position only when a complete revolution is made by the previous disk. In the real Enigma, each disk had a special recess, which in a certain position picked up the next rotor and shifted it by one position.
The location of the recess for each of the rotors could be adjusted using special outer rings. The initial position of the rings did not affect the switching of the rotors and the encryption result of a single letter, so the rings are not taken into account when calculating the Enigma key space.
So, the basic model of Enigma had 3 different rotors, numbered with Roman numerals I, II, III and implementing the following substitutions:
Entry = ABCDEFGHIJKLMNOPQRSTUVWXYZ
I = EKMFLGDQVZNTOWYHXUSPAIBRCJ
II = AJDKSIRUXBLHWTMCQGZNPYFVOE
III = BDFHJLCPRTXVZNYEIWGAKMUSQ
you can choose from three different encryption sequences.
In addition, each rotor could be installed in one of 26 possible starting positions. Those. the initial position of the rotors has only
6 * 26 ³ = 105456 combinations.
The number of all possible connections on the patch panel is calculated using the formula n! / ((n-2m)! m! 2 ^m ), where n is the number of letters of the alphabet, m is the number of connected pairs.
For 26 letter of the English alphabet and 10 pairs, this is 150738274937250 = 2⁴⁷ different combinations.
Thus, the basic version of the Enigma with three rotors had a solid key space even by modern standards:
150738274937250 * 105456 = 15.896,255,521,782,636,000≈2 ⁶⁴ .
Such a huge number of options inspired a deceptive sense of invulnerability.

Enigma Cryptanalysis

The large key space provides the Enigma cipher with a fairly serious level of resistance to attacks using the well-known ciphertext.
A complete search of 2 ⁶⁴ options, even on modern computers, is not an easy task.
However, everything changes if you apply an attack with known plaintext. For this case, there is a very ingenious method that allows you to neglect the settings of the patch panel in the process of searching for a key combination, which reduces the Enigma key space to only 105,456 combinations and makes the entire cipher fatally vulnerable.

The method exploits the presence of a pair of open-closed text of the so-called "cycles". To explain the concept of “cycle”, consider the following open message P and its corresponding cryptotext C, encrypted by Enigma.

P = WETTERVORHERSAGEBISKAYA
C = RWIVTYRESXBFOGKUHQBAISE
Let's write each character from a pair in the form of a table:

1

2

3

4

5

6

7

8

9

10

eleven

12

thirteen

14

fifteen

16

17

18

19

20

21

22

23

w

e

t

t

e

r

v

o

r

h

e

r

s

a

g

e

b

i

s

k

a

y

a

r

w

i

v

t

y

r

e

s

x

b

f

o

g

k

u

h

q

b

a

i

s

e

Pay attention to the substitutions implemented by the enigma in 14, 15 and 20 positions. At step 14, the letter A is encrypted in G. The latter, in turn, is encrypted in K at step 15. And then the letter K is encrypted in A at step 20, thereby looping through the AGKA chain. Such looped chains are called cycles. The presence of cycles allows us to divide the task of breaking Enigma into two simple components: 1) search for the starting position of the rotors and 2) search for the connections of the patch panel with known rotor settings.

We know that with encryption in Enigma there are several transformations. First, the signal passes through the patch panel. The result of the conversion on the patch panel goes to the rotors. After that, the signal enters the reflector and returns through the rotors to the patch panel, where the last substitution is performed. All these operations can be represented by the mathematical formula:
E _i = S ^-1 R ^-1 TRS, where
S and S ^-1 , are the transformations on the patch panel at the input and output, respectively;
R and R ^-1 - conversion in rotors at the input and output;
T is the conversion on the reflector.
Omitting the patch panel, we express the internal Enigma transformation through P _i :
P _i = R ^-1 TR
Now the encryption can be written as:
E _i = S ^-1 P _i S

Using the formula, we rewrite the substitutions from the example in 14, 15 and 20 positions.
S ^-1 P ₁₄ S (A) = G or what is the same P ₁₄ S (A) = S (G).
P ₁₅ S (G) = S (K)
P ₂₀ S (K) = S (A)
Replacing S (K) in the last expression, we get:
P ₂₀ P ₁₅ P ₁₄S (A) = S (A) (1), where S (A) is the letter connected to A on the patch panel.
Now the attack is reduced to a trivial enumeration of all possible rotor settings. For each combination of rotors, it is necessary to verify the fulfillment of equality (1). If equality is fulfilled for the letter S, this means that the correct rotor configuration is found and that the letter A is connected to the letter S on the patch panel. The search for the remaining pairs is reduced to decrypting the cryptotext by letter and comparing the result with the known plaintext.
It should be noted that with a probability of 1/26, equality can also be fulfilled if rotors are not installed correctly, therefore, to increase the reliability of the algorithm, it is advisable to use several “cycles”.
Another important point is that only part of the encrypted message can be known to the attacker. And in this case, first of all, he will need to find the location of the known text in the received cryptogram. In solving this problem, knowledge of the fact that Enigma never encrypts a letter into itself greatly helps. Those. To find the correct offset, you need to find such a position in the cryptotext at which none of the letters of the closed text is duplicated by the letter of the open message.

PS

A very slow but working implementation of the Python attack can be viewed on GitHub .

References

• Detailed description of Enigma
• Enigma description with examples
• Detailed Turing Bombs
• Great simulator of different versions of Enigma