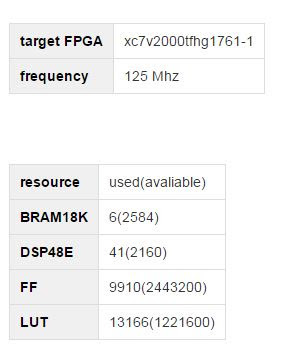
Implementing a FPGA Pseudo Random Number Generator Using Vivado HLS 2014.4
In many problems, it becomes necessary to use a pseudo-random number generator. So we have such a need. In general, the task was to create a computing platform based on the RB8V7 block , which should have been used as an accelerator for calculating a specific scientific problem.
I will say a few words about this scientific task: it was necessary to calculate the dynamics of biological microtubules at times of the order of a minute. The calculations were calculations using the molecular-mechanical model of a microtubule developed in a scientific group. It was planned that on the basis of the obtained calculation results, it will be possible to draw a conclusion about the mechanisms of the dynamic instability of microtubules. The need to use the accelerator was due to the fact that a minute is equivalent to a sufficiently large number of calculation steps (~ 10 ^ 12) and, as a result, a large amount of time spent on calculations.
So, returning to the topic of the article, in our case, pseudorandom number generators were needed to take into account the thermal motion of the molecules of the mentioned microtubules.
The architecture with support for DMA transmissions was used as the basic architecture of the project . As a component of this computing platform, it was necessary to implement an IP core that would be able to generate a new pseudo-random normally distributed number of type float every clock cycle and would take as little resources as possible on the FPGA.
I want to note that, in the end, everything worked out for us, but the path to solving this problem was not without the wrong steps and errors, which I also want to write about below. I hope this article is helpful.
To solve this problem, we used a high-level translator in the RTL code. To implement a complex computational task, this approach allows you to get the result much faster (and often better) than using bare RTL. We used the Vivado HLS program version 2014.4, which translates C / C ++ code using special directives into RTL code. Examples of directives can be found here .
Given the above requirements for the solution being developed and the fact that the generator must include several stages of computation, the pipeline is the most suitable architecture. You can read more about the implementation of the FPGA pipeline here . I want to note that the main characteristics of the computing pipeline are the initialization interval and latency. The initialization interval is the number of ticks spent on the execution of the conveyor step (maximum among all steps).
Latency is the number of clock cycles that have elapsed from the moment the data entered the pipeline input until the output of the result by the pipeline. In this case, latency is not very interesting for us, since it is negligible compared to the estimated total time of the pipeline, but the initialization interval should be taken very carefully, since it actually characterizes how often the pipeline is able to receive data and, accordingly how often he is able to produce a new result.
Initially, it was decided to use the following approach:
Of the advantages of this approach, it is worth noting that this generator of normal numbers is implemented in the final scheme very simply and really does not take very much. The main disadvantage of this approach is that it is incorrect in our case. =) Indeed, the sequential values that the generator gives are correlated. This can be clearly demonstrated by constructing an autocorrelation function (see Fig.), Or by plotting x [i + k] on x [i], where k = 1,2,3 ...
This error resulted in interesting effects in the dynamics of microtubules, the movement of which was modeled using this generator.

So, the algorithm for generating uniformly distributed integers needed to be changed. The choice fell on the Whirlwind of Mersenne . The fact that in this algorithm the values of the generated numbers are not correlated with each other can be seen by looking at the autocorrelation function of the resulting sequence of numbers. However, the implementation of this algorithm requires more resources, since it works with a number field of size 612, and not with a single number as in the previous case (see the code in the public domain ).
Immediately make a reservation that I understand by the words "the procedure takes n cycles (steps)." This means that this procedure during translation to RTL will be performed in n clock pulses. For example, if at the next step in the pipeline we need to read two words from single-port RAM memory, this operation will be performed in two cycles, since the port is only one, that is, the memory can provide for the execution of only one write or read request.
For optimal translation of this algorithm into RTL, the code needed to be processed. Firstly, in the initial implementation inside the generator, the following occurs: when a new random number is requested, the output is either the next matrix element, or, upon reaching the end of the matrix, the matrix elements are updated. The update procedure consists of various bitwise operations using array elements. The procedure takes at least 612 steps, since the value of each element is updated. Then the output is the zero element of the matrix. Thus, the procedure will take a different number of steps for different calls to this function. Such a function cannot be pipelined.
We change this procedure: now, in one call to the function, the previous element of the array is updated and the current element is returned. Now this procedure always takes the same number of measures. Moreover, the result is the same in both implementations: at the end of the matrix traversal, it will already be filled with updated values and you can simply return to the zero element of the array. Now this procedure is really pipelined.
Now we ask ourselves how often such a pipeline will be able to produce a new random number? To do this, we need to bring some additional clarity. With what resources to implement the used array (mt)? It can be implemented either using registers or using memory. Register-based implementation is the easiest in terms of ultimate code optimization to achieve a single initialization interval. Unlike memory cells, each register can be accessed independently.
However, in the case of using a large number of registers, there is a high probability of the appearance of time delays on the paths between the registers, which leads to the need to lower the operating frequency for the generated IP core. In the case of memory use, there is a limit on the number of simultaneous requests to a memory block, the reason for which is the limited number of block ports. However, there are usually no problems with time delays. Due to resource restrictions, in our case it would be preferable to implement the array using memory. Consider whether we have memory access conflicts and whether it is possible to resolve them.
So, how many simultaneous from the FPGA point of view array element requests occur in our cycle? Firstly, we note that on each measure we work with four cells of the array. That is, in a first approximation, we need to provide four simultaneous requests to memory: three reads and one record. Moreover, one reading and one record occur in the same cell.
The first problem that needs to be solved is to remove the read and write conflict in the same cell. This can be done by noticing that as a result of successive calls to the function, reading from the same cell takes place, thus, for the previous call it is enough to read the value and save the read in the register, and on the next just take the required number from the register. Now it is necessary to provide three simultaneous requests to memory: two reads and one record (in different memory cells).
There are several tricks to resolving memory query conflicts in Vivado HLS: first, add a directive that tells the translator to implement the array through dual-port RAM memory, so you can afford two simultaneous requests to the memory block, provided that they do not access to the same cell.
Secondly, there is a directive that tells the translator to implement the array not through one memory block, but after several. This can increase the total number of ports, and thus increase the maximum possible number of simultaneous requests. It is possible, for example, to make the array elements with indices 0 ... N / 2 lie in one memory block, and the elements with indices N / 2 + 1 ... N-1 lie in the second memory block. Or, for example, elements with indices 2 * k lay in one block, and elements with indices 2 * k + 1 lay in another block. I note that the number of blocks can be> 2. It also allows in some cases to increase the number of possible simultaneous requests to the array.
Unfortunately, the last approach in our case was not applicable in its pure form, since it was necessary to break our array into several blocks of unequal size, which the directive does not know how to do. If you carefully look at which elements in the array are accessed during the passage through all indices, you will notice that the array can be divided into three parts so that there are no more than two simultaneous queries to each part.

In fact, this stage took the longest amount of time, because the Vivado HLS translator stubbornly did not want to understand what we want from it and the final initialization interval was more than 1. It helped that we simply presented and drew the final circuit and wrote in accordance with it the code. Earned!
Thus, we implemented our array through 3 blocks of dual-port RAM memory, which allowed us to pipeline our function and provide a single initialization interval. That is, now we have a working generator of uniformly distributed pseudorandom numbers. Now it is necessary to obtain normally distributed pseudorandom numbers from these numbers. One could take the previous approach using the central limit theorem. However, let me remind you that now the generator of uniformly distributed random numbers takes much more resources, and for the central limit theorem it would be necessary to implement 12 such generators.
Our choice fell on the Box-Muller transformation, которое позволяет получить два нормально распределенных случайных числа из двух равномерно распределенных случайных величин на отрезке (0,1]. Причем в отличие от подхода с ЦПТ, где 12 это на самом деле не очень большое число, в случае преобразования мы получаем числа, для которых распределение аналитически точно будет гауссовским. Чуть более подробно об этом можно почитать тут. Хочу только заметить, что данное преобразование существует в двух вариантах: одно использует меньше вычислений, но при этом результат выдается не при каждом вызове генератора, второй подход использует больше вычислений, однако результат гарантирован при каждом вызове.
Since we need the result every step, the second approach was used. In addition, a directive was applied to each computational operation, which instructs the translator NOT to implement this operation using DSP blocks. By default, Vivado HLS implements computational operations using the maximum number of DSP blocks. The fact is that, taking into account pipelining, the number of required DSP blocks would be quite large compared to the total number of available DSP blocks. Given their location on the crystal, large time delays would be obtained.
As a result, we got a kernel using the following approach:
I also cite the visualization of microtubule dynamics using this generator.

PS: In fact, later it turned out that using the Mersenne vortex approach + the Box-Muller transform is indeed a working approach for obtaining normally distributed random numbers [1].
The project is available on github .
I welcome any questions or comments.
[1] High-Performance Computing Using FPGAs Editors: Vanderbauwhede, Wim, Benkrid, Khaled (Eds.) 2013 pp. 20-30
I will say a few words about this scientific task: it was necessary to calculate the dynamics of biological microtubules at times of the order of a minute. The calculations were calculations using the molecular-mechanical model of a microtubule developed in a scientific group. It was planned that on the basis of the obtained calculation results, it will be possible to draw a conclusion about the mechanisms of the dynamic instability of microtubules. The need to use the accelerator was due to the fact that a minute is equivalent to a sufficiently large number of calculation steps (~ 10 ^ 12) and, as a result, a large amount of time spent on calculations.
So, returning to the topic of the article, in our case, pseudorandom number generators were needed to take into account the thermal motion of the molecules of the mentioned microtubules.
The architecture with support for DMA transmissions was used as the basic architecture of the project . As a component of this computing platform, it was necessary to implement an IP core that would be able to generate a new pseudo-random normally distributed number of type float every clock cycle and would take as little resources as possible on the FPGA.
More details
The last requirement was due to the fact that, firstly, in addition to this IP core, other computing modules + interface part should have been present on the FPGA, and secondly, the calculations in the problem were performed on floating-point numbers of type float, which in the case of FPGAs take up quite a lot of resources, and thirdly, several cores were supposed to be on FPGAs. The requirement to generate a random number every cycle was due to the architecture of the final computing module, which, in fact, used these random numbers. The architecture was a conveyor and, accordingly, required new random numbers every cycle.
I want to note that, in the end, everything worked out for us, but the path to solving this problem was not without the wrong steps and errors, which I also want to write about below. I hope this article is helpful.
To solve this problem, we used a high-level translator in the RTL code. To implement a complex computational task, this approach allows you to get the result much faster (and often better) than using bare RTL. We used the Vivado HLS program version 2014.4, which translates C / C ++ code using special directives into RTL code. Examples of directives can be found here .
Given the above requirements for the solution being developed and the fact that the generator must include several stages of computation, the pipeline is the most suitable architecture. You can read more about the implementation of the FPGA pipeline here . I want to note that the main characteristics of the computing pipeline are the initialization interval and latency. The initialization interval is the number of ticks spent on the execution of the conveyor step (maximum among all steps).
Latency is the number of clock cycles that have elapsed from the moment the data entered the pipeline input until the output of the result by the pipeline. In this case, latency is not very interesting for us, since it is negligible compared to the estimated total time of the pipeline, but the initialization interval should be taken very carefully, since it actually characterizes how often the pipeline is able to receive data and, accordingly how often he is able to produce a new result.
Initially, it was decided to use the following approach:
- linear feedback shift registers to obtain independent integers of uniformly distributed random numbers. At the beginning, each of them is initiated using its "seed" number, the so-called seed.
- the central limit theorem, which allows us to state that the sum of a large number of independent random variables has a distribution close to normal. In our case, 12 numbers are summed.
The code
#pragma HLS PIPELINE
unsigned lsb = lfsr & 1;
lfsr >>= 1;
if (lsb == 1)
lfsr ^= 0x80400002;
return lfsr;
Of the advantages of this approach, it is worth noting that this generator of normal numbers is implemented in the final scheme very simply and really does not take very much. The main disadvantage of this approach is that it is incorrect in our case. =) Indeed, the sequential values that the generator gives are correlated. This can be clearly demonstrated by constructing an autocorrelation function (see Fig.), Or by plotting x [i + k] on x [i], where k = 1,2,3 ...
Autocorrelation function

This error resulted in interesting effects in the dynamics of microtubules, the movement of which was modeled using this generator.

So, the algorithm for generating uniformly distributed integers needed to be changed. The choice fell on the Whirlwind of Mersenne . The fact that in this algorithm the values of the generated numbers are not correlated with each other can be seen by looking at the autocorrelation function of the resulting sequence of numbers. However, the implementation of this algorithm requires more resources, since it works with a number field of size 612, and not with a single number as in the previous case (see the code in the public domain ).
autocorrelation function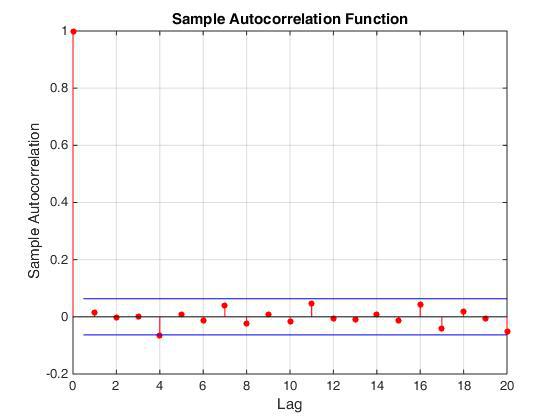

Immediately make a reservation that I understand by the words "the procedure takes n cycles (steps)." This means that this procedure during translation to RTL will be performed in n clock pulses. For example, if at the next step in the pipeline we need to read two words from single-port RAM memory, this operation will be performed in two cycles, since the port is only one, that is, the memory can provide for the execution of only one write or read request.
For optimal translation of this algorithm into RTL, the code needed to be processed. Firstly, in the initial implementation inside the generator, the following occurs: when a new random number is requested, the output is either the next matrix element, or, upon reaching the end of the matrix, the matrix elements are updated. The update procedure consists of various bitwise operations using array elements. The procedure takes at least 612 steps, since the value of each element is updated. Then the output is the zero element of the matrix. Thus, the procedure will take a different number of steps for different calls to this function. Such a function cannot be pipelined.
Option 0
unsigned long y;
if (mti >= N) { /* generate N words at one time */
int kk;
if (mti == N+1) /* if sgenrand() has not been called, */
sgenrand(4357); /* a default initial seed is used */
for (kk=0;kk> 1) ^ mag01[y & 0x1];
}
for (;kk> 1) ^ mag01[y & 0x1];
}
y = (mt[N-1]&UPPER_MASK)|(mt[0]&LOWER_MASK);
mt[N-1] = mt[M-1] ^ (y >> 1) ^ mag01[y & 0x1];
mti = 0;
}
y = mt[mti++];
y ^= (y >> 11);
y ^= (y << 7) & 0x9d2c5680UL;
y ^= (y << 15) & 0xefc60000UL;
y ^= (y >> 18);
return ( (double)y * 2.3283064370807974e-10 ); /* reals */
/* return y; */ /* for integer generation */
We change this procedure: now, in one call to the function, the previous element of the array is updated and the current element is returned. Now this procedure always takes the same number of measures. Moreover, the result is the same in both implementations: at the end of the matrix traversal, it will already be filled with updated values and you can simply return to the zero element of the array. Now this procedure is really pipelined.
Option 1
#pragma HLS PIPELINE
#pragma HLS INLINE
float y;
unsigned long mt_temp,reg1;
unsigned long temper, temper1;
if (mti> 1) ^ mag01[mt_temp & 0x1UL];
}else{
if (mti> 1) ^ mag01[mt_temp & 0x1UL];
}else{
mt_temp = (mt[N_period-1]&UPPER_MASK)|(mt[0]&LOWER_MASK);
mt[N_period-1] = mt[M_period-1] ^ (mt_temp >> 1) ^ mag01[mt_temp & 0x1UL];
}
}
reg1 = mt[mti];
if (mti == (N_period - 1)) mti = 0;
else mti=mti+1;
temper=tempering(reg1);
temper1 = (temper==0) ? 1 : temper;
y=(float) temper1/4294967296.0;
return y;
Now we ask ourselves how often such a pipeline will be able to produce a new random number? To do this, we need to bring some additional clarity. With what resources to implement the used array (mt)? It can be implemented either using registers or using memory. Register-based implementation is the easiest in terms of ultimate code optimization to achieve a single initialization interval. Unlike memory cells, each register can be accessed independently.
However, in the case of using a large number of registers, there is a high probability of the appearance of time delays on the paths between the registers, which leads to the need to lower the operating frequency for the generated IP core. In the case of memory use, there is a limit on the number of simultaneous requests to a memory block, the reason for which is the limited number of block ports. However, there are usually no problems with time delays. Due to resource restrictions, in our case it would be preferable to implement the array using memory. Consider whether we have memory access conflicts and whether it is possible to resolve them.
So, how many simultaneous from the FPGA point of view array element requests occur in our cycle? Firstly, we note that on each measure we work with four cells of the array. That is, in a first approximation, we need to provide four simultaneous requests to memory: three reads and one record. Moreover, one reading and one record occur in the same cell.
Option 2
#pragma HLS PIPELINE
#pragma HLS INLINE
float y;
unsigned long mt_temp,reg1,reg2,reg3,result;
unsigned long temper, temper1;
if (mti> 1) ^ mag01[mt_temp & 0x1UL];
mt[mti]=result; //write
if (mti == (N_period - 1)) mti = 0;
else mti=mti+1;
temper=tempering(result);
temper1 = (temper==0) ? 1 : temper;
y=(float) temper1/4294967296.0;
return y;
The first problem that needs to be solved is to remove the read and write conflict in the same cell. This can be done by noticing that as a result of successive calls to the function, reading from the same cell takes place, thus, for the previous call it is enough to read the value and save the read in the register, and on the next just take the required number from the register. Now it is necessary to provide three simultaneous requests to memory: two reads and one record (in different memory cells).
Option 3
#pragma HLS PIPELINE
#pragma HLS INLINE
float y;
unsigned long mt_temp,reg1,reg2,reg3,result;
unsigned long temper, temper1;
if (mti> 1) ^ mag01[mt_temp & 0x1UL];
mt[mti]=result; //write
prev_val=reg2;
if (mti == (N_period - 1)) mti = 0;
else mti=mti+1;
temper=tempering(result);
temper1 = (temper==0) ? 1 : temper;
y=(float) temper1/4294967296.0;
return y;
There are several tricks to resolving memory query conflicts in Vivado HLS: first, add a directive that tells the translator to implement the array through dual-port RAM memory, so you can afford two simultaneous requests to the memory block, provided that they do not access to the same cell.
#pragma HLS RESOURCE variable=mt1 core=RAM_2P_BRAM
Secondly, there is a directive that tells the translator to implement the array not through one memory block, but after several. This can increase the total number of ports, and thus increase the maximum possible number of simultaneous requests. It is possible, for example, to make the array elements with indices 0 ... N / 2 lie in one memory block, and the elements with indices N / 2 + 1 ... N-1 lie in the second memory block. Or, for example, elements with indices 2 * k lay in one block, and elements with indices 2 * k + 1 lay in another block. I note that the number of blocks can be> 2. It also allows in some cases to increase the number of possible simultaneous requests to the array.
#pragma HLS array_partition variable=AB block factor=4
Unfortunately, the last approach in our case was not applicable in its pure form, since it was necessary to break our array into several blocks of unequal size, which the directive does not know how to do. If you carefully look at which elements in the array are accessed during the passage through all indices, you will notice that the array can be divided into three parts so that there are no more than two simultaneous queries to each part.

In fact, this stage took the longest amount of time, because the Vivado HLS translator stubbornly did not want to understand what we want from it and the final initialization interval was more than 1. It helped that we simply presented and drew the final circuit and wrote in accordance with it the code. Earned!
Scheme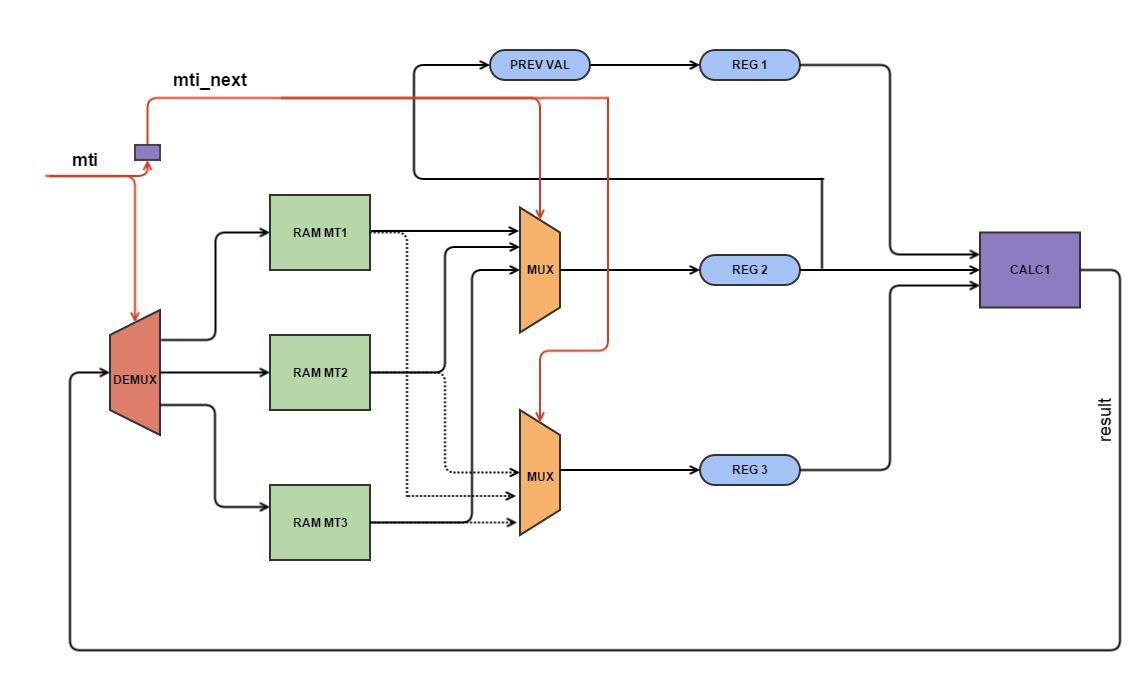

Final version
#pragma HLS PIPELINE
#pragma HLS RESOURCE variable=mt1 core=RAM_2P_BRAM
#pragma HLS RESOURCE variable=mt2 core=RAM_2P_BRAM
#pragma HLS RESOURCE variable=mt3 core=RAM_2P_BRAM
#pragma HLS INLINE
float y;
unsigned long mt_temp,reg1,reg2,reg3,result, m1_temp,m2_temp, m3_temp;
unsigned long temper, temper1;
unsigned int a1,a2, a3,s2,s3;
int mti_next=0;
if (mti == (N_period - 1)) mti_next = 0;
else mti_next=mti+1;
if (mti_next==0) {
s2=1; s3=2;
a1=mti_next; a2=2*M_period-N_period-1; a3=0;
}
else if (mti_next < (N_period - M_period)) {
s2 = 1; s3 = 3;
a1 = mti_next; a2 = 0; a3 = mti_next-1;
}else if (mti_next== (N_period - M_period)){
s2 = 2; s3 = 3;
a2 = 0; a1 = 0; a3 = N_period-M_period-1;
}
else if (mti_next < M_period) {
s2 = 2; s3 = 1;
a1 = mti_next - (N_period - M_period)-1; a2 = mti_next - (N_period - M_period); a3 = 0;
} else if (mti_next < (2*(N_period-M_period)+1)) {
s2 = 3; s3 = 1;
a1 = mti_next - (N_period - M_period)-1; a2 = 0; a3 = mti_next - M_period;
} else {
s2 = 3; s3 = 2;
a1 = 0; a2 = mti_next - (2*(N_period-M_period)+1); a3 = mti_next - M_period;
}
// read data from bram
m1_temp = mt1[a1];
m2_temp = mt2[a2];
m3_temp = mt3[a3];
if (s2 == 1) reg2 = m1_temp;
else if (s2 == 2) reg2 = m2_temp;
else reg2 = m3_temp;
if (s3 == 1) reg3 = m1_temp;
else if (s3 == 2) reg3 = m2_temp;
else reg3 = m3_temp;
reg1 = prev_val;
mt_temp = (reg1&UPPER_MASK)|(reg2&LOWER_MASK);
result = reg3 ^ (mt_temp >> 1) ^ mag01[mt_temp & 0x1UL];
// write process
if (mti < (N_period - M_period))
mt1[mti] = result;
else if (mti < M_period)
mt2[mti-(N_period-M_period)] = result;
else
mt3[mti-M_period] = result;
//save into reg
prev_val=reg2;
mti=mti_next;
temper=tempering(result);
temper1 = (temper==0) ? 1 : temper;
y=(float) temper1/4294967296.0;
return y;
Thus, we implemented our array through 3 blocks of dual-port RAM memory, which allowed us to pipeline our function and provide a single initialization interval. That is, now we have a working generator of uniformly distributed pseudorandom numbers. Now it is necessary to obtain normally distributed pseudorandom numbers from these numbers. One could take the previous approach using the central limit theorem. However, let me remind you that now the generator of uniformly distributed random numbers takes much more resources, and for the central limit theorem it would be necessary to implement 12 such generators.
Our choice fell on the Box-Muller transformation, которое позволяет получить два нормально распределенных случайных числа из двух равномерно распределенных случайных величин на отрезке (0,1]. Причем в отличие от подхода с ЦПТ, где 12 это на самом деле не очень большое число, в случае преобразования мы получаем числа, для которых распределение аналитически точно будет гауссовским. Чуть более подробно об этом можно почитать тут. Хочу только заметить, что данное преобразование существует в двух вариантах: одно использует меньше вычислений, но при этом результат выдается не при каждом вызове генератора, второй подход использует больше вычислений, однако результат гарантирован при каждом вызове.
Since we need the result every step, the second approach was used. In addition, a directive was applied to each computational operation, which instructs the translator NOT to implement this operation using DSP blocks. By default, Vivado HLS implements computational operations using the maximum number of DSP blocks. The fact is that, taking into account pipelining, the number of required DSP blocks would be quite large compared to the total number of available DSP blocks. Given their location on the crystal, large time delays would be obtained.
#pragma HLS RESOURCE variable=d0 core=FMul_nodsp
As a result, we got a kernel using the following approach:
- two generators of uniformly distributed random numbers using the Mersenne vortex algorithm
- Box-Muller transform, which of two randomly distributed uniformly distributed over the interval (0,1) receives two normally distributed random numbers

I also cite the visualization of microtubule dynamics using this generator.

PS: In fact, later it turned out that using the Mersenne vortex approach + the Box-Muller transform is indeed a working approach for obtaining normally distributed random numbers [1].
The project is available on github .
I welcome any questions or comments.
[1] High-Performance Computing Using FPGAs Editors: Vanderbauwhede, Wim, Benkrid, Khaled (Eds.) 2013 pp. 20-30
