Augmented Reality on Qt

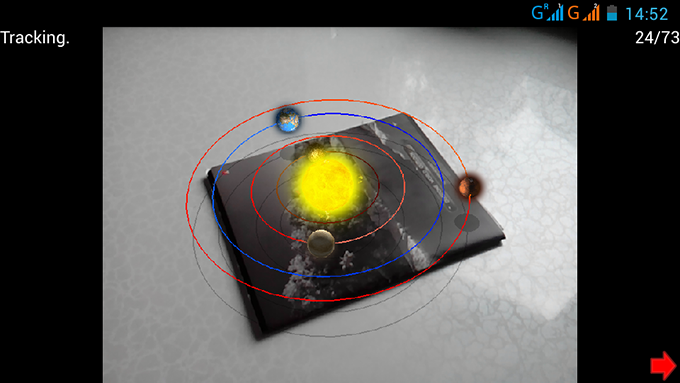
Now augmented reality is one of the most interesting areas. Therefore, I took up its study, and the result was my own implementation of cross-platform markerless augmented reality on Qt. This article will discuss how it was implemented (or how to implement it yourself). Under the cut, you can find a demo and a link to the project on the github.

For the operation of augmented reality does not require any markers, any picture will do. All you need to do is initialize: point the camera at a point in the picture, press the start button and move the camera around the selected point.
Here you can download demos for Windows and Android (for some reason it does not work on windows 10).

about the project

The project is divided into three parts:
AR - everything related to augmented reality here. Everything is hidden in the AR namespace, ARSystem is the main object of the system, in which all the calculations are carried out.
QScrollEngine is a graphics engine for Qt. Located in the namespace - QScrollEngine. There is a separate project on the github .

App - the application that uses the augmented reality system and the graphics engine is described here.
Everything described below is based on the PTAM and SVO projects : Fast Semi-Direct Monocular Visual Odometry .

Input data

The input is a video stream. In this case, we mean a video stream as a sequence of frames where the information from frame to frame does not change very much (which allows us to determine the correspondence between frames).

Qt defines classes for working with a video stream, but they do not work on mobile platforms. But you can make it work. It describes how, in this article I will not dwell on this.

General algorithm of work

Most often, for the operation of augmented reality, some markers are used to help determine the position of the camera in space. This limits its use, since, firstly, markers must be constantly in the frame, and secondly, they must first be prepared (printed). However, there is an alternative - the structure from motion technique, in which data on the position of the camera is found only by moving the image points along the frames of the video stream.

Working with all image points at once is complicated (although it is quite possible ( DTAM )), but you need to simplify it to work on mobile platforms. Therefore, we will simply highlight individual “special” points in the image and monitor their movements. There are many ways to find “special” points. I used FAST. This algorithm has a drawback - it finds angles of only a given size (9, 10 pixels). So that he finds points of different scales, a pyramid of images is used. In short, an image pyramid is a collection of images where the first image (base) is the original image and the next level image is half the size. Finding singular points at different levels of the pyramid, we find "singular" points of different scales. And the pyramid itself is also used in the optical stream to obtain the trajectories of our points. You can read about it here and here .

So, we have the trajectories of the points and now we need to somehow determine the position of the camera in space from them. To do this, as can be understood from the application, initialization is initially carried out in two frames, in which the camera is aimed at approximately the same point, only at different angles. At this moment, the position of the camera in these frames and the position of the "special" points are calculated. Further, according to the known three-dimensional coordinates of the points, you can already calculate the camera position in each next frame of the video stream. For more stable operation, add new points to the tracking process, making a map of the space that the camera sees.

Convert to screen coordinates

To begin with, we’ll deal with how the three-dimensional coordinates of “special” points go into screen coordinates. To do this, we use this formula (we denote it as formula 1):

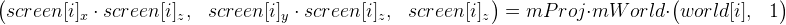
world [i] - these are “special” points in world coordinates. In order not to complicate your life, suppose that these coordinates do not change throughout the entire time. Prior to initialization, these coordinates are not known.
screen [i] - the x and y components are the coordinates of the “special” point in the image (they are given to us by the optical flux), z is the depth relative to the camera. All these coordinates will already be their own on each frame of the video stream.
mProj is a 3 by 3 projection matrix and has the form 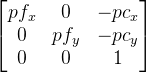, here pf is the focal length of the camera in pixels, pc- The optical center of the camera is also in pixels (usually around the center of the image). It is clear that this matrix should be formed for the camera parameters (its viewing angle).
mWorld is a matrix describing the transformation of points that are 3 by 4 in size (that is, from the usual world matrix from which the last line ( 0 0 0 1 ) was removed . This matrix contains information about the movement and rotation of the camera. And this is what actually first of all we are looking at every frame.
in this case, do not take into account the distortion , but we assume that it is almost not affected, and can be neglected.

we can simplify the formula for getting rid of matrix mProj (in formula 1)

.
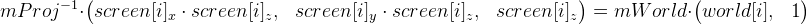
we introduce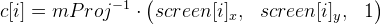which we consider in advance. Then formula 1 is simplified to (let it be formula 2).

Initialization

As already mentioned, the initialization takes place in two frames. We denote them as A and B. Therefore, the matrices 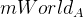and will appear . The points c [i] on frames A and B are denoted by cA [i] and cB [i] . Since we ourselves are free to choose the origin, we assume that the camera in frame A is exactly there, therefore it 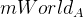is a unit matrix (only 3 by 4 in size). But the matrix will still have to be calculated. And this can be done with the help of points located on the same plane. The following formula will be valid for them:,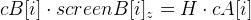
where the matrix H is a plane homography .
We rewrite the expression in this way (removing the index i for clarity):



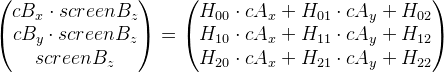
And now for this kind of getting rid of :



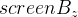Representing the matrix H as a vector 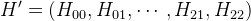, we can represent these equations in matrix form

.

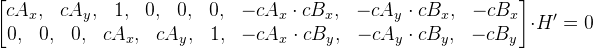We denote the new matrix as M. We get M * H ' = 0. All this was painted for only one point, so there are only 2 rows in the matrix M. In order to find the matrix H ' , it is necessary that the number of rows in the matrix M be greater than or equal to the number of columns. If we have only four points, then you can simply add another row of zeros, a matrix of size 9 by 9 will come out. Next, using the singular expansion, we find the vector H ' (by itself it should not be zero). Vector H '- this, as we recall, is a vector representation of the matrix H , so we now have this matrix.
But as mentioned above, all this is true only for points located on the same plane. And which of them are located and which are not, we do not know in advance, but can guess using the Ransac method this way:

1. In a loop, with a predetermined number of iterations (say 500), we perform the following actions:
   
   • Randomly select four pairs of frame points A and B.
   • We find the matrix H .
   • We consider how many points give an error less than a given value, that is, let the 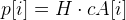condition - be satisfied even then .
   
   
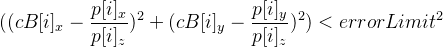2. We select H at that iteration in which the most points turned out.

The matrix H can be obtained using the function from the OpenCV library - cvFindHomography.

From the matrix H, we now obtain the position transition matrix from frame A to frame B and call it mMotion .
To begin, perform singular value decomposition of the matrix H . We obtain three matrices: 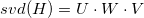. We introduce some values ​​in advance:
- in the end, it should be equal to ± 1;





Arrays (or vectors) indicating the desired character:


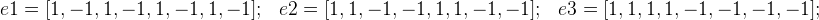
And from then on we can get 8 options mMotion :




;

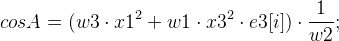
where R [i] is the rotation matrix,
t [i] is the displacement vector.

And matrices 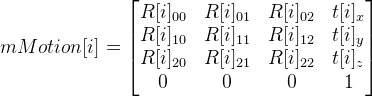. Parameter i= 0, ..., 7, and accordingly we get 8 variants of the matrix mMotion .
In general, we have the following relationship: = mMotion [i] * , since it is a unit matrix, then = mMotion [i] comes out .
It remains to choose one matrix from 8mi mMotion [i] . It is clear that if you release the rays from the points of the first and second frame, then they must intersect, and in front of the camera, both in the first and in the second case. So, we count the number of intersection points in front of the camera in the first and second frame using the resulting mMotion [i], and discard the options in which the number of points will be less. Leaving a couple of matrices in the end, choose the one that gives fewer errors.
So, we have matrices 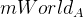and , now knowing them, you can find the world coordinates of points by their projections.

Calculation of world coordinates of a point on several projections

One could use the least squares method, but in practice the following method worked better for me:
Let's go back to formula 2. We need to find the world point , which we denote by a . Suppose we have frames in which the mWorld matrices are known (we denote them as mW [0], mW [1], ... ) and the coordinates of the projections of the point a are known (we take immediately from [0], from [1], ... ).
And then we have such a system of equations:


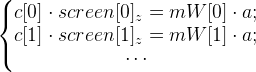
But you can imagine them in this form, getting rid of 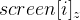(similar to what you did earlier):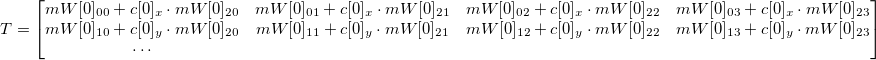


where s is any number not equal to zero,
is the system of equations in matrix form. T- it is known, f - it is necessary to calculate in order to find a.
Solving this equation with the help of a singular expansion (just as we found H ' ), we obtain the vector f . And accordingly the point .

Calculation of the camera position using known world coordinates of points

An iterative algorithm is used. The initial approximation is the previous result of the determination. At each iteration:

1. We carry more points 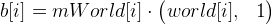. Ideally, points c [i] should be equal to points b [i] , since the current approximation of mWorld is only an approximation (plus other calculation errors), they will differ. We calculate the error vector as follows: 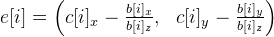. We solve the system of equations by the least squares method: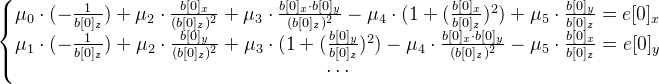
   
   
   It is necessary to find a six-dimensional vector - an exponent vector.
2. We find the displacement matrix from the vector : dT = exp_transformMatrix (mu).
   
   The code for this function is:

   TMatrix exp_transformMatrix(const TVector& mu)
   {
       //Вектор mu - 6-мерный вектор 
       TMatrix result(4, 4);//создаем матрицу 4 на 4
       static const float one_6th = 1.0f / 6.0f;
       static const float one_20th = 1.0f / 20.0f;
       TVector w = mu.slice(3, 3);//получаем последние 3 элемента вектора mu 
       TVector mu_3 = mu.slice(0, 3);//получаем первые 3 элемента вектора mu
       float theta_square = dot(w, w);//dot - скалярное произведение векторов
       float theta = std::sqrt(theta_square);
       float A, B;
       TVector crossVector = cross3(w,  mu.slice(3));//cross3 векторное произведение 2х 3х-мерных векторов
       if (theta_square < 1e-4) {
           A = 1.0f - one_6th * theta_square;
           B = 0.5f;
           result.setColumn(3, mu_3 + 0.5f * crossVector);//устанавливаем 4ый столбец матрицы
       } else {
           float C;
           if (theta_square < 1e-3) {
               C = one_6th * (1.0f - one_20th * theta_square);
               A = 1.0f - theta_square * C;
               B = 0.5f - 0.25f * one_6th * theta_square;
           } else {
               float inv_theta = 1.0f / theta;
               A = std::sin(theta) * inv_theta;
               B = (1.0f - std::cos(theta)) * (inv_theta * inv_theta);
               C = (1.0f - A) * (inv_theta * inv_theta);
           }
           result.setColumn(3, mu_3 + B * crossVector + C * cross3(w,  crossVector));
       }
       exp_rodrigues(result, w, A, B);
       result(3, 0) = 0.0f;
       result(3, 1) = 0.0f;
       result(3, 2) = 0.0f;
       result(3, 3) = 1.0f;
       return result;
   }
   void exp_rodrigues(TMatrix& result, const TVector& w, float A, float B)
   {   
       float wx2 = w(0) * w(0);
       float wy2 = w(1) * w(1);
       float wz2 = w(2) * w(2);
       result(0, 0) = 1.0f - B * (wy2 + wz2);
       result(1, 1) = 1.0f - B * (wx2 + wz2);
       result(2, 2) = 1.0f - B * (wx2 + wy2);
       float a, b;
       a = A * w(2);
       b = B * (w(0) * w(1));
       result(0, 1) = b - a;
       result(1, 0) = b + a;
       a = A * w(1);
       b = B * (w(0) * w(2));
       result(0, 2) = b + a;
       result(2, 0) = b - a;
       a = A * w(0);
       b = B * (w(1) * w(2));
       result(1, 2) = b - a;
       result(2, 1) = b + a;
   }
   

   
   
3. Updating the matrix .

10-15 iterations are enough. Nevertheless, you can insert some additional condition that deduces from the loop if the mWorld value is already close enough to the desired value.
As you determine the position on each frame, some points will be lost, which means that you need to look for lost points. Also, it will not hurt to search for new points that you can focus on.

Bonus - three-dimensional reconstruction

If you can find the position of individual points in space, so why not try to determine the position of all visible points in space? In real time, doing this is too expensive. But you can try to record, and perform the reconstruction later. Actually, I tried to implement this. The result is clearly not perfect, but something comes out:



Link to the source code on github .

UPD: Updated the version for windows, so if your previous version didn’t work, this one will probably work. Plus added the ability to select a camera (if there are several).