Who presses better, or Walsh vs Fourier
Despite the development of science and technology, information compression still remains one of the urgent tasks, where video information compression algorithms occupy a special place. This post will focus on compressing static color images with JPEG-like algorithms.
First, I want to thank the author of the articles “Decoding JPEG for Dummies” and “Inventing JPEG” , which helped me a lot in writing this publication. When I started studying the problems of lossy image compression algorithms, I was constantly tormented by the question regarding the JPEG algorithm: “Why is the role of the basic transformation in the JPEG algorithm assigned to the particular case of the Fourier transform?” Herethe author gives an answer to this question, but I decided to approach it not from the point of view of theory, mathematical models or software implementation, but from the point of view of circuitry.
The JPEG image compression algorithm is a digital signal processing algorithm that, as a rule, is implemented in hardware either on digital signal processors or on programmable logic integrated circuits. In my case, the choice for the digital signal processor to work would mean coming to what I was trying to get away from - a software implementation, so it was decided to focus on programmable logic.
In one of the online stores I purchased a fairly simple debug board, which contains Altera FPGA Cyclone 4 -EP4CE6E22 FPGAs and 512Kx8 SRAM. Since the FPGA was Altera, it was decided to use Quartus II Web Edition for development. The development of individual functional blocks of the hardware codec was carried out in the Verilog language , and the assembly into a single circuit was carried out in the graphical editor of the Quartus II Web Edition environment.
To communicate with a personal computer (receiving commands, receiving / transmitting processed data), in Verilog language I wrote a simple asynchronous UART transceiver . To connect to the COM-port ( RS-232 ) of the computer, based on the MAX3232WE chip and from what was at hand, the level converter was hastily soldered. In the end, here's what happened:

To send commands from a personal computer, as well as transmit / receive data, we used the trial version of the ADVANCED SERIAL PORT MONITOR program , which allows you to generate not only individual data byte packets, but also generate data streams from file contents, as well as write received data streams to a file, which allowed you to send and receive files. I don’t use and control any protocols and checksums for receiving / transmitting data via UART (I was just too lazy to foresee and implement all this), during the connection for receiving / transmitting I used what is called “raw data”.
All arithmetic operations associated with fractional numbers in the codec are carried out in a fixed-point format., addition and subtraction operations are carried out in an additional code , in principle, this is already understandable. How bit depth of the processed data was determined will be described below.
The compression operation is performed on the original images presented in .bmp format with a color depth of 24 bits per pixel (8 bits for each of the color components).
The memory on the debug board was organized as follows: addresses 00000h through 3FFFFh (in hexadecimal notation) are allocated for storing the source data (a picture in .bmp format for compression, or encoded data for decompression), total 256 KB, the remaining 256 KB is the space for recording the data received as a result of compression or decompression, these are addresses from 40000h to 7FFFFh. I think it is obvious that the maximum size of compressed images is limited by the amount allocated for storing data, memory.
The device’s operation algorithm is as follows: immediately after power is supplied, the codec expects a UART data stream, any received data is interpreted here as the source file for processing, if the pause between bytes is 10 ms, then this is interpreted as the end of the file, and the one after the pause bytes received via UART are perceived by the device as a command. Commands are specific byte values. For example, after receiving the file after 10 ms, received in the codec via UART, the value of the AAh byte is interpreted by the device as a command by which the data from the memory microcircuit is transmitted via UART to the computer, starting from the address 40000h and until the value of the address at which the processing of recorded data ended , i.e. The results of compression / decompression are transferred to the computer. The value EEh is interpreted as an image compression / decompression command,
As for the structure of the file with the squeezed image, I decided not to bother, and, unlike the JPEG algorithm, the algorithm I implement is pretty narrow-minded and is not designed for all occasions, so the data obtained as a result of compression is unified the stream is written to the allocated memory area. The only thing that needs to be noted here, in order not to implement the header generator of the .bmp file (it was also laziness), during compression it is simply completely rewritten to the initial (from address 40000h) memory area allocated for the final data, and then, starting from the offset from which the pixel data is stored in the original .bmp file, compressed data is recorded. This offset is stored in the header of the .bmp file at 0Ah relative to its beginning, and is usually 36h. When unpacking,
So, image compression with JPEG-like algorithms is carried out in the following sequence:
Unpacking is in the reverse order.
Of all the above steps, in the codec, I did not implement sub-sampling, since I considered it superfluous (maybe I'm wrong).
Based on the above sequence of actions, I developed the following codec functional diagram:
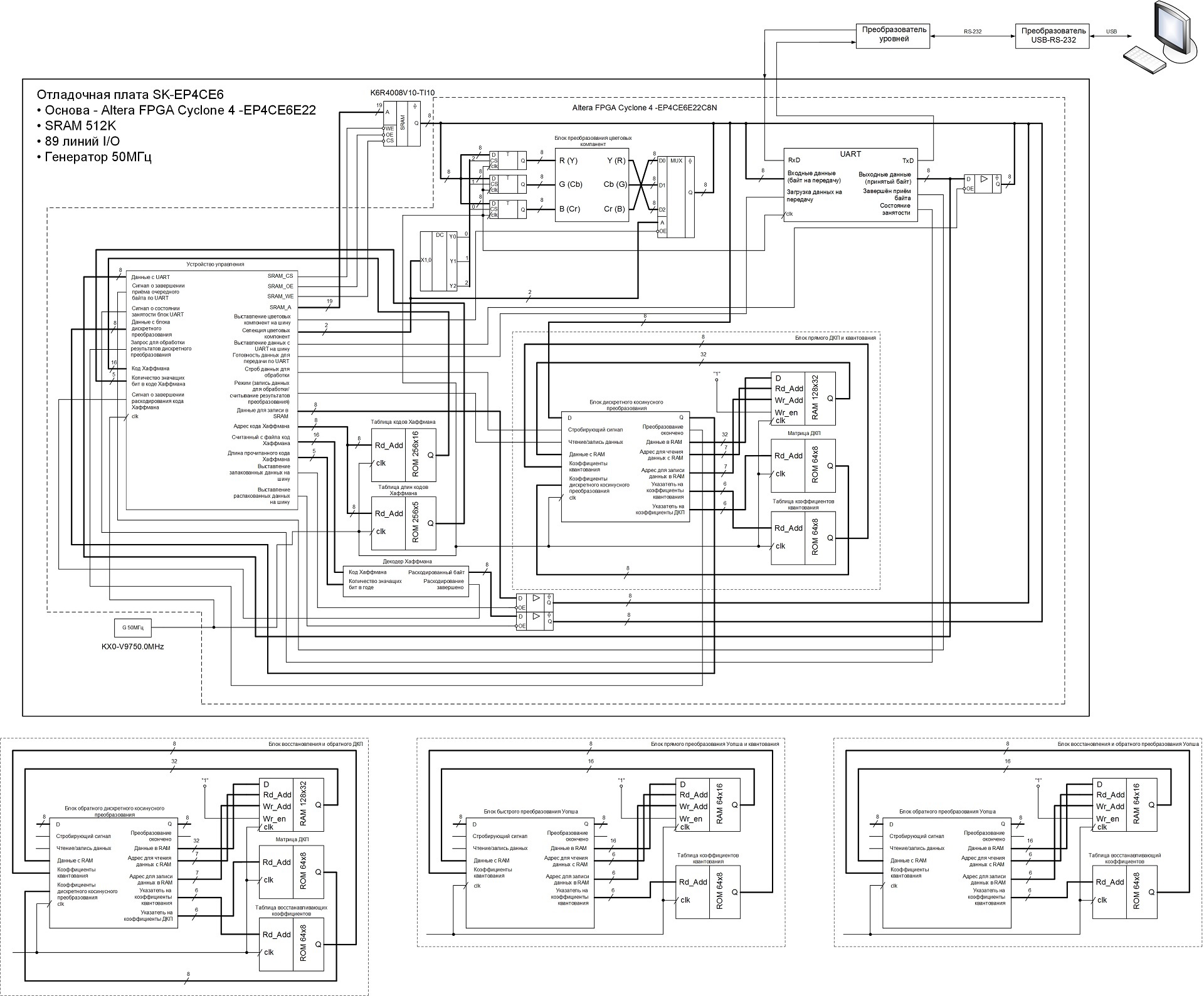
The codec operation process is controlled by a control device, which is a finite state machine, encoding / decoding of series lengths, as well as the generation of final data from Huffman codes during compression and the formation of Huffman codes from the SRAM data received during unpacking. The control device also generates control signals for other operating units.
Under the main scheme, the operating unit schemes are presented, changing which in the main scheme, I changed the operating modes of the device. There was an attempt to assemble everything into a single device and set the codec's operating modes, as well as basic conversion methods using UART commands, but the FPGA logical capacity was not enough. Therefore, the operating modes of the device are changed by changing the corresponding operating units and the task of certain parameters in the control device (including the size of the compressed / unpacked image), after which the changed project is compiled and flashed into the FPGA.
On the Internet you can find a lot of different information on the conversion of color spaces, so immediately start with a description of the hardware implementation.
The color space conversion unit is a combinational logic, due to which the color components are converted in one clock cycle of the generator. The conversion of the RGB color space to YCbCr is carried out according to the following formulas:

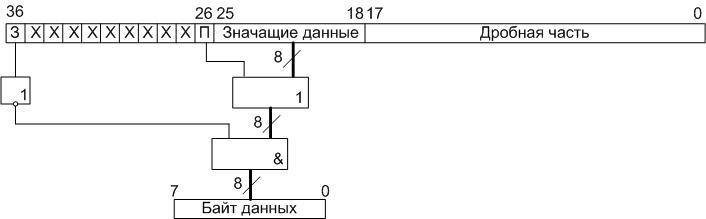
The calculation starts with the control device setting the starting address from the SRAM memory chip port, from which the pixel data is stored in the .bmp file, as mentioned above, the starting address value is 36h. The .bmp files at this address store the value of the blue color component of the lowest right pixel of the image. At address 37h - the value of the green color component, then red, then the blue component of the next pixel again goes to the bottom line of the image, etc. As you can see from the functional diagram, there is a register for each color component in the diagram. After loading from the memory of all three color components into their registers, from the next clock of the generator, the results of the calculations are written to the memory. So, the monochromatic red component “Cr” is recorded at the address of the blue component “B”, the monochromatic blue component “Cb” is recorded at the address of the green component “G”, and the brightness component “Y” is recorded at the address of the component “R”. As a result of this step, the same image in the YCbCr format will appear in place of the original image in SRAM in RGB format.
For the hardware implementation of calculations of luminance and monochromatic components, all fractional coefficients from the formulas were presented in the form of sixteen-bit words in a fixed-point format, where the upper eight bits contain the integer part, respectively, in the lower eight bits - the fractional one. For example, a factor of 0.257 in a fixed-point binary representation looks like this: 0000000001000001 or in hexadecimal form 0041h. The limited number of digits reduces the accuracy, so if the binary fractional number 0000000001000001 is converted to decimal, we get: 2 ^ (- 2) + 2 ^ (- 8) = 0.25 + 0.00390625 = 0.25390625. As you can see, the result differs from the value 0.257, and to increase the accuracy of the representation, it is necessary to increase the number of digits allocated to the fractional part. But I decided to limit myself, as was said above, to eight digits.
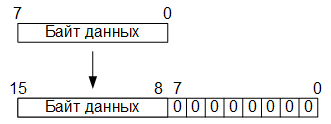
So, at the first stage of conversion, eight-bit values of the RGB color components are converted to sixteen-bit in a fixed-point format by adding eight least significant bits filled with zero bits:
At the second stage, operations of multiplication, addition and / or subtraction are performed. As a result of which thirty-two-digit data are obtained, where the sixteen senior digits contain the integer part, the sixteen junior digits contain the fractional part.
At the third stage, eight-bit data is formed from the received thirty-two-bit words by extracting eight bits immediately before the comma (if the serial number of the least significant bit is 0 and the oldest is 31, then these are bits 23 to 16):
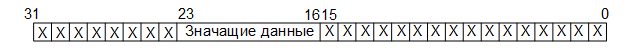
At the fourth stage, in accordance with the above formulas, offsets are added to the obtained eight-bit words (for the Y component - 16, for the Cb, Cr components - 128).
The conversion from YCbCr to RGB is carried out according to the following formulas:
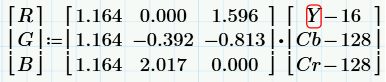
Here there is such a feature that the calculation results, in some cases, can acquire values greater than 255, which goes beyond one byte, or negative values, respectively, such situations need to be monitored.
So, if an overflow occurs, then the value of the final color component should be equal to 255, for this we just carry out the bitwise logical operation “OR” of the result with the overflow bit. And if the sign digit of the result is equal to one (that is, the value is less than zero), then the value of the final color component must be equal to 0, for this we carry out the bitwise logical operation “AND” of the result with the inverted value of the sign bit.
So, at the first stage of the operation of converting the YCbCr color space to RGB, read from the SRAM microcircuit, we translate the eight-digit values of the brightness and monochromatic components into an additional ten-digit code by adding the two most significant zero bits (sign bit and overflow sign). As a result, we get ten-digit words. Then, in accordance with the formulas, we subtract the bias values from these data (or add the negative bias values represented in the ten-digit additional code). Then, we translate the obtained result from the additional code into a straight line, saving the values of the most significant (signed) bit. We transform the remaining nine-bit words into eighteen-bit words with a fixed point by assigning the least nine bits with zero bits:
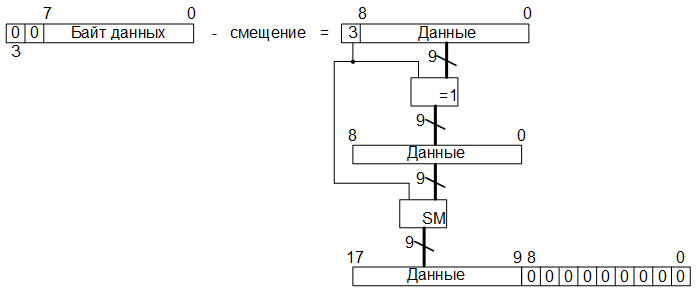
The fractional coefficients appearing in the formulas are also presented in the form of an eighteen-bit code with a fixed point, where 9 bits are allocated for the integer and fractional parts. As a result of the multiplication operations, we obtain thirty-six-digit values of the products, in which the 18 highest digits are the integer part, the 18 lower digits are fractional. Then we calculate the sign of the product by carrying out the logical operation “addition modulo 2”, the previously saved sign digit with the sign in front of the coefficient in the formula (if “-”, then “1”, if “+”, then “0”).
It is also necessary to determine if the result of the product is not zero, if the multiplication result is zero, then 0 should be written in the sign digit, regardless of the signs in front of the coefficients and the signs in front of the results obtained as a result of the displacement of the components read from memory. To do this, we apply the reduction operator (| product [35: 0]) to the product, which determines whether all bits as a result of multiplication are equal to zero (if so, then the result of this operator will be zero), after which we perform the logical “AND” operation the result obtained with the result of the operation "addition modulo 2" of significant digits.
After all this, we translate the results of the multiplication into an additional thirty-seven-digit code, where the sign is stored in the highest order, and we carry out the addition operations. After the addition operations, the results obtained in the additional code are translated into direct code, and we select eight bits immediately before the comma (if the number of the least significant bit is 0 and the most significant is 36, then these are bits 25 to 18). Next, we check if there was an overflow, for this, as mentioned above, we carry out the operation of a bitwise logical "OR" of the allocated eight bits with an overflow sign, which is stored in the 26th digit. And yet, we check to see if a negative result is obtained, for which we conduct a bitwise operation of a logical “AND” of an inverted sign bit with the same eight bits:
Obtained, as a result of calculations by three formulas, and converted eight-bit values are the values of the RGB color components.
I decided to test the device using a photo of Lena Soderberg measuring 256 by 256 pixels:

Everyone involved in image processing works with this photo, and I decided not to be an exception.
So, as a result of converting the original photo loaded via UART into the SRAM of the debug board from the RGB color space to the YCbCr space, the following image was obtained:

The image on the right is the original photo, the photo on the left is the result of the inverse transformation from the YCbCr space to the color space RGB as described above:

When comparing the original and the converted photo, you can see that the original photo is brighter than the processed one, this is due to loss of data that occurred during rounding (“rejection” of the fractional part), as well as loss of accuracy when representing fractional coefficients in binary form.
There is plenty of information on what a discrete cosine transform (hereinafter referred to as DCT) is on the Internet, so I will dwell on the theory briefly.
As was said in this publication, the essence of any basic transformation is to multiply the transformation matrix by the matrix of source data, after which the result is again multiplied by the transposed matrix of the same transformation. In the case of a discrete cosine transform, the coefficients of the transform matrix are calculated according to the following rule:
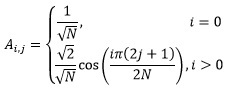
Where:
N - dimension of the matrix;
i, j are the indices of the elements of the matrix.
In our case, N = 8, i.e. the original image is divided into blocks of 8 by 8 pixels, while the values of the indices i and j vary in the range from 0 to 7.
As a result of applying this rule for N = 8, we obtain the following transformation matrix:
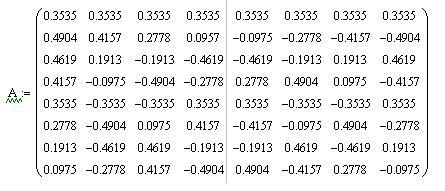
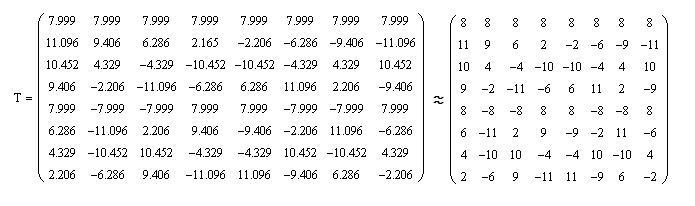
In order not to perform calculations with fractional numbers, multiply each element of the matrix is 8√8, and round off the obtained values of the matrix elements to integers, as a result of which we obtain the matrix T:
In this case, we will need the result of matrix multiplication, both in the case of a direct discrete cosine transform during coding, and in the case of the opposite during decoding, divide by 512. Given that 512 = 2 ^ (9), division is carried out by shifting the dividend to the right by 9 positions.
As a result of the direct discrete cosine transform, a matrix of the so-called DCT coefficients is obtained, in which the element located in the zero row and zero column is called the low-frequency coefficient and its value is always positive. The remaining elements of the DCT matrix are high-frequency coefficients, the values of which can be both positive and negative. Given this, and the fact that the elements of the resulting matrix should be eight-bit, for the low-frequency coefficient the range of values will be [0..255], and for high-frequency ones [-127..127]. In order to fit into these ranges, it is necessary to divide the results of the direct discrete cosine transform by 8, respectively, the results of the inverse - multiply by 8. As a result, for direct DCT we obtain the following formula:
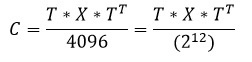
Where:
C is the matrix of coefficients of the discrete cosine transform;
T is the transformation matrix;
X is an 8 by 8 matrix of luminance or monochromatic components (depending on which, let's call it so, the Y, Cb or Cr component plane is encoded).
For the reverse DCT, we obtain the following formula:
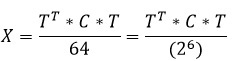
The coefficients of the matrix T in the eight-bit format are stored in the ROM memory located on the FPGA chip in the direct code, while the most significant bit contains the sign.
And so, at the first stage of the discrete cosine transform, from the SRAM memory to the operating unit performing direct DCT, 64 bytes of one of the components are read sequentially (the entire component plane Y is encoded first, then Cb and Cr), forming part of the image, as was written earlier size of 8 by 8 pixels (in this case, addresses for SRAM are generated in a special way): The
calculation operations in this block are carried out with twenty-bit data: 12 least significant bits - the values that will be lost when dividing by 4096 (2 ^ (12)), 8 s to defuse - meaningful portion and MSB - sign, total: 12 + 8 + 1 = 21:
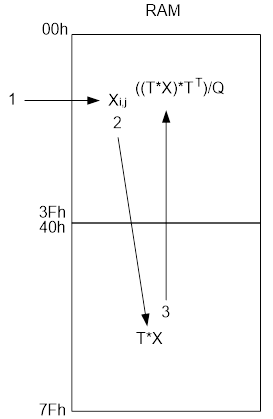
Based on this, during loading, the eight-bit data in the operating unit is converted into twenty-bit words represented in the additional code by assigning the highest thirteen bits filled with zero bits (the most significant bit is a character), after which the resulting word is stored in the RAM buffer located , also, on an FPGA chip, into the address space from 00h to 3Fh (Quartus II did not allow creating RAM memory with 128x21 organization, so I had to use memory with 128x32 organization).
At the second stage, after 64 twenty-bit words (block 8 by 8) are written into the RAM buffer memory, the matrix multiplication process is started. At the same time, an eight-bit string element of the transformation matrix is read from ROM memory, which is “expanded” into a twenty-bit word by writing the seventh (sign) bit of the value read from the ROM memory into the twentieth (sign) bit of the decompressed word. The remaining seven bits of the eight-bit value of the element of the transformation matrix are rewritten into the seven least significant bits of the decompressed word, bits with serial numbers 7-19 are filled with zeros:
Next, a twenty-bit column element is read from the RAM buffer memory, previously written there, after which its twenty least significant bits are multiplied with twenty bits of the expanded element of the transformation matrix. The sign of the product is calculated in the same way as when converting color spaces:
The work is translated into an additional code and stored on the stack, with a depth of 8 twenty-bit words. As soon as the stack is full (this means that the elements of the transformation matrix row are multiplied by the elements of the next column of the original matrix), all the stack values are summed and the result in additional code is written to the RAM buffer memory, in the address space from 40h to 7Fh. At the third stage, from the buffer memory RAM, from the address space 40h - 7Fh, the matrix elements, which is the result of the product of the transformation matrices and the original matrix, are read out line by line and converted to direct code. And from ROM memory, as before, they are also read, line by line, and the elements of the transformation matrix are expanded (contrary to the rule of matrix multiplication, here we multiply a row by a row, which means the transpose operation of the multiplier matrix). Then, as before, twenty-bit matrix elements are multiplied in the direct code, a signed digit is calculated, the product is transferred to an additional code and stored on the stack. As soon as the stack is filled with eight elements, they are summed, and the result from the additional code is translated into a straight line.
Next, a quantization operation is performed. Each element of the resulting matrix is divided into the so-called corresponding quantization coefficient, a table of which is stored in a separate ROM memory on the FPGA chip. The values of the quantization coefficients were calculated by the following formula:
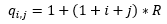
Where:
R is the compression coefficient, or the coefficient characterizing the loss of quality of the restored image in relation to the original;
i, j are the indices of the calculated element of the quantization matrix, varying from 0 to 7.
It must also be said that for all component planes Y, Cb, Cr, the codec uses one quantization matrix calculated for R = 2 (I did not bother making each table its own quantization coefficient table).
In order not to implement the divider in hardware, I replaced the division operation during quantization with the multiplication operation as follows:
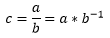
Where:
a - quantized coefficient, element of the effective matrix of the base transformation;
b is the corresponding coefficient of the quantization matrix calculated according to the previously given formula;
c is the result of quantization.
Accordingly, the results of raising to the power of -1 (or 1 / b), presented in a fixed-point format, are recorded in the ROM memory, while only 8 bits of the fractional part are stored in the memory, since the integer part is always equal to 0.
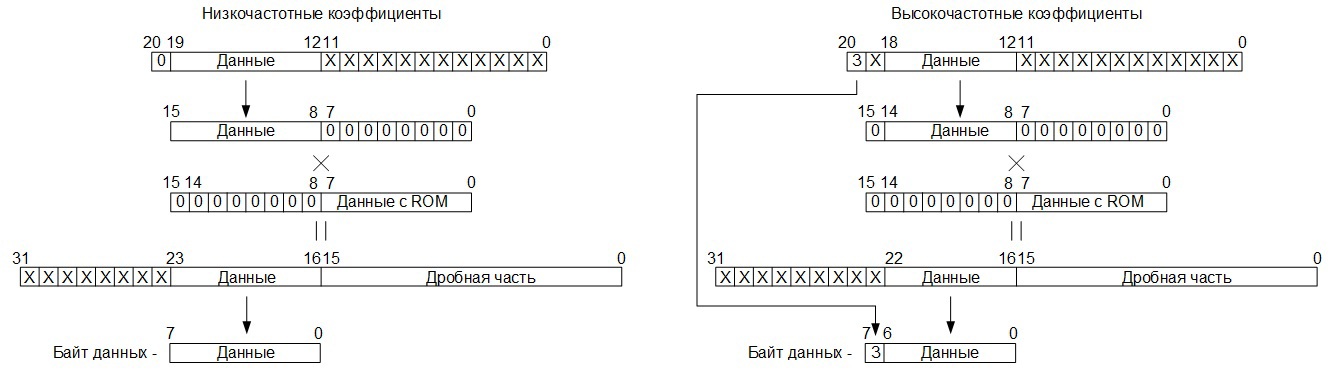
The quantization process in the codec is implemented as follows: as soon as the next twenty-bit element of the resulting linear transformation matrix is calculated and transferred from the additional code to the straight line, it is determined whether this element is a low-frequency coefficient and, if so, bits 19 through 12 are written into the eight high order bits of the intermediate sixteen-bit register, the 8 least significant bits of this register, in this case, are filled with zeros (bits 11 to 0 of the original twenty-bit word are discarded, so about there is a division operation by 4096).
If the element is a high-frequency coefficient, then 0 is written in the most senior bit of the intermediate register, bits from 18 to 12 of twenty-bit words are written in the next seven bits, and the 8 least significant bits of the intermediate register are also filled with zeros. The outputs from this intermediate register are connected to one of the input ports of the 16x16 multiplier, the values from the ROM memory, where the fractional parts of the quantization coefficients raised to the power of -1 are stored, are sent to the other port of this multiplier. Moreover, zero values are supplied to the 8 senior pins of the port, and values read from the ROM memory to the 8 lower pins.
Далее, с тридцатидвухразрядного выходного порта умножителя считывается результат квантования, в котом 16 младших разрядов – дробная часть, которая отбрасывается, а 8 разрядов, стоящих непосредственно перед фиксированной запятой, это значащая часть (я думаю и так понятно, что результат квантования – это дробное число, представленное в формате с фиксированной точкой). Причём, в случае с низкочастотными коэффициентами, значащей частью являются не 8, а 7 разрядов, стоящих непосредственно перед запятой, в восьмой разряд здесь переписывается знак, полученный ещё на этапе базового преобразования, находящийся в самом старшем разряде:
Ну и далее, сформированные восьмиразрядные значения записываются в буферную память RAM в адресное пространство 00h – 3Fh:
Ready data from the buffer memory is read in accordance with the zigzag scan algorithm (what zigzag scanning can be read here ) and go to the stage of encoding the lengths of the series.
Decoding goes in reverse order. And here we are already operating with fifteen-bit data: the 6 least significant bits - the bits that are lost when dividing by 64, 8 bits - a significant part, 1 bit - a sign. Total: 6 + 8 + 1 = 15:
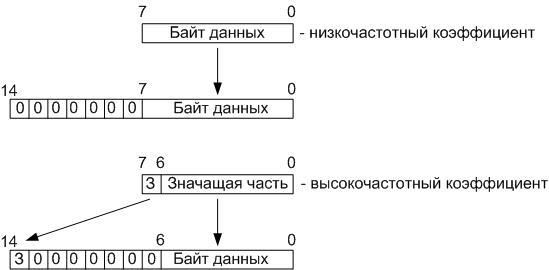
At the first stage, received in the operating unit, performing the inverse discrete cosine transformation, an eight-bit word is expanded to a fifteen-bit. To do this, first check to see if the byte arrived is a low-frequency coefficient, and if so, then all 8 bits are overwritten into the 8 least significant bits of the fifteen-bit word. And if a high-frequency coefficient has been received, then the 7 least significant bits of the byte received are overwritten into the seven least significant bits of the fifteen-bit word, and the highest digit containing the character is written to the highest digit of the fifteen-bit word.
Then, the data expanded to 15 bits is written to the RAM buffer memory in the address space 00h - 3Fh in accordance with the zigzag scanning algorithm. After the matrix of quantized DCT coefficients of size 8 by 8 is formed in the RAM memory, the process of inverse discrete cosine transformation begins, as described above. In this case, every fifteen-digit word read with RAM, first goes through the restoration procedure (the inverse to quantization procedure) by multiplying by the corresponding quantization coefficient stored in the ROM memory.
Here, the fourteen-bit word is multiplied by an eight-bit quantization coefficient, which is an integer (these are the values that were raised to the power of -1 when compressed). Next, matrix multiplication is carried out as described above. After that, the low-order bits are discarded from the resulting fifteen-digit values (division by 64) and the sign digit is checked, and if its value is 0, then the next eight bits contain the resulting value of the decoded component Y, Cb, or Cr (depending on which component plane decoded). And if the sign digit is 1, then the next 8 digits are simply reset (i.e., rounded to 0, because the result of the inverse DCT cannot be negative).
The obtained eight-bit results of the inverse DCT are written into the RAM buffer memory, thus forming an 8 by 8 image block. After the block is formed, each of its elements is written to the external SRAM memory at the corresponding address, forming, in turn, the final image in space YCbCr.
And now, finally, we got to the point for which everything was up to. The Walsh transformation is a type of basic transformation, the transformation matrix of which is as follows:
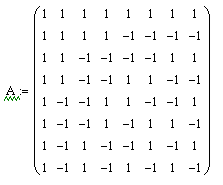
Information about where this matrix comes from, how it is derived and how it is formed can also be found on the Internet or in textbooks on the theory of circuits and signals. We will not dwell on this.
So, as mentioned above, the basic transformation is reduced to multiplying the transformation matrix by the matrix of source data, after which the result is again multiplied by the transposed matrix of the same transformation. The values of all the elements of the Walsh transform matrix are either 1 or -1; accordingly, only the operations of adding data presented in the additional code will be required to perform hardware operations. If we paint the process of multiplying the Walsh matrix by the original matrix of the image block 8 by 8, we get the following expressions for each row element of the intermediate matrix:
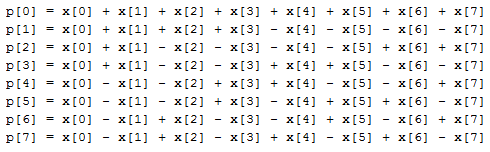
Where:
p [0..7] - the next row of the intermediate matrix;
x [0..7] is the next row of the original matrix, which is an 8 by 8 image block.
And further, if we paint the process of multiplying the intermediate matrix by the transposed Walsh matrix, we get the following expressions for each column element of the resulting matrix:

Where:
y [0..7] is the next column of the resulting matrix;
p [0..7] is the next column of the intermediate matrix.
As in the case of DCT, the upper left element of the resulting matrix will be a low-frequency coefficient, the value of which is always greater than 0, and the remaining 63 elements will be high-frequency coefficients, the values of which can be either less than or greater than 0 (as well as with DCT) .
Hardware, the Walsh transform block is a group of adders connected in a certain way, the inputs of which are first fed into the rows of the original matrix, the results are stored in a buffer, and then the columns of the previously obtained matrix are fed from the buffer to the inputs of the same group of adders. It should also be taken into account that with the direct Walsh transformation, the values of the elements of the resulting matrix can go beyond 255, so they will need to be divided by 64 or shifted by 6 digits to the right.
The inverse Walsh transformation is carried out in exactly the same way with the only exception that the elements of the resulting matrix, which will be an 8 by 8 image block, need not be divided by anything, the values are already normalized.
So, in the direct Walsh transform block, the incoming eight-bit component values, by analogy with the DCT block, are expanded into fifteen-bit ones (6 bits - bits that will be lost when divided by 64, 8 bits - significant bits, 1 bit - sign) and are written to the buffer memory RAM As soon as an 8 by 8 matrix is formed in the buffer, the elements of the original matrix are read out from the buffer, converted, and written to the addresses of the same line from which they were read. This makes it possible to use RAM memory with 64x15 organization (in the case of DCT, a buffer with 128x21 organization was required), but Quartus II allowed creating a RAM memory block with 64x16 organization only, one bit remained unused (although in the case of DCT 11 bits were not used).
Then, the columns of the matrix obtained in the previous step are already read from the buffer, converted, and the result of this conversion is transferred from the additional code to the direct one, after which the quantization operation is carried out exactly as in the case of direct DCT, the result of which is written to the RAM buffer memory, from where then read in accordance with the zigzag scanning algorithm. The inverse Walsh transform is carried out similarly to the direct one, the incoming data is then written into the RAM buffer in the zigzag scanning algorithm, and when read for the direct Walsh transform, they are multiplied by the corresponding quantization coefficients.
Below, in comparative form, the results of the operation of the direct Walsh transform and direct discrete cosine transform blocks are presented:

At the top left is a photograph on which we are training, which was first translated, say, inside our debug board, from the RGB color space to the YCbCr space, then each component plane was divided into 8 by 8 blocks and converted according to the direct Walsh transform rule. At the top right is the same photograph converted according to the direct DCT rule. Bottom left is the result of the Walsh transform subjected to the quantization operation, respectively, bottom right is the subjected to the quantization operation, the result of direct DCT read from the debug board.
The series length encoding algorithm is also called, in a different way, a compression algorithm that uses run length exclusion (RLE). This algorithm is based on the principle of determining groups of identical, consecutive characters (bytes with the same values), and replacing them with a specific structure containing the number of repetitions and a code of repeating characters, i.e. <number of retries> <repeated character (byte)>. Obviously, the maximum number of identical characters (data bytes) that can be encoded with such a structure depends on the length of the number of retries code.
For implementation, it was decided to choose an algorithm that is implemented in the graphic .pcx format. In this RLE algorithm, the peculiarity is that the number of repetitions is encoded by the counter byte, in which the upper two bits contain units, and the lower six contain the number of repetitions. Accordingly, the values of bytes that are not repeated in a row and whose values are less than C0h are transferred to the compressed data stream without change. And byte values that are not repeated in succession are large C0h, (two units in the upper digits), when written to the output stream, in any case, are preceded by a counter byte, and, since there is only one such symbol in the stream, the byte counter takes on the value C1h. It should also be taken into account that the maximum number of retries that can be encoded in six allocated bits is 63 = 3Fh, therefore, after each entrapment of the retry counter, it is necessary to check if its value is 63, and if so, into the output stream, first,
Например, на выходе блока базового преобразования (будь то блок прямого ДКП или быстрого преобразования Уолша) имеем следующий поток данных, выдаваемых с буферной памяти RAM в соответствии с алгоритмом зигзаг-сканирования: ECh, C2h, 03h, 0Ah, 0Ah, D1h, D1h, 01h, 01h, 01h, 00h, 00h, 00h, 00h, 00h, 02h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h. Тогда, после кодирования данного потока, алгоритмом RLE, получим следующий поток данных: C1h, ECh, C1h, C2h, 03h, C2h, 0Ah, C2h, D1h, C3h, 01h, C5h, 00h, 02h, F0h, 00h.
In total, in our case, from a string of length 64 bytes, after compression, a string of length 16 bytes was obtained, in which the largest number of repetitions belongs to zero bytes. These zero bytes are rounded to zero after quantization, high-frequency coefficients, respectively, if quantization is not carried out, the number of consecutive zero bytes will be significantly lower, which will give a lower compression ratio, but will save image quality.
Hardware-wise, this algorithm is implemented quite simply both during compression and during unpacking.
When unpacking after receiving the next byte, we check its most significant two bits, and if their values are equal to one, then load the least six bytes into the counter, read the next byte without checking its most significant bits, put it into the output stream, decrementing, at the same time, the counter until it is zeroed, after which we read the next byte from the stream, and if the values of the highest bits of the counter are different from two units, then we rewrite this byte into the output stream without changes.
In the codec, the RLE encoding algorithm is executed by the control device while reading data bytes from the basic transform unit during compression, the RLE decoding algorithm is executed before the data is loaded into the basic transform unit during unpacking (I think this is clear).
More than one article published on this site has been devoted to the Huffman algorithm; therefore, as before, I will not dwell on theory. I can only say that, by analogy with the JPEG algorithm, in the device described here, I implemented the Huffman algorithm with pre-computed, fixed tables.
The difference from the JPEG algorithm is that only the code lengths are stored in the tables in the JPEG, and not the codes themselves, in the same device, sixteen-bit Huffman codes are stored separately in one ROM memory, and the number of significant bits in each of the ROMs is stored sixteen-digit codes, starting with the oldest. Also, in JPEG, different tables are used for low-frequency and high-frequency coefficients, and instead of the low-frequency coefficient values themselves, their differences are encoded. In my device, I didn’t complicate things this way (maybe in vain) and, in the device I developed, all the coefficients are encoded in a single stream and a single table.
The encoding is carried out as follows: the address inputs of the ROM memory blocks are encoded bytes (a data stream encoded by the RLE algorithm), while the number of bits whose value was read from the output of another is read from the output of the ROM memory block, where the Huffman codes are stored ROM memory block. Huffman codes and their lengths are stored at those addresses whose values correspond to the values of the encoded bytes.
Further, from the read bit stream, bytes are formed and written into memory. For example, when encoding one byte, 4 bits were read from the ROM containing the Huffman code, while encoding the second byte in the stream - 11 bits, the third - 3, and the fourth - 4. Total, we get 4 + 11 + 3 + 4 = 22, 22 bits are divided by 8, we get 2 bytes and 6 bits, to which we append, in the least significant bits, two zero bits (the last byte in the stream is encoded) and we get 3 equivalent bytes, which are written to external memory, i.e. . out of four bytes at the input, three were received at the output.
The Huffman decoder is implemented in the form of a truth table, in the AHDL language (in this language, a special “TABLE” operator is provided for this, although it could be done in Verilog using the “case” operator, as you like), which has one a sixteen-bit input port for the Huffman code and one five-bit input port for the length of this code.
Decoding is carried out as follows: byte is read from the SRAM external memory, which is bitwise loaded into the sixteen-bit register, starting from the high-order bit, the outputs of which are connected to the sixteen-bit input port of the Huffman decoder (the same table), after loading the next bit, the counter connected to the other is incremented Huffman decoder port.
After loading the next bit, the signal is checked, meaning that the input combination of the Huffman code and the length of the code, the output byte is found, and if the value of this signal is a logical unit, then the byte is read from the output port of the Huffman decoder, which goes to RLE decoding. In this case, the sixteen-bit register is reset, and the bits remaining in the byte are loaded into it again from the high order, if the bits in the byte read from the external memory are expired, then a new byte is read, etc.
At the first stage, an encoder was compiled and flashed into the FPGA, which performs compression based on the fast Walsh transform, with quantization of the coefficients. As a result, uploaded by UART to the device, our test image of 256 by 256 pixels in size with a memory capacity of 192 Kbytes was converted (compressed) into a file with a memory capacity of 8.1 Kbytes.
At the second stage, an encoder was compiled and flashed into the FPGA, which performs compression based on the fast Walsh transform, but without quantization of the coefficients. As a result, the same image was converted (compressed) to a file with a storage capacity of 43.8 KB.
At the third stage, an encoder was compiled and flashed into the FPGA, which performs compression based on a discrete cosine transform, with quantization of the coefficients. As a result, uploaded by UART to the device, our test image of 256 by 256 pixels in size with a memory capacity of 192 Kbytes was converted (compressed) into a file with a memory capacity of 8.17 Kbytes.
At the fourth stage, an encoder was compiled and flashed into the FPGA, which performs compression based on a discrete cosine transform, without quantizing the coefficients. As a result, the same image was converted (compressed) to a file with a storage capacity of 35.9 KB.
Below are the results of unpacking, developed by the device, previously compressed images.
На рисунке, представленном ниже, в центре показано исходное изображение, слева – изображение, сжатое с квантованием коэффициентов, при помощи быстрого преобразования Уолша, справа – изображение, сжатое с квантованием коэффициентов, при помощи дискретного косинусного преобразования:

Разницу в базовых преобразованиях отчётливо при увеличении одинаковых участков изображений. Так, преобразование Уолша даёт более контрастные границы на участках переходов, в свою очередь, ДКП делает переходы на границах более плавными.
Ниже представлены результаты распаковки изображений, которые сжимались без квантования коэффициентов. Также как и в предыдущем случае, в центре — исходное изображение, слева – изображение, сжатое при помощи быстрого преобразования Уолша, справа – при помощи ДКП:

At first glance, there are no special losses in quality, but if you enlarge the image, you can see the borders of 8 by 8 blocks, which, in the case of the Walsh transformation, also have more contrasting borders, and in the case of DCT, they are smoother. In general, a number of works have been written regarding issues of assessing image quality, and I don’t really want to do this here.
And so, below is a table containing the results of determining the compression characteristics obtained on the developed device, an image measuring 256 by 256 pixels in .bmp format with a memory footprint (L) of 192 KB. The size of the original image is calculated as follows: 256 × 256 = 65536 pixels, each byte has three bytes (1 byte is the red component, 1 byte is the green component, 1 byte is the blue component), we get 65536 × 3 = 196608 bytes, plus 53 bytes - the header, total we get 196661 bytes or 196661/1024 ≈ 192 KB with "pennies":
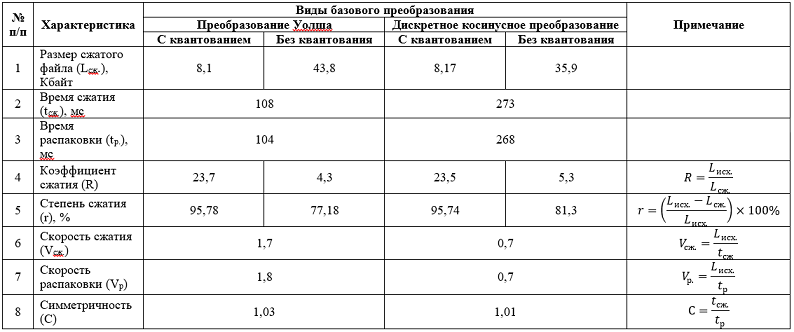
It can be seen from the table that both methods of basic conversion in hardware implementation give practically the same results, with the exception of time and speed of compression / decompression. Here, the Walsh transform wins over the special case of the Fourier transform - DCT. 1 - 0 in favor of the Walsh transformation.
If we compare both types of conversions in terms of the cost of FPGA hardware resources, we get the following:
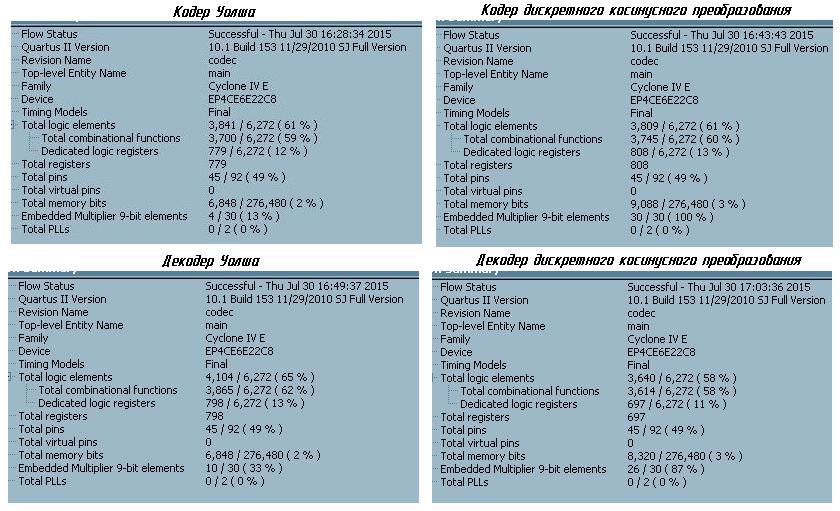
From the screenshots shown, it is clear that the FPGA hardware resources, both conversions consume the same, except for the use of built-in multipliers. Here, a special case of the Fourier transform again lost to the Walsh transform. Total: 2 - 0 in favor of the Walsh transformation.
In principle, we can conclude that, from the point of view of hardware implementation, it is better to use, as a basic transformation, the Walsh transformation.
Well, in the very conclusion, I want to note that this hardware codec for image compression / decompression was developed, let's say, thoughtlessly and thoughtlessly. This explains the unsatisfactory (at least it seemed to me) values of the temporal characteristics of compression / decompression. Looking through the project again and again, I always find optimization opportunities and options for reducing the image processing time, while increasing the size of the processed (compressed / unpacked) image. As a result, it will be possible to achieve a compression / decompression speed of 24 images per second, which will allow processing video streams.
Well, that’s all. Thanks for attention!
First, I want to thank the author of the articles “Decoding JPEG for Dummies” and “Inventing JPEG” , which helped me a lot in writing this publication. When I started studying the problems of lossy image compression algorithms, I was constantly tormented by the question regarding the JPEG algorithm: “Why is the role of the basic transformation in the JPEG algorithm assigned to the particular case of the Fourier transform?” Herethe author gives an answer to this question, but I decided to approach it not from the point of view of theory, mathematical models or software implementation, but from the point of view of circuitry.
The JPEG image compression algorithm is a digital signal processing algorithm that, as a rule, is implemented in hardware either on digital signal processors or on programmable logic integrated circuits. In my case, the choice for the digital signal processor to work would mean coming to what I was trying to get away from - a software implementation, so it was decided to focus on programmable logic.
In one of the online stores I purchased a fairly simple debug board, which contains Altera FPGA Cyclone 4 -EP4CE6E22 FPGAs and 512Kx8 SRAM. Since the FPGA was Altera, it was decided to use Quartus II Web Edition for development. The development of individual functional blocks of the hardware codec was carried out in the Verilog language , and the assembly into a single circuit was carried out in the graphical editor of the Quartus II Web Edition environment.
To communicate with a personal computer (receiving commands, receiving / transmitting processed data), in Verilog language I wrote a simple asynchronous UART transceiver . To connect to the COM-port ( RS-232 ) of the computer, based on the MAX3232WE chip and from what was at hand, the level converter was hastily soldered. In the end, here's what happened:

To send commands from a personal computer, as well as transmit / receive data, we used the trial version of the ADVANCED SERIAL PORT MONITOR program , which allows you to generate not only individual data byte packets, but also generate data streams from file contents, as well as write received data streams to a file, which allowed you to send and receive files. I don’t use and control any protocols and checksums for receiving / transmitting data via UART (I was just too lazy to foresee and implement all this), during the connection for receiving / transmitting I used what is called “raw data”.
All arithmetic operations associated with fractional numbers in the codec are carried out in a fixed-point format., addition and subtraction operations are carried out in an additional code , in principle, this is already understandable. How bit depth of the processed data was determined will be described below.
The compression operation is performed on the original images presented in .bmp format with a color depth of 24 bits per pixel (8 bits for each of the color components).
The memory on the debug board was organized as follows: addresses 00000h through 3FFFFh (in hexadecimal notation) are allocated for storing the source data (a picture in .bmp format for compression, or encoded data for decompression), total 256 KB, the remaining 256 KB is the space for recording the data received as a result of compression or decompression, these are addresses from 40000h to 7FFFFh. I think it is obvious that the maximum size of compressed images is limited by the amount allocated for storing data, memory.
The device’s operation algorithm is as follows: immediately after power is supplied, the codec expects a UART data stream, any received data is interpreted here as the source file for processing, if the pause between bytes is 10 ms, then this is interpreted as the end of the file, and the one after the pause bytes received via UART are perceived by the device as a command. Commands are specific byte values. For example, after receiving the file after 10 ms, received in the codec via UART, the value of the AAh byte is interpreted by the device as a command by which the data from the memory microcircuit is transmitted via UART to the computer, starting from the address 40000h and until the value of the address at which the processing of recorded data ended , i.e. The results of compression / decompression are transferred to the computer. The value EEh is interpreted as an image compression / decompression command,
As for the structure of the file with the squeezed image, I decided not to bother, and, unlike the JPEG algorithm, the algorithm I implement is pretty narrow-minded and is not designed for all occasions, so the data obtained as a result of compression is unified the stream is written to the allocated memory area. The only thing that needs to be noted here, in order not to implement the header generator of the .bmp file (it was also laziness), during compression it is simply completely rewritten to the initial (from address 40000h) memory area allocated for the final data, and then, starting from the offset from which the pixel data is stored in the original .bmp file, compressed data is recorded. This offset is stored in the header of the .bmp file at 0Ah relative to its beginning, and is usually 36h. When unpacking,
So, image compression with JPEG-like algorithms is carried out in the following sequence:
- color space conversion from RGB to YCbCr or YUV ;
- color subsampling ;
- basic transformation;
- quantization of the coefficients obtained after the basic transformation;
- Zigzag scan
- coding of lengths of series ;
- Huffman compression .
Unpacking is in the reverse order.
Of all the above steps, in the codec, I did not implement sub-sampling, since I considered it superfluous (maybe I'm wrong).
Based on the above sequence of actions, I developed the following codec functional diagram:

The codec operation process is controlled by a control device, which is a finite state machine, encoding / decoding of series lengths, as well as the generation of final data from Huffman codes during compression and the formation of Huffman codes from the SRAM data received during unpacking. The control device also generates control signals for other operating units.
Under the main scheme, the operating unit schemes are presented, changing which in the main scheme, I changed the operating modes of the device. There was an attempt to assemble everything into a single device and set the codec's operating modes, as well as basic conversion methods using UART commands, but the FPGA logical capacity was not enough. Therefore, the operating modes of the device are changed by changing the corresponding operating units and the task of certain parameters in the control device (including the size of the compressed / unpacked image), after which the changed project is compiled and flashed into the FPGA.
Color space conversion
On the Internet you can find a lot of different information on the conversion of color spaces, so immediately start with a description of the hardware implementation.
The color space conversion unit is a combinational logic, due to which the color components are converted in one clock cycle of the generator. The conversion of the RGB color space to YCbCr is carried out according to the following formulas:

The calculation starts with the control device setting the starting address from the SRAM memory chip port, from which the pixel data is stored in the .bmp file, as mentioned above, the starting address value is 36h. The .bmp files at this address store the value of the blue color component of the lowest right pixel of the image. At address 37h - the value of the green color component, then red, then the blue component of the next pixel again goes to the bottom line of the image, etc. As you can see from the functional diagram, there is a register for each color component in the diagram. After loading from the memory of all three color components into their registers, from the next clock of the generator, the results of the calculations are written to the memory. So, the monochromatic red component “Cr” is recorded at the address of the blue component “B”, the monochromatic blue component “Cb” is recorded at the address of the green component “G”, and the brightness component “Y” is recorded at the address of the component “R”. As a result of this step, the same image in the YCbCr format will appear in place of the original image in SRAM in RGB format.
For the hardware implementation of calculations of luminance and monochromatic components, all fractional coefficients from the formulas were presented in the form of sixteen-bit words in a fixed-point format, where the upper eight bits contain the integer part, respectively, in the lower eight bits - the fractional one. For example, a factor of 0.257 in a fixed-point binary representation looks like this: 0000000001000001 or in hexadecimal form 0041h. The limited number of digits reduces the accuracy, so if the binary fractional number 0000000001000001 is converted to decimal, we get: 2 ^ (- 2) + 2 ^ (- 8) = 0.25 + 0.00390625 = 0.25390625. As you can see, the result differs from the value 0.257, and to increase the accuracy of the representation, it is necessary to increase the number of digits allocated to the fractional part. But I decided to limit myself, as was said above, to eight digits.
So, at the first stage of conversion, eight-bit values of the RGB color components are converted to sixteen-bit in a fixed-point format by adding eight least significant bits filled with zero bits:

At the second stage, operations of multiplication, addition and / or subtraction are performed. As a result of which thirty-two-digit data are obtained, where the sixteen senior digits contain the integer part, the sixteen junior digits contain the fractional part.
At the third stage, eight-bit data is formed from the received thirty-two-bit words by extracting eight bits immediately before the comma (if the serial number of the least significant bit is 0 and the oldest is 31, then these are bits 23 to 16):
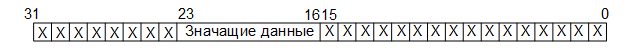
At the fourth stage, in accordance with the above formulas, offsets are added to the obtained eight-bit words (for the Y component - 16, for the Cb, Cr components - 128).
The conversion from YCbCr to RGB is carried out according to the following formulas:
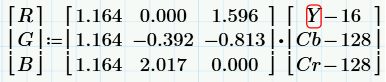
Here there is such a feature that the calculation results, in some cases, can acquire values greater than 255, which goes beyond one byte, or negative values, respectively, such situations need to be monitored.
So, if an overflow occurs, then the value of the final color component should be equal to 255, for this we just carry out the bitwise logical operation “OR” of the result with the overflow bit. And if the sign digit of the result is equal to one (that is, the value is less than zero), then the value of the final color component must be equal to 0, for this we carry out the bitwise logical operation “AND” of the result with the inverted value of the sign bit.
So, at the first stage of the operation of converting the YCbCr color space to RGB, read from the SRAM microcircuit, we translate the eight-digit values of the brightness and monochromatic components into an additional ten-digit code by adding the two most significant zero bits (sign bit and overflow sign). As a result, we get ten-digit words. Then, in accordance with the formulas, we subtract the bias values from these data (or add the negative bias values represented in the ten-digit additional code). Then, we translate the obtained result from the additional code into a straight line, saving the values of the most significant (signed) bit. We transform the remaining nine-bit words into eighteen-bit words with a fixed point by assigning the least nine bits with zero bits:

The fractional coefficients appearing in the formulas are also presented in the form of an eighteen-bit code with a fixed point, where 9 bits are allocated for the integer and fractional parts. As a result of the multiplication operations, we obtain thirty-six-digit values of the products, in which the 18 highest digits are the integer part, the 18 lower digits are fractional. Then we calculate the sign of the product by carrying out the logical operation “addition modulo 2”, the previously saved sign digit with the sign in front of the coefficient in the formula (if “-”, then “1”, if “+”, then “0”).
It is also necessary to determine if the result of the product is not zero, if the multiplication result is zero, then 0 should be written in the sign digit, regardless of the signs in front of the coefficients and the signs in front of the results obtained as a result of the displacement of the components read from memory. To do this, we apply the reduction operator (| product [35: 0]) to the product, which determines whether all bits as a result of multiplication are equal to zero (if so, then the result of this operator will be zero), after which we perform the logical “AND” operation the result obtained with the result of the operation "addition modulo 2" of significant digits.
After all this, we translate the results of the multiplication into an additional thirty-seven-digit code, where the sign is stored in the highest order, and we carry out the addition operations. After the addition operations, the results obtained in the additional code are translated into direct code, and we select eight bits immediately before the comma (if the number of the least significant bit is 0 and the most significant is 36, then these are bits 25 to 18). Next, we check if there was an overflow, for this, as mentioned above, we carry out the operation of a bitwise logical "OR" of the allocated eight bits with an overflow sign, which is stored in the 26th digit. And yet, we check to see if a negative result is obtained, for which we conduct a bitwise operation of a logical “AND” of an inverted sign bit with the same eight bits:
Obtained, as a result of calculations by three formulas, and converted eight-bit values are the values of the RGB color components.
I decided to test the device using a photo of Lena Soderberg measuring 256 by 256 pixels:

Everyone involved in image processing works with this photo, and I decided not to be an exception.
So, as a result of converting the original photo loaded via UART into the SRAM of the debug board from the RGB color space to the YCbCr space, the following image was obtained:

The image on the right is the original photo, the photo on the left is the result of the inverse transformation from the YCbCr space to the color space RGB as described above:

When comparing the original and the converted photo, you can see that the original photo is brighter than the processed one, this is due to loss of data that occurred during rounding (“rejection” of the fractional part), as well as loss of accuracy when representing fractional coefficients in binary form.
Basic transformations and quantization of coefficients
Discrete cosine transform
There is plenty of information on what a discrete cosine transform (hereinafter referred to as DCT) is on the Internet, so I will dwell on the theory briefly.
As was said in this publication, the essence of any basic transformation is to multiply the transformation matrix by the matrix of source data, after which the result is again multiplied by the transposed matrix of the same transformation. In the case of a discrete cosine transform, the coefficients of the transform matrix are calculated according to the following rule:
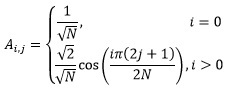
Where:
N - dimension of the matrix;
i, j are the indices of the elements of the matrix.
In our case, N = 8, i.e. the original image is divided into blocks of 8 by 8 pixels, while the values of the indices i and j vary in the range from 0 to 7.
As a result of applying this rule for N = 8, we obtain the following transformation matrix:
In order not to perform calculations with fractional numbers, multiply each element of the matrix is 8√8, and round off the obtained values of the matrix elements to integers, as a result of which we obtain the matrix T:
In this case, we will need the result of matrix multiplication, both in the case of a direct discrete cosine transform during coding, and in the case of the opposite during decoding, divide by 512. Given that 512 = 2 ^ (9), division is carried out by shifting the dividend to the right by 9 positions.
As a result of the direct discrete cosine transform, a matrix of the so-called DCT coefficients is obtained, in which the element located in the zero row and zero column is called the low-frequency coefficient and its value is always positive. The remaining elements of the DCT matrix are high-frequency coefficients, the values of which can be both positive and negative. Given this, and the fact that the elements of the resulting matrix should be eight-bit, for the low-frequency coefficient the range of values will be [0..255], and for high-frequency ones [-127..127]. In order to fit into these ranges, it is necessary to divide the results of the direct discrete cosine transform by 8, respectively, the results of the inverse - multiply by 8. As a result, for direct DCT we obtain the following formula:
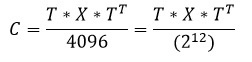
Where:
C is the matrix of coefficients of the discrete cosine transform;
T is the transformation matrix;
X is an 8 by 8 matrix of luminance or monochromatic components (depending on which, let's call it so, the Y, Cb or Cr component plane is encoded).
For the reverse DCT, we obtain the following formula:
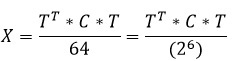
The coefficients of the matrix T in the eight-bit format are stored in the ROM memory located on the FPGA chip in the direct code, while the most significant bit contains the sign.
And so, at the first stage of the discrete cosine transform, from the SRAM memory to the operating unit performing direct DCT, 64 bytes of one of the components are read sequentially (the entire component plane Y is encoded first, then Cb and Cr), forming part of the image, as was written earlier size of 8 by 8 pixels (in this case, addresses for SRAM are generated in a special way): The

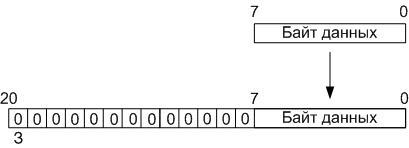
calculation operations in this block are carried out with twenty-bit data: 12 least significant bits - the values that will be lost when dividing by 4096 (2 ^ (12)), 8 s to defuse - meaningful portion and MSB - sign, total: 12 + 8 + 1 = 21:
Based on this, during loading, the eight-bit data in the operating unit is converted into twenty-bit words represented in the additional code by assigning the highest thirteen bits filled with zero bits (the most significant bit is a character), after which the resulting word is stored in the RAM buffer located , also, on an FPGA chip, into the address space from 00h to 3Fh (Quartus II did not allow creating RAM memory with 128x21 organization, so I had to use memory with 128x32 organization).
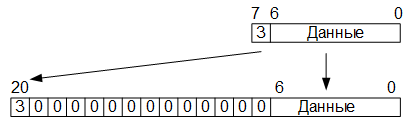
At the second stage, after 64 twenty-bit words (block 8 by 8) are written into the RAM buffer memory, the matrix multiplication process is started. At the same time, an eight-bit string element of the transformation matrix is read from ROM memory, which is “expanded” into a twenty-bit word by writing the seventh (sign) bit of the value read from the ROM memory into the twentieth (sign) bit of the decompressed word. The remaining seven bits of the eight-bit value of the element of the transformation matrix are rewritten into the seven least significant bits of the decompressed word, bits with serial numbers 7-19 are filled with zeros:

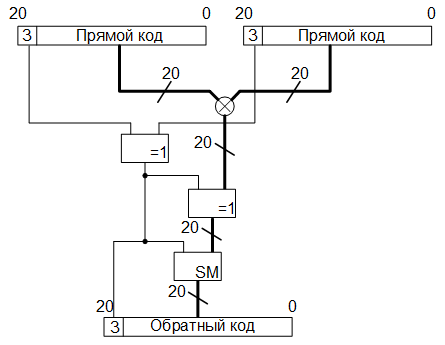
Next, a twenty-bit column element is read from the RAM buffer memory, previously written there, after which its twenty least significant bits are multiplied with twenty bits of the expanded element of the transformation matrix. The sign of the product is calculated in the same way as when converting color spaces:

The work is translated into an additional code and stored on the stack, with a depth of 8 twenty-bit words. As soon as the stack is full (this means that the elements of the transformation matrix row are multiplied by the elements of the next column of the original matrix), all the stack values are summed and the result in additional code is written to the RAM buffer memory, in the address space from 40h to 7Fh. At the third stage, from the buffer memory RAM, from the address space 40h - 7Fh, the matrix elements, which is the result of the product of the transformation matrices and the original matrix, are read out line by line and converted to direct code. And from ROM memory, as before, they are also read, line by line, and the elements of the transformation matrix are expanded (contrary to the rule of matrix multiplication, here we multiply a row by a row, which means the transpose operation of the multiplier matrix). Then, as before, twenty-bit matrix elements are multiplied in the direct code, a signed digit is calculated, the product is transferred to an additional code and stored on the stack. As soon as the stack is filled with eight elements, they are summed, and the result from the additional code is translated into a straight line.
Next, a quantization operation is performed. Each element of the resulting matrix is divided into the so-called corresponding quantization coefficient, a table of which is stored in a separate ROM memory on the FPGA chip. The values of the quantization coefficients were calculated by the following formula:
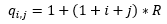
Where:
R is the compression coefficient, or the coefficient characterizing the loss of quality of the restored image in relation to the original;
i, j are the indices of the calculated element of the quantization matrix, varying from 0 to 7.
It must also be said that for all component planes Y, Cb, Cr, the codec uses one quantization matrix calculated for R = 2 (I did not bother making each table its own quantization coefficient table).
In order not to implement the divider in hardware, I replaced the division operation during quantization with the multiplication operation as follows:
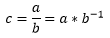
Where:
a - quantized coefficient, element of the effective matrix of the base transformation;
b is the corresponding coefficient of the quantization matrix calculated according to the previously given formula;
c is the result of quantization.
Accordingly, the results of raising to the power of -1 (or 1 / b), presented in a fixed-point format, are recorded in the ROM memory, while only 8 bits of the fractional part are stored in the memory, since the integer part is always equal to 0.
The quantization process in the codec is implemented as follows: as soon as the next twenty-bit element of the resulting linear transformation matrix is calculated and transferred from the additional code to the straight line, it is determined whether this element is a low-frequency coefficient and, if so, bits 19 through 12 are written into the eight high order bits of the intermediate sixteen-bit register, the 8 least significant bits of this register, in this case, are filled with zeros (bits 11 to 0 of the original twenty-bit word are discarded, so about there is a division operation by 4096).
If the element is a high-frequency coefficient, then 0 is written in the most senior bit of the intermediate register, bits from 18 to 12 of twenty-bit words are written in the next seven bits, and the 8 least significant bits of the intermediate register are also filled with zeros. The outputs from this intermediate register are connected to one of the input ports of the 16x16 multiplier, the values from the ROM memory, where the fractional parts of the quantization coefficients raised to the power of -1 are stored, are sent to the other port of this multiplier. Moreover, zero values are supplied to the 8 senior pins of the port, and values read from the ROM memory to the 8 lower pins.
Далее, с тридцатидвухразрядного выходного порта умножителя считывается результат квантования, в котом 16 младших разрядов – дробная часть, которая отбрасывается, а 8 разрядов, стоящих непосредственно перед фиксированной запятой, это значащая часть (я думаю и так понятно, что результат квантования – это дробное число, представленное в формате с фиксированной точкой). Причём, в случае с низкочастотными коэффициентами, значащей частью являются не 8, а 7 разрядов, стоящих непосредственно перед запятой, в восьмой разряд здесь переписывается знак, полученный ещё на этапе базового преобразования, находящийся в самом старшем разряде:
Ну и далее, сформированные восьмиразрядные значения записываются в буферную память RAM в адресное пространство 00h – 3Fh:

Ready data from the buffer memory is read in accordance with the zigzag scan algorithm (what zigzag scanning can be read here ) and go to the stage of encoding the lengths of the series.
Decoding goes in reverse order. And here we are already operating with fifteen-bit data: the 6 least significant bits - the bits that are lost when dividing by 64, 8 bits - a significant part, 1 bit - a sign. Total: 6 + 8 + 1 = 15:
At the first stage, received in the operating unit, performing the inverse discrete cosine transformation, an eight-bit word is expanded to a fifteen-bit. To do this, first check to see if the byte arrived is a low-frequency coefficient, and if so, then all 8 bits are overwritten into the 8 least significant bits of the fifteen-bit word. And if a high-frequency coefficient has been received, then the 7 least significant bits of the byte received are overwritten into the seven least significant bits of the fifteen-bit word, and the highest digit containing the character is written to the highest digit of the fifteen-bit word.
Then, the data expanded to 15 bits is written to the RAM buffer memory in the address space 00h - 3Fh in accordance with the zigzag scanning algorithm. After the matrix of quantized DCT coefficients of size 8 by 8 is formed in the RAM memory, the process of inverse discrete cosine transformation begins, as described above. In this case, every fifteen-digit word read with RAM, first goes through the restoration procedure (the inverse to quantization procedure) by multiplying by the corresponding quantization coefficient stored in the ROM memory.
Here, the fourteen-bit word is multiplied by an eight-bit quantization coefficient, which is an integer (these are the values that were raised to the power of -1 when compressed). Next, matrix multiplication is carried out as described above. After that, the low-order bits are discarded from the resulting fifteen-digit values (division by 64) and the sign digit is checked, and if its value is 0, then the next eight bits contain the resulting value of the decoded component Y, Cb, or Cr (depending on which component plane decoded). And if the sign digit is 1, then the next 8 digits are simply reset (i.e., rounded to 0, because the result of the inverse DCT cannot be negative).
The obtained eight-bit results of the inverse DCT are written into the RAM buffer memory, thus forming an 8 by 8 image block. After the block is formed, each of its elements is written to the external SRAM memory at the corresponding address, forming, in turn, the final image in space YCbCr.
Walsh Transformation
And now, finally, we got to the point for which everything was up to. The Walsh transformation is a type of basic transformation, the transformation matrix of which is as follows:

Information about where this matrix comes from, how it is derived and how it is formed can also be found on the Internet or in textbooks on the theory of circuits and signals. We will not dwell on this.
So, as mentioned above, the basic transformation is reduced to multiplying the transformation matrix by the matrix of source data, after which the result is again multiplied by the transposed matrix of the same transformation. The values of all the elements of the Walsh transform matrix are either 1 or -1; accordingly, only the operations of adding data presented in the additional code will be required to perform hardware operations. If we paint the process of multiplying the Walsh matrix by the original matrix of the image block 8 by 8, we get the following expressions for each row element of the intermediate matrix:
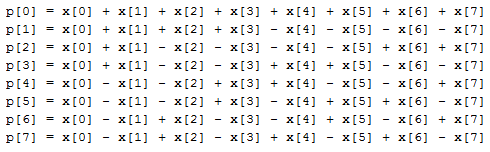
Where:
p [0..7] - the next row of the intermediate matrix;
x [0..7] is the next row of the original matrix, which is an 8 by 8 image block.
And further, if we paint the process of multiplying the intermediate matrix by the transposed Walsh matrix, we get the following expressions for each column element of the resulting matrix:

Where:
y [0..7] is the next column of the resulting matrix;
p [0..7] is the next column of the intermediate matrix.
As in the case of DCT, the upper left element of the resulting matrix will be a low-frequency coefficient, the value of which is always greater than 0, and the remaining 63 elements will be high-frequency coefficients, the values of which can be either less than or greater than 0 (as well as with DCT) .
Hardware, the Walsh transform block is a group of adders connected in a certain way, the inputs of which are first fed into the rows of the original matrix, the results are stored in a buffer, and then the columns of the previously obtained matrix are fed from the buffer to the inputs of the same group of adders. It should also be taken into account that with the direct Walsh transformation, the values of the elements of the resulting matrix can go beyond 255, so they will need to be divided by 64 or shifted by 6 digits to the right.
The inverse Walsh transformation is carried out in exactly the same way with the only exception that the elements of the resulting matrix, which will be an 8 by 8 image block, need not be divided by anything, the values are already normalized.
So, in the direct Walsh transform block, the incoming eight-bit component values, by analogy with the DCT block, are expanded into fifteen-bit ones (6 bits - bits that will be lost when divided by 64, 8 bits - significant bits, 1 bit - sign) and are written to the buffer memory RAM As soon as an 8 by 8 matrix is formed in the buffer, the elements of the original matrix are read out from the buffer, converted, and written to the addresses of the same line from which they were read. This makes it possible to use RAM memory with 64x15 organization (in the case of DCT, a buffer with 128x21 organization was required), but Quartus II allowed creating a RAM memory block with 64x16 organization only, one bit remained unused (although in the case of DCT 11 bits were not used).
Then, the columns of the matrix obtained in the previous step are already read from the buffer, converted, and the result of this conversion is transferred from the additional code to the direct one, after which the quantization operation is carried out exactly as in the case of direct DCT, the result of which is written to the RAM buffer memory, from where then read in accordance with the zigzag scanning algorithm. The inverse Walsh transform is carried out similarly to the direct one, the incoming data is then written into the RAM buffer in the zigzag scanning algorithm, and when read for the direct Walsh transform, they are multiplied by the corresponding quantization coefficients.
Below, in comparative form, the results of the operation of the direct Walsh transform and direct discrete cosine transform blocks are presented:

At the top left is a photograph on which we are training, which was first translated, say, inside our debug board, from the RGB color space to the YCbCr space, then each component plane was divided into 8 by 8 blocks and converted according to the direct Walsh transform rule. At the top right is the same photograph converted according to the direct DCT rule. Bottom left is the result of the Walsh transform subjected to the quantization operation, respectively, bottom right is the subjected to the quantization operation, the result of direct DCT read from the debug board.
Series Length Coding
The series length encoding algorithm is also called, in a different way, a compression algorithm that uses run length exclusion (RLE). This algorithm is based on the principle of determining groups of identical, consecutive characters (bytes with the same values), and replacing them with a specific structure containing the number of repetitions and a code of repeating characters, i.e. <number of retries> <repeated character (byte)>. Obviously, the maximum number of identical characters (data bytes) that can be encoded with such a structure depends on the length of the number of retries code.
For implementation, it was decided to choose an algorithm that is implemented in the graphic .pcx format. In this RLE algorithm, the peculiarity is that the number of repetitions is encoded by the counter byte, in which the upper two bits contain units, and the lower six contain the number of repetitions. Accordingly, the values of bytes that are not repeated in a row and whose values are less than C0h are transferred to the compressed data stream without change. And byte values that are not repeated in succession are large C0h, (two units in the upper digits), when written to the output stream, in any case, are preceded by a counter byte, and, since there is only one such symbol in the stream, the byte counter takes on the value C1h. It should also be taken into account that the maximum number of retries that can be encoded in six allocated bits is 63 = 3Fh, therefore, after each entrapment of the retry counter, it is necessary to check if its value is 63, and if so, into the output stream, first,
Например, на выходе блока базового преобразования (будь то блок прямого ДКП или быстрого преобразования Уолша) имеем следующий поток данных, выдаваемых с буферной памяти RAM в соответствии с алгоритмом зигзаг-сканирования: ECh, C2h, 03h, 0Ah, 0Ah, D1h, D1h, 01h, 01h, 01h, 00h, 00h, 00h, 00h, 00h, 02h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h, 00h. Тогда, после кодирования данного потока, алгоритмом RLE, получим следующий поток данных: C1h, ECh, C1h, C2h, 03h, C2h, 0Ah, C2h, D1h, C3h, 01h, C5h, 00h, 02h, F0h, 00h.
In total, in our case, from a string of length 64 bytes, after compression, a string of length 16 bytes was obtained, in which the largest number of repetitions belongs to zero bytes. These zero bytes are rounded to zero after quantization, high-frequency coefficients, respectively, if quantization is not carried out, the number of consecutive zero bytes will be significantly lower, which will give a lower compression ratio, but will save image quality.
Hardware-wise, this algorithm is implemented quite simply both during compression and during unpacking.
When unpacking after receiving the next byte, we check its most significant two bits, and if their values are equal to one, then load the least six bytes into the counter, read the next byte without checking its most significant bits, put it into the output stream, decrementing, at the same time, the counter until it is zeroed, after which we read the next byte from the stream, and if the values of the highest bits of the counter are different from two units, then we rewrite this byte into the output stream without changes.
In the codec, the RLE encoding algorithm is executed by the control device while reading data bytes from the basic transform unit during compression, the RLE decoding algorithm is executed before the data is loaded into the basic transform unit during unpacking (I think this is clear).
Huffman Compression
More than one article published on this site has been devoted to the Huffman algorithm; therefore, as before, I will not dwell on theory. I can only say that, by analogy with the JPEG algorithm, in the device described here, I implemented the Huffman algorithm with pre-computed, fixed tables.
The difference from the JPEG algorithm is that only the code lengths are stored in the tables in the JPEG, and not the codes themselves, in the same device, sixteen-bit Huffman codes are stored separately in one ROM memory, and the number of significant bits in each of the ROMs is stored sixteen-digit codes, starting with the oldest. Also, in JPEG, different tables are used for low-frequency and high-frequency coefficients, and instead of the low-frequency coefficient values themselves, their differences are encoded. In my device, I didn’t complicate things this way (maybe in vain) and, in the device I developed, all the coefficients are encoded in a single stream and a single table.
The encoding is carried out as follows: the address inputs of the ROM memory blocks are encoded bytes (a data stream encoded by the RLE algorithm), while the number of bits whose value was read from the output of another is read from the output of the ROM memory block, where the Huffman codes are stored ROM memory block. Huffman codes and their lengths are stored at those addresses whose values correspond to the values of the encoded bytes.
Further, from the read bit stream, bytes are formed and written into memory. For example, when encoding one byte, 4 bits were read from the ROM containing the Huffman code, while encoding the second byte in the stream - 11 bits, the third - 3, and the fourth - 4. Total, we get 4 + 11 + 3 + 4 = 22, 22 bits are divided by 8, we get 2 bytes and 6 bits, to which we append, in the least significant bits, two zero bits (the last byte in the stream is encoded) and we get 3 equivalent bytes, which are written to external memory, i.e. . out of four bytes at the input, three were received at the output.
The Huffman decoder is implemented in the form of a truth table, in the AHDL language (in this language, a special “TABLE” operator is provided for this, although it could be done in Verilog using the “case” operator, as you like), which has one a sixteen-bit input port for the Huffman code and one five-bit input port for the length of this code.
Decoding is carried out as follows: byte is read from the SRAM external memory, which is bitwise loaded into the sixteen-bit register, starting from the high-order bit, the outputs of which are connected to the sixteen-bit input port of the Huffman decoder (the same table), after loading the next bit, the counter connected to the other is incremented Huffman decoder port.
After loading the next bit, the signal is checked, meaning that the input combination of the Huffman code and the length of the code, the output byte is found, and if the value of this signal is a logical unit, then the byte is read from the output port of the Huffman decoder, which goes to RLE decoding. In this case, the sixteen-bit register is reset, and the bits remaining in the byte are loaded into it again from the high order, if the bits in the byte read from the external memory are expired, then a new byte is read, etc.
Checking the operation of the codec in the complex
At the first stage, an encoder was compiled and flashed into the FPGA, which performs compression based on the fast Walsh transform, with quantization of the coefficients. As a result, uploaded by UART to the device, our test image of 256 by 256 pixels in size with a memory capacity of 192 Kbytes was converted (compressed) into a file with a memory capacity of 8.1 Kbytes.
At the second stage, an encoder was compiled and flashed into the FPGA, which performs compression based on the fast Walsh transform, but without quantization of the coefficients. As a result, the same image was converted (compressed) to a file with a storage capacity of 43.8 KB.
At the third stage, an encoder was compiled and flashed into the FPGA, which performs compression based on a discrete cosine transform, with quantization of the coefficients. As a result, uploaded by UART to the device, our test image of 256 by 256 pixels in size with a memory capacity of 192 Kbytes was converted (compressed) into a file with a memory capacity of 8.17 Kbytes.
At the fourth stage, an encoder was compiled and flashed into the FPGA, which performs compression based on a discrete cosine transform, without quantizing the coefficients. As a result, the same image was converted (compressed) to a file with a storage capacity of 35.9 KB.
Below are the results of unpacking, developed by the device, previously compressed images.
На рисунке, представленном ниже, в центре показано исходное изображение, слева – изображение, сжатое с квантованием коэффициентов, при помощи быстрого преобразования Уолша, справа – изображение, сжатое с квантованием коэффициентов, при помощи дискретного косинусного преобразования:

Разницу в базовых преобразованиях отчётливо при увеличении одинаковых участков изображений. Так, преобразование Уолша даёт более контрастные границы на участках переходов, в свою очередь, ДКП делает переходы на границах более плавными.
Ниже представлены результаты распаковки изображений, которые сжимались без квантования коэффициентов. Также как и в предыдущем случае, в центре — исходное изображение, слева – изображение, сжатое при помощи быстрого преобразования Уолша, справа – при помощи ДКП:

At first glance, there are no special losses in quality, but if you enlarge the image, you can see the borders of 8 by 8 blocks, which, in the case of the Walsh transformation, also have more contrasting borders, and in the case of DCT, they are smoother. In general, a number of works have been written regarding issues of assessing image quality, and I don’t really want to do this here.
Summarizing
And so, below is a table containing the results of determining the compression characteristics obtained on the developed device, an image measuring 256 by 256 pixels in .bmp format with a memory footprint (L) of 192 KB. The size of the original image is calculated as follows: 256 × 256 = 65536 pixels, each byte has three bytes (1 byte is the red component, 1 byte is the green component, 1 byte is the blue component), we get 65536 × 3 = 196608 bytes, plus 53 bytes - the header, total we get 196661 bytes or 196661/1024 ≈ 192 KB with "pennies":

It can be seen from the table that both methods of basic conversion in hardware implementation give practically the same results, with the exception of time and speed of compression / decompression. Here, the Walsh transform wins over the special case of the Fourier transform - DCT. 1 - 0 in favor of the Walsh transformation.
If we compare both types of conversions in terms of the cost of FPGA hardware resources, we get the following:
From the screenshots shown, it is clear that the FPGA hardware resources, both conversions consume the same, except for the use of built-in multipliers. Here, a special case of the Fourier transform again lost to the Walsh transform. Total: 2 - 0 in favor of the Walsh transformation.
In principle, we can conclude that, from the point of view of hardware implementation, it is better to use, as a basic transformation, the Walsh transformation.
Well, in the very conclusion, I want to note that this hardware codec for image compression / decompression was developed, let's say, thoughtlessly and thoughtlessly. This explains the unsatisfactory (at least it seemed to me) values of the temporal characteristics of compression / decompression. Looking through the project again and again, I always find optimization opportunities and options for reducing the image processing time, while increasing the size of the processed (compressed / unpacked) image. As a result, it will be possible to achieve a compression / decompression speed of 24 images per second, which will allow processing video streams.
Well, that’s all. Thanks for attention!
