Twisted architecture

Translation of Christopher Carlson's " Twisted Architecture " post .
I express my deep gratitude to Kirill Guzenko KirillGuzenko for help with the translation.

---

Я не ставил перед собой задачу скрутить Херст-тауэр (Hearst Tower) Нормана Фостера в ленту Мёбиуса и отправить его в космос, или заставить его Мэри-Экс танцевать танго с самим собой, просто я увлекся. Это один из профессиональных рисков работы с Mathematica.

Всё началось с невинного эксперимента в лофтинге — методике также известной как обтягивание (skinning), пришедшей из судостроительства. Целью моего исследования были некоторые трёхмерные формы, а лофтинг казался отличным способом быстро добиться результатов. Я написал функцию Loft, которая принимает упорядоченное множество трёхмерных контуров и обтягивает его полигонами.



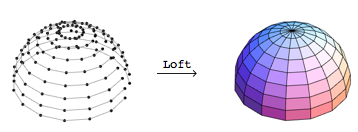
Для декомпозиции геометрии полигонов из их топологии Loftuses the GraphicsComplex primitives in Mathematica . The coordinates of the contour points are collected in the first argument. The second argument is a list of polygons ( the Polygons ), the coordinates of which are replaced by integer indices in a coordinate list. It was not difficult to write the Loft function , but it took some imagination to index the polygons associated with the desired points.



I worked with Loft through the Manipulate function , and was very pleased to discover some new and interesting forms in my research. You can download the demo and try it for yourself.





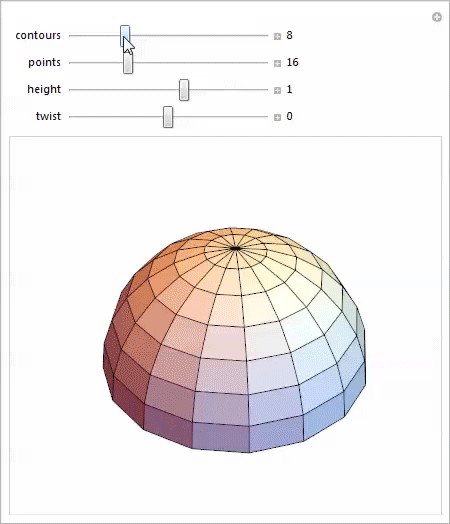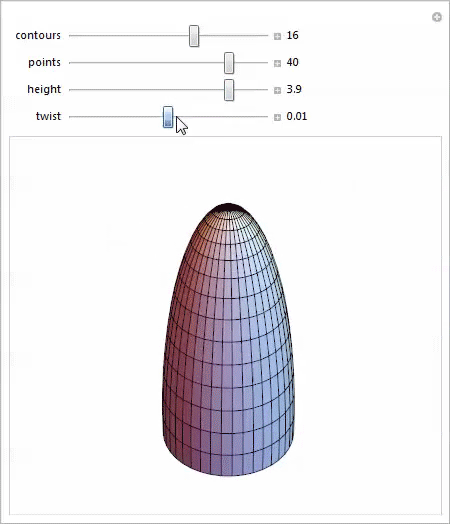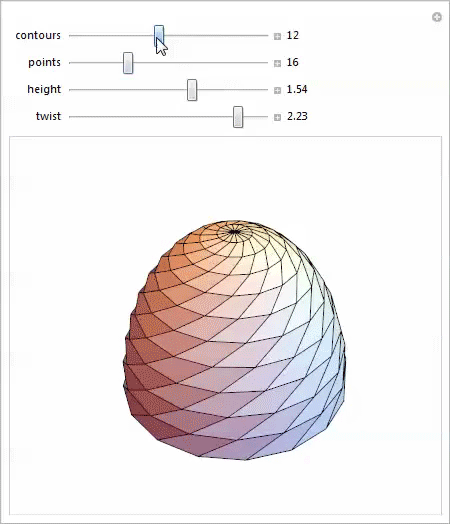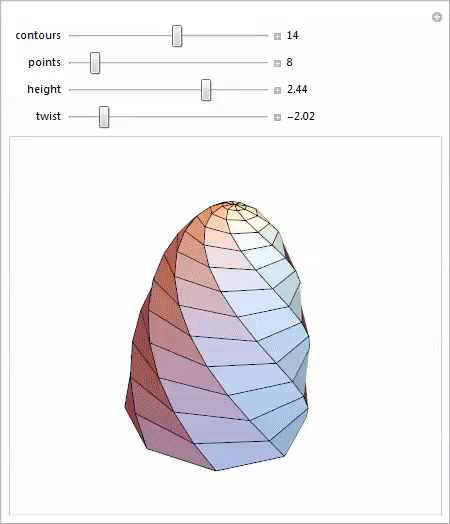
Even this trivial parameterization of a scalable twisted hemisphere gives an amazing variety of shapes, each of which offers interesting possibilities for study.



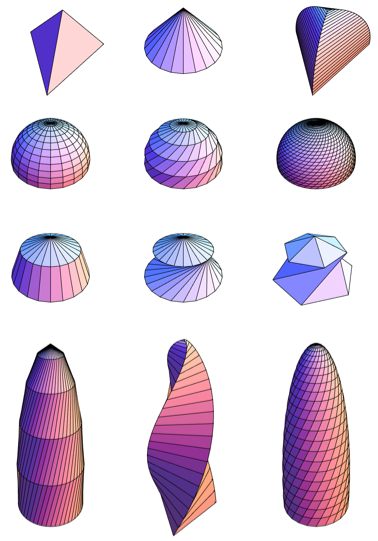
The last of these forms led me to think of the Norman Foster Swiss Re building in London, which locals call a cucumber (hereinafter referred to as Mary-Ex). I was surprised how plausible the Mary-Ex model is in Mathematica. It was immediately clear that my simple Loft function would not be able to cope with the creation of the Mary-Ex diagonal grid, so I decided to generalize this function first. Step by step, and now I already had a much more flexible Build function




, with the help of which I had the opportunity to model not only Mary-Ex, but also many other architectural forms based on a combination of panels and their frames.

My Build function works like Loft , but it gives me much more flexibility in specifying elements such as tubes and polygons and algorithms for their placement on the contour grid. Like Loft , Build's first argument is a set of paths. The second argument is a list of Graphics3D primitives that contain an additional argument that defines the algorithms for their placement on the contour grid.

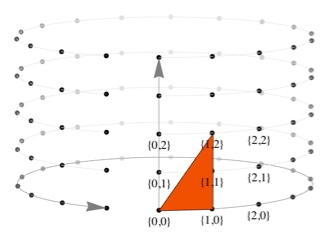
If we represent the contours numbered from the bottom up and the points on the contour from left to right, then the indices{point, contour} will correspond to the coordinates of the integer coordinate system.

This is how the Polygon primitive [{{0,0}, {1,2}, {1,0}}] is placed on the grid.



A primitive that does not contain an additional repeat argument is automatically copied over the grid. An explicit way to indicate the type of placement of copies of an element is done by defining a pair of transfer vectors, as in Polygon [{{0,0}, {1,2}, {1,0}}, {{2,0}, {1,1}} ]. Here is how this polygon will be placed on the grid:



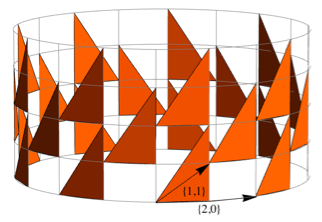
In linear primitives, such as Line and Tube , the repetition argument specifies the frequency with which primitives are broadcast horizontally, and for horizontal primitives, vertically. Combining repeats of polygons, tubes and lines, Buildgives me a lot of flexibility in the task of assembling from panels and structural elements. Here is an abstract structure that I created to demonstrate the use of Build primitives .





Now that I have Build , my next task is to determine the shape of the Mary-Ex profile and build the corresponding contour grid. As always, trying to find the easy way first, I first experimented with flattened ellipsoids, and as a result I found that the top of Mary Ax is too sharp for the ellipsoid. No other simple mathematical form came to my mind, so I decided to set the outline of an arbitrary shape through splines.

I remembered this potter 's wheel demonstration ( Potter's Wheel Demonstration), written by my colleague Yu-Sung Chan for modeling bodies of revolution of arbitrary shape. That was exactly what was needed. Opening Mary-Ex's photo in a separate notebook, I moved the points of the spline profile until I got an acceptable approximation of its shape. When I was satisfied with the result, I used “Paste Snapshot” in Manipulate to get the source code for this shape. From the source code, I took the coordinates of the spline control points and inserted them into the BSplineFunction , which sets the profile. The final step was to split the curve profile into equally spaced horizontal sections. Mathematica 's versatile meshing features allow you to do this.

















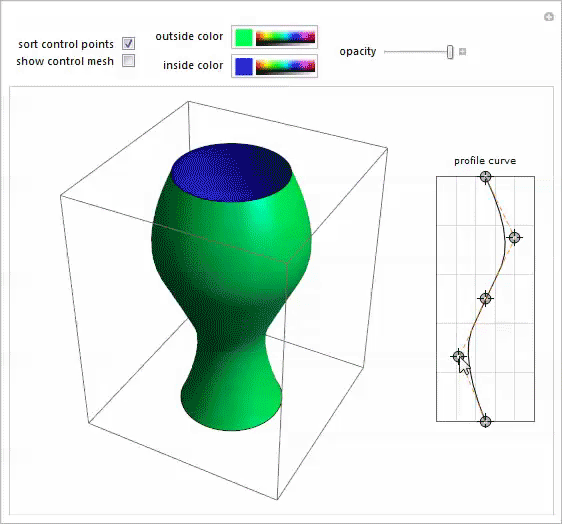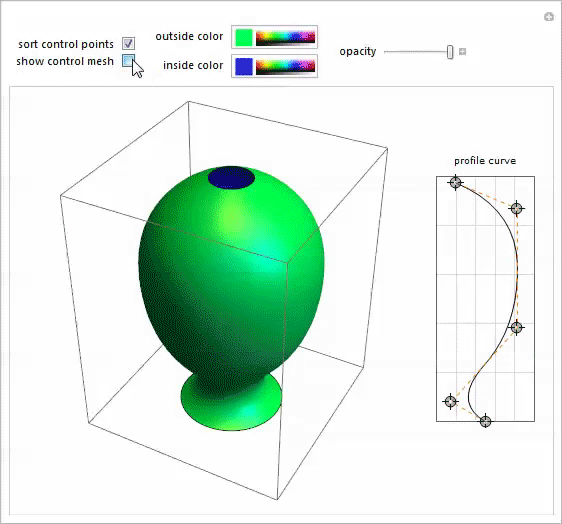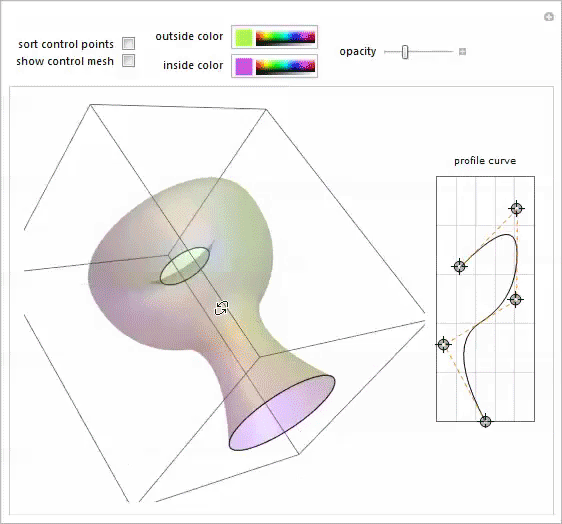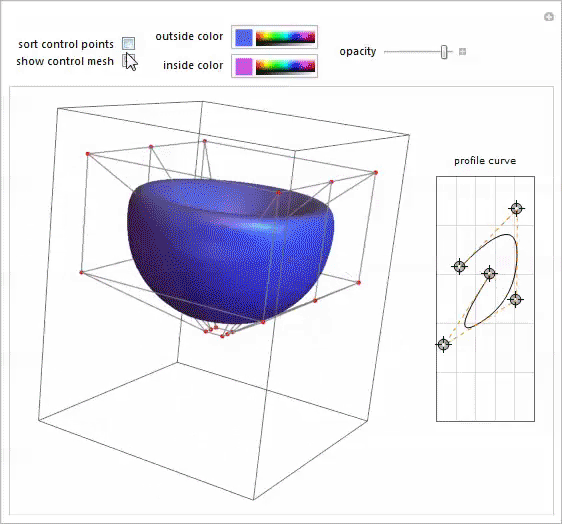
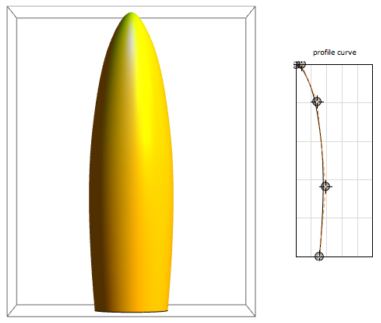
I extracted the coordinates of the grid points from the plot result , added the profile boundary points, and sorted the coordinates by y to get a list of points from which I could build a Mary-Ex contour grid.



The contours themselves correspond to the body of revolution, moreover, the radial coordinate of the profile points is x , the height coordinate is y , and the number of points around the contour is twice the number of Mary-Ex glass panels.



I tested Build for the correct display of contour points. It turned out what you need.





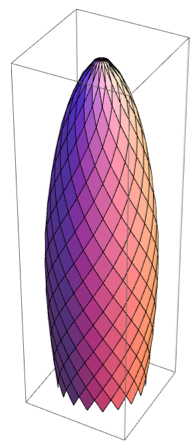
As a final step, I found the coordinates of the contour points of the bordering ring at the top of Mary Ax and added it.

I will not deny that it took quite a lot of painstaking work with Build to build a ready-made model. The Mary Ex building, the roof, the upper dome, the rings, the borders and the transitions between the individual parts - all required an individual approach. To select the properties of materials and lighting, I used Manipulate and twisted the sliders until I got the desired values. And here is the result.



After I got the finished model, I could start researching it. One of the unique benefits of Mathematicais the ability to post-process structures through the use of replacement rules. The final model of Mary-Ex was presented in the colors that I set for the dark and light panels of the building. Replacing these colors with new ones, I created this color variation based on the British flag.









Post-processing using replacement rules can be applied not only to the appearance attributes of an object, but also to its geometry. And the fact that all of the coordinates of my model are in the first argument of GraphicsComplex makes coordinate conversions especially easy. And since all graphic primitives are attached to the same coordinates, the primitives will automatically move along with the coordinates during their transformations.

Using this technique, I wrote this Manipulateto study variations in radial geometry Mary-Ax.





Now I have the opportunity to get answers to some interesting questions. But what if Mary-Ex were two-sided rather than round? Trilateral? Four way?



But what if the dark components of Mary Ex were sunk into the building? But what if the recesses were opposed to them? But what if London were shocked by a truly strong earthquake?



Answers to all these questions can be easily obtained with Manipulate in Mathematica . Surrealism - is simply defined as the distance by which the slider is moved from its position corresponding to "reality". My research ended somewhere around this (in Dali style) Mary-Ex dancing with herself.



Inspired by the results of my work with Mary-Ex, I turned my attention to another diagonal mesh Foster building - the Hearst Tower in New York. Compared to Mary Ex, the Hearst Tower simulation was a trifle. The only difficult moment was the creation of corner areas with alternately protruding and drowning polygons. The rest was for the simple use of the Build function . Here is my model of the basic structure of the tower, visualized with default lighting in Mathematica . The structure of the tower is created by periodic broadcasting of polygons. For fun, I replaced the broadcast with rotation, and after adding several floors, I created this curved tower, turned into a torus.











Deciding to go further, I spent a couple of seconds to add a second rotation around an axis perpendicular to the first and created such a "mebius" building. I like this beautiful rhythm generated by the combination of a diagonal grid with bends and ornate mobius surfaces.



Perhaps on Earth, the Mobius building would be difficult to sell. But I imagine it floating in space - the space gallery of fine arts - a kind of Guggenheim orbital gallery with a twist in which visitors say something like:

Do not forget to put on your velcro slippers and soft helmets ala 2001: A Space Odyssey and pay attention to the works hanging on the wall to your right. After you make a circle around the gallery, you will hang on the ceiling, looking at the opposite wall, which, of course, is the same wall - because it is the only one in the gallery. Enjoy the view of the Milky Way, and possibly the Earth flying somewhere far away.