A detailed look at Leibniz's legacy

Перевод статьи Стивена Вольфрама (Stephen Wolfram) "Dropping In on Gottfried Leibniz".

На протяжении многих лет меня интересовала личность Готфрида Лейбница, в частности из-за того, что он хотел создать что то на подобие Mathematica, Wolfram|Alpha и возможно даже A New Kind of Science но на три столетия раньше. Поэтому когда в недавнем прошлом я посетил Германию, то мне страстно захотелось побывать в его архивах в Ганновере.

Листая пожелтевшие от времени, но все еще прочные листы с его записями я чувствовал некоторую взаимосвязь — я пытался представить, о чем он думал когда писал их. Также я старался сопоставить содержимое записей с тем, что мы знаем сейчас — три столетия спустя.



Some things in mathematics do not change over time - for example, here Leibniz wrote the expansion of the square root of two (the text is written in Latin):



Or here Leibniz tried to calculate the continued fraction - and although there is an arithmetic error , he nevertheless brought result to the end (P - in his early notation denoted an equal sign).



And here you can see some points from mathematical analysis, which can be found practically in this form in modern textbooks.



But what was the essence of his main work? What did Leibniz reflect on most of his time?

I have always considered Leibniz an ambiguous personality. He did a lot of seemingly unrelated things - in philosophy, mathematics, theology, in legislative affairs, physics, history and other fields. He described all his achievements in the seemingly strange manner of the 17th century.

But over time, I began to better understand Leibniz as a person, and it became clear to me that almost everything he did was aimed at achieving a common goal, which, oddly enough, is very similar to the one to which I aspire today.

Gottfried Leibniz was born in Leipzig in 1646 (now it is a German city). He was born four years after the death of Galileo and the birth of Newton. His father was a professor of philosophy and his mother was from a family of booksellers. Leibniz's father died when he was 6, but only two years after he was allowed to use his father’s library. Leibniz began to read everything in one gulp. At 15 he entered a local university, studied philosophy and law. At 20, he received diplomas in both areas.

As a teenager, Leibniz showed interest in the systematization and formalization of knowledge. At that time there were only vague ideas about the systematization of knowledge, for example, in the semi-mystical work Ars Magana (lat. Great art) written by Raimund Lull ( Ramon Llull) in the 1300s, you can try to find a description of a universal system in which all knowledge can be derived from combinations of signs belonging to (as Descartes called it) the "alphabet of human thought." In his thesis on philosophy, Leibniz adhered to this idea. He used the simple principles of combinatorial mathematics to calculate the number of possibilities, talked about the decomposition of ideas into simple components that you can work with using the "logic of invention". And to evaluate his method, he included in the work a task whose solution was to prove the existence of God.

As Leibniz himself later said, these theses written at the age of 20 were mostly naive. But it seems to me that they already characterized Leibniz's way of thinking with which he did not part throughout his life. For example, his diploma in law on “baffling legal cases” was devoted to how these cases can be resolved using logic and combinatorics.

Leibniz was supposed to become a professor, but instead, he decided to start working as an adviser to various judicial and political figures. Quite often, he conducted research, analyzing the dark places of their family tree and history. He also systematized their libraries, various legal codes, etc. Sometimes, he had to solve various engineering problems, for example, how to best protect silver mines from water. However, in the beginning, most often these were just consultations on political maneuvering.

Because of one such case, in 1672 Leibniz had to leave for Paris for 4 years - during this time he communicated with many leading enlighteners of that time. Prior to this, Leibniz's knowledge in mathematics was only superficial. But in Paris, he studied all the most modern ideas and methods. In particular, he sought out Christiaan Huygens, who agreed to teach him math after he managed to pass the test to find the sum of inverse triangular numbers .

Over the course of several years, Leibniz honed his ideas on the systematization and formalization of knowledge, developing the architecture of what would make knowledge, in a modern language, computable. He saw the first step in developing ars characterisitca- a methodology that would make it possible to put symbolic representations in line with certain things, thereby creating a homogeneous “alphabet of thoughts”. Then - as he believed - this alphabet will allow you to find "truths in all areas, using mathematics, whether it be arithmetic or algebra."

He came up with many ambitious names for his ideas: scientia generalis (“general method of knowledge”), lingua philosophica (“language of philosophy”), mathematique universelle (“universal mathematics”), characteristica universalis (“universal system”) and calculus ratiocinator("Math of thought"). He saw many applications to his ideas in almost all areas of life - law, medicine, engineering, theology, etc. But he achieved the greatest success in mathematics, and this happened quite quickly.

In my opinion, the most remarkable fact is that in the history of mathematics the question of notation has rarely been raised. This happened at the beginning of the development of modern mathematics at the end of the first decade of the 19th century thanks to the work of people such as Gottlob Frege and Giuseppe Peano. And in the modern world this happened thanks to my work on creating the Mathematica systemand Wolfram language. However, a similar event also happened more than three centuries ago thanks to Leibniz. And it seems to me that Leibniz's successes in mathematics are largely due to how hard he worked with the problem of notation, with what clarity he talked about mathematical structures and related concepts.

If you look at his notes, you will see in an explicit form the process of developing notation. Many things look modern, but not without the charm of the 17th century, for example, the use of symbols of alchemy or astronomy to denote algebraic variables.



Here the symbol P is used instead of the equal sign. Leibniz had an interesting idea that when the legs of P are equal - this is equality, when, for example, the left leg is longer, this is equivalent to the “>” sign and vice versa.



Dashes over parts of expressions are used for grouping - I like the idea more than brackets, although it would be more difficult to enter them from the keyboard.



We use such dashes for square roots, but Leibniz wanted to use them also in integrals together with the symbol “d with a tail” which reminds me of one of the symbols in Mathematica that we created to represent the integrals to the system.



In particular, when solving equations, the symbol “±” is quite common and therefore often there is confusion about how to group variables in an expression, say, a ± b ± c. It seems that Leibniz also considered this a very uncomfortable obstacle and he presented a notation that would be useful to use today.



At the expense of some notation, I do not have unambiguous thoughts, although many of them, for example, “ tildes on top ” look pretty nice.



As well as these elements with dots:



Or here something similar to diagrams ...



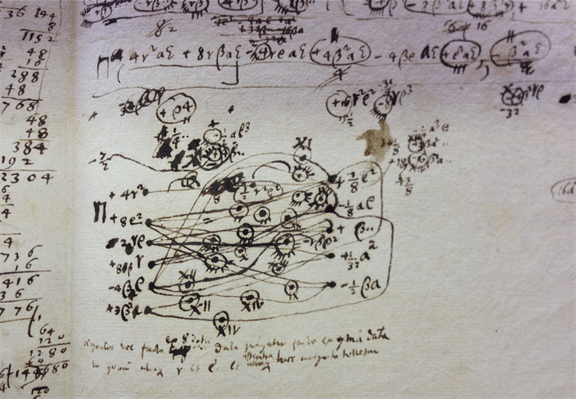
Of course, the most famous elements of Leibniz notation are the integral sign (long s) and d (in the fields on the right). They were presented together for the first time on November 11, 1675, then 5 in the 1675 record was replaced by 3, probably by Leibniz himself.



It seemed interesting to me that all of its notations for various operators are very different from logical operators. The operator “or” is just a Latin translation of vel, “and” - et and so on. And when he came up with quantifiers (universality and existence), he designated them with abbreviations in Latin UA and PA.



It always amazed me that the idea of ​​creating a universal language for operating with any data appeared only in the thirties of the twentieth century. Therefore, I was wondering if the first sketches of such a system could be hidden in the writings of Leibniz - take at least the diagram just examined, which we can now call some kind of Turing machine. But over time, having studied more information about Leibniz himself, I realized that this is not the case.

One of the main evidence of my assumption is that Leibniz did not seriously consider discrete systems. He called the results of combinatorial calculations “obvious and not requiring evidence”, presumably because, he believed, they could be confirmed using simple arithmetic. And he developed the mathematical apparatus only for “geometric” or continuous mathematics. In describing the properties of curves, Leibniz already proposed an analogue of continuous functions, but it never occurred to him to apply the same principle to discrete mathematics, which could, for example, lead him to the idea of ​​universal elements for constructing functions.

Leibniz understood the significance of the apparatus of infinitesimal values ​​developed by him and wanted to develop similar “calculuses” for other fields of knowledge. Another idea close to a unified system of knowledge was encoding logical properties. He wanted to match a prime number to every possible property, and then each item could be characterized by the product of these primes. Such an approach would allow us to show the logical difference between objects using arithmetic operations. But he considered only static properties and he never came up with an idea similar to Gödel’s numbering, where operations are also encoded with numbers.

But even despite the fact that Leibniz did not come up with the idea of ​​a universal knowledge management system, he still understood that computing is primarily a mechanical process. And early enough in his life, he decided to build a real mechanical calculator for arithmetic operations. This is partly due to the fact that Leibniz himself needed a similar device (the best motivation for this kind of thing). Despite his mastery in algebra and the like, his works are full of touching touches in a column in the fields (sometimes with errors) that are reserved for posterity.



There were separate examples of mechanical calculators created during the time of Leibniz, and when he was in Paris, he no doubt saw a folding calculator created by Blaise Pascal in 1642. But Leibniz wanted to make a universal calculator that could perform four basic arithmetic operations. He also wanted the calculator to be easy to use, for example, turning the knob in one direction would mean multiplication, and in the other - division.

In the works of Leibniz, there are many drawings and diagrams of this machine:



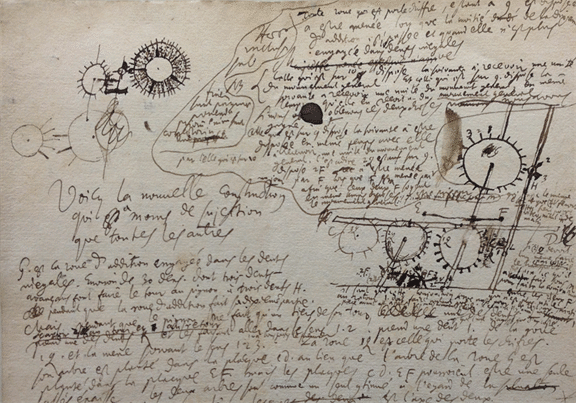
He imagined that his calculator would bring great practical benefits and a considerable share of his fantasies were ideas for the successful development of the business associated with the calculator. But unfortunately Leibniz was not able to make the calculator reliable - far from always he gave the correct result. Like most of the similar mechanisms of that time, the calculator was just an embellished pedometer (odometer). Leibniz faced the same problem as Charles Babbage two hundred years later - it is extremely difficult to make all the disks move at the same time, when necessary.

In the beginning, Leibniz created a wooden prototype that he hoped would be able to work with three-digit or four-digit numbers. But at preliminary shows in particular in front of Robert Hook (Robert Hooke) in London in 1673, the mechanism failed him. However, he continued to ponder on his improvement - in 1679, the work “Recent Improvements to the Arithmetic Machine” was published:



Notes from 1682 indicate that Leibniz encountered new problems:



But he had blueprints and ordered engineers to produce a copper version of the mechanism to work with a large number of numbers:



In particular, Leibniz even prepared “marketing material” for his car:



... and user instructions ...



Here is a complete model of the machine with instructions for use:



But despite all his efforts, the calculator still did not work. Leibniz worked on the calculator for forty years and spent a total of more than a million dollars on it when converted to the current rate.

When I visited his archive, I could not help but ask the curators about what happened to this calculator. “Hmm, we can show you” - was the answer. The calculator stood on one of the many shelves in the basement and looked completely new in its glass box - my own photo in which the past and the present are strangely intertwined:



The calculator has not lost a single detail. He was in a convenient portable wooden case with a pen for arithmetic operations. If it worked correctly, then in just a few minutes of turning this knob, we could get an answer to any question from the section of simple arithmetic.



Leibniz considered his calculator to be a practical project, but nevertheless he also wanted to use it to create a “logic” describing mechanical connections. He also reflected on the nature of numbers and arithmetic. He was also struck by binary numbers.

Bases other than 10 have been used for centuries in various entertaining mathematical examples, but Leibniz focused on base 2 because he considered it to be of particular importance and perhaps a bridge between philosophy, theology and mathematics. And when he learned about I Chang from missionaries from China, it only strengthened his faith. He regarded this work as akin to his characteristica universalis .

Leibniz came to the conclusion that it is possible to build a calculator for binary numbers, but at the same time he believed that only numbers with a base of 10 are of practical importance.

Today Leibniz's notes on binary numbers cause mixed feelings. One part of the work looks quite modern while the other clearly refers to the 17th century. For example, he argued that the binary system is proof that everything can be obtained from nothing, that 1 is God, and 0 is nothing.

After Leibniz, for another couple of centuries, the binary number system did not develop until the recent growth associated with the advent of computers. Therefore, Leibniz's calculations regarding the binary system can be safely called ahead of time:



Working with binary numbers, Leibniz was looking for the easiest way to describe the structure of things. And when he introduced the concept of "monad" he no doubt strove for the same thing. I must say, I can never understand the monads. When it seemed to me that I understand everything, there was some nuance that destroyed the whole integrity of the picture.

It always seemed to me tantalizing that Leibniz came to the conclusion that the best of all possible worlds is a world in which a huge variety of phenomena follows from the minimum possible number of premises. Indeed, at the time when I was just starting to work on NKS when I formulated and then studied one-dimensional cellular automata in 1981, I wanted to call them “polymons,” but at the last second I got scared as I got confused in monads again.

Around Leibniz and his labors, there was always a certain secret. Kurt Gödel (possibly in a fit of paranoia) was convinced that Leibniz discovered a great truth that was then hidden from society for centuries. But despite the fact that Leibniz’s work was seized after his death, this was due to the fact that the history and genealogy works contained information that could not be publicized, be it state or personal secrets of those in power.

The works of Leibniz were published a long time ago, but are still not fully understood. And the problem is not that there are too many of them. In total, it is about 200,000 pages that fill no more than a dozen bookshelves. This is just a little more than my personal archive, which I have been maintaining since the 1980s. The difficulty is caused by the heterogeneity of the material - not only different areas of knowledge, but also drawings created one on top of the other, notes and letters, the relationship between which is not fully understood.

The Leibniz document archive contains both very large documents:



very small ones (with age, Leibniz's handwriting has become smaller and more dense):



Most of the documents in the archive look very serious and scientific. However, despite the fact that paper at the time of Leibniz was quite expensive - he did not hesitate to spend it on funny drawings (maybe this is Spinoza?).



Leibniz maintained mail correspondence with hundreds of people - both well-known and not very well throughout Europe. And so 300 years later, in his archives you can find random letters from famous people, for example, from Jacob Bernoulli:



What did Leibniz look like? You can see the official portrait and the informal bust, on which there is no big wig, which served as the reason for ridicule even at that time. Presumably Leibniz wore a wig to hide a cyst on his head.



As a person, Leibniz was polite and restrained. In a sense, he could be called an eccentric who was trying to get to the bottom of things. It is believed that it was very difficult for him to tune into a conversation with the interlocutor. Only a few intellectuals of that time, including Leibniz, never married, but our hero nevertheless enjoyed success with the ladies.

As a man at court, Leibniz always sought to rise as high as possible, but without a passion for hunting or drinking, he did not fit into the higher circles for which he worked. Towards the end of his life, when Geogr I (George I) from Hanover became king of England, Leibniz had to go with him to England. But he was told that before he went there he had to write a historical work on which he had allegedly worked for 30 years. If he managed to finish it before his death and he was allowed to sail to England, then he could have had a very interesting dialogue with Newton.

In addition to his papers and the calculator, Leibniz’s archive has one more thing - a folding chair which he took with him while traveling and which he also used as a table in carriages to continue to write on the road:



Leibniz was always worried about his status - he often signed as Gottfried von Leibniz, although no one knew where this piece of von came from. As another insignia for his discoveries, he wanted to have a medal that would be dedicated to binary numbers. He developed a detailed appearance in which the inscription omnibus ex nihilo ducendis was present ; sufficit unum ("everything can be inferred from nothing; all that is needed is 1"). But no one did this medal to him.

In 2007, I wanted to come up with an unusual gift for the 60th birthday of my friend Greg Chaitin, who had been studying the life and works of Leibniz for many years. And I made for him the Leibniz medal. On the reverse side of the coin, instead of the image of the Duke proposed by Leibniz, we placed an inscription in Latin about the works of Greg.

When visiting the archive, of course, I took the medal with me:



It would be interesting to find out what inscription could have been on Leibniz’s grave. But when Leibniz died at the age of 70, his political career was in decline and no plaques were created. But when I was in Hanover I really wanted to see his grave - on which in Latin was written "Bones of Leibniz."



However, throughout the city, for example, Leibniz cookies are sold:



What can we say about Leibniz? If history had turned out differently, today there would have been a direct connection between Leibniz and modern computing. But everything turned out as it turned out and most of Leibniz's works remained on the sidelines - we can look at them only from the point of view of our current knowledge.

Now we know exactly what Leibniz was aware of and what he did not understand. He seized on the concept of a formal description and symbolic representation of a wide range of different things. He suggested that there are universal elements (for example, 1 and 0) from which any description can be created. He understood that if knowledge could be represented in symbolic form, then all the consequences would be only a matter of mechanics. This would create new knowledge by listing the various options.

Some of Leibniz's works were annoyingly abstract and philosophical. But in others, he showed examples of a purely practical approach. He was skilled enough to actually make progress. His typical approach to the problem was, first of all, to try to create a formal description using formal notation whenever possible. Then he tried to create a certain mathematical apparatus using which it would be possible to derive a solution to this problem.

In truth, he achieved success only once, working in the field of continuous "geometric" mathematics. It is a pity that he never tried to seriously engage in discrete mathematics, since, it seems to me, he could achieve significant results in it and perhaps reach the idea of ​​universal computing. He could also get to an attempt to renumber possible systems by analogy with how I did in the computing universe.

He tried to apply this approach in law, but at that time it was too early. Only now - 300 years later - does this idea begin to seem realistic.

Leibniz also worked in the field of physics. He achieved some significant results, in particular with regard to kinetic energy, but he never tried to offer a complete picture of the world by analogy with Newton and his Principia .

In a sense, I think Leibniz could not do more because he tried too hard to find practical application for his research and - like Newton - tried to describe real physical processes, rather than to operate with abstract structures. If Leibniz tried to conduct at least a little research by analogy with what I did at the NKS, then, in my opinion, he would not have any difficulties with this, and the history of science could go in a completely different direction.

At one time, I realized that Newton was able to defeat Leibniz the information war for who first invented the apparatus of mathematical analysis, but the main prize in this war was the opportunity to lay down his own view of science and the world, as fundamental to the generations ahead. Newton was more practical - he invented tools for calculations related to the real world. While Leibniz had broader and philosophical views, he saw the mathematical apparatus not as a tool to achieve its goals, but as an example that should inspire the development of other ways of formalizing knowledge in other areas.

I often think that my way of thinking, my beliefs about how to work with knowledge in the modern world is something obvious and something that will inevitably come if you start to think about the world from a formal point of view. Nevertheless, I never understood whether such a way of thinking is the result of the current level of development of computing technologies. But the works of Leibniz prove that even without advances in modern technology, such an attitude to things is possible. Of course, it cannot be denied that the surrounding technologies and past experience impose restrictions on how far thought can go in its development.

Such thoughts lead us to a serious question - how much do we lack the technologies of the near future to advance in this way of thinking? This is a very serious question for me, but one thing I can say for sure. Throughout his life, Leibniz has seen only a few computers, and all they could do was simple arithmetic operations. Today, billions of computers around the world perform many different operations. And in the future, the number of computers will only increase ( Principle of Computational Equivalence) And no doubt we will reach a point where computers will surround us everywhere. As a result, we can program anything right up to atoms. Of course, similar successes have already been achieved in biology, but only to a limited extent. There will be no restrictions in the future.

To some extent, this will entail a combination of computing and physical processes. But presenting it is now as difficult as Leibniz to imagine Wolfram Mathematica or Wolfram | Alpha.

Leibniz died on November 14, 1716. In 2016, there will be 300 years from this day. And this will be a good reason to finally study his entire legacy and celebrate the fact that many of his main ideas were brought to life 300 years later in a way that he could not imagine.