Neuroplasticity in artificial neural networks
 Hello, Habr, have not seen each other for a long time. In this post I would like to talk about such a relatively new concept in machine learning as transfer learning . Since I did not find any well-established translation of this term, the title of the post also contains a different but similar term, which seems to be a biological prerequisite for formalizing the theory of knowledge transfer from one model to another. So, the plan is this: first, consider the biological background; after we touch on the difference between transfer learning from a very similar idea of pre-training a deep neural network ; and in the end we discuss the real problem of semantic image hashing. To do this, we will not be shy and take a deep (19 layers) convolutional neural network of winners of the imagenet 2014 contestin the “localization and classification” section ( Visual Geometry Group , University of Oxford), we’ll do a little trepanation for it, extract some of the layers and use them for our purposes. Go.
Hello, Habr, have not seen each other for a long time. In this post I would like to talk about such a relatively new concept in machine learning as transfer learning . Since I did not find any well-established translation of this term, the title of the post also contains a different but similar term, which seems to be a biological prerequisite for formalizing the theory of knowledge transfer from one model to another. So, the plan is this: first, consider the biological background; after we touch on the difference between transfer learning from a very similar idea of pre-training a deep neural network ; and in the end we discuss the real problem of semantic image hashing. To do this, we will not be shy and take a deep (19 layers) convolutional neural network of winners of the imagenet 2014 contestin the “localization and classification” section ( Visual Geometry Group , University of Oxford), we’ll do a little trepanation for it, extract some of the layers and use them for our purposes. Go.Neuroplasticity
First, consider the definition. Neuroplasticity is the property of the brain to change under the influence of experience or after an injury. Changes include both the creation of synaptic connections and the creation of new neurons . Until relatively recently, until the 70s of the twentieth century, it was believed that part of the brain, in particular the neocortex (and this is just all motor skills, speech, thinking, etc.), remained static after a certain period of growing up, could only be adjusted the strength of connections between neurons. But later more detailed studies confirmed the presence of neuroplasticity of the brain as a whole. I suggest a look at a short video:
To really feel the power of our brain, let's take a look at the experiment of the neurophysiologist Paul Bach-y-Rita, whose work has greatly influenced the recognition of neuroplasticity by the scientific community. An important factor affecting the scientist’s motivation was the fact that his father was paralyzed. Together with his brother physicist, they were able to raise his father to his feet by the age of 68, which allowed him to even engage in extreme sports. Their history has shown that even at a late age, the human brain is capable of rehabilitation. But this is a completely different story, back to the 1969 experience. The goal was serious: to give blind people (even from birth) the opportunity to see. To do this, a dental chair was taken and refitted as follows: a television camera was placed next to the chair, and a manipulator was brought to the chair, which made it possible to change the scale and position of the camera. 400 stimulants were mounted in the back of the chair, which formed a grid: the image received from the camera was compressed to a size of 20 by 20; stimulants were located at a distance of 12 mm from each other. A small millimeter tip was attached to each stimulator, which vibrated in proportion to the current supplied to the solenoid located inside the stimulator.

Using an oscilloscope, it was possible to visualize the image created by the vibration of stimulants.

A year later, Paul developed a mobile version of his system:
1970s mobile visor
A man is like Mavrodi, but that is not him.


Nowadays, instead of tactile signal transmission, they use the “short” path through a more sensitive organ - the language. As they say in the articles, a few hours are enough to begin to perceive the image by the receptors of the tongue.
modern option
Do you think he eats noodles? But no, he looks with his tongue.


And it is not surprising that they try to monetize such a find :



And it is not surprising that they try to monetize such a find :

So how does it work? Speaking in simple language (not by biologists and neurophysiologists, but rather in the language of data analysis), neurons are trained to efficiently extract signs and draw conclusions on them. Replacing the familiar signal with some other , our neural network still extracts good low-level features (for example, computer vision, given below, these will be different gradient transitions or patterns) on layers that are close to the sensor (eye, tongue, ear, etc.). d.). The deeper layers try to extract higher-level attributes (wheel, window). And probably, if you look for the wheel from the car in the sound signal, most likely we will not find it. Unfortunately, we’ll not be able to see what signs neurons extract, but thanks to the article "Visualizing and Understanding Convolutional Networks "there is an opportunity to look at the low-level and high-level features extracted by a deep convolutional neural network. This, of course, is not a biological network, and perhaps everything in reality is not so. At the very least, it gives some intuitive understanding of the reasons that you can even see the receptor language.
in the big picture in the spoiler shown several signs of each layer and the convolution of the original image, which activate them. As you can see, the deeper, the less abstract becomes camping signs.
Visualization of features in a fully trained model
Each gray square corresponds to the visualization of the filter (which is used for convolution) or the weights of one neuron, and each color picture is that part of the original image that activates the corresponding neuron. For clarity, neurons within one layer are grouped into thematic groups.


It can be assumed that, replacing the sensors, our brain does not need to retrain all neurons completely, it is enough to retrain only those that extract high-level features - and the rest are already able to extract high-quality features. Practice shows that this is approximately what it is. It is unlikely that in a couple of hours of walking with a plate on the tongue, the brain manages to remove and then grow new synaptic connections, without losing the ability to feel the taste of food with the receptors of the tongue.
And now let's remember how the history of artificial neural networks began. In 1949, Donald Hebb published the book The Organization of Behavior , which describes the first principles of ANN training . It is worth noting that modern learning algorithms are not far from these principles.
- if adjacent neurons are activated synchronously , then the connection between them is enhanced ;
- if the adjacent neurons are activated asynchronously , then the connection between them weakens (in fact, Hebb did not have this rule, it was added as an addition later).
Nine years later, Frank Rosenblatt creates the first model for teaching with a teacher - the perceptron . The author of the first artificial neural network did not pursue the goal of creating a universal approximator. He was a neurophysiologist, and his task was to create a device that can be trained like a human. Just look at what journalists write about the perceptron. IMHO, this is lovely:
New York Time, July 8, 1958
...


...

At the perceptron, Hebb's training rules were implemented. As we can see, synaptic plasticity in the rules has already been taken into account to some extent. And in principle, online learning gives us some plasticity - a neural network can constantly retrain on a continuous data stream, and its forecasts in connection with this will change over time, constantly taking into account changes in the data. But there are no recommendations for other aspects of neuroplasticity, such as sensory substitution or neurogenesis. But this is not surprising, before the adoption of neuroplasticity, just over 20 years remain. Given the subsequent history of the ANN, scientists were not up to simulating neuroplasticity, the question was about the survival of the theory in principle. Only after the next renaissance of neural networks in the 2000s, thanks to people like Hinton, LeCun , Benggio and Schmidthuber , other scientists have the opportunity to comprehensively approach machine learning and come to the concept of transfer learning.
Transfer learning
Define the goals of transfer learning. The authors of the 2009 publication of the same name identify three main goals:
- higher start - improving the quality of training already at the initial iterations due to a more careful selection of the initial parameters of the model or some other a priori information;
- higher slope - acceleration of convergence of the learning algorithm;
- higher asymptote - improving the upper achievable quality limit.
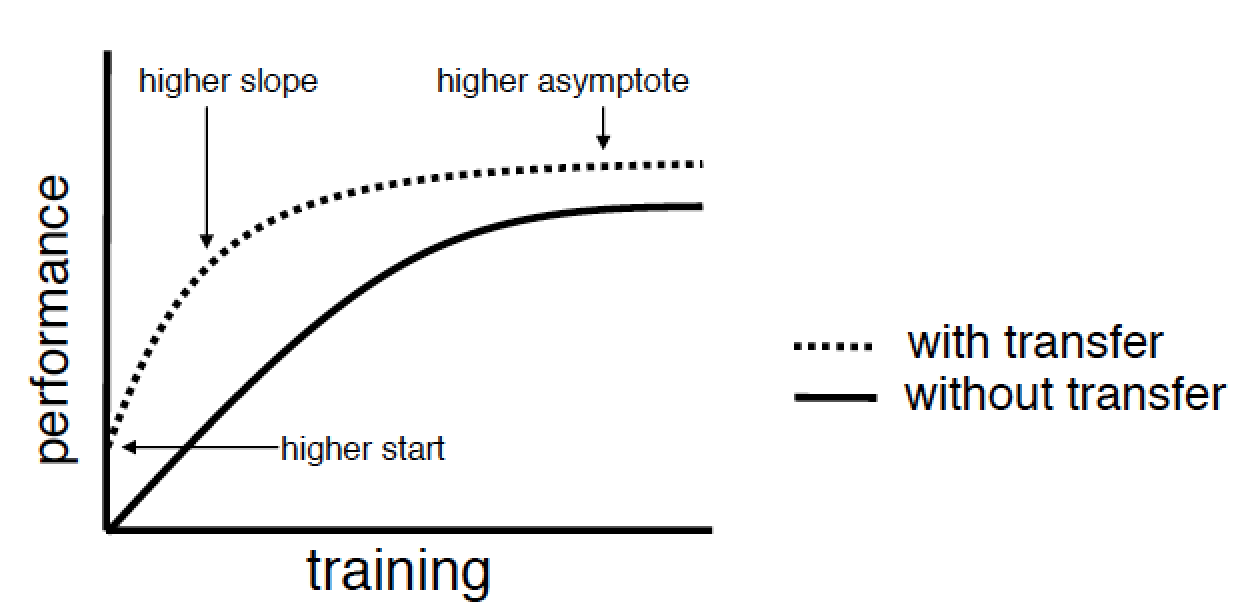
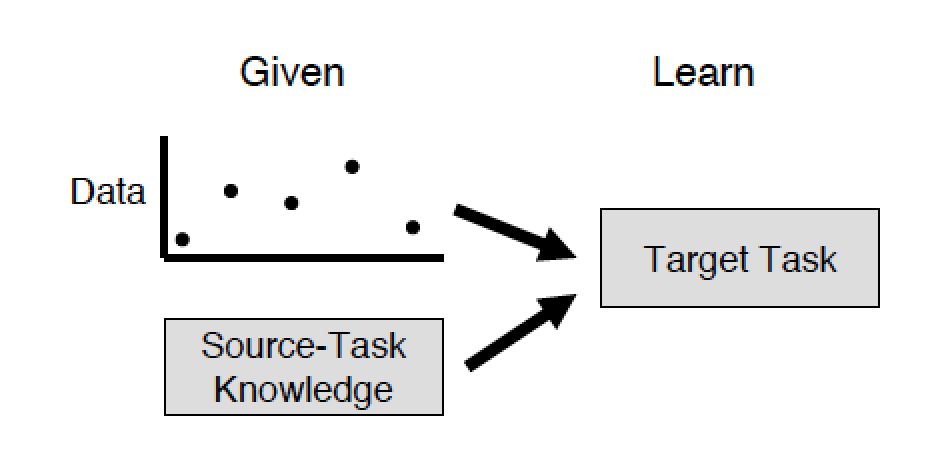
If you are familiar with deep network pre-trainingusing autoencoders or limited Boltzmann machines, you will immediately think: “So, it turns out I already practiced transfer learning, or at least I know how to do it.” But it turns out not. The authors draw a clear line between standard machine learning and transfer learning. In the standard approach, you only have a goal and a data set, and the task is to achieve this goal by any methods. As part of the solution to the problem, you can build a deep network, pre-train it with a greedy algorithm, build another dozen of them, and make an ensemble of them in some way. But all this will be within the framework of solving a single problem, and the time spent on solving such a problem will be comparable to the total time spent on training each model and its pre-training.
Now imagine that there are two tasks, and maybe even different people solved them. One of them uses part of the model of the other (source task) to reduce the time spent on creating a model from scratch and improve the performance of its model (target task). The process of transferring knowledge from one problem to another is transfer learning. And our brain probably does just that. As in the example above, its real task is to feel the taste with the receptors of the tongue and see with the eyes. The challenge arises - to perceive visual information with language receptors. And instead of growing new neurons or losing old weights and training them again, the brain just slightly adjusts the existing neural network to achieve a result.
Another feature of transfer learning is that information can only be transferred from the old model to the new one, because the old problem has long been solved. While in the standard approach, the different models involved in solving the problem can exchange information with each other.
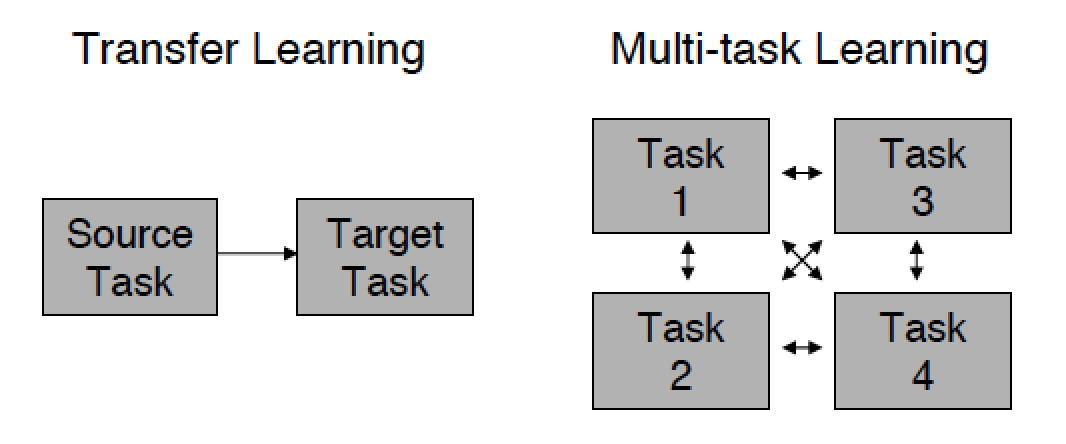
This post applies only to the part of transfer learning that relates to the task of teaching with a teacher, but for those who are interested I recommend reading the original. From there you will learn that, say, in learning with reinforcement or in training Bayesian networks, transfer learning began to be used earlier than in neural networks.
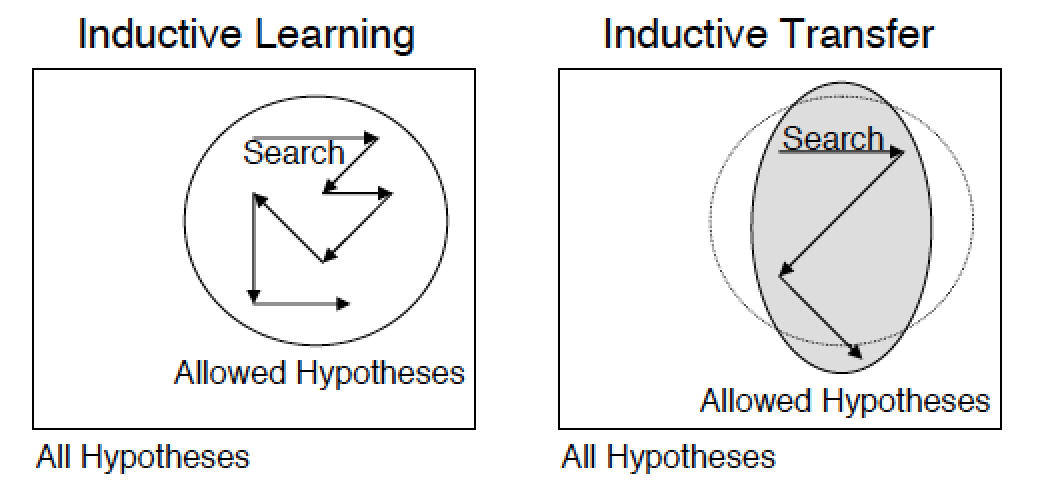
So, learning with a teacher is learning with labeled examples, while the learning process with examples is sometimes called inductive learning (moving from particular to general), and generalizing ability is called inductive bias . Hence the second name transfer learning - inductive transfer . Then we can say that the task of transferring knowledge in inductive training is to allow the knowledge accumulated during the training of the old model to affect the generalizing ability of the new model (even when solving another problem).
The transfer of knowledge can also be considered as some kind of regularization, which limits the search space to a certain set of acceptable and good hypotheses.
Practice
I hope that at this point you were imbued with such a seemingly unremarkable approach as the transfer of knowledge. After all, you can simply say that this is not a transfer of knowledge, neuroplasticity is far-fetched, and the best name for this method is copy-paste. Then you are just a pragmatist. This, of course, is also good, and then at least the third section you will like. Let's try to repeat something similar to that described in the first section, but on an artificial neural network.
To begin, we formulate the problem. Let's say you have a very large set of images. It is necessary to organize a search for similar images. Two problems arise here. Firstly, the measure of similarity between the images is not obvious, and if you just take the Euclidean distance from the n * m-dimensional vector, the result is not very satisfactory. Secondly, even if there is a quality measure, it will not allow us to avoid a full scan of the database, and the database may contain billions of images.
To solve this problem, you can use semantic hashing, one of such methods is described by Salakhudinova and Hinton in the article Semantic Hashing. Their idea is that the original data vector is encoded with a binary vector of small dimension (in our case, this is an image, and in the original article it is a binary vector of of words ). With this encoding, you can search for similar images in a linear time from the code length using the Hamming distance . Such encoding is called semantic, since images that are close in meaning and content (texts, music, etc.) in the new space of attributes are located close to each other. To implement this idea, they used a deep network of trust , the learning algorithm of which was developed by Hinton and the company back in 2006:
- the input network generally takes real values (gaussian-bernoulli rbm) and encodes them into a long binary vector, each next layer tries to reduce the length of the binary code (berboulli-bernoulli rbm);
- such a network is pre-trained sequentially from the bottom up by its own limited Boltzmann machine, where each next one uses the output of the previous one as its input data;
- then the network is deployed in the reverse order and is trained as a deep auto-encoder , which receives a slightly noisy vector at the input, and it tries to restore the original not-noisy image; this step is called fine turning;
- after all, the binary image in the middle of the autoencoder will be the desired binary hash from the input image.
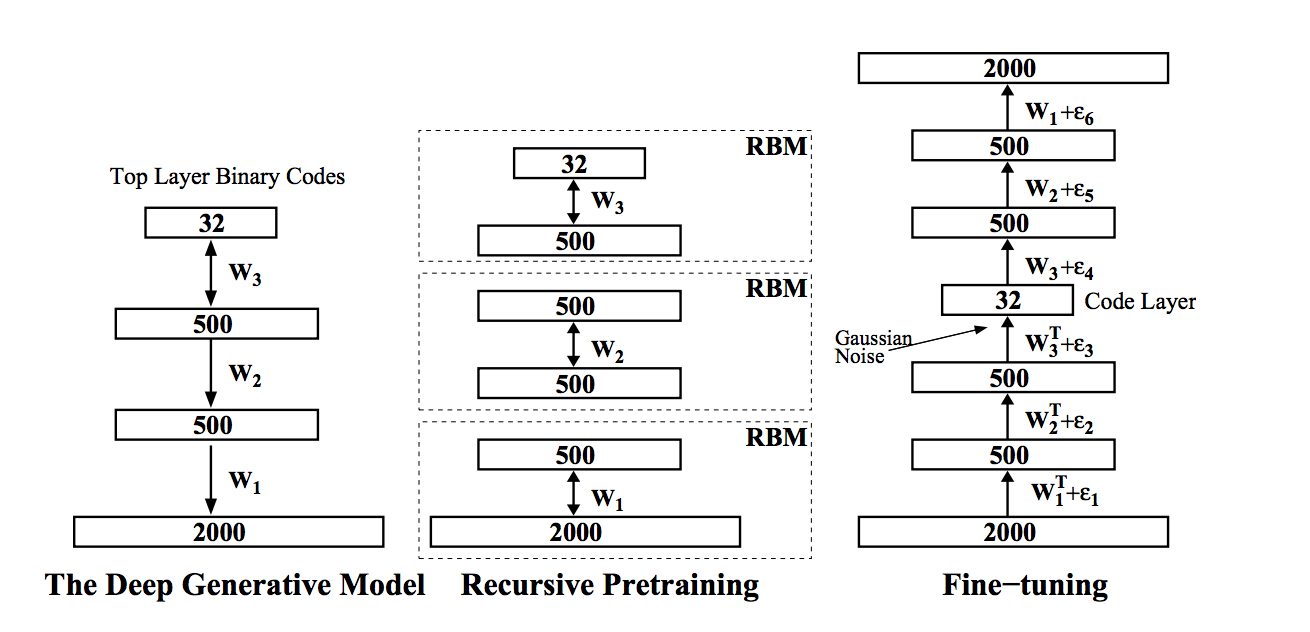
It seems to me that this is a brilliant model, and I decided that, in principle, the problem has been solved, thanks to Hinton. I started pre-training on the NVIDIA Tesla K20, waited a couple of days, and it turned out that everything was not as rosy as Hinton describes. Either because the pictures are large, or because I used gaussian-bernoulli rbm, and the article uses poisson-bernoulli rbm, or because of the specificity of the data, or maybe, in general, I did not teach much . But somehow I did not want to wait any longer. And then I remembered the advice of Maxim Milakov - use convolution networks, as well as the term transfer learning from one of his presentations. There were, of course, other options, ranging from compressing the dimension of pictures and quantifying colors, to classic signs of computer vision and combining them in bag of visual words. But once I entered the deep learning path, it’s not so easy to turn off it, and the bonuses that transfer learning promises (especially saving time) have deceived me.
It turned out that the VGG group mentioned at the beginning, which won ImageNet in 2014, laid out its trained neural network for free access for non-commercial use , so I downloaded it for research purposes only.
Generally, ImageNet- This is not only a competition, but also a database of images, which contains a little more than one million real images. Each image is assigned to one of 1000 classes. The set is balanced by class, that is, just over 1000 images per class. The Oxford guys won the Localization and Classification nomination. Since there can be more than one object in the images, the evaluation is based on whether the correct answer is in the top 5 most likely variants according to the model version. In the image below you can see an example of one of the models in the pictures from imagenet. Pay attention to a funny mistake with the Dalmatians, the model, unfortunately, did not find cherries there.

With such variability of the dataset, it is logical to assume that somewhere in the network there is an effective feature extractor, as well as a classifier that decides which class the image belongs to. I would like to get this very extractor, separate it from the classifier and use it to train a deep auto-encoder from an article on semantic hashing.
The VGG neural network is trained and saved in Caffe format . A very cool library for deep learning, and most importantly - easy to learn, I recommend that you familiarize yourself. Before you trepan the VGG network using caffe, I suggest a quick glance at the network itself. If the details are interesting, then I recommend the original article - Very Deep Convolutional Networks for Large-Scale Image Recognition(the name already hints at the depth of the network). And for those who are not familiar with convolution networks at all, you must at least read the Russian Wikipedia before moving on, it will not take more than 5-10 minutes (or there is a small description on Habré ).
So, for the article and the competition, the authors trained several models:
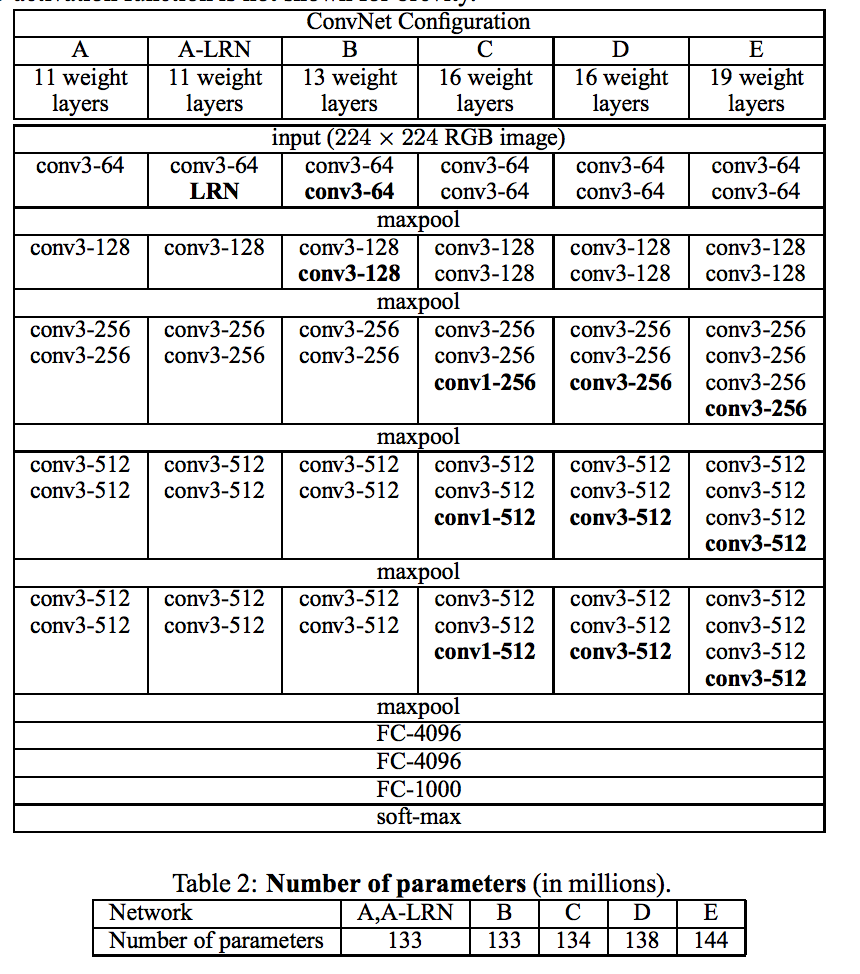
On their page, they posted options D and E. For the experiment, we will take the 19-layer version of E, in which the first 16 layers are convolutional, and the last three are fully connected. The last three layers are sensitive to the size of the images, so for the experiment, without thinking twice, I threw them out and left the first 16 layers, considering that I deleted the high-level signs.
The caffe library uses Google to describe the models.Protocol Buffers , and a full description of the network is as follows.
19-layer model
name: "VGG_ILSVRC_19_layers"
input: "data"
input_dim: 10
input_dim: 3
input_dim: 224
input_dim: 224
layers {
bottom: "data"
top: "conv1_1"
name: "conv1_1"
type: CONVOLUTION
convolution_param {
num_output: 64
pad: 1
kernel_size: 3
}
}
layers {
bottom: "conv1_1"
top: "conv1_1"
name: "relu1_1"
type: RELU
}
layers {
bottom: "conv1_1"
top: "conv1_2"
name: "conv1_2"
type: CONVOLUTION
convolution_param {
num_output: 64
pad: 1
kernel_size: 3
}
}
layers {
bottom: "conv1_2"
top: "conv1_2"
name: "relu1_2"
type: RELU
}
layers {
bottom: "conv1_2"
top: "pool1"
name: "pool1"
type: POOLING
pooling_param {
pool: MAX
kernel_size: 2
stride: 2
}
}
layers {
bottom: "pool1"
top: "conv2_1"
name: "conv2_1"
type: CONVOLUTION
convolution_param {
num_output: 128
pad: 1
kernel_size: 3
}
}
layers {
bottom: "conv2_1"
top: "conv2_1"
name: "relu2_1"
type: RELU
}
layers {
bottom: "conv2_1"
top: "conv2_2"
name: "conv2_2"
type: CONVOLUTION
convolution_param {
num_output: 128
pad: 1
kernel_size: 3
}
}
layers {
bottom: "conv2_2"
top: "conv2_2"
name: "relu2_2"
type: RELU
}
layers {
bottom: "conv2_2"
top: "pool2"
name: "pool2"
type: POOLING
pooling_param {
pool: MAX
kernel_size: 2
stride: 2
}
}
layers {
bottom: "pool2"
top: "conv3_1"
name: "conv3_1"
type: CONVOLUTION
convolution_param {
num_output: 256
pad: 1
kernel_size: 3
}
}
layers {
bottom: "conv3_1"
top: "conv3_1"
name: "relu3_1"
type: RELU
}
layers {
bottom: "conv3_1"
top: "conv3_2"
name: "conv3_2"
type: CONVOLUTION
convolution_param {
num_output: 256
pad: 1
kernel_size: 3
}
}
layers {
bottom: "conv3_2"
top: "conv3_2"
name: "relu3_2"
type: RELU
}
layers {
bottom: "conv3_2"
top: "conv3_3"
name: "conv3_3"
type: CONVOLUTION
convolution_param {
num_output: 256
pad: 1
kernel_size: 3
}
}
layers {
bottom: "conv3_3"
top: "conv3_3"
name: "relu3_3"
type: RELU
}
layers {
bottom: "conv3_3"
top: "conv3_4"
name: "conv3_4"
type: CONVOLUTION
convolution_param {
num_output: 256
pad: 1
kernel_size: 3
}
}
layers {
bottom: "conv3_4"
top: "conv3_4"
name: "relu3_4"
type: RELU
}
layers {
bottom: "conv3_4"
top: "pool3"
name: "pool3"
type: POOLING
pooling_param {
pool: MAX
kernel_size: 2
stride: 2
}
}
layers {
bottom: "pool3"
top: "conv4_1"
name: "conv4_1"
type: CONVOLUTION
convolution_param {
num_output: 512
pad: 1
kernel_size: 3
}
}
layers {
bottom: "conv4_1"
top: "conv4_1"
name: "relu4_1"
type: RELU
}
layers {
bottom: "conv4_1"
top: "conv4_2"
name: "conv4_2"
type: CONVOLUTION
convolution_param {
num_output: 512
pad: 1
kernel_size: 3
}
}
layers {
bottom: "conv4_2"
top: "conv4_2"
name: "relu4_2"
type: RELU
}
layers {
bottom: "conv4_2"
top: "conv4_3"
name: "conv4_3"
type: CONVOLUTION
convolution_param {
num_output: 512
pad: 1
kernel_size: 3
}
}
layers {
bottom: "conv4_3"
top: "conv4_3"
name: "relu4_3"
type: RELU
}
layers {
bottom: "conv4_3"
top: "conv4_4"
name: "conv4_4"
type: CONVOLUTION
convolution_param {
num_output: 512
pad: 1
kernel_size: 3
}
}
layers {
bottom: "conv4_4"
top: "conv4_4"
name: "relu4_4"
type: RELU
}
layers {
bottom: "conv4_4"
top: "pool4"
name: "pool4"
type: POOLING
pooling_param {
pool: MAX
kernel_size: 2
stride: 2
}
}
layers {
bottom: "pool4"
top: "conv5_1"
name: "conv5_1"
type: CONVOLUTION
convolution_param {
num_output: 512
pad: 1
kernel_size: 3
}
}
layers {
bottom: "conv5_1"
top: "conv5_1"
name: "relu5_1"
type: RELU
}
layers {
bottom: "conv5_1"
top: "conv5_2"
name: "conv5_2"
type: CONVOLUTION
convolution_param {
num_output: 512
pad: 1
kernel_size: 3
}
}
layers {
bottom: "conv5_2"
top: "conv5_2"
name: "relu5_2"
type: RELU
}
layers {
bottom: "conv5_2"
top: "conv5_3"
name: "conv5_3"
type: CONVOLUTION
convolution_param {
num_output: 512
pad: 1
kernel_size: 3
}
}
layers {
bottom: "conv5_3"
top: "conv5_3"
name: "relu5_3"
type: RELU
}
layers {
bottom: "conv5_3"
top: "conv5_4"
name: "conv5_4"
type: CONVOLUTION
convolution_param {
num_output: 512
pad: 1
kernel_size: 3
}
}
layers {
bottom: "conv5_4"
top: "conv5_4"
name: "relu5_4"
type: RELU
}
layers {
bottom: "conv5_4"
top: "pool5"
name: "pool5"
type: POOLING
pooling_param {
pool: MAX
kernel_size: 2
stride: 2
}
}
layers {
bottom: "pool5"
top: "fc6"
name: "fc6"
type: INNER_PRODUCT
inner_product_param {
num_output: 4096
}
}
layers {
bottom: "fc6"
top: "fc6"
name: "relu6"
type: RELU
}
layers {
bottom: "fc6"
top: "fc6"
name: "drop6"
type: DROPOUT
dropout_param {
dropout_ratio: 0.5
}
}
layers {
bottom: "fc6"
top: "fc7"
name: "fc7"
type: INNER_PRODUCT
inner_product_param {
num_output: 4096
}
}
layers {
bottom: "fc7"
top: "fc7"
name: "relu7"
type: RELU
}
layers {
bottom: "fc7"
top: "fc7"
name: "drop7"
type: DROPOUT
dropout_param {
dropout_ratio: 0.5
}
}
layers {
bottom: "fc7"
top: "fc8"
name: "fc8"
type: INNER_PRODUCT
inner_product_param {
num_output: 1000
}
}
layers {
bottom: "fc8"
top: "prob"
name: "prob"
type: SOFTMAX
}
In order to make the described trepanation, it is enough to remove all layers in the model description, starting from fc6 (full connected layer). But it is worth noting that then the network output will be unlimited from above, because the activation function is a rectified linear unit :
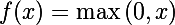
This question is conveniently solved by taking a sigmoidfrom the network outlet. We can hope that many neurons will be either 0 or some large number. Then, after taking the sigmoid, we get many units and 0.5 (the sigmoid from 0 is 0.5). If we normalize the obtained values in the range from 0 to 1, then they can be interpreted as the probabilities of activation of neurons, and almost all of them will be in the region of zero or one. The probability of neuron activation is interpreted as the probability of the presence of a sign in the image (for example, whether there is a human eye on it).
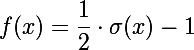
Here is a typical answer of such a network in my case:
normalized sigmoid from the last convolutional layer
0.0
0.0
0.0
0.0
0.0
0.0
1.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.994934
0.0
0.0
0.999047
0.829219
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.997255
0.0
0.0
0.0
0.0
0.0
0.0
0.0
1.0
1.0
0.0
0.999382
0.0
0.0
0.0
0.0
0.988762
0.0
0.0
1.0
1.0
0.0
1.0
1.0
0.0
1.0
1.0
1.0
1.0
1.0
0.0
1.0
1.0
0.0
0.0
1.0
1.0
0.0
1.0
1.0
0.0
0.0
0.0
0.0
0.0
0.847886
0.0
0.0
0.0
0.0
0.957379
0.0
0.0
0.0
0.0
0.0
1.0
0.999998
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
1.0
0.999999
0.0
0.54814
0.739735
0.0
0.0
0.0
0.912179
0.0
0.0
0.78984
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.681776
0.0
0.0
0.991501
0.0
0.999999
0.999152
0.0
0.0
1.0
0.0
0.0
0.0
0.0
0.999996
1.0
0.0
1.0
1.0
0.0
0.880588
0.0
0.0
0.0
0.0
0.0
0.0
0.836756
0.995515
0.0
0.999354
0.0
1.0
1.0
0.0
1.0
1.0
0.0
0.999897
0.0
0.953126
0.0
0.0
0.999857
0.0
0.0
0.937695
0.999983
1.0
0.0
0.0
0.0
0.0
0.0
1.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
1.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.994934
0.0
0.0
0.999047
0.829219
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.997255
0.0
0.0
0.0
0.0
0.0
0.0
0.0
1.0
1.0
0.0
0.999382
0.0
0.0
0.0
0.0
0.988762
0.0
0.0
1.0
1.0
0.0
1.0
1.0
0.0
1.0
1.0
1.0
1.0
1.0
0.0
1.0
1.0
0.0
0.0
1.0
1.0
0.0
1.0
1.0
0.0
0.0
0.0
0.0
0.0
0.847886
0.0
0.0
0.0
0.0
0.957379
0.0
0.0
0.0
0.0
0.0
1.0
0.999998
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
1.0
0.999999
0.0
0.54814
0.739735
0.0
0.0
0.0
0.912179
0.0
0.0
0.78984
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.681776
0.0
0.0
0.991501
0.0
0.999999
0.999152
0.0
0.0
1.0
0.0
0.0
0.0
0.0
0.999996
1.0
0.0
1.0
1.0
0.0
0.880588
0.0
0.0
0.0
0.0
0.0
0.0
0.836756
0.995515
0.0
0.999354
0.0
1.0
1.0
0.0
1.0
1.0
0.0
0.999897
0.0
0.953126
0.0
0.0
0.999857
0.0
0.0
0.937695
0.999983
1.0
0.0
0.0
0.0
0.0
0.0
1.0
0.0
0.0
0.0
In caffe, this issue is resolved as follows:
layers {
bottom: "pool5"
top: "sigmoid1"
name: "sigmoid1"
type: SIGMOID
}
Caffe implements a python wrapper, and the following code initializes the network and normalizes it:
caffe.set_mode_gpu()
net = caffe.Classifier('deploy.prototxt', 'VGG_ILSVRC_19_layers.caffemodel',
channel_swap=(2,1,0),
raw_scale=255,
image_dims=(options.width, options.height))
#..................
out = net.forward_all(**{net.inputs[0]: caffe_in})
out = out['sigmoid1'].reshape(out['sigmoid1'].shape[0], np.prod(out['sigmoid1'].shape[1:]))
out = (out - 0.5)/0.5
So, at the moment we have on our hands a binary (well, or almost) representation of images with high-dimensional vectors, in my case 4608, it remains to train the Deep Befief Network to compress these representations. The resulting model has become an even deeper network. Without waiting for DBN to learn for several days, let's conduct a search experiment: we will select a random image and search for it several nearest ones, in terms of Hamming distance. Note that this is all on raw features, on a vector of high dimension, without any weighting of signs.
Explanations: the first picture is a picture of a request, a random image from the database; the rest are closest to her.
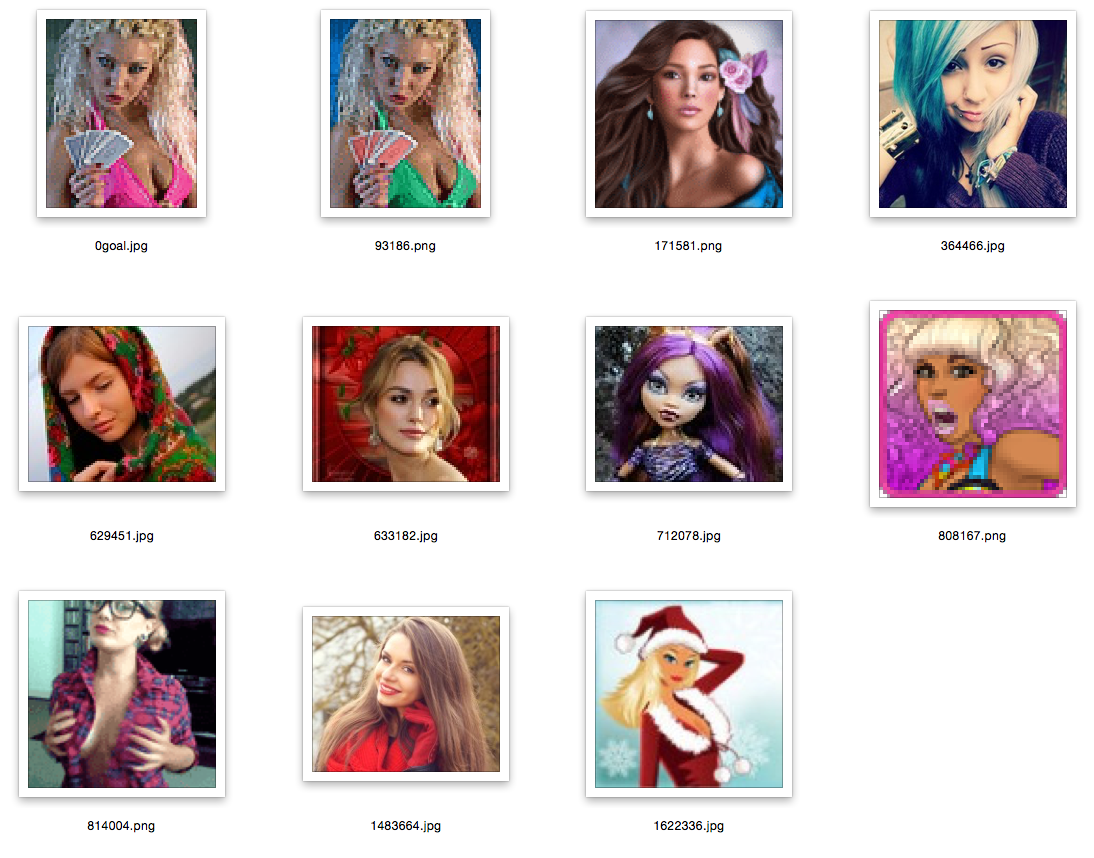
other examples in the spoiler
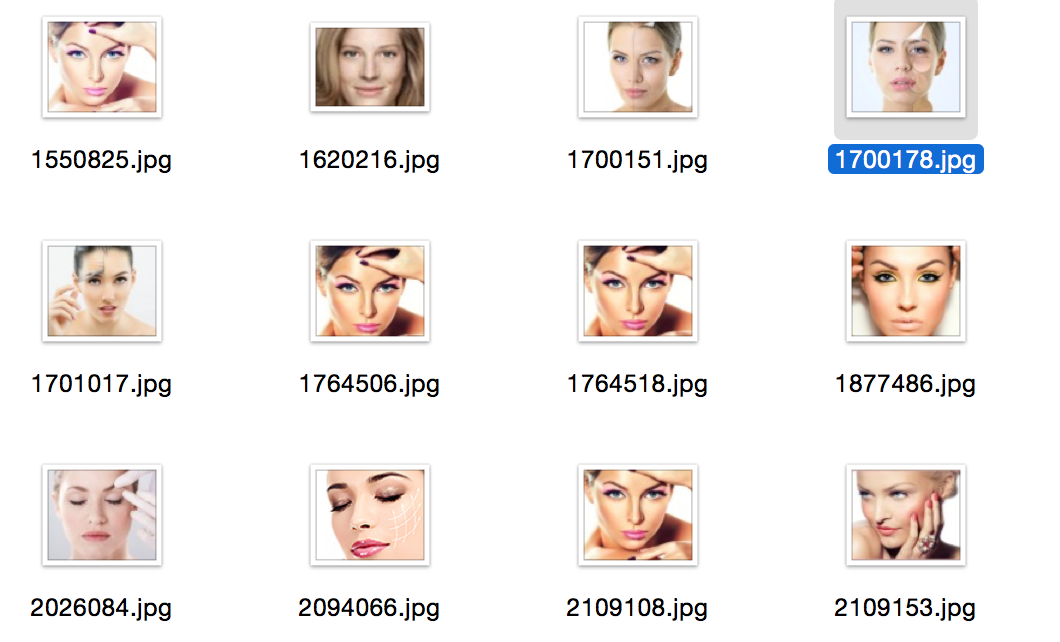
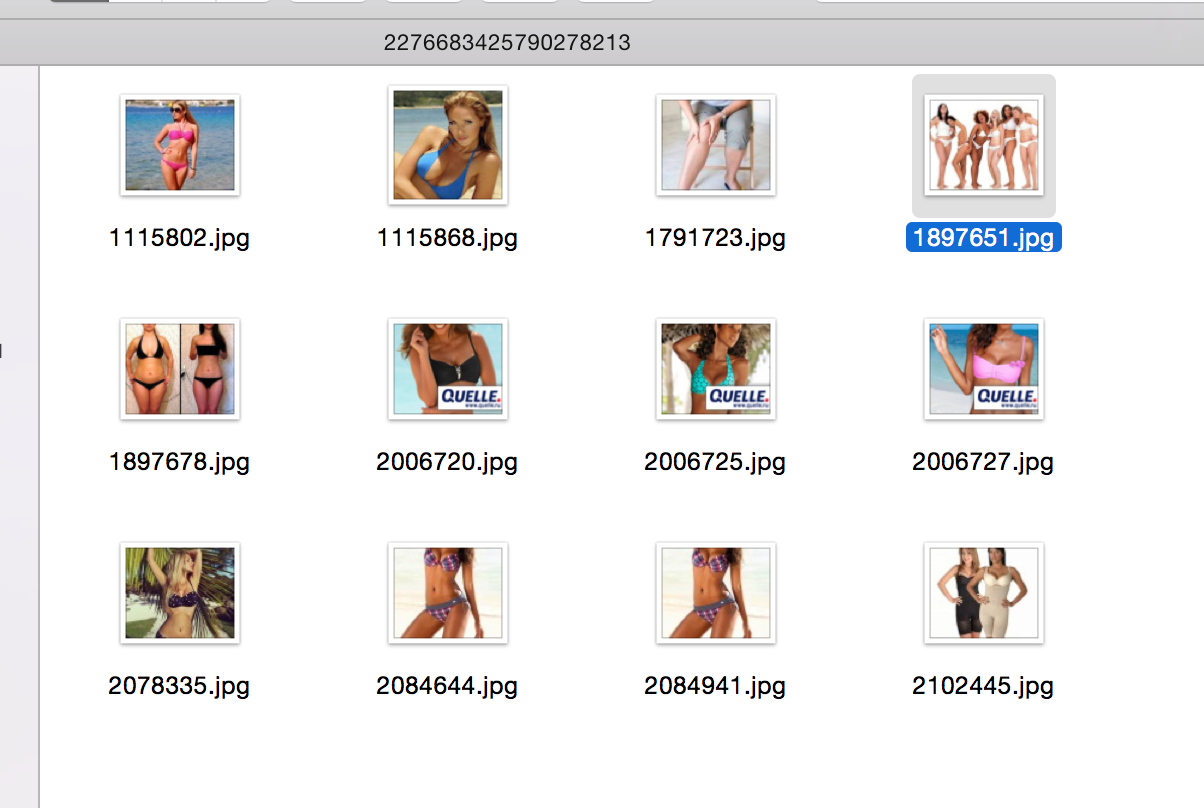
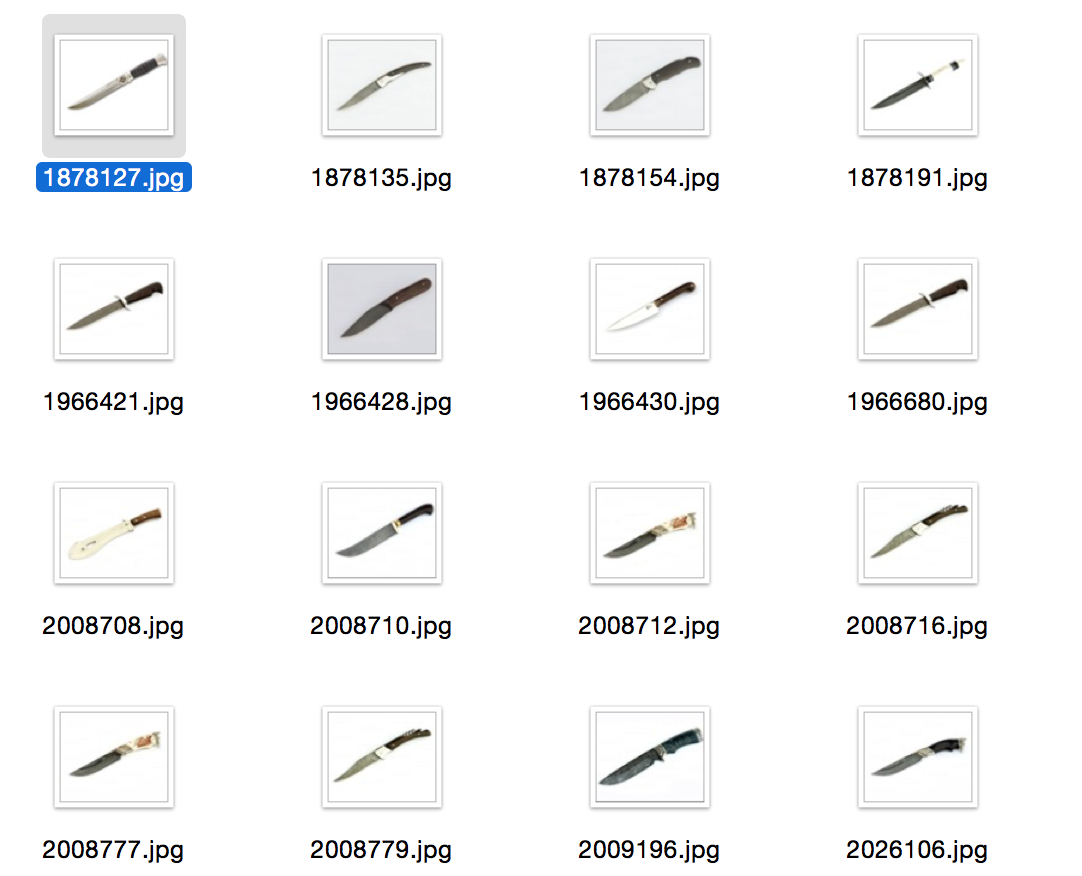
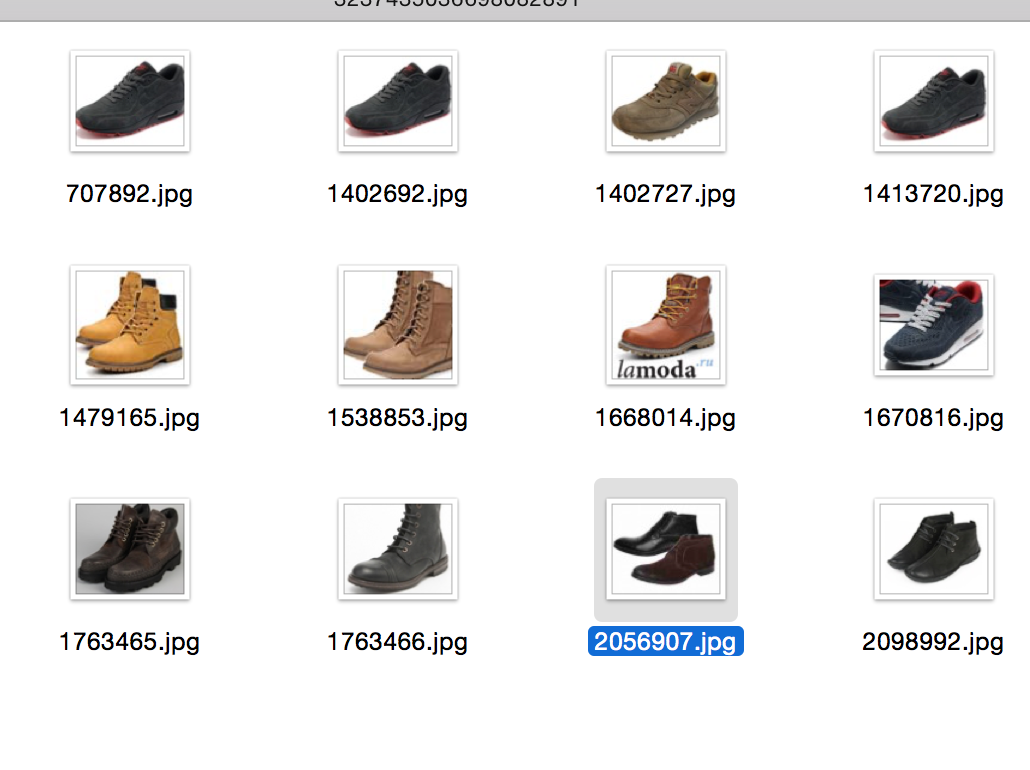

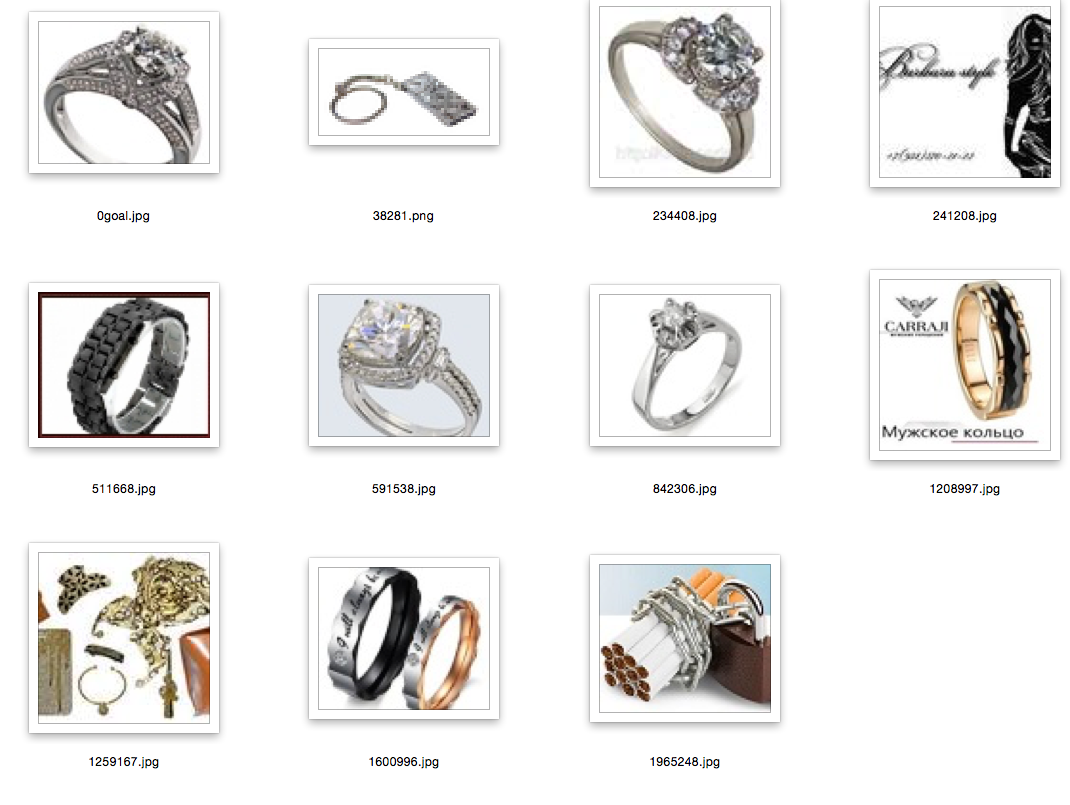
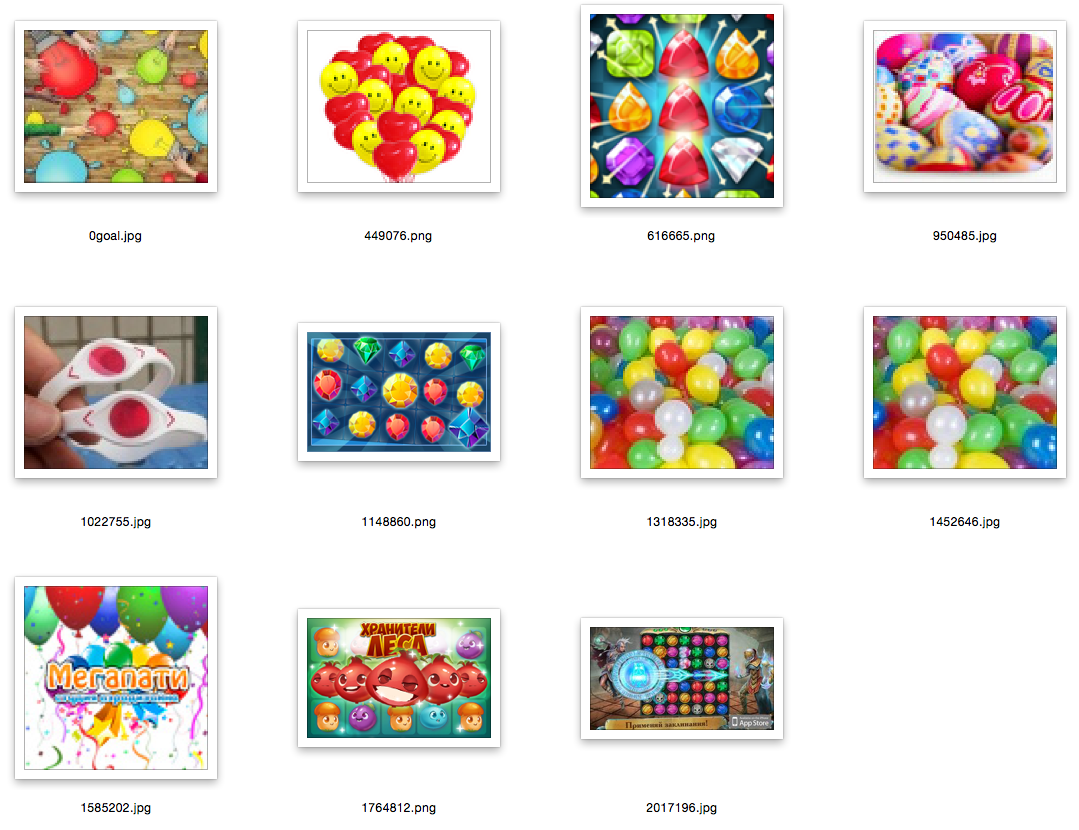

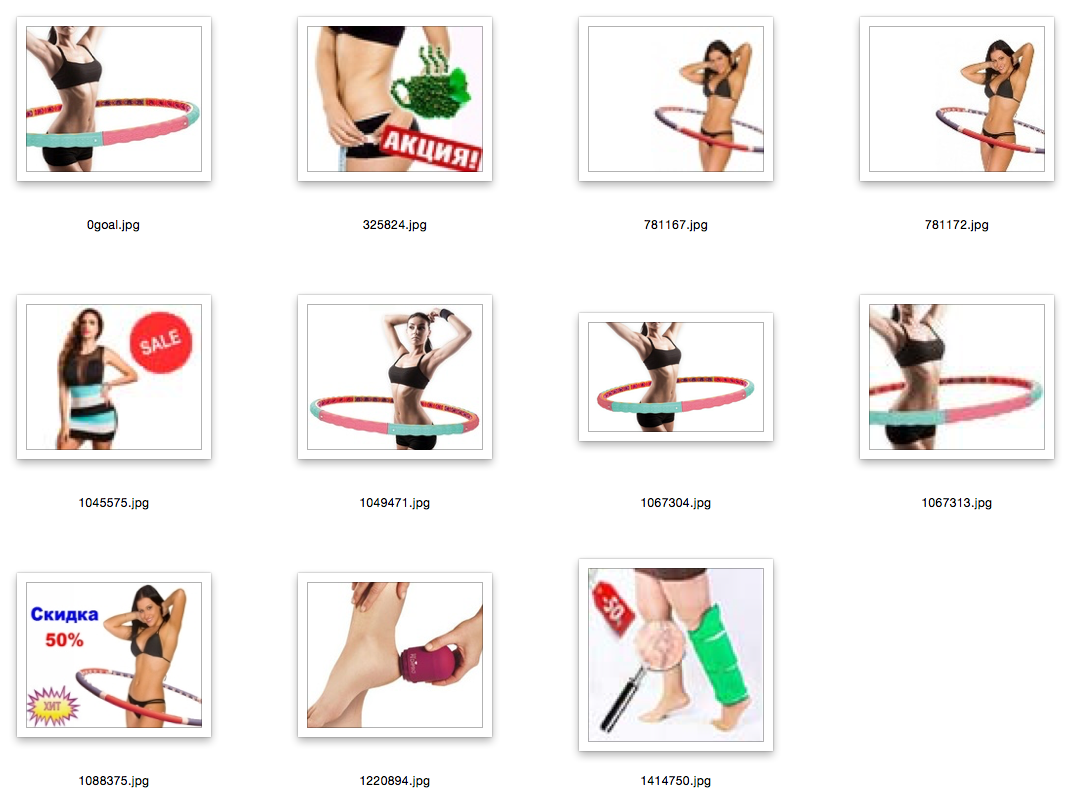











Conclusion and references
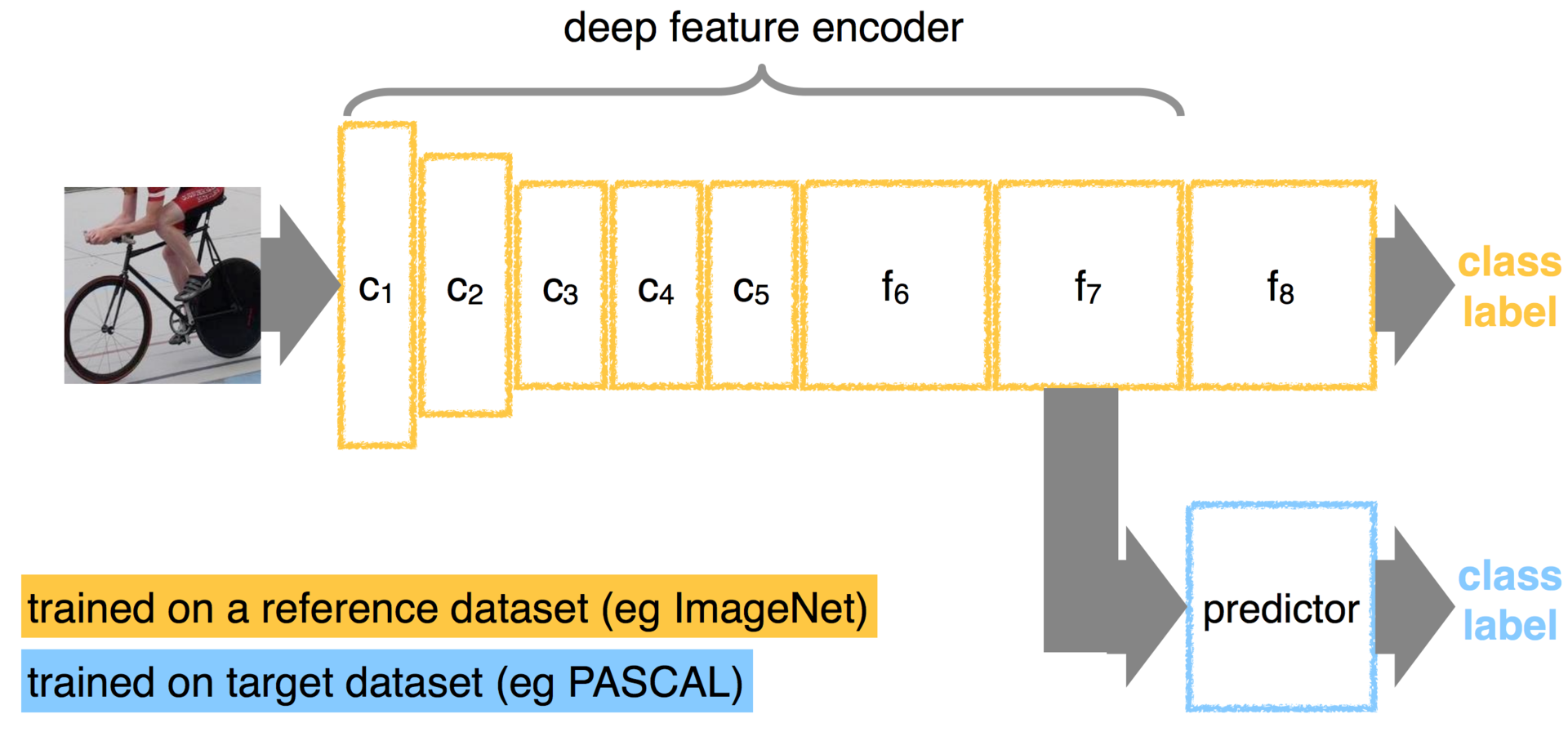
I think you can easily come up with an example in which you not only transfer static layers, but also train them in your own way. Let's say you can initialize part of your network using another network, and then retrain on your classes.
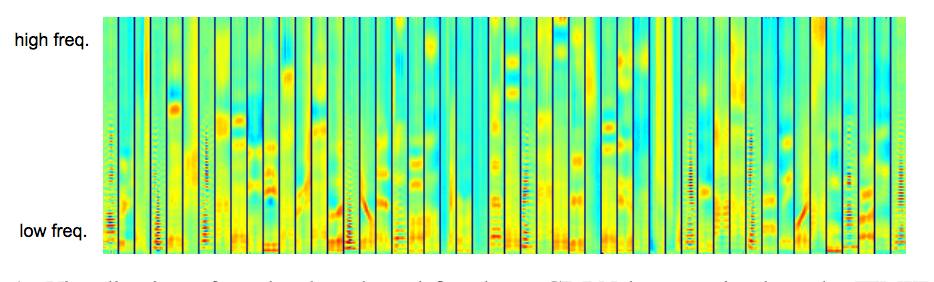
And if you try something closer to the experiment described in the first part? Please: here is an example article that uses convolutional deep belief networks to extract traits from audio signals. Why not use trained convolutions to initialize the cDBN weights? Why such a spectrogram is not an image, and why not use low-level features on it:
If you want to experiment with natural language processing and try transfer learning, here’s a suitable article by LeKunto start. And yes, there, too, the text is presented as an image.
In general, transfer learning is a great thing, and caffe is a cool library for deep learning.
There are many links in the text, I will give some of them here:
- Tongue vision
- Self-taught Learning: Transfer Learning from Unlabeled Data
- Transfer learning
- Large Scale Visual Recognition Challenge 2014 (ILSVRC2014)
- electricity for eyes
- Visualizing and Understanding Convolutional Networks
- Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion
- Semantic hashing
- Visual geometry group
- Very Deep Convolutional Networks for Large-Scale Visual Recognition (model)
- Caffe
- Very Deep Convolutional Networks for Large-Scale Visual Recognition (article)
- Image representations for large-scale visual recognition (A. Vedaldi from VGG)
