Error in the formula for checking the Delaunay condition
Introduction
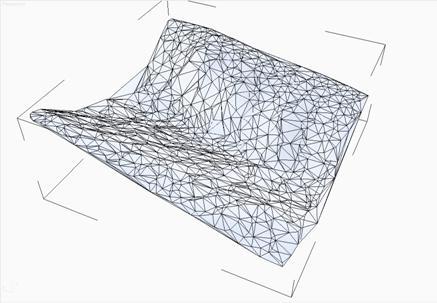
On an early Sunday morning, for the third day I was sitting at debugging a program for triangulating the result of a laser scan. A laser scan is a set of three-dimensional points. As a result of the program, you need to combine the points into disjoint polygons, thus creating a surface model. I recounted function after function on a piece of paper and, finally, I got to the function of verifying the fulfillment of the Delaunay condition . Apparently, the error was hidden somewhere in it. In a detailed analysis, it turned out that the formula indicated in a huge number of books about Delaunay triangulation does not always give the correct result. Details under the cut.
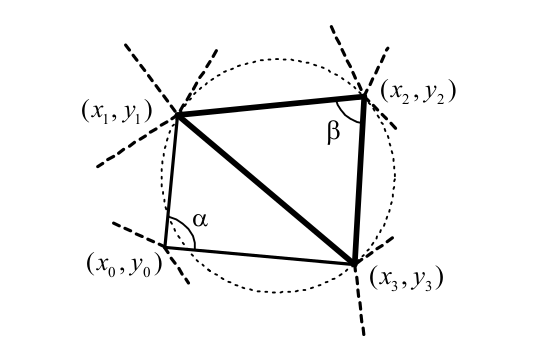
The Delaunay Condition
I will tell you briefly about the Delaunay condition itself. By the way, I got all the information from the wonderful book of A.V. Skvortsova "Delaunay triangulation and its application . " It is said that triangulation satisfies the Delaunay condition if none of the given triangulation points fall into the circle circumscribed around any constructed triangle. The fulfillment of this condition is necessary in order to maximize the sum of the minimum angles of all triangulation triangles. Simply put, so that triangles are not flattened.
The author offers 2 ways to check the Delaunay condition with the possibility of optimization for each of them.
The first method is the most obvious. He suggests calculating the center and radius of the circumscribed circle and directly checking the vertices of the neighboring triangles. As an optimization, it is proposed to store the calculated circumscribed circles in a triangle class. Not optimized verification requires 29 operations of multiplication and division and 24 operations of addition and subtraction. The complexity of the optimized check depends on the triangulation algorithm.
The second method is already more interesting. He argues that in order to check the conditions sufficient to allow for any adjacent triangle, the sum of opposite angles does not exceed the PI (
 ), which is equivalent to the condition
), which is equivalent to the condition  .
. 
Further, after reductions and transformations, a rather scary formula is obtained: The
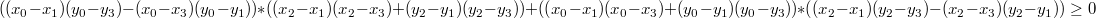
formula corresponds to the sine of the sum:
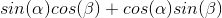 , where cosines and sines are expressed through the formulas of the scalar and pseudoscalar product, respectively. In the formulas, the product of the lengths of the vectors is omitted (apparently because it does not affect the sign of the expression).
, where cosines and sines are expressed through the formulas of the scalar and pseudoscalar product, respectively. In the formulas, the product of the lengths of the vectors is omitted (apparently because it does not affect the sign of the expression). As an optimization, it is proposed to first calculate the cosine signs. If
 and
and 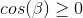 , then
, then 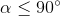 and
and  i.e. the Delaunay condition is satisfied. If
i.e. the Delaunay condition is satisfied. If  and
and  , then
, then 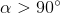 , and
, and  the condition is not satisfied. Otherwise, the full formula should be checked.
the condition is not satisfied. Otherwise, the full formula should be checked. Verification by full condition requires 10 operations of multiplication / division and 13 operations of addition / subtraction. The optimized verification, according to the author of the book, requires approximately 7 operations of multiplication / division and 9 operations of addition / subtraction.
After reviewing this information, I made a logical conclusion that the latter method was more optimal than the others and began to use it. As they say, nothing portended trouble.
Underwater rocks
During debugging, I began to notice the inappropriate behavior of the function check function of the Delaunay condition. The problem turned out to be that the sine sign depends on the order of listing the vertices. Thus, due to the sine sign, the sign of the whole expression changes. Maybe I don’t understand something, I’ll be glad if someone corrects me.
The first and only way to correct the situation that occurred to me is to take the sine expression modulo. Thus, the sine shows only the magnitude of the angle, and not the direction of the sweep, which is to our advantage.
Conclusion
It is very surprising to me that this formula is indicated in a huge number of books. What does it mean not only Russian-language literature, here is a publication in which the same information is indicated.
I am not a great specialist in mathematics, so I expect from the community adequate criticism and suggestions. Ready for discussion.
Thanks for attention.
