Freedom to dependent variables
The first of April is known as a day about white backs and untied shoelaces. But at the university where I studied, this day is also considered the day of mathematics. Therefore, I decided in this habrastatia to collect some of my funny puzzles and stories related in some sense to mathematics.
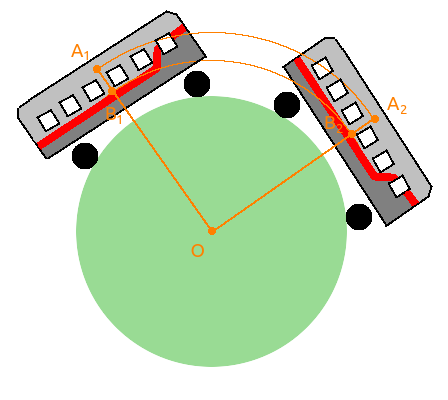
Imagine that the earth is a ball and we go with a friend from Omsk to Moscow along an arc of a circle, then my friend, who is traveling on the lower shelf, will travel a path equal to the length of the arc B 1 B 2 , and, I - the path equal to the length of the arc A 1 A 2 .
Between Omsk and Moscow about 2500 km, so the angle A 1 O A 2 is approximately 2500/6400 = 0.4 rad.
Since A 1 A 2 = OA 1 · 0.4, B 1 B 2 = OB 1· 0.4, and the distance between the upper and lower shelf is about 1 meter, then I will go to A 1 A 2 - B 1 B 2 = ( OA 1 - OB 1 ) · 0.4 = 1 · 0.4 m = 40 centimeters more for the same money.
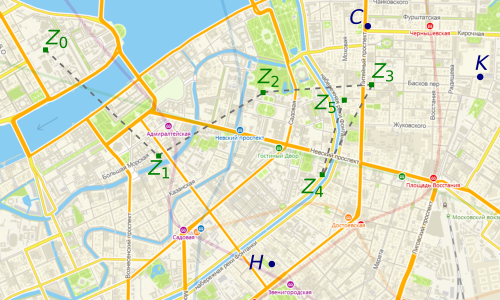
My friend Alexander made an appointment with three girls, whose name was Nastya, Sveta and Katya, on the same evening. He agreed to meet with Nastya near the house 90 k5 on the Fontanka River Embankment, with Sveta at the intersection of Liteiny and Kirochnaya, and with Katya at house 5 on Fontannaya Street (points N , C and K in the figure). Alexander left work to meet with Nastya, but halfway thought that Sveta was prettier, and went to the place of meeting with her. After half way to Sveta, he thought that he had more chances with Katya, and went to where they agreed to meet. But halfway through, he decided that Nastya was still smarter and went towards Nastya. Where did my friend end up if he continued to walk like this all evening?
Decision
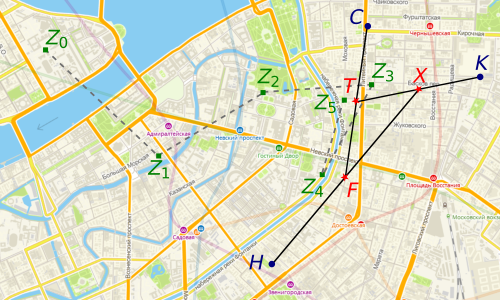
Suppose that Sanya is able to walk through walls and other obstacles. Place St. Petersburg on the complex plane and let it work in Z 0 . Then the sequence of points at which he changed the solutions has the form: Z 1 = ( Z 0 + H ) / 2, Z 2 = ( Z 1 + C ) / 2, Z 3 = ( Z 2 + K ) / 2, Z 4 = ( Z 3 + H ) / 2, ... We divide this sequence into three subsequences: Z 0, Z 3 , Z 6 , Z 9 , ...; Z 1 , Z 4 , Z 7 , Z 10 , ... and Z 2 , Z 5 , Z 8 , Z 11 , ... Let f ( Z ) = ((( Z + H ) / 2 + C ) / 2 + K ) / 2. Then the first subsequence is written in the form Z 0 , f ( Z 0), f ( f ( Z ( Z 0 )), f ( f ( f ( Z 0 ))), ... Note that the map f is contractive, therefore, by the Banach fixed point theorem, there exists a unique fixed point of this map, we denote it by X . Moreover, this subsequence converges to this point. For the other two subsequences, for similar reasons, there also exist fixed points, which we denote by F and Trespectively. These points correspond to the addresses: Nekrasov, 26, Rubinstein, 5 and Belinsky, 11 (see. Fig.). The first address is the Chronicles bar, the second is the Fiddler's Green bar, and the third is the Terminal. Thus, Alexander will spend the rest of the day in these bars, moving in turn from one to another.
If you go outside, you can see on the poles and walls of houses a lot of pieces of paper with pairs, the first element of which is a woman's name, and the second element is a sequence of numbers. Examples are given below.

Not at all interested in the second elements of these pairs, let us see what distribution the first elements have.
To do this, I once in August walked about six kilometers along the street and collected statistics.
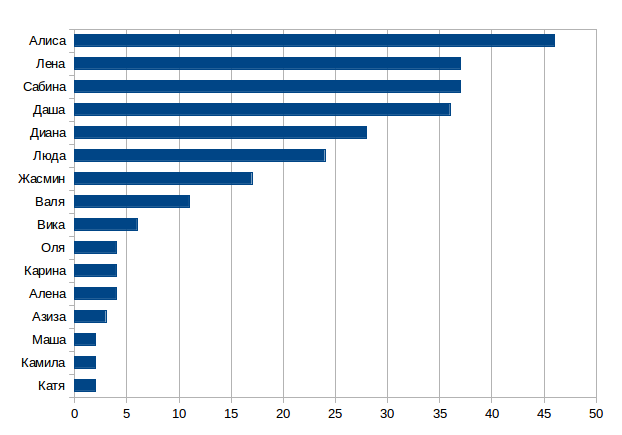
263 announcements were processed, TOP-5 names look like this: Alice, Lena, Sabina, Dasha, Diana:
My friend Konstantin leaves work every evening at 7 o'clock and goes to the subway. There, he accidentally selects a branch and direction, gets on a train, passes one station, then again randomly selects a branch and direction, again passes one station, and so on, until he gets home. Knowing that Kostya works for Leo Tolstoy, and lives near Art. m. Belyaevo, determine how often he drinks beer if he buys beer in a store near his house after work.
The decision to the
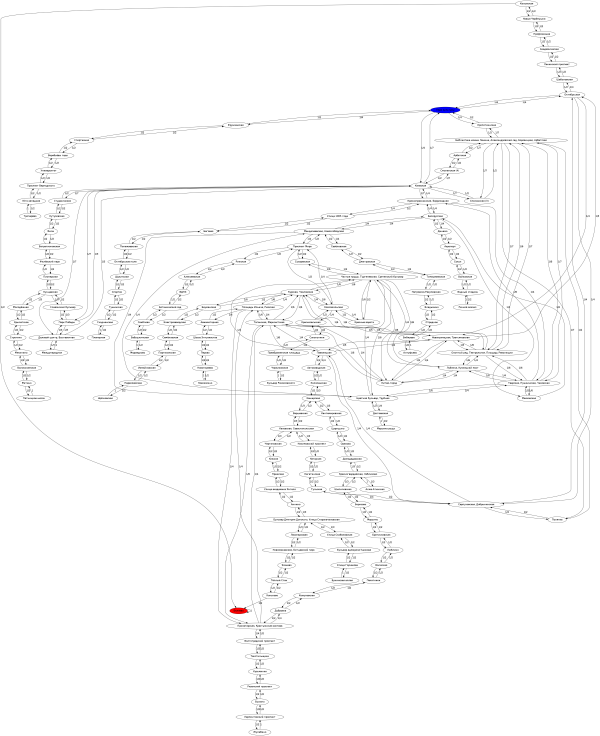
Moscow Metro can be compared the Markov chain with the matrix P (see. Fig.). And, since Kostya goes to the station. m. Belyaevo, then this state B will be absorbing. (Click on the image to enlarge.)
Further, suppose that it takes about three minutes to complete one haul. Since in Moscow they stop selling beer at 23:00, and (23:00 - 19:00) / 3 min. = 80, then we need to find the probability of being in state B in less than 80 steps. It is easy to understand that to find this probability, you need to raise the matrix P to the power of 79 and take the element at the intersection of the row that corresponds to the Culture Park and the column that corresponds to Belyaevo. Calculations show (see the figure below) that the desired probability is approximately 5.9%. Therefore, my friend drinks beer about once every 17 days.

Some time ago, a picture surfaced on the Internet with the fact that Chipsin Prings is a hyperbolic paraboloid:

When I saw her, I said to myself: “Aha! And since the hyperbolic paraboloid is a ruled surface, the chipsin should creep through a rectilinear slit. " Therefore, the next day I bought chips, cut a slot in the cardboard and did this experiment:

Another example of a ruled surface is a one-sheeted hyperboloid. You can check this fact with the help of the miracle yogurt bottle. We take a bottle from yogurt, cut out a part of the bottle that is something similar to a one-sheet hyperboloid, cut a gap in a sheet of cardboard again, insert a piece of the bottle into the slot and twist:

Have a good day!
1. Why I like to ride on the upper shelves in the train
Imagine that the earth is a ball and we go with a friend from Omsk to Moscow along an arc of a circle, then my friend, who is traveling on the lower shelf, will travel a path equal to the length of the arc B 1 B 2 , and, I - the path equal to the length of the arc A 1 A 2 .
Between Omsk and Moscow about 2500 km, so the angle A 1 O A 2 is approximately 2500/6400 = 0.4 rad.
Since A 1 A 2 = OA 1 · 0.4, B 1 B 2 = OB 1· 0.4, and the distance between the upper and lower shelf is about 1 meter, then I will go to A 1 A 2 - B 1 B 2 = ( OA 1 - OB 1 ) · 0.4 = 1 · 0.4 m = 40 centimeters more for the same money.

2. The task of my friend Sanya
My friend Alexander made an appointment with three girls, whose name was Nastya, Sveta and Katya, on the same evening. He agreed to meet with Nastya near the house 90 k5 on the Fontanka River Embankment, with Sveta at the intersection of Liteiny and Kirochnaya, and with Katya at house 5 on Fontannaya Street (points N , C and K in the figure). Alexander left work to meet with Nastya, but halfway thought that Sveta was prettier, and went to the place of meeting with her. After half way to Sveta, he thought that he had more chances with Katya, and went to where they agreed to meet. But halfway through, he decided that Nastya was still smarter and went towards Nastya. Where did my friend end up if he continued to walk like this all evening?

Decision
Suppose that Sanya is able to walk through walls and other obstacles. Place St. Petersburg on the complex plane and let it work in Z 0 . Then the sequence of points at which he changed the solutions has the form: Z 1 = ( Z 0 + H ) / 2, Z 2 = ( Z 1 + C ) / 2, Z 3 = ( Z 2 + K ) / 2, Z 4 = ( Z 3 + H ) / 2, ... We divide this sequence into three subsequences: Z 0, Z 3 , Z 6 , Z 9 , ...; Z 1 , Z 4 , Z 7 , Z 10 , ... and Z 2 , Z 5 , Z 8 , Z 11 , ... Let f ( Z ) = ((( Z + H ) / 2 + C ) / 2 + K ) / 2. Then the first subsequence is written in the form Z 0 , f ( Z 0), f ( f ( Z ( Z 0 )), f ( f ( f ( Z 0 ))), ... Note that the map f is contractive, therefore, by the Banach fixed point theorem, there exists a unique fixed point of this map, we denote it by X . Moreover, this subsequence converges to this point. For the other two subsequences, for similar reasons, there also exist fixed points, which we denote by F and Trespectively. These points correspond to the addresses: Nekrasov, 26, Rubinstein, 5 and Belinsky, 11 (see. Fig.). The first address is the Chronicles bar, the second is the Fiddler's Green bar, and the third is the Terminal. Thus, Alexander will spend the rest of the day in these bars, moving in turn from one to another.

3. Learning to see data everywhere
If you go outside, you can see on the poles and walls of houses a lot of pieces of paper with pairs, the first element of which is a woman's name, and the second element is a sequence of numbers. Examples are given below.

Not at all interested in the second elements of these pairs, let us see what distribution the first elements have.
To do this, I once in August walked about six kilometers along the street and collected statistics.
263 announcements were processed, TOP-5 names look like this: Alice, Lena, Sabina, Dasha, Diana:

4. The task of my friend Kostya
My friend Konstantin leaves work every evening at 7 o'clock and goes to the subway. There, he accidentally selects a branch and direction, gets on a train, passes one station, then again randomly selects a branch and direction, again passes one station, and so on, until he gets home. Knowing that Kostya works for Leo Tolstoy, and lives near Art. m. Belyaevo, determine how often he drinks beer if he buys beer in a store near his house after work.
The decision to the
Moscow Metro can be compared the Markov chain with the matrix P (see. Fig.). And, since Kostya goes to the station. m. Belyaevo, then this state B will be absorbing. (Click on the image to enlarge.)

Further, suppose that it takes about three minutes to complete one haul. Since in Moscow they stop selling beer at 23:00, and (23:00 - 19:00) / 3 min. = 80, then we need to find the probability of being in state B in less than 80 steps. It is easy to understand that to find this probability, you need to raise the matrix P to the power of 79 and take the element at the intersection of the row that corresponds to the Culture Park and the column that corresponds to Belyaevo. Calculations show (see the figure below) that the desired probability is approximately 5.9%. Therefore, my friend drinks beer about once every 17 days.

5. Chipsoids
Some time ago, a picture surfaced on the Internet with the fact that Chipsin Prings is a hyperbolic paraboloid:

When I saw her, I said to myself: “Aha! And since the hyperbolic paraboloid is a ruled surface, the chipsin should creep through a rectilinear slit. " Therefore, the next day I bought chips, cut a slot in the cardboard and did this experiment:

Another example of a ruled surface is a one-sheeted hyperboloid. You can check this fact with the help of the miracle yogurt bottle. We take a bottle from yogurt, cut out a part of the bottle that is something similar to a one-sheet hyperboloid, cut a gap in a sheet of cardboard again, insert a piece of the bottle into the slot and twist:

Have a good day!
