Lossless image compression
As I promised a post earlier , I present to you the second part of a large story about image compression. This time we will focus on lossless image compression methods.
The simplest algorithm to understand is the series length coding algorithm developed in the 1950s. The main idea of the algorithm is to represent each line of a binary image as a sequence of lengths of continuous groups of black and white pixels. For example, the second line of the image shown in Fig. 1 will look like this: 2,3,2. But in the decoding process, ambiguity will arise, because it is not clear which series: the first number encodes black or white. To solve this problem, there are two obvious methods: either first indicate the value of the first pixel for each line, or agree that for each line the length of the sequence of white pixels is indicated first (in this case, it can be zero).

The method of coding series lengths is very effective, especially for images with a simple structure, but this method can be significantly improved if the obtained sequences are additionally compressed by some entropy algorithm, for example, the Huffman method. In addition, the entropy algorithm can be independently applied separately for black and white sequences, which will further increase the degree of compression.
A further development of the idea of coding series lengths is the contour tracking compression method. This method is based on the use of high-level properties of the compressed image. Those. the image is perceived not just as a set of pixels, but as objects of the foreground and background. Compression is performed by efficiently representing objects. There are various ways of presentation, which we will consider later on the example of Fig. 2.

First of all, it should be noted that the description of each object should be enclosed in special messages (tags) of the beginning and end of the object. The first and easiest way is to specify the coordinates of the start and end points of the contour on each line. The image in Fig. 2 will be encoded as follows:
Of course, this record is further compressed using the algorithms considered earlier. But, again, the data can be converted in such a way as to increase the further degree of compression. For this, the so-called delta coding: instead of recording the immediate coordinates of the boundaries, their offset relative to the previous line is recorded. Using delta coding, the image in Fig. 2 will be encoded as follows:
The efficiency of delta coding is explained by the fact that the values of the displacements modulo close to zero and with a large number of objects in their description there will be many zero and close to zero values. Data converted in this way will be much better compressed by entropy algorithms.
Concluding the conversation about the compression of binary images, it is necessary to mention another method - coding of areas of persistence. In this method, the image is divided into a rectangle n 1 * n 2 pixels. All the resulting rectangles are divided into three groups: completely white, completely black and mixed. The most common category is encoded with a one-bit code word, and the other two categories receive two-bit codes. In this case, the code of the mixed region serves as a label, followed by n 1 * n 2bit describing the rectangle. If we break up the well-known image from Fig. 2 per square 2 * 2 pixels, you get five white squares, six black and 13 mixed. We agree 0 to denote the label of the mixed square, 11 - the label of the white square, and 10 - the label of the black square, the single white pixel will be encoded 1, and the black, respectively, 0. Then the whole image will be encoded as follows (bold marks):

As with most compression methods, the efficiency of this method is higher, the larger the original image. In addition, it can be noted that the values of mixed squares can be very efficiently compressed by dictionary algorithms.
This concludes the story about binary compression and goes on to the story of lossless compression of full-color and monochrome images.
There are many different approaches to lossless image compression. The most trivial ones come down to the direct application of the algorithms discussed earlier in the post ; other more advanced algorithms use information about the type of compressible data.
The first way that we look at will be a method known as coding for bit planes. Consider an arbitrary image with n brightness levels. Obviously, these levels can be represented using log 2 n bits. The method of decomposition into bit planes consists in dividing one image with n brightness levels into log 2 n binary images. In this case, the i-th image is obtained by extracting the i-th bits from each pixel of the original image. In Tab. 1 shows the decomposition of the original image on bit planes.
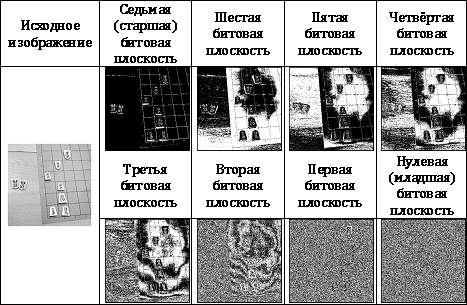
After the image is decomposed into bit planes, each resulting image can be compressed using the binary image compression methods discussed earlier.
A rather obvious drawback of this approach is the effect of multiple transfer of discharges with a slight change in brightness. For example, when changing the brightness from 127 to 128, the values of all binary digits (0111111 → 10000000) will change, which will cause a change in all bit planes.
To reduce the negative effects of multiple transfers, special codes are often used in practice, for example, Gray codes, in which two adjacent elements differ in only one category. To translate an n-bit number into a Gray code, it is necessary to perform a bitwise exclusive OR operation with the same number shifted by one bit to the right. The inverse transformation from the Gray code can be carried out by performing a bitwise exclusive OR operation for all non-zero offsets of the original number. The algorithms for converting to and from Gray code are shown in Listing 1.
It is easy to make sure that after conversion to the Gray code, when changing the brightness from 127 to 128, only one binary bit changes: The

bit planes obtained using the Gray code are more monotonous and, in general, better compressible. In Tab. 2 shows the bit planes obtained from the original image and the image converted to the Gray code:

Prediction coding is based on an idea similar to the delta coding algorithm. Most real images are locally homogeneous, i.e. the neighbors of a pixel have approximately the same brightness as the pixel itself. This condition is not satisfied at the boundaries of objects, but for most of the image it is true. Based on this, the pixel brightness value can be predicted based on the brightness of the neighbors. Of course, this prediction will not be absolutely accurate, and a prediction error will occur. It is this prediction error that is subsequently encoded using entropy algorithms. The coding efficiency is ensured by the already mentioned property of local homogeneity: in most of the image the value of the error modulo will be close to zero.
With this encoding method, it is very important that the same predictor is used for both encoding and decoding. In the general case, the predictor can use any characteristics of the image, but in practice, the predicted value is most often calculated as a linear combination of the brightnesses of neighbors: p k = ∑ i = 1 M α i * p k-i . In this formula, M is the number of neighbors participating in the prediction (prediction order), indices p are the numbers of pixels in the order in which they are viewed. It can be noted that with M = 1, prediction coding turns into the delta coding considered earlier (though, instead of the difference in coordinates, the brightness difference is now encoded).
Here it is necessary to discuss a little the order of viewing pixels. Up to this point, we assumed that pixels are viewed from left to right and from top to bottom, i.e. in the order of traversal by rows (Table 3):
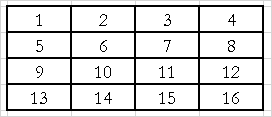
But it is obvious that the result of predicting the brightness of the fifth pixel based on the fourth (when traversing rows) will be very far from the true result. Therefore, in practice, other bypass orders are often used, for example, bypass lines with a spread, a snake, stripes, stripes with a spread, etc. Some of the listed workarounds are listed in Table. 4

Consider the described method with a specific example. Let's try to apply prediction coding for the image of the Ostankino television tower in Fig. 3

For simplicity, we will use first-order prediction (delta coding) and line-by-line traversal (each line will be encoded independently). In software implementation, it is necessary to decide how to transmit information about the first M pixels, the value of which cannot be predicted. The implementation of Listing 2 uses the following approach: the first pixel of each row is encoded directly by its brightness value, and all subsequent pixels in the row are predicted based on the previous one.
In Tab. 5 shows the result of this algorithm. Pixels predicted accurately are shown in white, and errors are marked in color, with a positive error value displayed in red and a negative value in green. The color intensity corresponds to the modulus of the error value.

Analysis shows that such an implementation provides an average prediction error of only 0.21 brightness levels. The use of higher-order predictions and other bypass methods can further reduce the prediction error, and hence increase the compression ratio.
Binary compression
Series Length Encoding Method
The simplest algorithm to understand is the series length coding algorithm developed in the 1950s. The main idea of the algorithm is to represent each line of a binary image as a sequence of lengths of continuous groups of black and white pixels. For example, the second line of the image shown in Fig. 1 will look like this: 2,3,2. But in the decoding process, ambiguity will arise, because it is not clear which series: the first number encodes black or white. To solve this problem, there are two obvious methods: either first indicate the value of the first pixel for each line, or agree that for each line the length of the sequence of white pixels is indicated first (in this case, it can be zero).

The method of coding series lengths is very effective, especially for images with a simple structure, but this method can be significantly improved if the obtained sequences are additionally compressed by some entropy algorithm, for example, the Huffman method. In addition, the entropy algorithm can be independently applied separately for black and white sequences, which will further increase the degree of compression.
Path Encoding Method
A further development of the idea of coding series lengths is the contour tracking compression method. This method is based on the use of high-level properties of the compressed image. Those. the image is perceived not just as a set of pixels, but as objects of the foreground and background. Compression is performed by efficiently representing objects. There are various ways of presentation, which we will consider later on the example of Fig. 2.

First of all, it should be noted that the description of each object should be enclosed in special messages (tags) of the beginning and end of the object. The first and easiest way is to specify the coordinates of the start and end points of the contour on each line. The image in Fig. 2 will be encoded as follows:
<START>
PAGE 2 4-8
PAGES 3 3-8
PAGES 4 3-8
<END>
<BEGIN>
PAGE 6 2-8
PAGES 7 2-9
PAGES 8 2-9
PAGES 9 2-9
<END>
Of course, this record is further compressed using the algorithms considered earlier. But, again, the data can be converted in such a way as to increase the further degree of compression. For this, the so-called delta coding: instead of recording the immediate coordinates of the boundaries, their offset relative to the previous line is recorded. Using delta coding, the image in Fig. 2 will be encoded as follows:
<START>
PAGE 2 4.8
pp. 3 -1.0
STR. 4 0.0
<END>
<START>
PAGE 6 2.8
STR. 7 0.1
STR. 8 0.0
STR. 9 0.0
<END>
The efficiency of delta coding is explained by the fact that the values of the displacements modulo close to zero and with a large number of objects in their description there will be many zero and close to zero values. Data converted in this way will be much better compressed by entropy algorithms.
Persistence Coding
Concluding the conversation about the compression of binary images, it is necessary to mention another method - coding of areas of persistence. In this method, the image is divided into a rectangle n 1 * n 2 pixels. All the resulting rectangles are divided into three groups: completely white, completely black and mixed. The most common category is encoded with a one-bit code word, and the other two categories receive two-bit codes. In this case, the code of the mixed region serves as a label, followed by n 1 * n 2bit describing the rectangle. If we break up the well-known image from Fig. 2 per square 2 * 2 pixels, you get five white squares, six black and 13 mixed. We agree 0 to denote the label of the mixed square, 11 - the label of the white square, and 10 - the label of the black square, the single white pixel will be encoded 1, and the black, respectively, 0. Then the whole image will be encoded as follows (bold marks):

As with most compression methods, the efficiency of this method is higher, the larger the original image. In addition, it can be noted that the values of mixed squares can be very efficiently compressed by dictionary algorithms.
This concludes the story about binary compression and goes on to the story of lossless compression of full-color and monochrome images.
Monochrome and full color compression
There are many different approaches to lossless image compression. The most trivial ones come down to the direct application of the algorithms discussed earlier in the post ; other more advanced algorithms use information about the type of compressible data.
Bit Plane Encoding
The first way that we look at will be a method known as coding for bit planes. Consider an arbitrary image with n brightness levels. Obviously, these levels can be represented using log 2 n bits. The method of decomposition into bit planes consists in dividing one image with n brightness levels into log 2 n binary images. In this case, the i-th image is obtained by extracting the i-th bits from each pixel of the original image. In Tab. 1 shows the decomposition of the original image on bit planes.

After the image is decomposed into bit planes, each resulting image can be compressed using the binary image compression methods discussed earlier.
A rather obvious drawback of this approach is the effect of multiple transfer of discharges with a slight change in brightness. For example, when changing the brightness from 127 to 128, the values of all binary digits (0111111 → 10000000) will change, which will cause a change in all bit planes.
To reduce the negative effects of multiple transfers, special codes are often used in practice, for example, Gray codes, in which two adjacent elements differ in only one category. To translate an n-bit number into a Gray code, it is necessary to perform a bitwise exclusive OR operation with the same number shifted by one bit to the right. The inverse transformation from the Gray code can be carried out by performing a bitwise exclusive OR operation for all non-zero offsets of the original number. The algorithms for converting to and from Gray code are shown in Listing 1.
function BinToGray (BinValue: byte): byte;
begin
BinToGray: = BinValue xor (BinValue shr 1);
end;
function GrayToBin (GrayValue: byte): byte;
var
BinValue: integer;
begin
BinValue: = 0;
while GrayValue> 0 do
begin
BinValue: = BinValue xor GrayValue;
GrayValue: = GrayValue shr 1;
end;
GrayToBin: = BinValue;
end;
It is easy to make sure that after conversion to the Gray code, when changing the brightness from 127 to 128, only one binary bit changes: The

bit planes obtained using the Gray code are more monotonous and, in general, better compressible. In Tab. 2 shows the bit planes obtained from the original image and the image converted to the Gray code:

Predictive coding
Prediction coding is based on an idea similar to the delta coding algorithm. Most real images are locally homogeneous, i.e. the neighbors of a pixel have approximately the same brightness as the pixel itself. This condition is not satisfied at the boundaries of objects, but for most of the image it is true. Based on this, the pixel brightness value can be predicted based on the brightness of the neighbors. Of course, this prediction will not be absolutely accurate, and a prediction error will occur. It is this prediction error that is subsequently encoded using entropy algorithms. The coding efficiency is ensured by the already mentioned property of local homogeneity: in most of the image the value of the error modulo will be close to zero.
With this encoding method, it is very important that the same predictor is used for both encoding and decoding. In the general case, the predictor can use any characteristics of the image, but in practice, the predicted value is most often calculated as a linear combination of the brightnesses of neighbors: p k = ∑ i = 1 M α i * p k-i . In this formula, M is the number of neighbors participating in the prediction (prediction order), indices p are the numbers of pixels in the order in which they are viewed. It can be noted that with M = 1, prediction coding turns into the delta coding considered earlier (though, instead of the difference in coordinates, the brightness difference is now encoded).
Here it is necessary to discuss a little the order of viewing pixels. Up to this point, we assumed that pixels are viewed from left to right and from top to bottom, i.e. in the order of traversal by rows (Table 3):

But it is obvious that the result of predicting the brightness of the fifth pixel based on the fourth (when traversing rows) will be very far from the true result. Therefore, in practice, other bypass orders are often used, for example, bypass lines with a spread, a snake, stripes, stripes with a spread, etc. Some of the listed workarounds are listed in Table. 4

Consider the described method with a specific example. Let's try to apply prediction coding for the image of the Ostankino television tower in Fig. 3

For simplicity, we will use first-order prediction (delta coding) and line-by-line traversal (each line will be encoded independently). In software implementation, it is necessary to decide how to transmit information about the first M pixels, the value of which cannot be predicted. The implementation of Listing 2 uses the following approach: the first pixel of each row is encoded directly by its brightness value, and all subsequent pixels in the row are predicted based on the previous one.
type
TPredictionEncodedImg = array of array of integer;
function DeltaEncoding: TPredictionEncodedImg;
var
r: TPredictionEncodedImg;
i, j: word;
begin
SetLength (r, GSI.N + 1);
for i: = 1 to GSI.N do
begin
SetLength (r [i], GSI.M + 1);
r [i, 1]: = GSI.i [i, 1];
end;
for i: = 1 to GSI.N do
for j: = 2 to GSI.M do
r [i, j]: = GSI.i [i, j] - GSI.i [i, j - 1];
DeltaEncoding: = r;
end;
In Tab. 5 shows the result of this algorithm. Pixels predicted accurately are shown in white, and errors are marked in color, with a positive error value displayed in red and a negative value in green. The color intensity corresponds to the modulus of the error value.

Analysis shows that such an implementation provides an average prediction error of only 0.21 brightness levels. The use of higher-order predictions and other bypass methods can further reduce the prediction error, and hence increase the compression ratio.
