Once upon a time, in a distant, distant galaxy (i.e. more than a year ago and outside of default city), one web programmer decided to write his Flash (it was not without megalomania, of course). The task then seemed difficult and very interesting. This article will discuss one of the problems that got in his way.
Those who painted in Flash know that in it shapes (filled areas) within the same layer never overlap, and lines are always drawn on top of filled shapes. In my opinion, this approach has a good plus - you have what you see in the image. However, when writing a vector editor, this leads to the need to solve the problem of correctly superimposing drawn objects (lines and filled shapes) on existing ones. Below I will try to show in stages how this can be done.




For simplicity, in what follows, I will call polygons filled areas bounded by straight lines and quadratic Bezier curves. As a rule, when referring to edges , I will mean visible drawn straight or curved lines (stroke lines).

Initial data

So, we have two images that we want to combine. Each is given by a set of edges and polygons.

Here's what we know about ribs:

• can be straight lines;
• can be bezier curves;

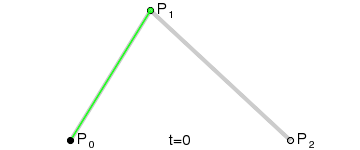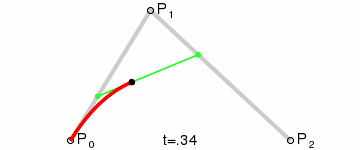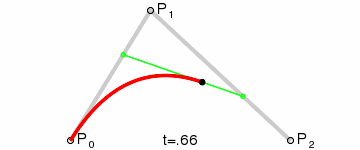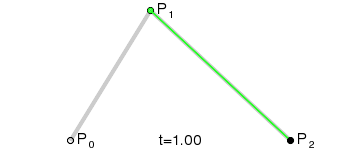  A quadratic Bezier curve is the simplest case when the curve has one control point and, in fact, is drawn inside a triangle defined by its three vertices. Great Wikipedia illustration:
• each rib has its own color;
• no two edges intersect (but can, of course, have a common start or end point);
• no two edges match.

So, in the figure on the right you can see 5 edges: two blue and three dark yellow.

And here is what we know about landfills:

• limited to straight or curved segments;
• never intersect;
• can adjoin each other, i.e. have a common border (in this case, the colors of the polygons should be different, or the border should be clearly highlighted by edges; thus, there should not be polygons that nothing prevents to merge into one);
• have their own fill option (in the simplest case, color);
• can be translucent (color can be specified with an alpha channel);
• may be non-convex;
• may have “holes” (ie, areas defined by straight / curved segments where there is no fill).

In light of the fact that the polygon is a complex object, we will describe it as a closed external contour + a set of internal disjoint contours that define holes.

Subtasks

It is clear that finding the union of two vector images is a difficult task, and therefore it is worth splitting it into several subtasks. That's what I did:

• search for intersections of all segments of one image with segments of another and the division of these segments by the found points;
• search for all contours (closed chains of segments) on the union of the segments of two images;
• determination of the presence / absence of a fill and its color for each path relative to each of the two images;
• removal of all edges of the original image that completely fell inside the shaded areas of the overlay image;
• removal from the source image of all polygons available in the overlay image without regard to color;
• adding to the edges and polygons of the original image all the edges and polygons of the overlay image (in this case, the matching edges of the original image are overwritten by the edges of the overlay);
• combining in the original image adjacent to each other polygons that have the same fill and do not have explicit separation by edges.

As a result of all these actions in the original image, we should get the desired result of the union.

I think it is clear that each of the subtasks is, at times, a non-trivial problem. Therefore, we consider them separately.

Search for the intersection of two segments

The segments we have are different, so we will consider three possible cases separately.

Both segments are straight

As you know, finding the intersection of two straight segments is not particularly difficult, you only need to remember that it is convenient to represent them in the parametric form in the calculations (formulas of the form y = kx + b have a fatal flaw: they quickly lose accuracy when the segment approaches the vertical position, and for vertical segments require separate consideration):

// M - точка на отрезке, S - начало отрезка, D - конец отрезка, t - значение из диапазона [0; 1]
M1 = S1 + (D1-S1) * t1 // параметрическое представление первого отрезка
M2 = S2 + (D2-S2) * t2 // параметрическое представление второго отрезка
// Пересечение - это когда M1 = M2 - получаем систему уравнений,
// из которой мы добудем значение t1:
Xs1 + (Xd1-Xs1) * t1 = Xs2 + (Xd2-Xs2) * t2
Ys1 + (Yd1-Ys1) * t1 = Ys2 + (Yd2-Ys2) * t2

I will not describe the output of t1 (I think everyone will cope here without much difficulty). After obtaining the value of t1, you need to make sure that it lies in the interval [0; 1] (otherwise the segments do not intersect), after which you can substitute it in the formula defining the first segment, thus obtaining the coordinates of the intersection point:

Xm = Xs1 + (Xd1-Xs1) * t1
Ym = Ys1 + (Yd1-Ys1) * t1

Bezier curve and straight line

The intersection of the Bezier curve and the straight segment is not so simple, but it can be solved analytically, especially if you guess first to rotate the segment and the curve so that the segment becomes strictly horizontal:

// P0, P1, P2 - точки, задающие кривую; t - значение из диапазона [0; 1]
M1 = (1-t1)^2 * P0 + 2*t1*(1-t1) * P1 + t1^2 * P2 // параметрическое представление кривой
// S - начало отрезка, D - конец
M2 = S + (D-S) * t2 // параметрическое представление прямого отрезка
// поворачиваем точки P0, P1, P2, S и D на угол a = -atan2(Yd-Ys, Xd-Xs);
// ниже расположены известные формулы для такого поворота
// (точка, заданная координатами (X, Y) переходит в точку (Xn, Yn))
Xn = X*cos(a) - Y*sin(a) 
Yn = X*sin(a) + Y*cos(a)

// формула кривой не изменилась (изменились только значения P0, P1 и P2)
Xm1 = (1-t1)^2 * Xp0 + 2*t1*(1-t1) * Xp1 + t1^2 * Xp2
Ym1 = (1-t1)^2 * Yp0 + 2*t1*(1-t1) * Yp1 + t1^2 * Yp2
// формула прямого отрезка упростилась для координаты Y:
Xm2 = Xs + (Xd-Xs) * t2
Ym2 = Ys // т.к. после поворота у нас Ys = Yd
// M1 = M2, т.е.
Xm1 = Xm2
Ym1 = Ym2
// достаточно рассмотреть только формулу для Y, т.к. именно там имеется упрощение:
(1-t1)^2*Yp0 + 2*t1*(1-t1)*Yp1 + t1^2*Yp2 = Ys

Solving this quadratic equation, we find the values ​​of t1 (and there can be two). For each value of t1, as in the case of straight segments, it is worth making sure that it lies within [0; 1]. Substituting the values ​​of t1 into the initial (before turning) formula of the curve, we obtain the coordinates of the desired intersection points.

Two Bezier curves

Analytically calculating the intersection points of two quadratic Bezier curves (and there can be up to 4 such points) is very difficult: the complexity is so high that even MathCAD gets indignant, reporting too long formulas. Also, as far as I understand the situation, in this case you have to work with complex numbers. Fortunately, there are numerical iterative methods for obtaining the intersection points of arbitrary curves with a given accuracy. Everything is simple here:

1. if the segments under consideration have a size less than the specified accuracy, we approximate them by straight lines and consider their intersection;
2. if at least one of the segments is more accurate, we beat it into two (more or less equal) parts and recursively apply the algorithm for the obtained segments.

Here you can enter optimization: first check whether the segments can basically intersect (for example, using bounding rectangles) and if not, then stop the current recursion branch.


The moment that may cause difficulty is the splitting of the Bezier curve into two parts (i.e., calculating new control points; determining the end point of the first curve that coincides with the starting point of the second curve is easy by substituting t = 0.5 in the formula of the curve). As it turned out, for this it is enough to calculate the coordinates of the centers of the segments defining the support triangle — the obtained points will be the control points for the new curves. The figure on the left illustrates the solution: the curve (P0, P1, P2) is divided into two curves, the support triangle of the first of them (P0, P1 ', P2') is highlighted in blue. The control point of the second curve (P2 ', ..., P2) is calculated in exactly the same way.

To be continued…