Finding the Best Sequence to Watch a List of the Top 250 Films Using the Wolfram Language (Mathematica)

Download the translation in the form of a Mathematica document, which contains all the code used in the article, here (archive, ~ 76 MB).

Introduction

Some time ago, to be precise - 515 days, Matthias Odisio published a post entitled “ Random and Optimal Mathematica Walks on IMDb's Top Films ” ( Mathematica random and optimal walks on the list of 250 best films according to IMDB). It talks about how you can get the optimal sequence of watching movies from the corresponding list , based on the proximity of movie genres and the proximity of movie posters in terms of color.

In [1]: =



Out [1] =



The idea of ​​this post seemed quite interesting to me, but I wanted to expand and deepen it significantly, following a few ideas:

• To build a more advanced function that evaluates the proximity of films, since it seems to me that building the distance function between films based on the proximity of movie posters based on the colors and genres of films used in them is not objective enough. It seems reasonable to me to construct the function of the distance between films on the basis of several factors: film genres, film descriptions, cast, director (s), year of production, screenwriter (s), etc.

• Matthias’s article used only Wolfram | Alpha data , which certainly simplifies the task and compacts the code. I would like to talk about how you can use data taken from anywhere in calculations, for example, obtained using web parsing from Wikipedia pages, loaded from text databases, etc.

I will not talk in this article about how to build the optimal sequence of viewing the list of 250 best films of KinoPoisk for the reason that I just do not want to have problems with the terms of use of this resource, which are pretty clear (see paragraph 6), that simply taking their list of films and analyzing them without their consent will fail. At the same time, applying the algorithms that I will give below for this list is quite simple. I would also like to note that during my work with one of the domestic film companies for their needs in the Wolfram Language language a parser was written that uploaded information about films from the KinoPoisk website (the legal side of the issue was settled) for the subsequent automatic generation of an advertising booklet about several thousands of films the rights to which belonged to this company. Below you can see an example of one such fully automatically created page of a booklet (the non-final version is given, due to the NDA).


This article will use the information on films presented on Wikipedia, which will avoid any problems with copyright holders. On the one hand, this complicates the task (a parser from a centralized repository like IMDB or KinoPoisk is easier to write), but at the same time it allows you to build some additional, interesting programs.

Import data from Wikipedia site

To get started, we’ll upload a symbolic representation of the HTML code of the Wikipedia page “ 250 best films according to IMDb ” (in the document, we will display only part of the result using the Short function ):

In [2]: =



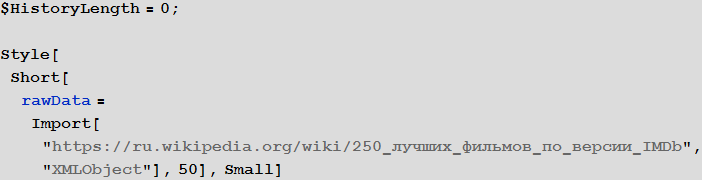
Out [3] =



Now select the links to the films, shown on the page in the table:

In [4]: ​​=



Out [4] =



Create a function that loads and saves a symbolic representation of the HTML code of the pages of each movie:

In [5]: =

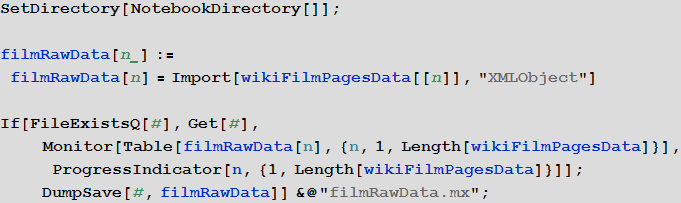
Secondary functions

Let's create a set of helper functions that we need to process the immersed symbolic HTML:

• A function to remove HTML wrappers, leaving only data:

In [8]: =

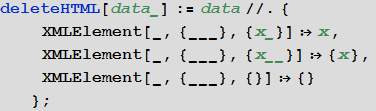
• A function that determines whether some string can be a word in Russian (i.e., consists of the letters of the Russian alphabet or hyphen):

In [9]: =



In [10]: =

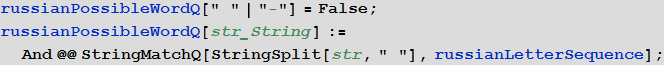
• A function that determines whether a certain string can be a word in Russian or English (i.e., consists of the letters of the Russian, English alphabet or hyphen):

In [12]: =



In [13]: =

• A function that converts (in a string) uppercase letters of the Russian alphabet to uppercase:

In [15]: =



In [16]: =

• To analyze the descriptions of films, we need information on the words of the Russian languages ​​and the relationships between the forms of the same word. We will load the morphological dictionary of the Russian language, created by academician Andrei Anatolyevich Zaliznyak :

In [17]: =



Out [17] =

• We process the dictionary data, compiling on its basis a list of Russian language words ( russianWords ) and a list of rules for replacing Russian word forms in their standard form ( russianWordsStandardForm ):

In [18]: =



The dictionary contains 2 645 347 words:

In [19]: =



Out [19] =



Out [20] =

• Create a function that checks whether a word is contained in the dictionary, as well as a function that converts the Russian word into its standard form:

In [21]: =



In [22]: =



Examples of how the functions work:

In [23]: =



Out [23] =



In [24]: =



Out [24] =

• Create a function that will determine if the word is an adjective:

In [25]: =



In [26]: =

Data processing

Now you can process the data of each of the films. At the same time, at the output, the filmsData variable , based on the Association function , will be stored in the filmsData variable , which will allow us to access data very easily.

In [27]: =



In [29]: =



An example of accessing the generated database by the film number:

In [31]: =



Out [31] =



An example of an appeal with a request about the director and year of release of each of the films:

In [32]: =



Out [32] // Short =

Some statistics based on data

To begin with, just create a collage of posters of all films:

In [33]: =



Out [33] =



Let's build the distribution of the number of films depending on the year:

In [34]: =



Out [34] =



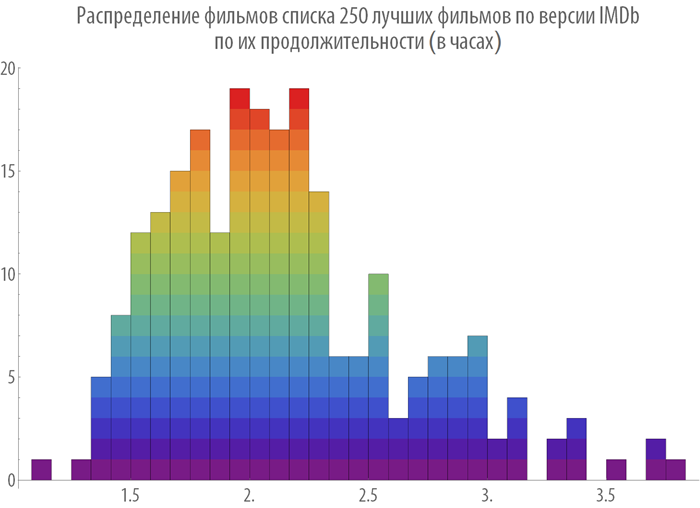
Let's build the distribution of films by their duration:

In [35]: =



Out [35] =



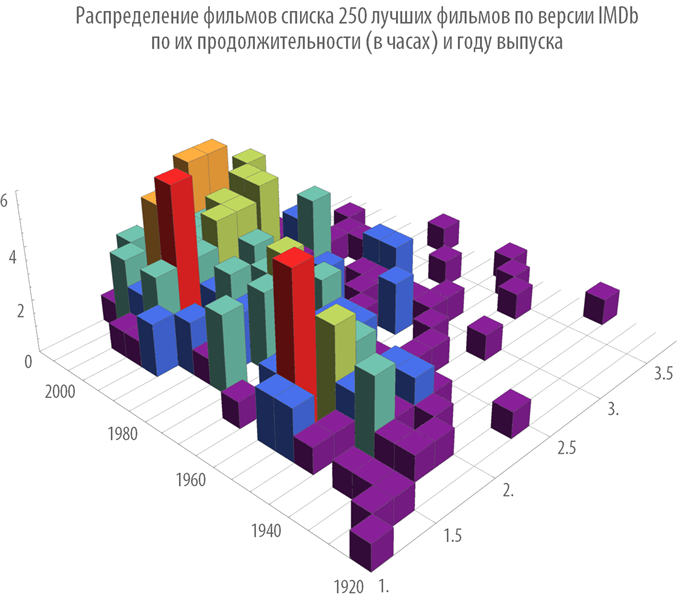
Let us construct the distribution of films by their duration and year of release:

In [36]: =



Out [36] =



The first 10 actors by the number of films in which they played:

In [37]: =



Out [37] =



The first 10 directors by the number of films they made:

In [38]: =



Out [38] =



The first 10 directors by the number of films the script for which they wrote:

In [39]: =



Out [39] =



The first 10 countries by the number of films to which they wrote music:

In [40]: =



Out [40] =



The first 10 countries by the number of films that were shot in them:

In [41]: =



Out [41] =



The first 10 genres by the number of films that belong to them:

In [42]: =



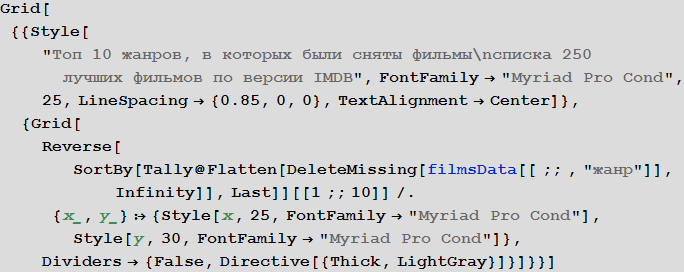
Out [42] =



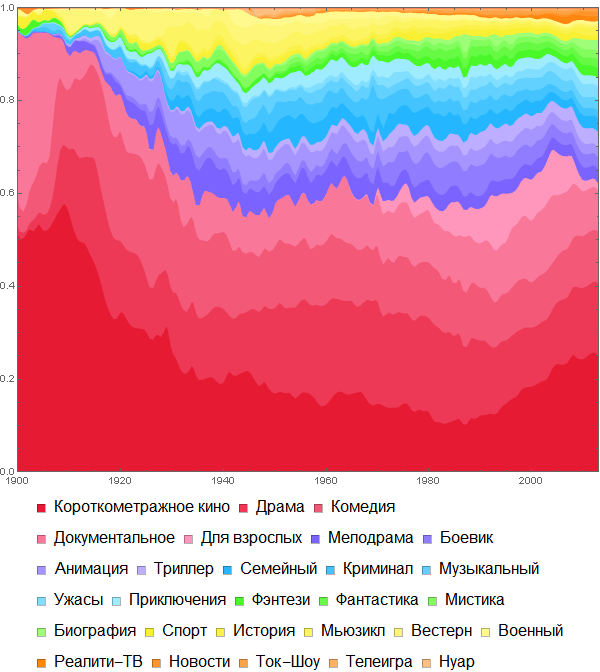
For those who are interested in movie genres, I can recommend the article “ Movies and Mathematica: Importing and Processing Information from the IMDB Database ” written a while ago , in which, in particular, the following distribution of films by genre was obtained:

The function that determines the distance between the films

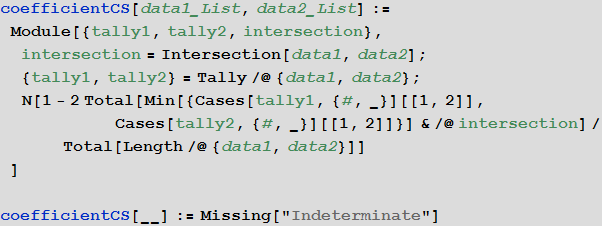
To determine the measure of difference between two lists of objects, we will use a generalization of the Chekanovsky-Sørensen coefficient (measure) :

In [43]: =



Example:

In [45]: =



Out [45] =



To determine the proximity of descriptions using this coefficient, we create a function that selects from the description of the film, the words of the Russian language with their translation into the standard form:

In [46]: =



Example of the function (in addition, the frequency of each word was calculated using the Tally function , while the frequencies were sorted by decreasing them):

In [47]: =



Out [47] =



Now let's create a function that determines the degree of closeness of films to each other. It represents the sum of several parameters normalized to unity with different weights. A total of 11 similarity parameters were taken: film description, genre (s), director, screenwriter (s), actors, cameraman (s), composer (s), country of production (s), year of release, duration, proximity of posters. In this case, you can set them different weights, but by default they will be the same.

In [48]: =



For future work, we select films for which at least some information is known (due to the fact that for several films their Wikipedia pages are empty):

In [62]: =



We calculate all measures of proximity (distance) between films :

In [63]: =

Analysis of the relationship between films

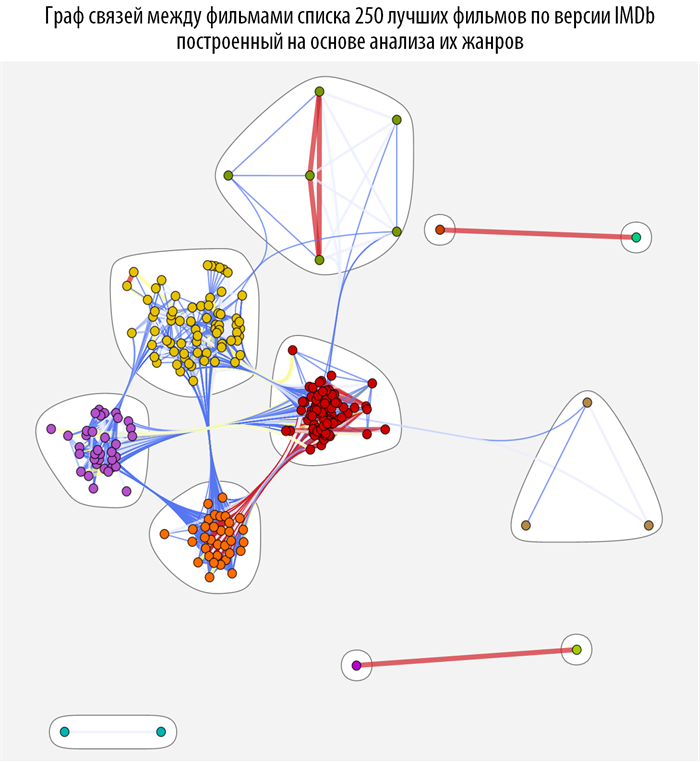
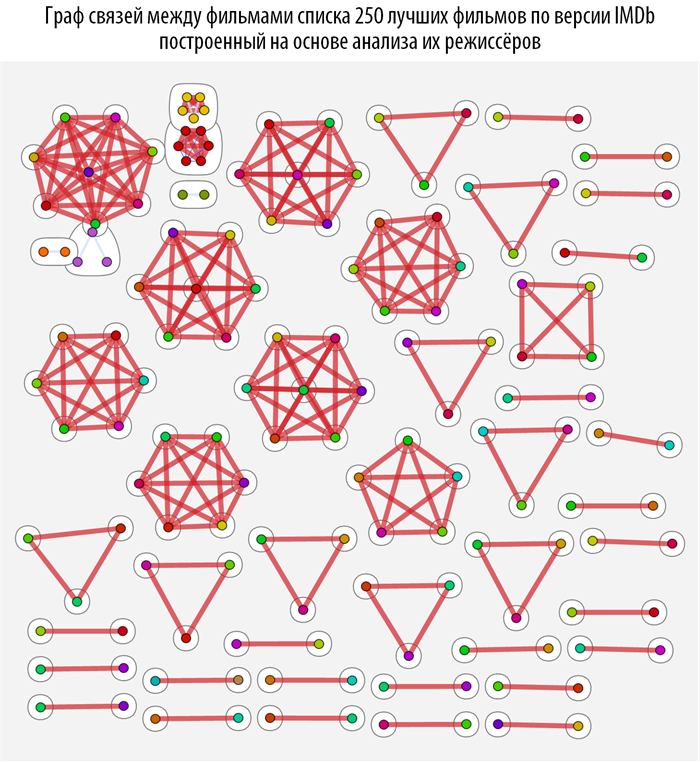
We study the connections between films using graph theory methods, namely, using the theory of the structure of the community in graphs . To do this, create a function based on CommunityGraphPlot :

In [64]: =



This function searches, based on the earlier built-in function of the distance between the films, the community in the graph, the more red and thicker the connection between the vertices, the closer they are (closer). When you hover over each of the vertices of the graph, you can get a tooltip with a poster and a movie name (you can download the document with interactive graphs and source code from the link provided at the very beginning of the post).



In [65]: =



Out [65] =



In [66]: =



Out [66] =



In [67]: =



Out [67] =



In [68]: =



Out [68] =



In [69]: =



Out [69] =



In [70]: =



Out [70] =



In [71]: =



Out [71] =



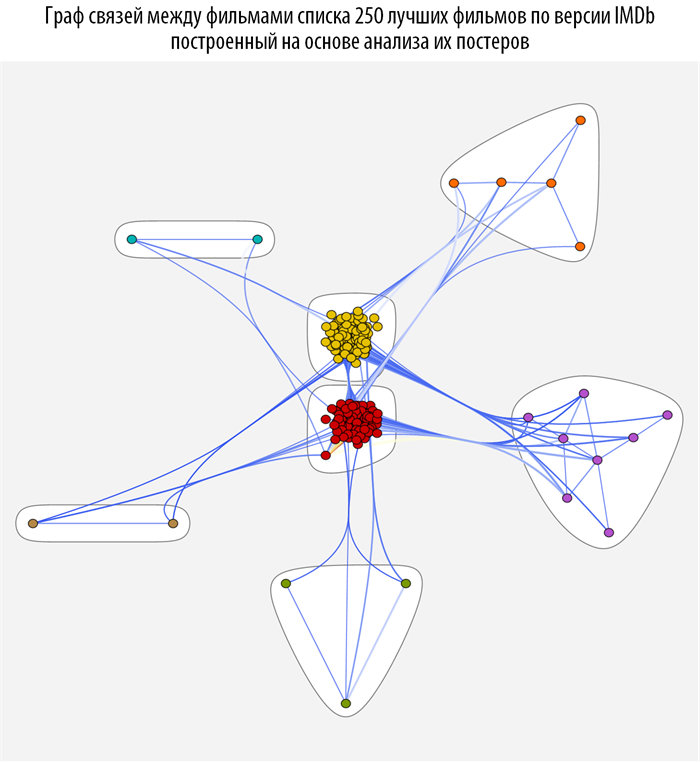
In [72]: =



Out [72] =

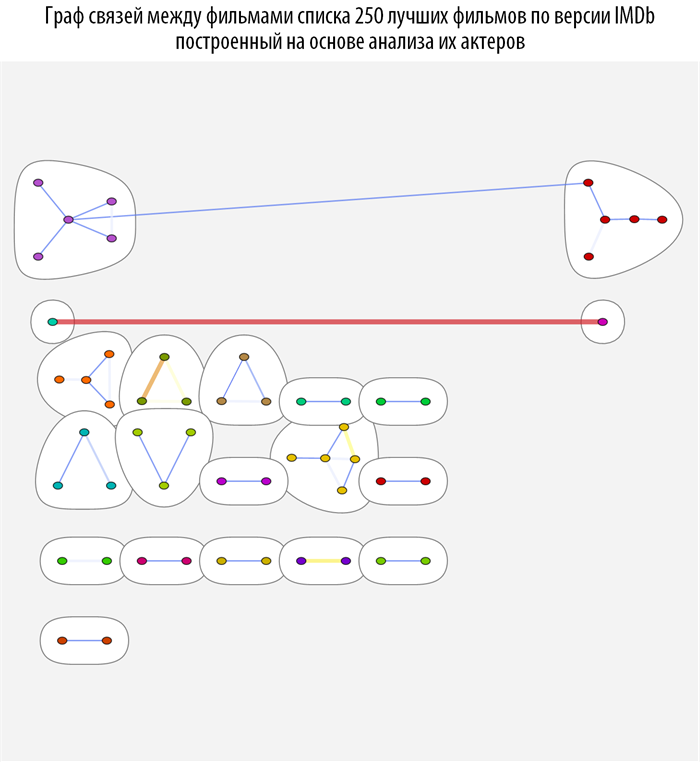
Building the optimal sequence for watching movies

We have done quite a lot of work and now, finally, we can build the optimal sequence for watching movies:

In [73]: =



So, now we can get it (the function provides output either in the form of a table or as a poster from posters):

In [74 ]: =




You can also display it in the form of a poster from the posters (the sequence of watching films will be from left to right, from top to bottom):

In [75]: =



Out [75] =



We can also consider the optimal sequences according to individual criteria:

Conclusion

I hope that my post was able to interest you, and some of the ideas and programs presented in it will be useful to you. Of course, you can think of many ways to use these algorithms, their further expansion and improvement. Many things have been specially simplified by me, since not all ready-made codes can be fully laid out in the public domain. I think that if you are interested, you can create a parser yourself from KinoPoisk or IMDB directly (in the latter case, the article can help youabout loading and analyzing information from IMDB databases, laid out by these resources in the public domain) and based on it already make even more detailed and high-quality analysis of the movie, as well as improve the optimal sequence of watching movies obtained in this article. I hope that all of these tasks will interest you too!

Resources for learning Wolfram Language ( Mathematica ) in Russian: http://habrahabr.ru/post/244451