Comparison of linear model building speed in R and Eviews
If you need to evaluate an econometric model with a small number of observations, then the software in which this can be done is determined solely by your preferences and financial capabilities. But if the number of observations is large? Regression is not always evaluated in an instant. In this post, I compare the linear regression estimation time in R and Eviews depending on the number of observations.
For this test we will use a simple linear regression:
y i = 10 + 5x i + ε i
We will change the number of observations N in the regression and compare the estimation time for each. I took N from 100,000 to 10,000,000 in increments of 100,000.
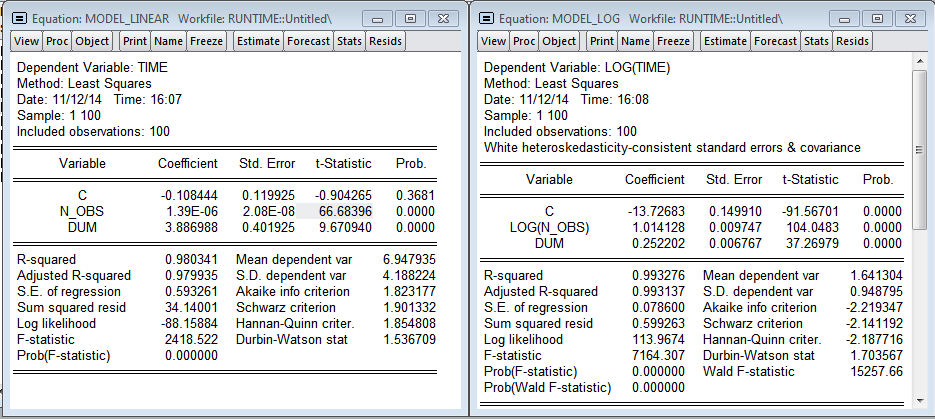
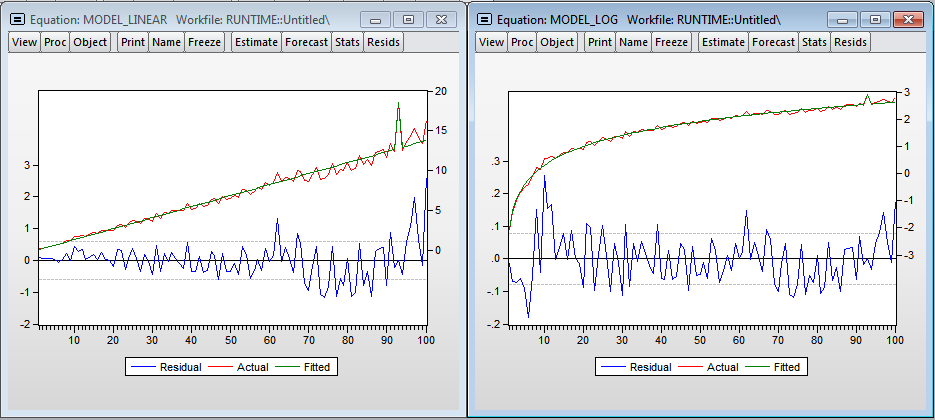
I added the dum variable - dummy for one of the observations (you can see the outlier on the chart, at that moment I needed to open the browser). As expected, the number of observations significantly affects the construction time of the regression. The multiplicative model gives more beautiful results. There is even a hint of the normality of the residuals in the regression. According to the linear model, we get that each additional million observations increases the construction time by 1.39 seconds, and the model in the logarithms shows the elasticity of the number of observations over time 1.014 (i.e. if the number of observations increases by 1%, then the regression calculation time will increase by 1.014%) .
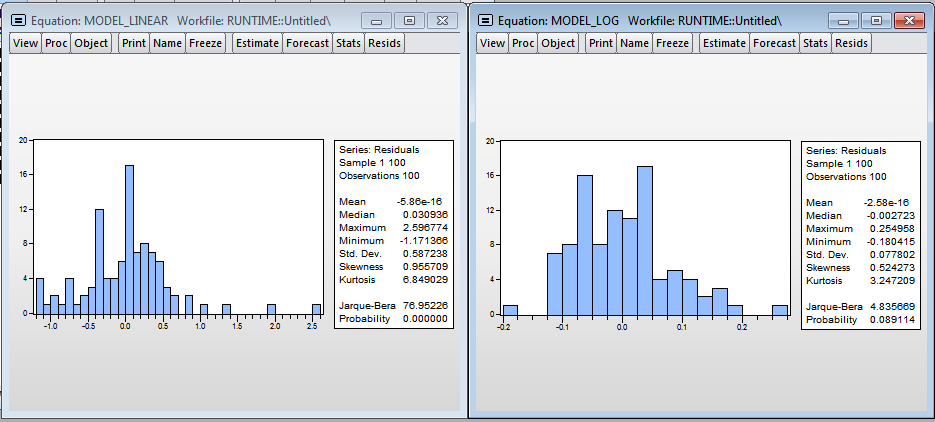
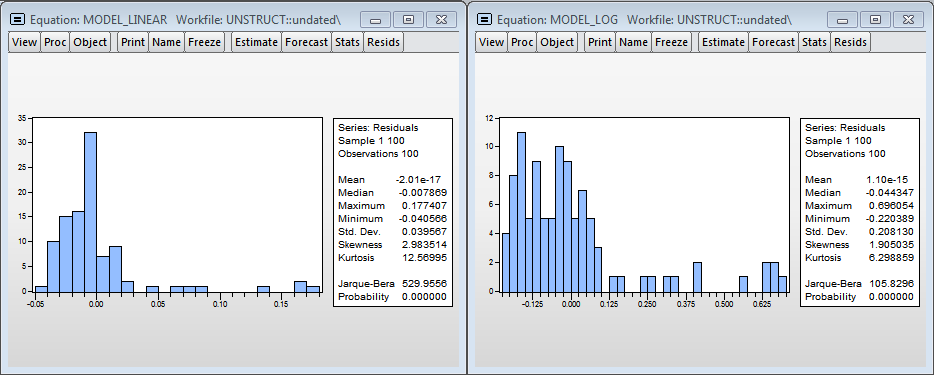
Visually, histograms of the remainder of the models are not similar to the normal distribution, which means that the estimates obtained in the models are biased, because, most likely, we do not take into account a significant variable - the processor load level. Nevertheless, the hypothesis of normality can be accepted in the logarithmic model (since the critical value of the Harkey-Behr test statistics is 8.9% and exceeds the standard critical significance level of 5%).
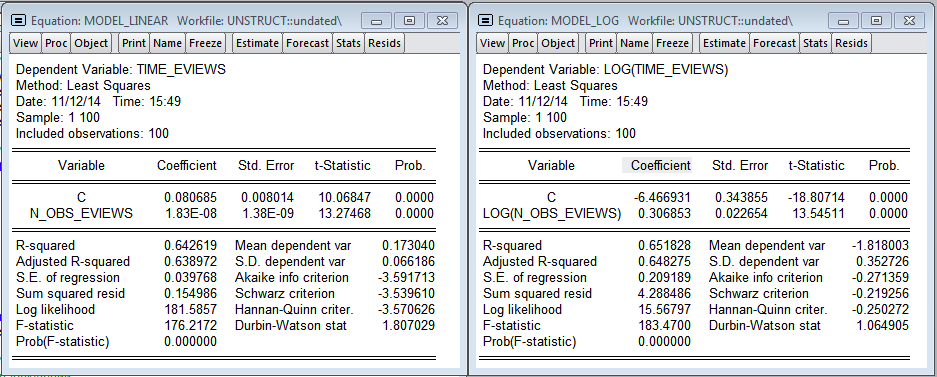
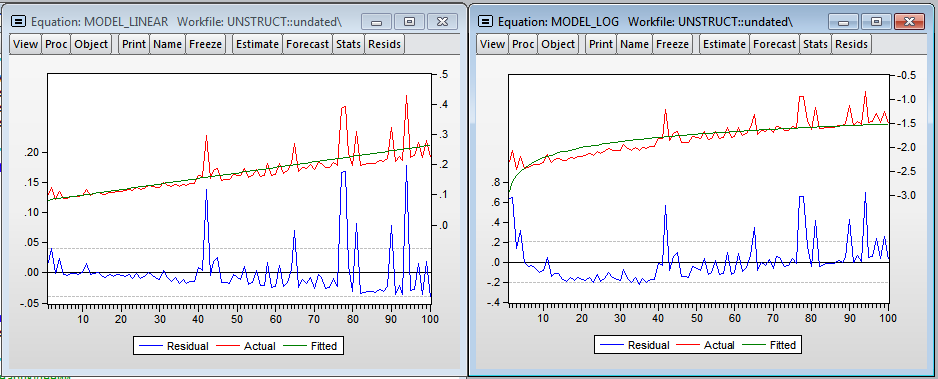
The models obtained at Eviews do not describe the dependence of the construction time on the number of observations in such a high quality. The linear model predicts that an additional million observations will increase the model evaluation time by 0.018 seconds (75.8 times less than in R). In the logarithmic model, the elasticity is 0.306 (3.3 times less than in R).
The graphs show a significant amount of outliers, which most likely indicates a much more significant effect of processor load on the calculation time in Eviews. There is heteroskedasticity in errors, which testifies to the inclusion of a variable - the processor load level in the model. It should be noted that Eviews practically does not consume RAM, while R cumulatively increases the amount of memory consumed for its needs and does not free it until the program is closed.
Again, the residuals in the models are not normal, you need to add more variables.
In the end, I want to say that you should not immediately write this in R as a minus. Perhaps this different calculation time happened because the lm () function that I used in R creates a large object of type lm which contains a lot of information about the estimated model and for 100,000 observations already weighs about 23 Mb, which, again, is stored in random access memory. If you are interested, you can repeat a similar test using any other functions from R or, for example, implement the gradient descent algorithm, which can be found here .
For this test we will use a simple linear regression:
y i = 10 + 5x i + ε i
We will change the number of observations N in the regression and compare the estimation time for each. I took N from 100,000 to 10,000,000 in increments of 100,000.
What came of it
Results R (Linear and Logarithmic Models)
I added the dum variable - dummy for one of the observations (you can see the outlier on the chart, at that moment I needed to open the browser). As expected, the number of observations significantly affects the construction time of the regression. The multiplicative model gives more beautiful results. There is even a hint of the normality of the residuals in the regression. According to the linear model, we get that each additional million observations increases the construction time by 1.39 seconds, and the model in the logarithms shows the elasticity of the number of observations over time 1.014 (i.e. if the number of observations increases by 1%, then the regression calculation time will increase by 1.014%) .
Bar Charts
Visually, histograms of the remainder of the models are not similar to the normal distribution, which means that the estimates obtained in the models are biased, because, most likely, we do not take into account a significant variable - the processor load level. Nevertheless, the hypothesis of normality can be accepted in the logarithmic model (since the critical value of the Harkey-Behr test statistics is 8.9% and exceeds the standard critical significance level of 5%).
Eviews Results (Linear and Logarithmic Models)
The models obtained at Eviews do not describe the dependence of the construction time on the number of observations in such a high quality. The linear model predicts that an additional million observations will increase the model evaluation time by 0.018 seconds (75.8 times less than in R). In the logarithmic model, the elasticity is 0.306 (3.3 times less than in R).
The graphs show a significant amount of outliers, which most likely indicates a much more significant effect of processor load on the calculation time in Eviews. There is heteroskedasticity in errors, which testifies to the inclusion of a variable - the processor load level in the model. It should be noted that Eviews practically does not consume RAM, while R cumulatively increases the amount of memory consumed for its needs and does not free it until the program is closed.
Again, the residuals in the models are not normal, you need to add more variables.
In the end, I want to say that you should not immediately write this in R as a minus. Perhaps this different calculation time happened because the lm () function that I used in R creates a large object of type lm which contains a lot of information about the estimated model and for 100,000 observations already weighs about 23 Mb, which, again, is stored in random access memory. If you are interested, you can repeat a similar test using any other functions from R or, for example, implement the gradient descent algorithm, which can be found here .
Code in R
library(ggplot2)
#Создаем векторы, которые будут содержать кол-во наблюдений и время выполнения
N <- seq(100000,10000000, by = 100000)
time.vector <- rep(0,length(N))
#Строим линейную регрессию для каждого кол-ва наблюдений из вектора N и запоминаем время построения
count = 1
for (n in N) {
X <- matrix(c(rep(1,n),seq(1:n)),ncol = 2)
y <- matrix(X[, 1] * 10 + 5 * X[, 2] + rnorm(n,0,1))
t <- Sys.time()
lm1 <- lm(y ~ 0 + X)
t1 <- Sys.time()
lm1.time <- t1 - t
time.vector[count] <- lm1.time
count <- count + 1
}
#Рисуем картинку и записываем данные в файл
times <- data.frame(N,time.vector)
names(times) <- c('N_obs','Time')
ggplot(data = times, aes(N_obs, Time, size = 2)) + geom_point()
write.csv(times,'times.csv')
Code in Eviews
'Создаем workfile, вектор кол-ва наблюдений и времени исполнения
wfcreate(wf=unstruct, page=undated) u 10000000
scalar time_elapsed = 0
series time_eviews = 0
series n_obs_eviews = 0
'Строим линейную модель, такую же как в R, по таким же кол-вам наблюдений, запоминаем время построения
for !n = 1 to 100
smpl @first @first + !n * 100000 - 1
series trend = @trend+1
series y = 10 + 5 * trend + nrnd
tic
equation eq1.ls y c trend
time_elapsed = @toc
smpl @first + !n - 1 @first + !n - 1
time_eviews = time_elapsed
n_obs_eviews = !n * 100000
next
smpl @first @first + 99
'Оцениваем линейную и логарифмическую модели времени от кол-ва наблюдений
equation model_linear.ls time_eviews c n_obs_eviews
show model_linear
equation model_log.ls log(time_eviews) c log(n_obs_eviews)
show model_log
