Birch-Swinnerton-Dyer Conjecture
This remarkable hypothesis connects the behavior of the function L where it is currently unknown whether it is defined and the order of the group III , about which it is not known whether it is finite!
JTTate, The arithmetic of elliptic curves, Inventiones mathematicae 23 (1974)
Original
(A brief reference about the relevance of the quote 40 years ago: after Wiles and Co., it became known that the function L can be defined on the entire complex plane. The finiteness of the group III in the general case remains unknown.)This remarkable conjecture relates the behavior of a function L at a point where it is not at present known to be defined to the order of a group W which is not known to be finite!
It remains to discuss the possibility of error. As a precaution against internal computer errors, you can run all the calculations twice or do checks inside the program. Moreover, computers — unlike humans — are designed so that their errors are usually too large to be overlooked. We are sure that there are no such errors in our results. On the other hand, when coding an intricate scheme of computation into a computer program, programming errors are inevitable. Most of them are detected even before the main launches, due to the fact that the program hangs or produces ridiculous results. But the program, which is considered to be working, can still contain logical errors that occur under rare circumstances: indeed, most computers are subject to anomalies, due to which they sometimes behave differently, as they should according to the specifications. In essence, our program for step (ii) turned out to be inaccurate and missed a very small number of equivalences that should have been found.
For these reasons, we believe that you should not automatically trust the results obtained on a computer. In some cases, they can be checked at the expense of properties that were not essentially involved in the calculations and which would hardly survive a possible error. (For example, a table of values of a smooth function obtained without interpolation can be checked by calculating the differences of neighboring values.) But if such checks are not available, you should not completely trust the results until they were independently confirmed by another programmer on another computer. We do not think that this sets an excessive standard at a time when computers are becoming so widely available; and we are sure that low standards have already led to publication and belief in incorrect results.
BJBirch and HPFSwinnerton-Dyer, Notes on elliptic curves. I, Journal für die reine und angewandte Mathematik 212 (1963)
Original
It remains to discuss the question of error. One can take precautions against machine errors either by running all the calculations twice or by checks included in the program. Moreover, machines - unlike human beings - are so designed that the errors they make are usually too gross to be overlooked. We are satisfied that there are in our results no undetected errors of this sort. On the other hand, in translating an elaborate scheme of calculation into a machine program one is bound to make mistakes. Most of these are found before the program is used for production runs; they show up because the program grinds to a halt or produces ridiculous results. But a program which is believed to work may still contain logical errors which only have an effect in rare circumstances: and indeed most computers have anomalies which cause them occasionally not to behave in the way that their specifications suggest. In fact, our program for stage (ii) was imperfect in that a very few equivalences were missed by the machine.
For these reasons we believe that results obtained from a computer should not be automatically trusted. In some cases they can be checked because they have properties which were not essentially used in the course of the calculation and which would be unlikely to survive if an error had been made. (For example, if a table of a smooth function has been calculated without the use of interpolation, it can be checked by differencing.) But if checks of this sort are not available, results should not be fully trusted until they have been independently reproduced. by a different programmer using a different machine. We do not think this sets an unreasonable standard, now that computers are becoming so widely available; and we are satisfied that lower standards have already led to a number of untrue results being published and believed.
For these reasons we believe that results obtained from a computer should not be automatically trusted. In some cases they can be checked because they have properties which were not essentially used in the course of the calculation and which would be unlikely to survive if an error had been made. (For example, if a table of a smooth function has been calculated without the use of interpolation, it can be checked by differencing.) But if checks of this sort are not available, results should not be fully trusted until they have been independently reproduced. by a different programmer using a different machine. We do not think this sets an unreasonable standard, now that computers are becoming so widely available; and we are satisfied that lower standards have already led to a number of untrue results being published and believed.

There will be no hypothesis formulation under the cut; knowledgeable expressions like “Euler product” and “holomorphic continuation” (both in terms of language and in terms of designated concepts) can read a five-page pdf from the Clay Institute website. Under the cut is some attempt to clarify in which direction the development of mathematical thought in general is the Birch-Swinnerton-Dyer hypothesis. And also - how to count to large numbers like those shown on the KDPV in less than a second.
It will be about finding rational solutions to equations with two variables.
Linear and quadratic equations
The simplest case is linear equations: a x + b y + c = 0 (where a , b , c are rational). Here the solution is simple: if we exclude degenerate cases with a = b = 0, one of the variables can take any rational value, and the other is uniquely calculated from the first.
The next case is quadratic equations. Here different cases longer, but if you delete the ones where everything is clear ( y - x ² = 0, y ²- x ² = 0), the remaining linear change of variables reduces to a x ² +b y ² + c = 0, where a , b , c are nonzero rational. Let's take three characteristic examples:

Obviously, the first example has no rational solutions, because the left side is always not less than one and cannot be equal to zero. We can put it another way: the first example does not even have real solutions, and rational numbers are a subset of real ones, so there are no rational solutions either.
It is less obvious that the second example has no rational solutions. Reduce x and y to the least common denominator, let x = k / n , y = m / n , where k , m , ninteger and mutually simple in the aggregate (that is, there is no number greater than one that simultaneously divides all three). Then the equation is converted to form
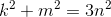 .
. Consider it modulo 3. The square of an integer modulo 3 can be either 0 or 1; the sum of two squares modulo 3 can be zero only if both numbers are divisible by 3. Therefore, k and m must be divisible by 3.
Now we take modulus 9 = 3². The left side is divisible by 9, hence 3 n ² should be divisible by 9 and n should be divisible by 3. Therefore, there are solutions where k , m , ninteger and mutually simple in the aggregate, does not exist, and the original equation does not have rational solutions, as promised.

The third equation has several solutions to indicate easily: for example, x = 1, y = 0. When one solution of the quadratic equation is known, it is not difficult to find everything by a method dating back to Diophantus: a line passing through the point (1,0) intersects the circle at exactly one point, and this point will be rational if and only if the corner direct coefficient is rational. Specifically for a circle, if we denote the angular coefficient by - t , the straight line has the form y = (1- x ) t , and the second intersection point with the circle x ² +y ² = 1 has coordinates
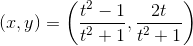 - this is the general solution of the third example (with the exception of the point (1,0) itself, which in a sense corresponds
- this is the general solution of the third example (with the exception of the point (1,0) itself, which in a sense corresponds  ).
).Hasse principle
The idea to give equations with integer or rational coefficients modulo some prime number, as well as powers of the same number, is extremely fruitful. The special construction “let's say that we are only interested in what happens modulo p , p ² and all other degrees p immediately, and we ignore other arithmetic properties” is called “ p-adic numbers"(there could be a link to Wikipedia, but scary words sometimes come across there); p-adic numbers, like real ones, contain rational numbers and add many others (for example, the square root of 2 is extracted modulo 7 and all degrees sevens, so that it is among the 7-adic numbers; on the other hand, it is not extracted either modulo 4 or modulo 3, so that it is not among the 2- and 3-adic numbers). carry over to 3-adic numbers, and we can say: the second example does not even have 3-adic their solutions, and rational numbers are a subset of 3-adic ones, so there are no rational solutions either.
Working with one prime number is often easy and enjoyable. In the end, all the modulo prime numbers can be sorted out. On the other hand, working with more than one prime number tends to be much more difficult - Goldbach problem and the problem of simple twins to vivid evidence.
 Passing to real and p-adic numbers helps to prove well that there are no solutions. And vice versa, the Hasse principle says that if there are real and p-adic solutions for all p, then there are necessarily rational solutions. (Of course, there are infinitely many primes, and the test of all can be delayed. But we can prove that if p does not divide either the numerators or the denominators a , b ,c and greater than 2, then there are always p-adic solutions, and for the divisors abc one can effectively verify the existence of solutions using the law of quadratic reciprocity.)
Passing to real and p-adic numbers helps to prove well that there are no solutions. And vice versa, the Hasse principle says that if there are real and p-adic solutions for all p, then there are necessarily rational solutions. (Of course, there are infinitely many primes, and the test of all can be delayed. But we can prove that if p does not divide either the numerators or the denominators a , b ,c and greater than 2, then there are always p-adic solutions, and for the divisors abc one can effectively verify the existence of solutions using the law of quadratic reciprocity.) Unfortunately, the Hasse principle is not satisfied for equations of a higher degree. For example, one can prove that the equation 3 x 3 +4 y 3 + 5 = 0 has real and p-adic solutions for all p, but does not have rational solutions.
Elliptical curves
An equation of the third degree, if, again, we cross out different degenerate cases like y ( x ²-1) = x 3 -1 and y ² = x 3 + x ², defines a curve of genus 1 (this is not a definition, there are other curves of genus 1). There may not be points on the curve (solutions to the equation). If there are points, and if one of them is selected, an elliptic curve is obtained ; in the case of an elliptic curve, you can always change the variables to send the selected point to infinity and get an equation of the standard form y ² = x 3 + a x + b , a ,b rational (and even integers, you can always get rid of the denominators by another change of variables), which we will do: only elliptic curves (above rational numbers) will come next.
Informally speaking, exactly how the Hasse principle is violated for a single elliptic curve and related entities, it is characterized by the Tate - Shafarevich group of the curve, with Tate's presentation traditionally denoted by Cyrillic III even in articles where most letters are English. It is assumed that it is finite. The Birch-Swinnerton-Dyer hypothesis involves the order of this group.
 Unlike quadratic equations, after finding one point (and sending it to infinity), everything just starts. It is well known thatpoints on an elliptic curve can be added. If you take one point and begin to add it to itself ( P , P + P = 2 P , P + P + P = 3 P , ...), then two options are possible: either after a certain number of steps you get an infinitely remote point (after which the next step will give P again and the process will loop), or all the resulting points will be different (and then it makes sense to take also - P , - 2P, and so on). In the first case, the point is called the torsion point.; for a single curve, there can be from 1 to 12, excluding 11 (the always existing infinitely distant point is also a torsion point). The Mordell – Weil theorem states that one can always find a finite number (possibly 0) of points of the second type P 1 , ..., P r such that any point on the curve is uniquely written in the form n 1 P 1 + ... + n r P r + Q , where Q is some torsion point, and n i are integers. The number r is called the rank of the curve. For example, the curve y ² = x3 + 877 x , drawn on KDPV, has a rank of 1 and two torsion points; any (rational) point of the curve is either n P or n P + (0,0), where the P coordinates are signed in the picture.
Unlike quadratic equations, after finding one point (and sending it to infinity), everything just starts. It is well known thatpoints on an elliptic curve can be added. If you take one point and begin to add it to itself ( P , P + P = 2 P , P + P + P = 3 P , ...), then two options are possible: either after a certain number of steps you get an infinitely remote point (after which the next step will give P again and the process will loop), or all the resulting points will be different (and then it makes sense to take also - P , - 2P, and so on). In the first case, the point is called the torsion point.; for a single curve, there can be from 1 to 12, excluding 11 (the always existing infinitely distant point is also a torsion point). The Mordell – Weil theorem states that one can always find a finite number (possibly 0) of points of the second type P 1 , ..., P r such that any point on the curve is uniquely written in the form n 1 P 1 + ... + n r P r + Q , where Q is some torsion point, and n i are integers. The number r is called the rank of the curve. For example, the curve y ² = x3 + 877 x , drawn on KDPV, has a rank of 1 and two torsion points; any (rational) point of the curve is either n P or n P + (0,0), where the P coordinates are signed in the picture. All torsion points are relatively easy to find. For example, in the case of integer coefficients a and b, all torsion points (except for the infinitely distant one) themselves have integer coordinates, and the y- coordinate is either zero or y ² divides 4 a 3 +27 b ². The calculation of rank and the search for generating points P i are much more complicated.
It's time to figure something out
You can search for points on the curve by simply sorting the numerator and denominator of the x- coordinate in ascending order and checking if a rational y is obtained . It is easy to see that in the case of integer coefficients of the curve, the denominator x should be an exact square, and the denominator y should be a cube of the same number (the denominators on the KDPV are 78841535860683900210 squared and cube), which makes life a little easier. However, the KDPV curve is specially chosen so that a look at it suppresses such thoughts in the bud ( P is the point with the lowest denominator, not counting (0,0)).
In principle, there is a general procedure for n- descent ( nIs a natural number not less than 2), which allows us to calculate r and find r independent points if the Tate-Shafarevich group has no elements of order n , and obtain an upper and lower bound on r and find some independent points in the general case. (In the latter case, the descent can be repeated, choosing as n the increasing degrees of some prime number; if the Tate-Shafarevich group is finite, then after a finite time the process will converge.) But in practice, it is extremely inconvenient. Birch and Swinnerton-Dyer in the first of two articles proposed a method for 2-descent, not going beyond the scope of real arithmetic. Those who want an accurate description can look at the source code mwrank, and specifically in mwrank1.cc , here are some results for y ² = x 3 +877 x .
At the first stage, the method searches for quartics - curves of the form
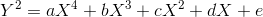 - from which there is a mapping to the original curve by sorting a , b , c in certain ranges, calculating d and e , checking that d and e are obtained integer, and dropping those quartics onto which there are no real points or p-adic points for at least some p .
- from which there is a mapping to the original curve by sorting a , b , c in certain ranges, calculating d and e , checking that d and e are obtained integer, and dropping those quartics onto which there are no real points or p-adic points for at least some p .After the first stage, some quartics may turn out to be equivalent (pass into each other by a linear fractional change of X ). At the second stage, the method leaves one quartic from each equivalence class. After this, there remains 2 m + k -1 quartics, where the factor 2 k is 1.2 or 4 if there are 0.1.3 points of order 2 (which are characterized by y = 0) on the original curve , and m is the upper bound for rank. On the curve y ² = x 3 + 877 x there is one point of order 2, and the rank is unity, so that three quartics are obtained.
First one:
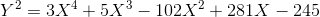
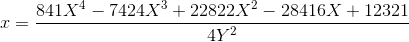
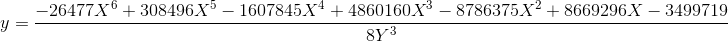
(The Habr format does not favor writing out formulas for all coefficients, but nevertheless they are: all the coefficients in the coordinate transformation are calculated through a , b , c , d , e , for example, 12321 is obtained as d ²-8 e c / 3. )
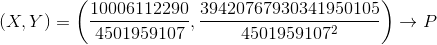
Second:
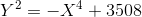
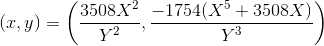

Third:
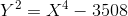
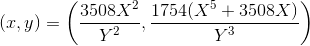
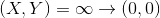
(On a quartic there can be 0 or 2 infinitely distant points, depending on whether a is an exact square; on the first two quartics there were none, there are two of them, both go to (0,0). Replacement
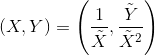 reduces them to ordinary points.)
reduces them to ordinary points.)At the third stage, the method searches for a rational point on the quartics remaining after the second stage. The numerator and denominator of the x- coordinate on the original curve are approximately equal in order to the fourth degree of the numerator and the denominator of the X- coordinate in the quartic (multiplying by n on an elliptic curve is an operation of degree n², for a 2-descent, a degree of 4) is obtained. If the point was found, then using it you can calculate the point on the original curve. If the point could not be found, then a problem arises: this can mean either that it really does not exist (and there are non-trivial elements of the Tate-Shafarevich group), or that they were poorly searched. The theoretical solution is to simultaneously launch a higher order descent and search for points with large numerators and denominators. A good practical solution is unknown.
For the case of the curve y ² = x 3 + 877 x, the coordinates on the quartics look less impressive than the coordinates of the points of the original curve, but are still too large for direct enumeration. However, with a quartic
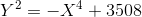 can go down further. (It is difficult to work with the first quartic further, but it is not necessary: one generating point is quite enough.) The right-hand side is biquadratic, that is, it is expressed in terms of X ²; this always happens when there is a second-order point on the initial curve (with y = 0). If we take the pair ( X ², Y ) as variables , we get a quadratic equation, which can already be solved:
can go down further. (It is difficult to work with the first quartic further, but it is not necessary: one generating point is quite enough.) The right-hand side is biquadratic, that is, it is expressed in terms of X ²; this always happens when there is a second-order point on the initial curve (with y = 0). If we take the pair ( X ², Y ) as variables , we get a quadratic equation, which can already be solved: 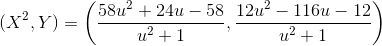
Next, any common divisor of the numerator and denominator of the expression for X ² must also divide
 ; their quotient can be squared only if they both have the form " d times the square", where d- the divisor 3508, free from squares, that is, one of the numbers 1,2,877,1754 (negative d are excluded, because the denominator is always positive). The numerator cannot be an exact square in 2-adic (and especially in rational) numbers. Trying d = 2:
; their quotient can be squared only if they both have the form " d times the square", where d- the divisor 3508, free from squares, that is, one of the numbers 1,2,877,1754 (negative d are excluded, because the denominator is always positive). The numerator cannot be an exact square in 2-adic (and especially in rational) numbers. Trying d = 2: 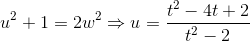 . Substituting the obtained expression for u into the numerator and requiring that the numerator be a double square, we obtain a new quartic
. Substituting the obtained expression for u into the numerator and requiring that the numerator be a double square, we obtain a new quartic  .
. She has a point, available to iterate:
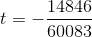 .
. The search for quartiles can be further reduced using the same idea of considering an equation modulo primes and powers of primes. When searching for integers k , m such that
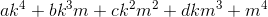 Is an exact square, for each prime p, approximately half of the p ² possible pairs of residues ( k , m ) give a non-square modulo p . (Instead of 2 and 3, it is better to look at their degrees 16 and 9; for large p, increasing the degree gives nothing.) Therefore, “good” pairs of residues modulo, for example, 16 * 9 * 5 * 7, about 1/16 of the total the number of possible pairs; it is enough to search only pairs ( k , m ) with “good” residues. The aforementioned mwrank, using similar considerations, finds a point P with an FDPC in less than a second.
Is an exact square, for each prime p, approximately half of the p ² possible pairs of residues ( k , m ) give a non-square modulo p . (Instead of 2 and 3, it is better to look at their degrees 16 and 9; for large p, increasing the degree gives nothing.) Therefore, “good” pairs of residues modulo, for example, 16 * 9 * 5 * 7, about 1/16 of the total the number of possible pairs; it is enough to search only pairs ( k , m ) with “good” residues. The aforementioned mwrank, using similar considerations, finds a point P with an FDPC in less than a second.Birch-Swinnerton-Dyer Conjecture

 In the first article, Notes on elliptic curves. I ”Birch and Swinnerton-Dyer collected statistics on the ranks of a couple of thousand elliptic curves. In the second article, “Notes on elliptic curves. II ”the time has come to analyze the accumulated statistics, the title hypothesis is also proposed there.
In the first article, Notes on elliptic curves. I ”Birch and Swinnerton-Dyer collected statistics on the ranks of a couple of thousand elliptic curves. In the second article, “Notes on elliptic curves. II ”the time has come to analyze the accumulated statistics, the title hypothesis is also proposed there. Working with an elliptic curve on rational numbers is sometimes problematic: the coordinates of points grow rapidly, the procedure for calculating the rank does not always give an answer. On the other hand, having an equation with integer coefficients, we can consider it modulo different prime numbers. The number of points modulo small primes is easy to calculate directly, but it is not clear what relation the numbers have to rational points.
If for each prime number we count the number of points on the curve modulo this prime number, we get some infinite set of integers. Hasse - Weil zeta function of an elliptic curve, traditionally denoted by the letter L, it turns out if, in a certain way, “glue” this set into one function of a complex variable. Since it contains information on the behavior modulo all primes at once, it can be difficult to prove something about it. (In this, it is similar to the Riemann zeta function - and the Riemann hypothesis regarding the properties of the Riemann zeta function is another of the “millennium problems.”) The Birch – Swinnerton-Dyer conjecture goes further and relates the behavior of the curve over rational numbers (specifically, rank) with the properties of the zeta function, calculated exclusively from the behavior of the curve with respect to finite modules.
