And again about GIL in Python
Foreword
The area in which I am fortunate to work is called computational electrophysiology of the heart . The physiology of cardiac activity is determined by electrical processes occurring at the level of individual myocardial cells. These electrical processes create an electric field that is easy to measure. Moreover, it is very well described in the framework of mathematical models of electrostatics. Here a unique opportunity arises to strictly mathematically describe the work of the heart, which means to improve methods of treatment for many heart diseases.
During my work in this area, I have gained some experience using various computing technologies. I will try to answer some questions that may be of interest not only to me as part of this publication.
Briefly about Scientific Python
Starting from the first courses of the university, I tried to find the ideal tool for the rapid development of numerical algorithms. If we discard a number of frankly marginal technologies, I ran between C ++ and MATLAB. This continued until I discovered Scientific Python [1].
Scientific Python is a collection of Python libraries for scientific computing and scientific visualization. In my work I use the following packages, which cover about 90% of my needs:
| Title | Description |
|---|---|
| Numpy | One of the basic libraries allows you to work with multidimensional arrays as single objects in the MATLAB style. It includes the implementation of the basic procedures of linear algebra, the Fourier transform, work with random numbers, etc. |
| Scipy | The NumPy extension includes the implementation of optimization methods, work with discharged matrices, statistics, etc. |
| Pandas | A separate package for the analysis of multidimensional data and statistics. |
| Sympy | Symbol Math Pack. |
| Matplotlib | Two-dimensional graphics. |
| Mayavi2 | Three-dimensional graphics based on VTK. |
| Spyder | Convenient IDE for interactive development of mathematical algorithms. |
Problems of parallel computing in Python.
By parallel computing in this article I will understand SMP - symmetric multiprocessing with shared memory. I will not deal with the use of CUDA and systems with separate memory (the MPI standard is most often used).
The problem is the GIL. GIL (Global Interpreter Lock) is a mutex that prevents multiple threads from executing the same bytecode. This lock, unfortunately, is necessary, since the memory management system in CPython is not thread safe. Yes, GIL is not a Python problem, but a CPython interpreter implementation problem. But, unfortunately, the rest of the Python implementations are not well suited for creating fast numerical algorithms.
Fortunately, there are currently several ways to solve GIL problems. Consider them.
Test task
Two sets of N vectors are given: P = {p 1 , p 2 , ..., p N } and Q = {q 1 , q 2 , ..., q N } in three-dimensional Euclidean space. It is necessary to construct a matrix R of dimension N x N , each element r i, j of which is calculated by the formula:

Roughly speaking, we need to calculate a matrix using pairwise distances between all vectors. This matrix is often used in real calculations, for example, during RBF interpolation or solving diffours in a state of emergency by the method of integral equations.
In test experiments, the number of vectors is N = 5000. For calculations, a processor with 4 cores was used. The results are obtained by the average time of 10 starts.
The full implementation of test tasks can be seen on GitHub [2].
Correct remark in comments from "@chersaya". This test case is used here as an example. If you really need to calculate pairwise distances, it is better to use the scipy.spatial.distance.cdist function.
C ++ parallel implementation
To compare the efficiency of parallel computing in Python, I implemented this task in C ++. The main function code is as follows.
Uniprocessor implementation:
//! Single thread matrix R calculation
void spGetR(vector & p, vector & q, MatrixMN & R)
{
for (int i = 0; i < p.size(); i++) {
Vector3D & a = p[i];
for (int j = 0; j < q.size(); j++) {
Vector3D & b = q[j];
Vector3D r = b - a;
R(i, j) = 1 / (1 + sqrt(r * r));
}
}
}
Multiprocessor implementation:
//! OpenMP matrix R calculations
void mpGetR(vector & p, vector & q, MatrixMN & R)
{
#pragma omp parallel for
for (int i = 0; i < p.size(); i++) {
Vector3D & a = p[i];
for (int j = 0; j < q.size(); j++) {
Vector3D & b = q[j];
Vector3D r = b - a;
R(i, j) = 1 / (1 + sqrt(r * r));
}
}
}
What is interesting here? Well, first of all, I used a separate Vector3D class to represent a vector in three-dimensional space. The overloaded operator "*" in this class has the meaning of a scalar product. To represent a set of vectors, I used std :: vector. For parallel computing, OpenMP technology was used. To parallelize the algorithm, it is enough to use the directive "#pragma omp parallel for".
Results:
| Uniprocessor C ++ | 224 ms |
| Multiprocessor C ++ | 65 ms |
Parallel Implementations in Python
1. Naive implementation in pure Python
In this test, I wanted to check how much the task will be solved in pure Python without using any special packages.
Solution Code:
def sppyGetR(p, q):
R = np.empty((p.shape[0], q.shape[1]))
nP = p.shape[0]
nQ = q.shape[1]
for i in xrange(nP):
for j in xrange(nQ):
rx = p[i, 0] - q[0, j]
ry = p[i, 1] - q[1, j]
rz = p[i, 2] - q[2, j]
R[i, j] = 1 / (1 + sqrt(rx * rx + ry * ry + rz * rz))
return R
Here p , q are the input data in the NumPy format of arrays of dimensions (N, 3) and (3, N) . And then comes an honest Python loop that calculates the elements of the matrix R.
Results:
| Uniprocessor Python | 57 386 ms |
2 Uniprocessor NumPy
In general, for computing in Python using NumPy, sometimes you don’t have to think about parallelism at all. So, for example, the procedure of multiplying two matrices by NumPy will eventually still be performed using low-level high-performance linear algebra libraries in C ++ (MKL or ATLAS). But, unfortunately, this is true only for the most common operations and does not work in the general case. Unfortunately, our test task will be performed sequentially.
The solution code is as follows:
def spnpGetR(p, q):
Rx = p[:, 0:1] - q[0:1]
Ry = p[:, 1:2] - q[1:2]
Rz = p[:, 2:3] - q[2:3]
R = 1 / (1 + np.sqrt(Rx * Rx + Ry * Ry + Rz * Rz))
return R
Only 4 lines and no cycles! That's why I love NumPy.
Results:
| Uniprocessor NumPy | 973 ms |
3 Multiprocessor NumPy
As a solution to GIL problems, it is traditionally proposed to use several independent execution processes instead of several execution threads. Everything would be fine, but there is a problem. Each process has independent memory, and we need to transfer a matrix of results to each process. To solve this problem, Python multiprocessing introduces the RawArray class, which provides the ability to split a single data array between processes. I don’t know exactly what is the basis of RawArray. It seems to me that these are memory mapped files.
The solution code is as follows:
def mpnpGetR_worker(job):
start, stop = job
p = np.reshape(np.frombuffer(mp_share.p), (-1, 3))
q = np.reshape(np.frombuffer(mp_share.q), (3, -1))
R = np.reshape(np.frombuffer(mp_share.R), (p.shape[0], q.shape[1]))
Rx = p[start:stop, 0:1] - q[0:1]
Ry = p[start:stop, 1:2] - q[1:2]
Rz = p[start:stop, 2:3] - q[2:3]
R[start:stop, :] = 1 / (1 + np.sqrt(Rx * Rx + Ry * Ry + Rz * Rz))
def mpnpGetR(p, q):
nP, nQ = p.shape[0], q.shape[1]
sh_p = mp.RawArray(ctypes.c_double, p.ravel())
sh_q = mp.RawArray(ctypes.c_double, q.ravel())
sh_R = mp.RawArray(ctypes.c_double, nP * nQ)
nCPU = 4
jobs = utils.generateJobs(nP, nCPU)
pool = mp.Pool(processes=nCPU, initializer=mp_init, initargs=(sh_p, sh_q, sh_R))
pool.map(mpnpGetR_worker, jobs, chunksize=1)
R = np.reshape(np.frombuffer(sh_R), (nP, nQ))
return R
We create divided arrays for the input data and the output matrix, create a pool of processes according to the number of cores, divide the task into subtasks and solve in parallel.
Results:
| Multiprocessor numpy | 795 ms |
This is where the solutions for parallel programming known to me using only Python are over. Further, as much as we would not like, to get rid of the GIL we will have to go down to the C ++ level. But this one is not as scary as it seems.
4 Cython
Cython [3] is a Python extension that allows you to embed C instructions in Python code. Thus, we can take the Python code and add a few instructions to significantly speed up performance bottlenecks. Cython modules are converted to C code and then compiled into Python modules. The code for solving our problem in Cython is as follows:
Uniprocessor Cython:
@cython.boundscheck(False)
@cython.wraparound(False)
def spcyGetR(pp, pq):
pR = np.empty((pp.shape[0], pq.shape[1]))
cdef int i, j, k
cdef int nP = pp.shape[0]
cdef int nQ = pq.shape[1]
cdef double[:, :] p = pp
cdef double[:, :] q = pq
cdef double[:, :] R = pR
cdef double rx, ry, rz
with nogil:
for i in xrange(nP):
for j in xrange(nQ):
rx = p[i, 0] - q[0, j]
ry = p[i, 1] - q[1, j]
rz = p[i, 2] - q[2, j]
R[i, j] = 1 / (1 + sqrt(rx * rx + ry * ry + rz * rz))
return R
Multiprocessor Cython:
@cython.boundscheck(False)
@cython.wraparound(False)
def mpcyGetR(pp, pq):
pR = np.empty((pp.shape[0], pq.shape[1]))
cdef int i, j, k
cdef int nP = pp.shape[0]
cdef int nQ = pq.shape[1]
cdef double[:, :] p = pp
cdef double[:, :] q = pq
cdef double[:, :] R = pR
cdef double rx, ry, rz
with nogil, parallel():
for i in prange(nP, schedule='guided'):
for j in xrange(nQ):
rx = p[i, 0] - q[0, j]
ry = p[i, 1] - q[1, j]
rz = p[i, 2] - q[2, j]
R[i, j] = 1 / (1 + sqrt(rx * rx + ry * ry + rz * rz))
return R
If we compare this code with a pure Python implementation, all we had to do was just specify the types for the variables used. GIL is released in one line. A parallel loop is organized by a prange statement instead of an xrange. In my opinion, it is quite simple and beautiful!
Results:
| Uniprocessor Cython | 255 ms |
| Multiprocessor Cython | 75 ms |
5 numba
Numba [4] a fairly new library, is in active development. The idea here is about the same as in Cython - an attempt to go down to the C ++ level in Python code. But the idea is implemented much more elegantly.
Numba is based on LLVM compilers that allow compilation directly during program execution (JIT compilation). For example, to compile any procedure in Python, just add the jit annotation. Moreover, annotations allow you to specify the types of input / output data, which makes JIT compilation significantly more efficient.
The code for implementing the task is as follows.
Uniprocessor Numba:
@jit(double[:, :](double[:, :], double[:, :]))
def spnbGetR(p, q):
nP = p.shape[0]
nQ = q.shape[1]
R = np.empty((nP, nQ))
for i in xrange(nP):
for j in xrange(nQ):
rx = p[i, 0] - q[0, j]
ry = p[i, 1] - q[1, j]
rz = p[i, 2] - q[2, j]
R[i, j] = 1 / (1 + sqrt(rx * rx + ry * ry + rz * rz))
return R
Multiprocessor Numba:
def makeWorker():
savethread = pythonapi.PyEval_SaveThread
savethread.argtypes = []
savethread.restype = c_void_p
restorethread = pythonapi.PyEval_RestoreThread
restorethread.argtypes = [c_void_p]
restorethread.restype = None
def worker(p, q, R, job):
threadstate = savethread()
nQ = q.shape[1]
for i in xrange(job[0], job[1]):
for j in xrange(nQ):
rx = p[i, 0] - q[0, j]
ry = p[i, 1] - q[1, j]
rz = p[i, 2] - q[2, j]
R[i, j] = 1 / (1 + sqrt(rx * rx + ry * ry + rz * rz))
restorethread(threadstate)
signature = void(double[:, :], double[:, :], double[:, :], int64[:])
worker_ext = jit(signature, nopython=True)(worker)
return worker_ext
def mpnbGetR(p, q):
nP, nQ = p.shape[0], q.shape[1]
R = np.empty((nP, nQ))
nCPU = utils.getCPUCount()
jobs = utils.generateJobs(nP, nCPU)
worker_ext = makeWorker()
threads = [threading.Thread(target=worker_ext, args=(p, q, R, job)) for job in jobs]
for thread in threads:
thread.start()
for thread in threads:
thread.join()
return R
Compared to pure Python, only one annotation is added to a single-processor solution on Numba! The multiprocessor version, unfortunately, is not so beautiful. It requires organizing a pool of threads, manually giving GIL. In previous releases of Numba, there was an attempt to implement a parallel loop with a single instruction, but due to stability issues in subsequent releases, this feature was removed. I am sure that over time this opportunity will be repaired.
Execution Results:
| Uniprocessor Numba | 359 ms |
| Multiprocessor numba | 180 ms |
conclusions
I want to illustrate the results with the following diagrams:
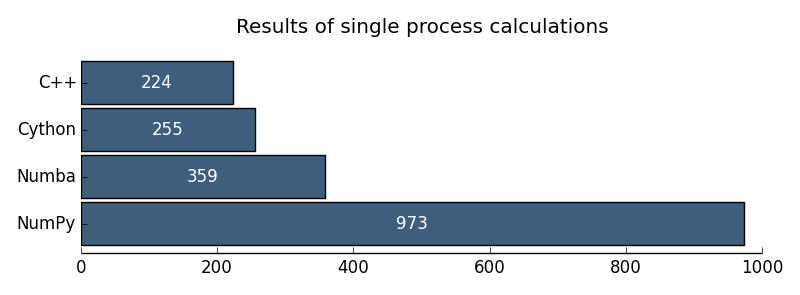
Fig. 1. The results of uniprocessor computing
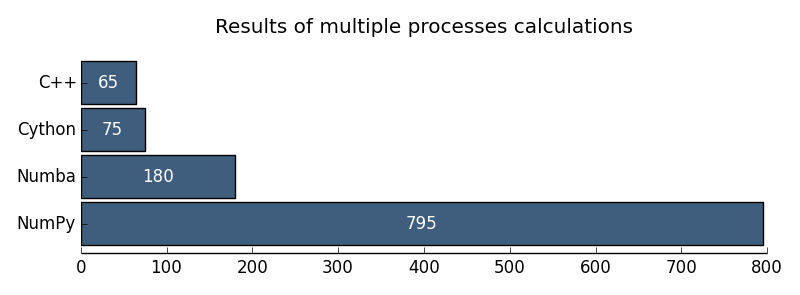
Fig. 2. The results of multiprocessor calculations
It seems to me that the GIL problems in Python for numerical calculations are practically overcome. So far, I would recommend Cython as a parallel computing technology. But I would really take a close look at Numba.
References
[1] Scientific Python: scipy.org
[2] Full source code for the tests: github.com/alec-kalinin/open-nuance
[3] Cython: cython.org
[4] Numba: numba.pydata.org
PS In the comments " @chersaya "correctly pointed out another way of parallel computing. This is the use of the numexpr library. Numexpr uses its own virtual machine written in C and its own JIT compiler. This allows him to accept simple mathematical expressions as a string, compile and quickly calculate.
Usage example:
import numpy as np
import numexpr as ne
a = np.arange(1e6)
b = np.arange(1e6)
result = ne.evaluate("sin(a) + arcsinh(a/b)")
