rokuz July 5, 2014 at 11:09

Fur rendering using Shells and Fins algorithm

Hello, Habr! My today's post on programming graphics will not be as voluminous as the previous ones. In almost any difficult business, sometimes there is a place for frivolous ones, and today we will render seals. More precisely, I want to talk about the implementation of the Shells and Fins (SAF) fur rendering algorithm, traditionally for Direct3D 11 and OpenGL 4. For details, I ask for cat.

The SAF fur rendering algorithm, as the name implies, consists of 2 parts: rendering of shells and rendering of fins. These names may seem funny to some, but they fully reflect what is created by the algorithm to create the illusion of a fleecy surface. For more details on the implementation of the algorithm for Direct3D 10, see the article and the NVidia demo, my demo for Direct3D 11 and OpenGL 4 can be foundhere . The project is called Demo_Fur. To build you will need Visual Studio 2012/2013 and CMake .

Shells and Fins Algorithm

The fur consists of a huge number of hairs, drawing each of which separately at the moment is not possible in real time, although NVidia had some attempts . In order to create the illusion of a fleecy surface, technology is applied that is somewhat reminiscent of voxel rendering. A three-dimensional texture is prepared, which is a small area of the fur surface. Each voxel in it determines the probability of the villi passing through itself, which from a graphical point of view determines the value of transparency at one point or another during rendering. Such a three-dimensional texture can be generated (one of the methods described here) A logical question arises as to how to render this texture. To do this, “shells” are drawn around the geometry, i.e. copies of the original geometry, formed by scaling this geometry by small values. It turns out a kind of nesting doll, on each layer of which a layer of a three-dimensional fur texture is superimposed. Layers are drawn sequentially with alpha blending enabled, which results in some illusion of hairiness. However, this is not enough to make the material resemble fur. To achieve the goal, you need to choose the right lighting model.
The fur belongs to the category of pronounced anisotropic materials. Classic lighting models (e.g. Blinn-Phong model) consider surfaces as isotropic, i.e. surface properties are independent of its orientation. In practice, this means that when the plane rotates around its normal, the nature of the lighting does not change. Lighting models of this class use the angle between the normal and the direction of light incidence to calculate the shading. Anisotropic lighting models use tangents (vectors perpendicular to the normals, which together with the normals and binormals form a basis) to calculate the illumination. Read more about anisotropic lighting here .
Anisotropic lighting is calculated separately for each fur layer. The tangent values at one point or another on the surface are determined using the tangent map. The tangent map is formed almost in the same way as the well-knownnormal map . In the case of a fur texture, the tangent vector will be the normalized villi direction. Thus, the three-dimensional texture of the fur will contain 4 channels. The packed tangent vector will be stored in RGB, the alpha channel will contain the probability of the villus passing through this point. Add to this an account of the self-shadowing of the fur and get fairly realistic looking material.
The illusion will be broken if a person carefully looks at the external edges of the object. At certain angles between faces in a situation where one face is visible and the other is not, layers of the fur may be invisible to the observer. To avoid this situation, additional geometry is formed on such edges, which extends along their normals. The result is somewhat reminiscent of fins in fish, which led to the second part of the name of the algorithm.

Implementation on Direct3D 11 and OpenGL 4

The implementation on both APIs is generally identical, only minor details differ. We will render according to the following scheme:

Rendering of non-furry parts of the scene. My demo uses the standard Blinn-Fong lighting model for such parts.

Rendering fins. We will implement geometry stretching using a geometric shader. To understand whether it is necessary to extend an edge between two polygons, it is necessary to determine whether this edge is external with respect to the object. A sign of this will be the values of the angles between the normals to the polygons and the normalized vision vector. If these values have a different sign, then the edge will be external, and therefore it must be extended. Geometric shaders in Direct3D and OpenGL can work with a limited number of primitives. We need to simultaneously process 2 adjacent polygons with one common edge. To represent this structure, 4 vertices are minimally necessary, which is clearly shown in the figure below to the left.

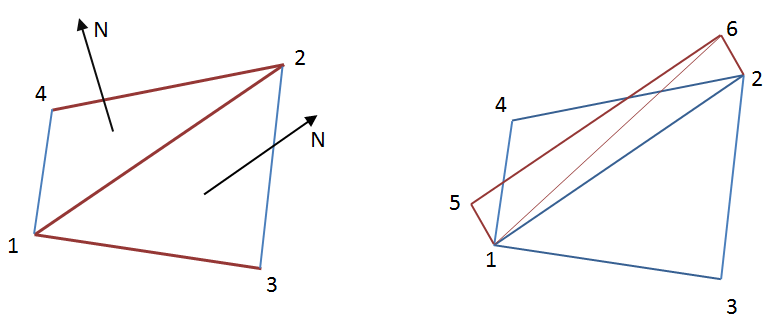
The right side of the figure shows the extension of the common rib 1-2 and the formation of two new polygons 1-5-6 and 1-6-2.
The primitive, which consists of 4 vertices, is D3D_PRIMITIVE_TOPOLOGY_LINELIST_ADJ (GL_LINES_ADJACENCY in OpenGL). In order to use it, we need to prepare a special index buffer. Such a buffer is simple enough to build if there is data on the adjacency of triangles in the 3D model. The index buffer will contain groups of 4 indexes describing 2 adjacent triangles.
It is important to note here that not every model can easily obtain adjacency data. For most smoothed models, this is not a problem, however, at the borders of the smoothing groups, the vertices are usually duplicated to achieve the correct lighting. This means the virtual absence of adjacency in the index buffer in the presence of visual adjacency. In this case, it is necessary to search for adjacent triangles, being guided not only by indices, but also by the actual arrangement of vertices in space. This task is no longer so trivial, since in this case as many triangles as possible can be divided into one face.
Geometric shaders for pulling “fins” are shown below under the spoilers.

HLSL Geometric Shader for Direct3D 11

#include 
struct GS_INPUT
{
    float4 position : SV_POSITION;
	float2 uv0 : TEXCOORD0;
	float3 normal : TEXCOORD1;
};
struct GS_OUTPUT
{
    float4 position : SV_POSITION;
	float3 uv0 : TEXCOORD0;
};
texture2D furLengthMap : register(t0);
SamplerState defaultSampler : register(s0);
[maxvertexcount(6)]
void main(lineadj GS_INPUT pnt[4], inout TriangleStream triStream)
{
	float3 c1 = (pnt[0].position.xyz + pnt[1].position.xyz + pnt[2].position.xyz) / 3.0f;
	float3 c2 = (pnt[1].position.xyz + pnt[2].position.xyz + pnt[3].position.xyz) / 3.0f;
	float3 viewDirection1 = -normalize(viewPosition - c1);
	float3 viewDirection2 = -normalize(viewPosition - c2);
	float3 n1 = normalize(cross(pnt[0].position.xyz - pnt[1].position.xyz, pnt[2].position.xyz - pnt[1].position.xyz));
	float3 n2 = normalize(cross(pnt[1].position.xyz - pnt[2].position.xyz, pnt[3].position.xyz - pnt[2].position.xyz));
	float edge = dot(n1, viewDirection1) * dot(n2, viewDirection2);
	float furLen = furLengthMap.SampleLevel(defaultSampler, pnt[1].uv0, 0).r * FUR_LENGTH;
	if (edge > 0 && furLen > 1e-3)
	{
		GS_OUTPUT p[4];
		p[0].position = mul(pnt[1].position, modelViewProjection);
		p[0].uv0 = float3(pnt[1].uv0, 0);
		p[1].position = mul(pnt[2].position, modelViewProjection);
		p[1].uv0 = float3(pnt[2].uv0, 0);
		p[2].position = mul(float4(pnt[1].position.xyz + pnt[1].normal * furLen, 1), modelViewProjection);
		p[2].uv0 = float3(pnt[1].uv0, 1);
		p[3].position = mul(float4(pnt[2].position.xyz + pnt[2].normal * furLen, 1), modelViewProjection);
		p[3].uv0 = float3(pnt[2].uv0, 1);
		triStream.Append(p[2]);
		triStream.Append(p[1]);
		triStream.Append(p[0]);
		triStream.RestartStrip();
		triStream.Append(p[1]);
		triStream.Append(p[2]);
		triStream.Append(p[3]);
		triStream.RestartStrip();
	}
}

GLSL Geometric Shader for OpenGL 4.3

#version 430 core
layout(lines_adjacency) in;
layout(triangle_strip, max_vertices = 6) out;
in VS_OUTPUT
{
	vec2 uv0;
	vec3 normal;
} gsinput[];
out vec3 texcoords;
const float FUR_LAYERS = 16.0f;
const float FUR_LENGTH = 0.03f;
uniform mat4 modelViewProjectionMatrix;
uniform sampler2D furLengthMap;
uniform vec3 viewPosition;
void main()
{
	vec3 c1 = (gl_in[0].gl_Position.xyz + gl_in[1].gl_Position.xyz + gl_in[2].gl_Position.xyz) / 3.0f;
	vec3 c2 = (gl_in[1].gl_Position.xyz + gl_in[2].gl_Position.xyz + gl_in[3].gl_Position.xyz) / 3.0f;
	vec3 viewDirection1 = -normalize(viewPosition - c1);
	vec3 viewDirection2 = -normalize(viewPosition - c2);
	vec3 n1 = normalize(cross(gl_in[0].gl_Position.xyz - gl_in[1].gl_Position.xyz, gl_in[2].gl_Position.xyz - gl_in[1].gl_Position.xyz));
	vec3 n2 = normalize(cross(gl_in[1].gl_Position.xyz - gl_in[2].gl_Position.xyz, gl_in[3].gl_Position.xyz - gl_in[2].gl_Position.xyz));
	float edge = dot(n1, viewDirection1) * dot(n2, viewDirection2);
	float furLen = texture(furLengthMap, gsinput[1].uv0).r * FUR_LENGTH;
	vec4 p[4];
	vec3 uv[4];
	if (edge > 0 && furLen > 1e-3)
	{
		p[0] = modelViewProjectionMatrix * vec4(gl_in[1].gl_Position.xyz, 1);
		uv[0] = vec3(gsinput[1].uv0, 0);
		p[1] = modelViewProjectionMatrix * vec4(gl_in[2].gl_Position.xyz, 1);
		uv[1] = vec3(gsinput[2].uv0, 0);
		p[2] = modelViewProjectionMatrix * vec4(gl_in[1].gl_Position.xyz + gsinput[1].normal * furLen, 1);
		uv[2] = vec3(gsinput[1].uv0, FUR_LAYERS - 1);
		p[3] = modelViewProjectionMatrix * vec4(gl_in[2].gl_Position.xyz + gsinput[2].normal * furLen, 1);
		uv[3] = vec3(gsinput[2].uv0, FUR_LAYERS - 1);
		gl_Position = p[2]; texcoords = uv[2];
		EmitVertex();
		gl_Position = p[1]; texcoords = uv[1];
		EmitVertex();
		gl_Position = p[0]; texcoords = uv[0];
		EmitVertex();
		EndPrimitive();
		gl_Position = p[1]; texcoords = uv[1];
		EmitVertex();
		gl_Position = p[2]; texcoords = uv[2];
		EmitVertex();
		gl_Position = p[3]; texcoords = uv[3];
		EmitVertex();
		EndPrimitive();
	}
}

Carapace rendering. Obviously, to obtain the proper number of layers of fur, the geometry must be drawn several times. For repeated drawing of geometry we will use hardware instancing. In order to determine in the shader which particular layer of the fur is drawn, it is enough to use the semantics of SV_InstanceID in Direct3D and the variable gl_InstanceID in OpenGL.
To illuminate the fur, I used the Kajiya-Kay anisotropic model. An important detail was the use of a special texture to set the length of the fur. This texture is necessary to prevent the appearance of long fur in unexpected places (for example, around the eyes of a cat). Pixel and fragment shaders for calculating fur lighting are shown below under the spoilers.

HLSL Pixel Shader for Direct3D 11

#include 
struct PS_INPUT
{
	float4 position : SV_POSITION;
	float3 uv0 : TEXCOORD0;
	float3 tangent : TEXCOORD1;
	float3 normal : TEXCOORD2;
	float3 worldPos : TEXCOORD3;
};
texture2D diffuseMap : register(t1);
texture3D furMap : register(t2);
SamplerState defaultSampler : register(s0);
float4 main(PS_INPUT input) : SV_TARGET
{
	const float specPower = 30.0;
	float3 coords = input.uv0 * float3(FUR_SCALE, FUR_SCALE, 1.0f);
	float4 fur = furMap.Sample(defaultSampler, coords);
	clip(fur.a - 0.01);
	float4 outputColor = float4(0, 0, 0, 0);
	outputColor.a = fur.a * (1.0 - input.uv0.z);
	outputColor.rgb = diffuseMap.Sample(defaultSampler, input.uv0.xy).rgb;
	float3 viewDirection = normalize(input.worldPos - viewPosition);
	float3x3 ts = float3x3(input.tangent, cross(input.normal, input.tangent), input.normal);
	float3 tangentVector = normalize((fur.rgb - 0.5f) * 2.0f);
	tangentVector = normalize(mul(tangentVector, ts));
	float TdotL = dot(tangentVector, light.direction);
	float TdotE = dot(tangentVector, viewDirection);
	float sinTL = sqrt(1 - TdotL * TdotL);
	float sinTE = sqrt(1 - TdotE * TdotE);
	outputColor.xyz = light.ambientColor * outputColor.rgb +
					  light.diffuseColor * (1.0 - sinTL) * outputColor.rgb +
					  light.specularColor * pow(abs((TdotL * TdotE + sinTL * sinTE)), specPower) * FUR_SPECULAR_POWER;
	float shadow = input.uv0.z * (1.0f - FUR_SELF_SHADOWING) + FUR_SELF_SHADOWING;
	outputColor.rgb *= shadow;
	return outputColor;
}

GLSL fragment shader for OpenGL 4.3

#version 430 core
in VS_OUTPUT
{
	vec3 uv0;
	vec3 normal;
	vec3 tangent;
	vec3 worldPos;
} psinput;
out vec4 outputColor;
const float FUR_LAYERS = 16.0f;
const float FUR_SELF_SHADOWING = 0.9f;
const float FUR_SCALE = 50.0f;
const float FUR_SPECULAR_POWER = 0.35f;
// lights
struct LightData
{
	vec3 position;
	uint lightType;
	vec3 direction;
	float falloff;
	vec3 diffuseColor;
	float angle;
	vec3 ambientColor;
	uint dummy;
	vec3 specularColor;
	uint dummy2;
};
layout(std430) buffer lightsDataBuffer
{
    LightData lightsData[];
};
uniform sampler2D diffuseMap;
uniform sampler2DArray furMap;
uniform vec3 viewPosition;
void main()
{
	const float specPower = 30.0;
	vec3 coords = psinput.uv0 * vec3(FUR_SCALE, FUR_SCALE, 1.0);
	vec4 fur = texture(furMap, coords);
	if (fur.a < 0.01) discard;
	float d = psinput.uv0.z / FUR_LAYERS;
	outputColor = vec4(texture(diffuseMap, psinput.uv0.xy).rgb, fur.a * (1.0 - d));
	vec3 viewDirection = normalize(psinput.worldPos - viewPosition);
	vec3 tangentVector = normalize((fur.rgb - 0.5) * 2.0);
	mat3 ts = mat3(psinput.tangent, cross(psinput.normal, psinput.tangent), psinput.normal);
	tangentVector = normalize(ts * tangentVector);
	float TdotL = dot(tangentVector, lightsData[0].direction);
	float TdotE = dot(tangentVector, viewDirection);
	float sinTL = sqrt(1 - TdotL * TdotL);
	float sinTE = sqrt(1 - TdotE * TdotE);
	outputColor.rgb = lightsData[0].ambientColor * outputColor.rgb +
					  lightsData[0].diffuseColor * (1.0 - sinTL) * outputColor.rgb +
					  lightsData[0].specularColor * pow(abs((TdotL * TdotE + sinTL * sinTE)), specPower) * FUR_SPECULAR_POWER;
	float shadow = d * (1.0 - FUR_SELF_SHADOWING) + FUR_SELF_SHADOWING;
	outputColor.rgb *= shadow;
}

As a result, we can get such cats.

For comparison, the picture on the right shows the rendering of a cat using the Blinn-Fong model using normal maps.

Performance

The SAF algorithm is quite simple to implement, but it can significantly complicate the life of the video card. Each model will be drawn several times to obtain a given number of layers of fur (I used 16 layers). In the case of complex geometry, this can give a significant drawdown in performance. In the used cat model, the part covered with fur occupies about 3000 polygons, therefore, about 48000 polygons will be drawn to render the skin. When drawing “fins”, not the simplest geometric shader is used, which can also affect a highly detailed model.
Measurements of performance were carried out on a computer with the following configuration: AMD Phenom II X4 970 3.79GHz, 16Gb RAM, AMD Radeon HD 7700 Series, OS Windows 8.1.

Average frame time. 1920x1080 / MSAA 8x / full screen

API / Number of Seals	1	25	100
Direct3D 11	2.73615ms	14.3022ms	42.8362ms
Opengl 4.3	2.5748ms	13.4807ms	34.2388ms

In total, the implementation on OpenGL 4 approximately corresponds to the implementation on Direct3D 11 in terms of performance on average and a small number of objects. On a large number of objects, the implementation on OpenGL is somewhat faster.

Conclusion

The SAF algorithm is one of the few ways to implement fur in interactive rendering. However, it cannot be said that the algorithm is necessary for the vast majority of games. To date, a similar level of quality (and possibly even higher) is achieved with the help of art and the skillful hands of a graphic designer. The combination of translucent planes with well-chosen textures for representing hair and fur is the standard of modern games, and the considered algorithm and its variations are rather the destiny of future games.

Tags:

Fur rendering using Shells and Fins algorithm

Shells and Fins Algorithm

Implementation on Direct3D 11 and OpenGL 4

Performance

Conclusion

Also popular now: