How Minkowski played in Flappy Bird

Many have tried playing Flappy Bird. Few people manage to fly in 50 pipes, very few reach hundreds or two. Some tried to create a bot, including on a habr . Surprisingly, even the most successful bot, which can be found on the Internet, the results are not very impressive - something about 160 points . The question arises, is it possible to play Flappy Bird in general indefinitely? Or is it always possible with some, albeit small, probability that there will be a sequence of obstacles that even an experienced player / ideal bot cannot overcome?
And here mathematics comes to the rescue. Let's find a winning strategy for Flappy Bird.
Model
We describe the mathematical model of the game. Our playing field is a plane. There is a bird - a square with sides of length w parallel to the coordinate axes. There are obstacles - pipes - vertical stripes of width w tube with horizontal openings of height h gap . The horizontal distance between two adjacent obstacles is fixed and equal to Δ tube . The location of the horizontal opening for each pipe is random (evenly in a certain range). In addition there is a floor - a horizontal line f. Sex is also an obstacle. Picture:
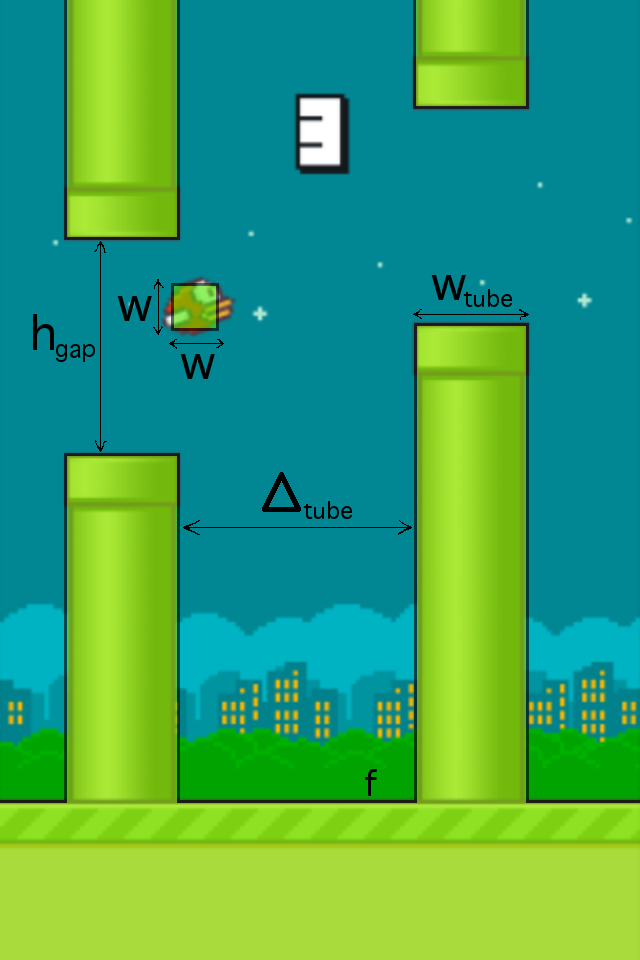
The horizontal speed of the bird is constant and equal to v x . Gravity also acts on the bird, giving it vertical acceleration g. Initially, the bird’s vertical speed is 0. At each time, the player can tap, that is, make the bird’s vertical speed equal v jump . In addition, a kind of air resistance acts on the bird - its vertical speed is limited from below by the constant v fall . In fact, this means that after each tap, the bird moves along a parabola, which at some point passes into a straight line. The trajectory along which the bird moves after tapa will be called padabola (fall parabola). It looks like this:
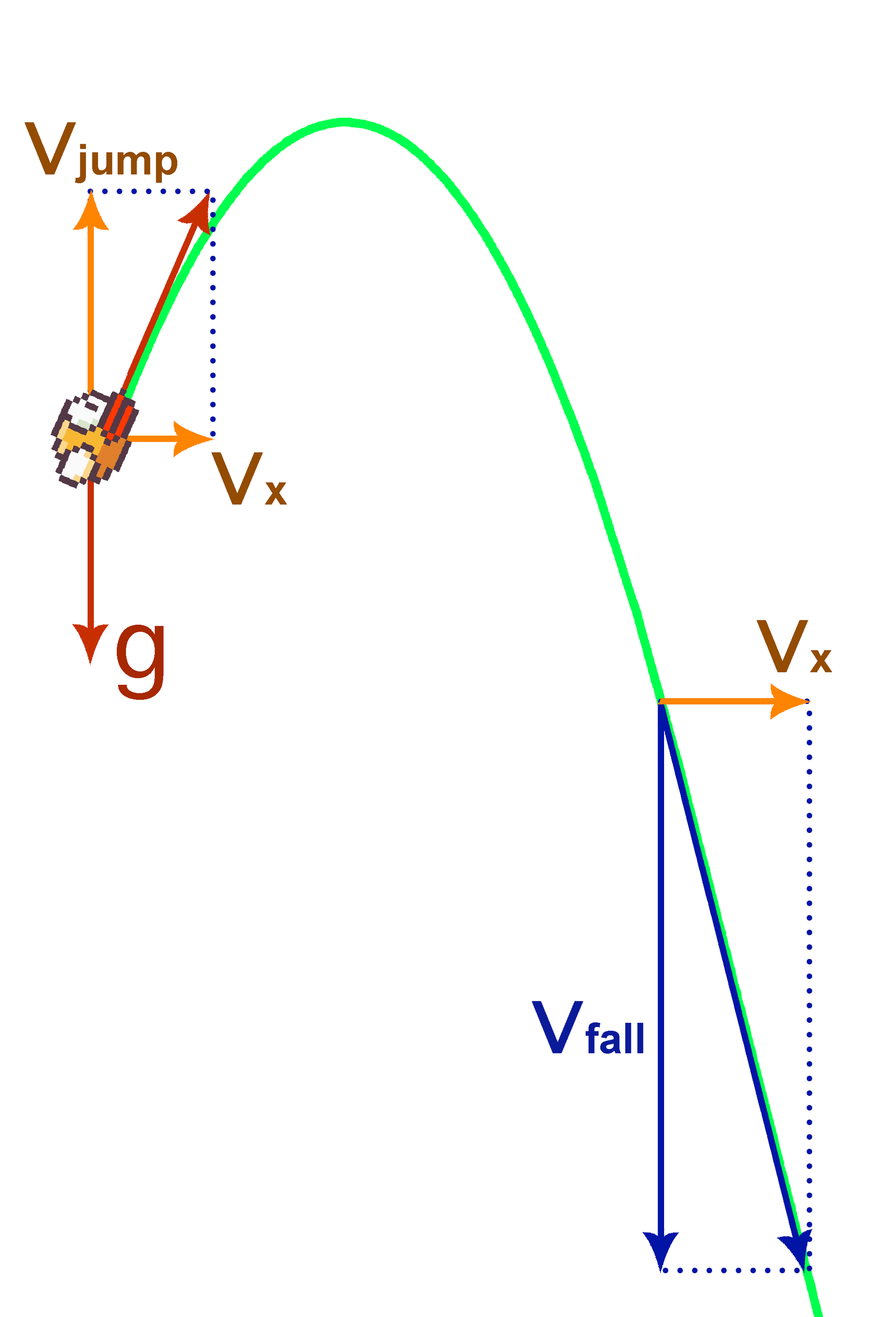
The game ends when the bird touches the obstacle. The player’s task is to maximize the distance traveled.
Before moving on to the strategy of passing, let’s do one trick. It is not very convenient to analyze the intersection of a square bird with obstacles. But it turns out that it’s easy to switch to the equivalent model, in which the bird is a point. To do this, it is enough to “blow off” the bird to the size of a point (the center of the initial square), while simultaneously “inflating” the obstacles. In this case, the initial square intersects with obstacles if and only if a new point bird lies in a swollen obstacle. Picture:
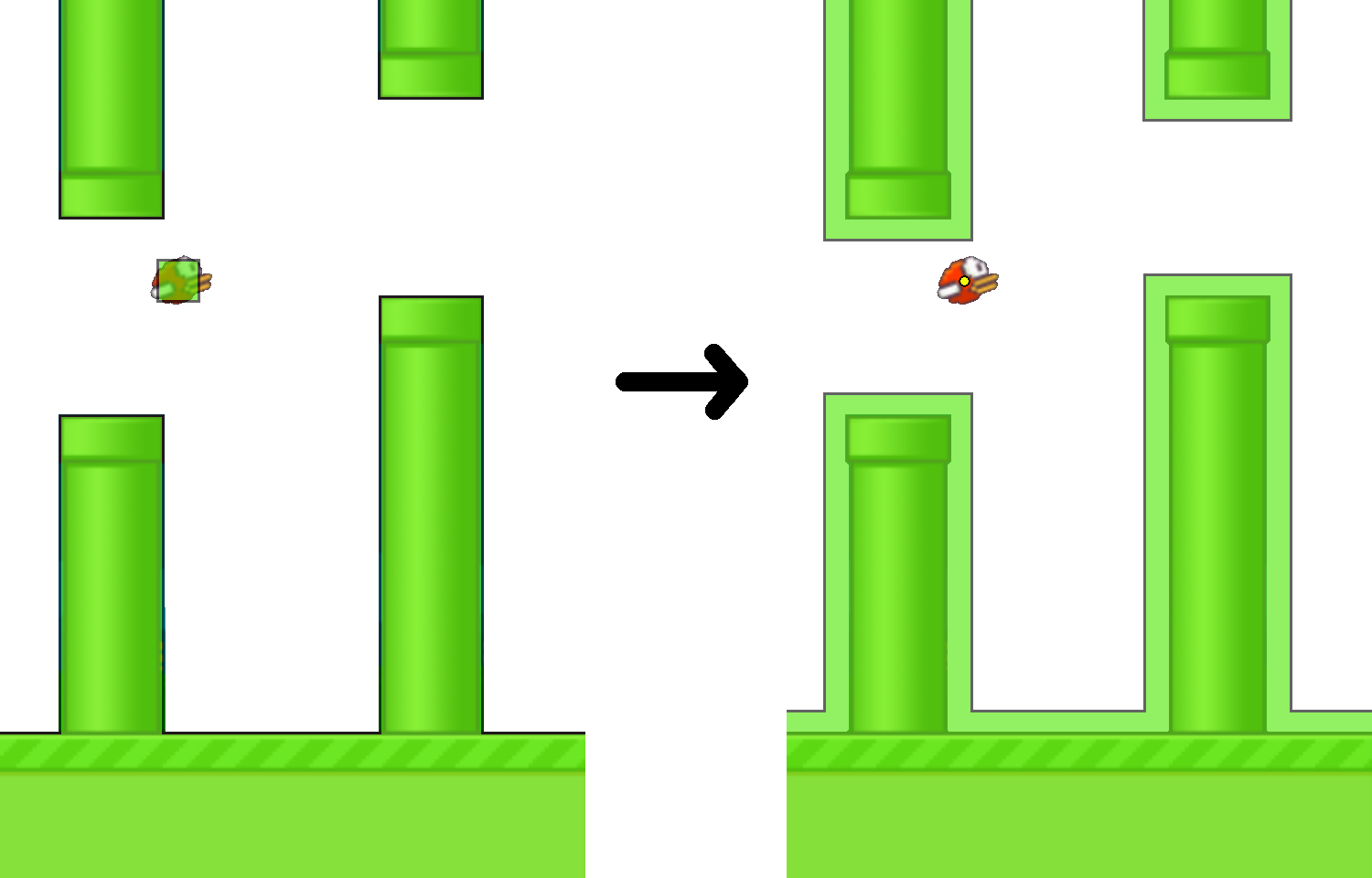
Scientifically, the result of "bloating" obstacles is called the Minkowski sum.
Minkowski sum
Wikipedia reports:
The Minkowski sum of two subsets A and B of a linear space V is the set C consisting of the sums of all possible vectors from A and B: C = {c | c = a + b, a∈A, b∈B}
From the everyday point of view, we can assume that the Minkowski sum of figures A and B is a figure obtained if a figure A is attached to each point B - see the right figure.
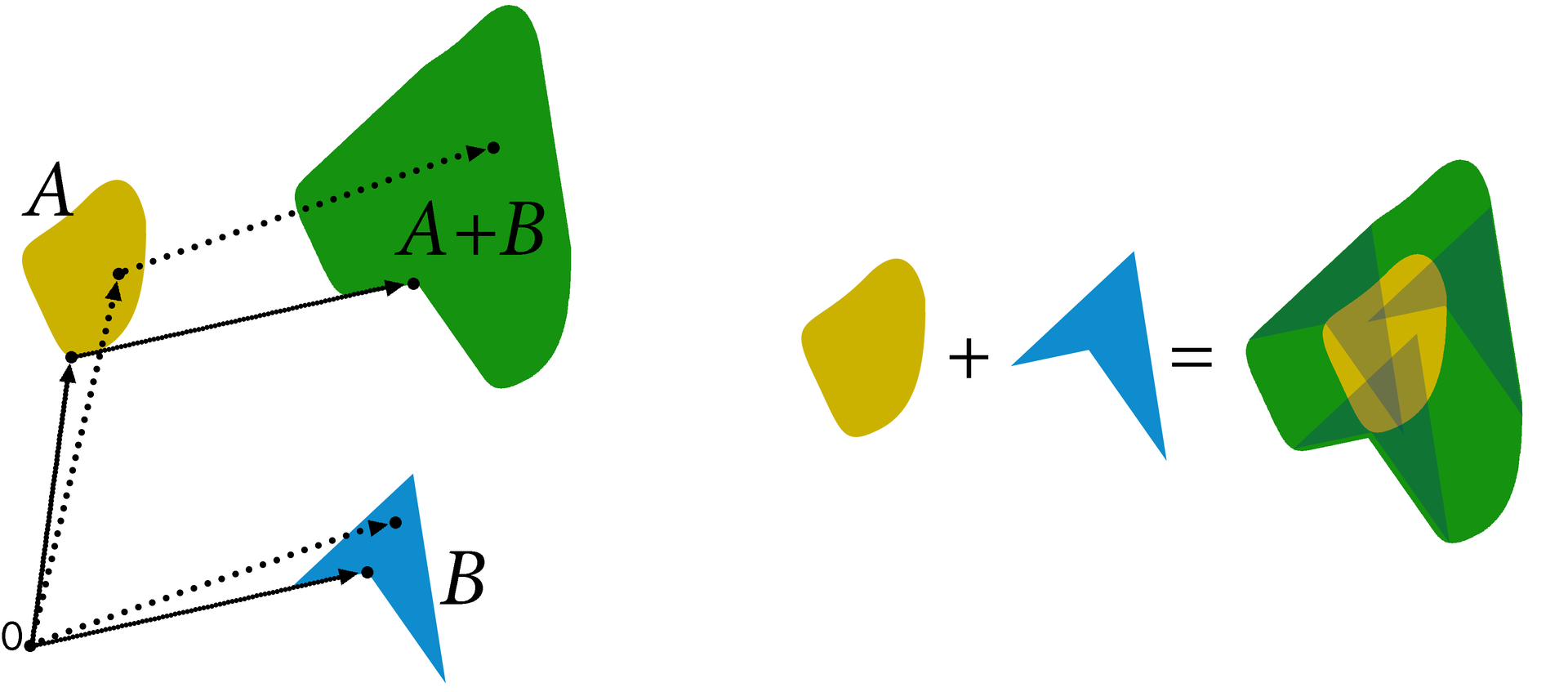
Reverse padabola
We will solve the auxiliary problem: where should the bird be so that after the tap it flies through the given point A? More precisely, it is required to find the geometrical location of the points such that the padabol drawn from them pass through the fixed point A. See the middle figure. Let v⃗ be an arbitrary vector connecting the beginning of a padabola with one of its points. It is easy to see that after the tap at point A-v⃗, the bird flies through point A. That is, A-v⃗ belongs to the desired geometric location of the points. Moreover, taking all sorts of vectors v⃗, we get all the desired points. But what is the set of points of the form A-v⃗, where v is the radius of the vector to one of the points of the padabola? This is a path that is centrally symmetric to the padole after reflection relative to point A. With the picture, by the way, it’s clearer:
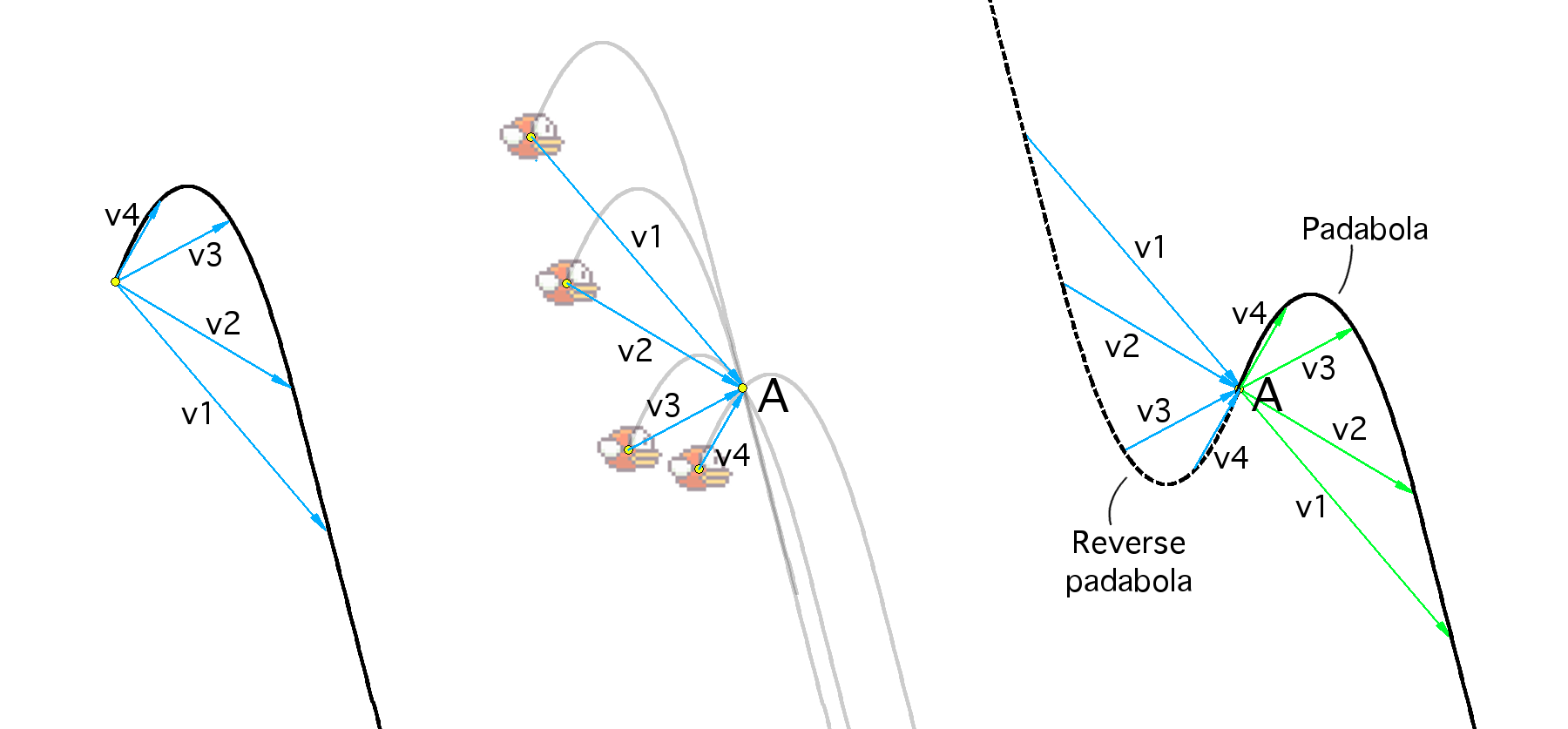
You can summarize the problem: where do you need to tap to fly through a given area S? Based on the foregoing, the answer is the sum of the Minkowski region S and the reverse padadola:
Upper obstacles
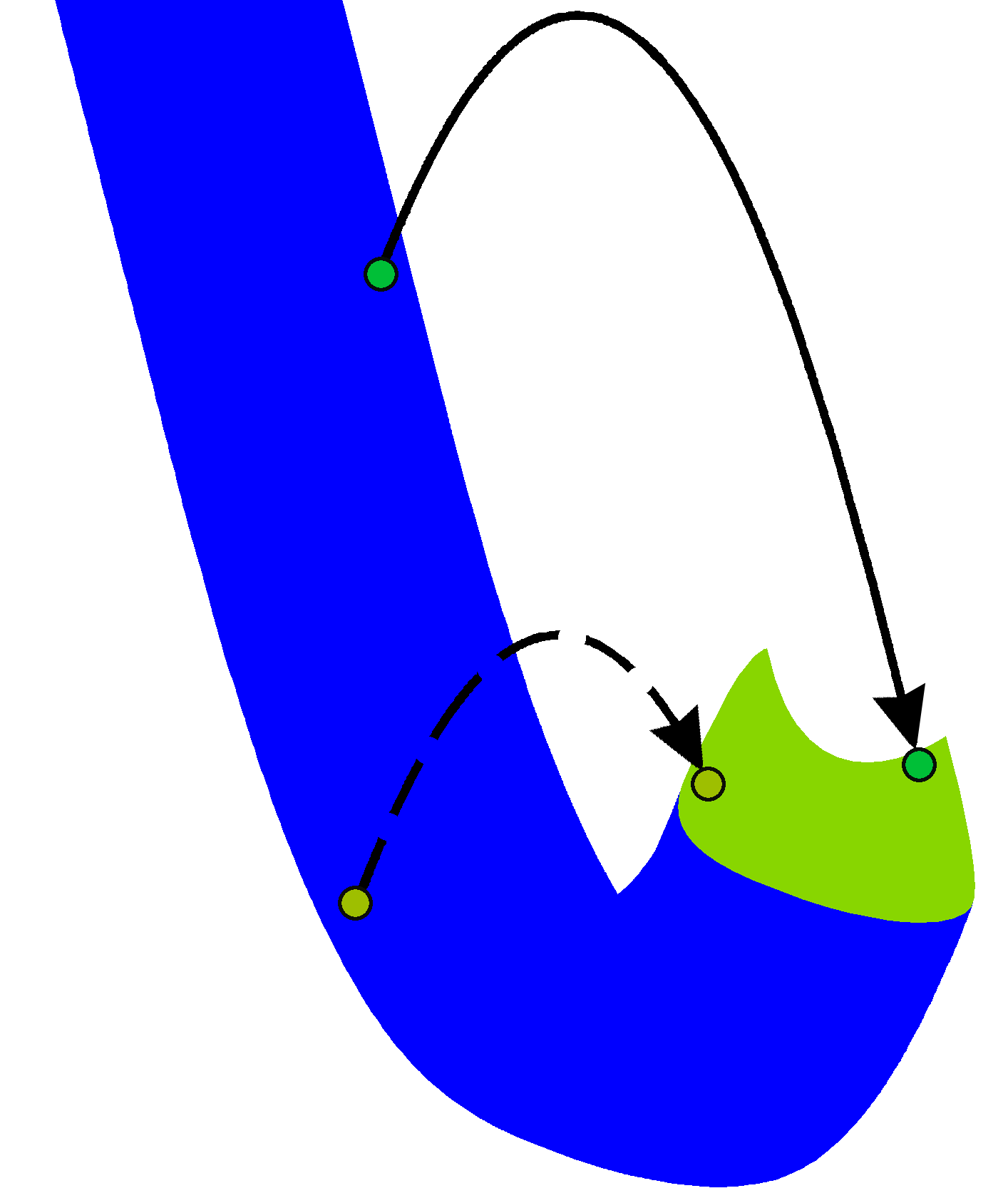
Finally, we turn to the main task - finding a winning strategy. Only first we solve it in a simplified case. Let the model have no lower halves of pipes and floor. That is, we have only the upper parts of the obstacles. Consider the freestanding upper half of the pipe. Let the bird begin its journey somewhere far to the left of this obstacle. Suppose, at some point in time, a bird crashed into a pipe. As we know from the previous paragraph, this means that a tap was made in the area obtained by adding the reverse padabola to the obstruction. Color the resulting area in blue. Picture:

Note that if a player taped at any point in the blue area, then the corresponding padabola first intersects with the obstacle and only then leaves the blue area. In other words, the player will be forced to either lose or tap again in the blue area. Well, since a single blue region is limited to the right, flying in it to infinity will not work, and, in the end, the bird will die. Thus, tap in the blue area always leads to defeat. Moreover, tapas outside the blue area cannot lead to loss - without a tap in the blue area you cannot crash into the upper obstacle, and there is nothing more to prevent the bird from flying.
As a result, for the case of upper obstacles alone, we obtain the following statement.
Statement . If the bird began its flight outside the pool of blue areas, then endless winning strategies exist. And all winning strategies are described as follows: outside the blue areas the player can make arbitrary decisions, in the blue areas the player cannot tap.
Lower obstacles
Now consider the case when only the lower halves of the pipes are present in the model. That is, there are no upper halves and sex. Again, consider a separate lower obstacle. Draw an AC beam through its upper left corner (point A), whose tilt angle is atan (v jump / v x ) - that is, a beam directed along the bird’s speed at the moment immediately after the tap. Let the bird be below the AC beam. Then, regardless of the player’s actions, she will not be able to rise with a vertical speed greater than v jump . Given the constant horizontal speed v x this leads to an inevitable collision with an obstacle, that is, a loss. Color the lower obstacle and the area below the AC beam in red. Here are the red slides obtained:
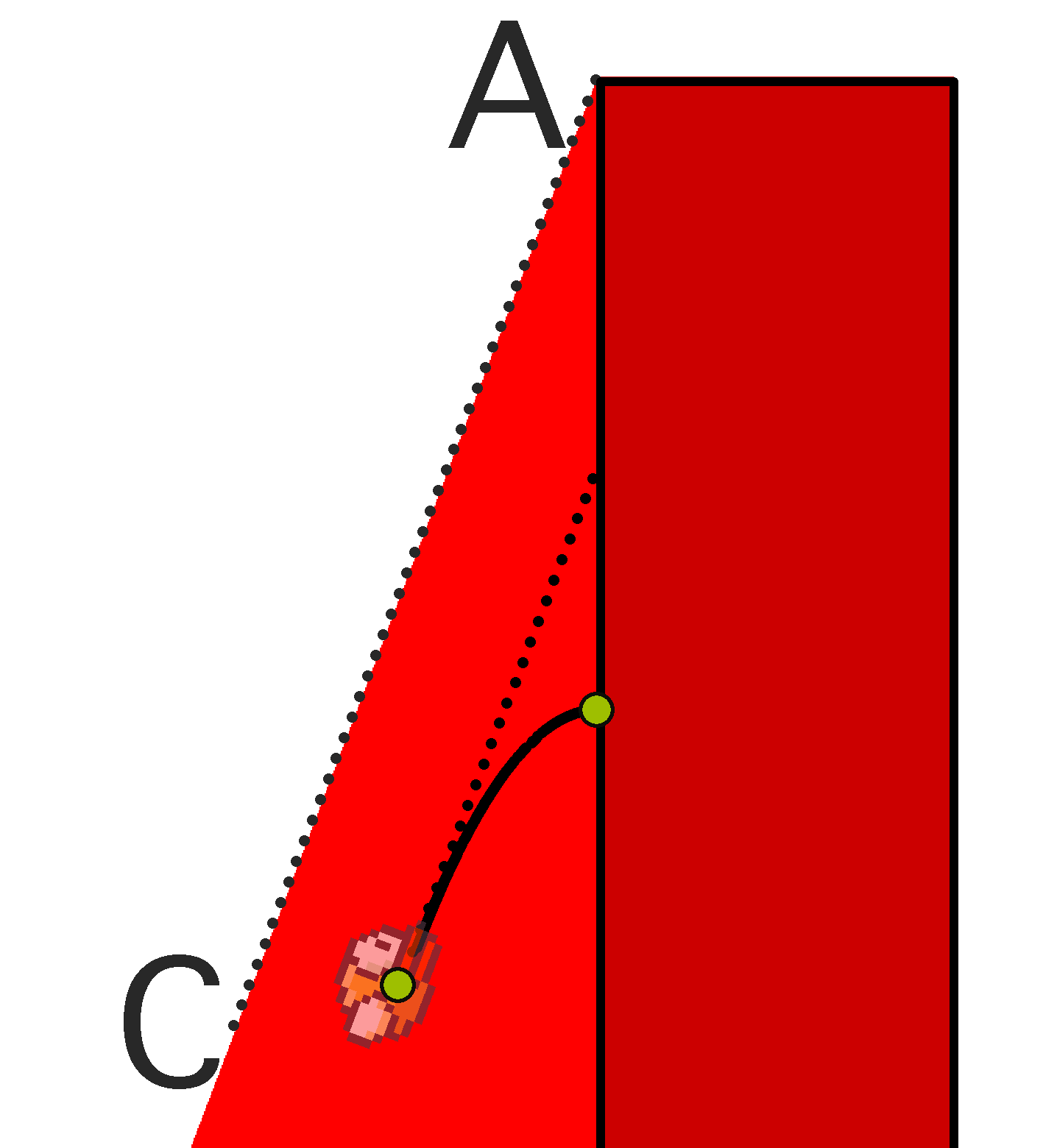
It turns out that with any winning strategy, the bird should not fall into the red areas. Moreover, if the bird is outside the red area at some point in time, then it can remain outside of it for an arbitrarily long time. Indeed, always when approaching the border of the red area, the player can start tapping often enough not to be in it.
Add gender. It is easy to see that the floor can be perceived as another red area in the form of a lower half-plane.
Thus, if only the lower obstacles and the floor are present, then it is true:
Statement . If the bird at the initial moment of time is outside the union of the red areas, then there are endless winning strategies. All winning strategies can be formulated as follows: outside the red area, the player can make any decisions, when approaching the red area, the player must tap.
All obstacles together
Consider the general situation. Let there be the upper halves of the pipes, and the lower, and the floor. The following is understandable:
Statement . If the union of blue areas does not intersect with the union of red and the bird is initially outside the blue and red areas, then there are winning strategies. Any winning strategy is described as follows: outside the blue and red areas, you can make any decisions, you cannot tap in the blue areas, and when you approach the red areas you need to tap.
The absence of intersections of blue and red areas for the existence of such a strategy is essential. Indeed, it may happen that a bird flying through the blue region comes close to the red border - in this case, if the player taps, then he will lose, if he does not tapping, he will also lose.
The question is, do blue and red areas intersect in a real game? It turns out that sometimes intersect. And this happens exactly in one case: when there is a sufficiently large difference in height down between the openings of two adjacent pipes.

Let us analyze this situation. Let the bird managed to fly through these pipes. So, at some point in time she crossed the segment AB. But this means that a tap was made in the area between the reverse padadol, drawn from points A and B. At the same time, this tap could not be made either in the blue region or in the red. Only the area shown in the figure in yellow remains.
That is, for the existence of a winning strategy, you need to be able to guarantee getting into the yellow area. All that remains is to do tap and the dangerous section will be overcome. In order to understand whether we can always get into the yellow area, add it with the reverse padadola - we get the area (green in the figure), which is enough to get in to reach the yellow one tap. Note that if at some point in time a tap is made at a point lying above the line Г, we will not be able to get into the yellow region. And vice versa, for any point below this border, we can always, by tapping a sufficient number of times in a row, climb into the green area, then, by tapping once, get into the yellow area and, accordingly, overcome the obstacle. In other words, the points located above the line G in our terminology should be painted blue. True, for the most part they are already blue, except for the curved triangle XYZ. Dye XYZ in blue. Now, to formulate a winning strategy, it remains to add the phrase: if the bird is in the yellow area, it is necessary to tap at least once before the bird leaves this area.
Note that the additional coloring of the triangle in blue could not add the intersections of the red and blue areas, and therefore did not affect the analysis of the patency of the game as a whole.
As a result, in the general case we get:
Statement . Let the bird at the initial moment of time be outside the blue and red areas. Then there are endless winning strategies. All such strategies can be described as follows: outside the blue and red areas, you can tap at any given time; in blue areas you can’t tap; when approaching red, you need to tap; Once in the yellow area, you need to tap at least once before exiting it.
It is interesting that the strategy of the species to start flying above a certain line and tapping as soon as the bird falls to it (for example, it would be logical to take the upper border of the red areas slightly shifted up), apparently there will be no winning line for any line.
Practice
All this is good, but I would like some practical results. We already saw hardcore bots on the hub, so we decided to make software. Quite by chance, at hand was the code of our clone called Tappinator, the physical model of which is quite close to the original game - they tried, measured. True, we have a round bird (although it may be round in Flappy Bird, but the difference is small, and it is easier to explain with the square one) and there are additional obstacles - inclined. This is how the obstacles for a round bird "swell":

As a result, the blue and red areas we have are:

As for the yellow areas, they also arise for standard pipes, but also arise in the case of oblique obstacles directed from the bottom up (with their curved blue triangles and in general):

Well, actually, a video with bots:
In the video you can see how 50 birds quite successfully reach 1000, how all kinds of colored areas look from the point of view of the bot, and how the game would look if 1000 birds flew at the same time. In unpainted areas, bots behave randomly: each of them has its own fixed probability of deciding to jump at any given time. You can notice that from the point of view of the bot, the colored areas are slightly larger than from the point of view of mathematics. The fact is that the bot has the ability to make decisions only 60 times per second, and the physical model is also updated discretely.
Conclusion
So, it turns out that even in such a simple game like Flappy Bird there is where to develop a mathematical theory. And in fact, the most interesting from this moment is just beginning. Next, the question arises of how to deal with obstacles of arbitrary shape - here you have to introduce concepts such as a purple shadow, a burgundy border, a right-linearly connected region, a right-linearly connected closure, etc. It is also interesting what kind of reaction a person should have (that is, what a permissible time error for tapes should be) so that he can play endlessly. Incidentally, this is an extremely non-trivial question, the rigorous answer to which we still do not know.
