Animated graphs in R (and a little about bifurcation, chaos and attractors)
 Once for a presentation, I needed animated graphics. With the graphs, in fact, there were no problems, and for their animation I had to use another package
Once for a presentation, I needed animated graphics. With the graphs, in fact, there were no problems, and for their animation I had to use another package animationthat can be installed from CRAN.install.packages("animation")
library(animation)
It is worth noting that
animationin the process of image processing uses the ImageMagick software package , so it is advisable to install it in advance. Under Windows, I did not test the performance of this solution. To create an animated graph, in general, we need only one function of this kind:
saveGIF({
# Какой-то код, генерирующий последовательность графиков
}, movie.name=..., interval=..., ani.width=..., ani.height=...)
It so happened that at that time I was taking a very informative course Introduction to Dynamical Systems and Chaos , and I was wondering how they move from relatively simple mathematical objects to very bizarre images. Take at least a logistic mapping of this kind:

This iterative function can be interpreted as the dependence of the population size on its size in the previous period of time and on a parameter
rthat is usually called the reproduction rate. Actually, the function itself is rather dull and has a very banal schedule. Interesting things manifest themselves if one considers its bifurcation diagram : by changing the parameter r, one can observe the “dynamics” of fixed points of the equation . We write the logistic mapping in R as such a function:logistic.map <- function(r, x0, n, m){
x <- rep(x0, n)
for(i in 1:(n-1)) {
x[i+1] <- r * x[i] * (1 - x[i])
}
return(x[(n-m):n])
}
We set some interesting points and initial parameters for displaying and construct a bifurcation diagram, changing the image scale along the way:
Hidden text
nrows <- 6
r.len <- 1500;
# Points of interest on the plot
R <- matrix(c(
seq(2.4, 4, length.out=r.len),
seq(3.442420, 3.639398, length.out=r.len),
seq(3.562297, 3.572910, length.out=r.len),
seq(3.569792, 3.570244, length.out=r.len),
seq(3.570005, 3.571369, length.out=r.len),
seq(3.631992, 3.633301, length.out=r.len)
), nrow=nrows, byrow=T)
X <- matrix(c(
0, 1,
0.8567335, 0.9140401,
0.8887529, 0.8936790,
0.8920580, 0.8925577,
0.8911242, 0.8927333,
0.9066966, 0.9083943
), nrow=nrows, byrow=T)
x0 <- 0.5
n <- 200
m <- 170
saveGIF({
for (i in 1:nrows){
r <- R[i,]
x <- as.vector(sapply(r, logistic.map, x0, n, m))
r <- sort(rep(r, (m+1)))
del_idx <- unlist(sapply(1:length(x), function(j) if (x[j] < X[i, 1] | x[j] > X[i, 2]) j))
if (length(del_idx > 0)){
x <- x[-del_idx]
r <- r[-del_idx]
}
plot(x ~ r, col="gray66", pch=".", main="Bifurcation Diagram for the Logistic Map")
}
}, movie.name = "bifur.gif", interval=2.4, ani.width=600, ani.height=500)
As a result, we get approximately the following picture:

You can notice that the number of fixed points of the equation doubles, thus forming a cascade of bifurcations and showing a fractal structure. Here it is still appropriate to recall such a phenomenon as universality. We consider two equations:


The first equation determines the distance from one bifurcation point to the next in units
r. The second one shows how branch n is longer than branch n + 1. So, it turns out that
The number 4.669201 ... is called the universal Feigenbaum constant , which precisely characterizes the rate of transition of dynamic systems from order to deterministic chaos.
Another interesting and no less famous object is the Lorenz attractor . On Habré even a separate article is devoted to him . To describe the movement of air currents, Edward Lorenz used a system of three ordinary differential equations, now known as the Lorentz equations:
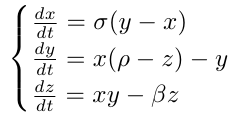
We will not go out and solve this system numerically - using the Euler method :
lorenz.solution <- function(sigma=10, r=28, beta=8/3, x=0.01, y=0.01, z=0.01, dt=0.001, n=30000){
sol <- array(0, dim=c(n,3))
t <- 0
for(i in 1:n){
x0 <- x; y0 <- y; z0 <- z
x <- x0 + (y0 - x0) * sigma * dt
y <- y0 + ((r - z0) * x0 - y0) * dt
z <- z0 + (x0 * y0 - beta * z0) * dt
t <- t + dt
sol[i,] <- c(x, y, z)
}
return(sol)
}
The system solution for the default parameters looks like this:

By changing the parameter r, we can obtain a series of images that show how the system evolves from the initial conditions and a fixed point to, in fact, a strange attractor .
library(scatterplot3d)
saveGIF({
for (r in 2:34){
sol <- lorenz.solution(r=r)
s3d<-scatterplot3d(sol[,1], sol[,2], sol[,3], color="gray66", angle=15, box=F, grid=F, axis=F, pch=".", main=paste0("Lorenz Attractor with rho=", r))
}
}, movie.name = "lorenz.gif", interval=.3, ani.width=500, ani.height=500)

The Lorenz attractor is not one of a kind. For example, the Chen attractor is described as follows:
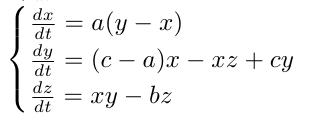
Hidden text

chen.solution <- function(a=40, c=28, b=3, x=-0.1, y=0.5, z=-0.6, dt=0.001, n=30000){
sol <- array(0, dim=c(n,3))
t <- 0
for(i in 1:n){
x0 <- x; y0 <- y; z0 <- z
x <- x0 + (y0 - x0) * a * dt
y <- y0 + ((c - a) * x0 - x0 * z0 + c * y0) * dt
z <- z0 + (x0 * y0 - b * z0) * dt
t <- t + dt
sol[i,] <- c(x, y, z)
}
return(sol)
}
saveGIF({
for (a in 32:45){
sol <- chen.solution(a=a)
s3d<-scatterplot3d(sol[,1], sol[,2], sol[,3], color="gray66", angle=15, box=F, grid=F, axis=F, pch=".", main=paste0("Chen Attractor with a=", a))
}
}, movie.name = "chen.gif", interval=.25, ani.width=500, ani.height=500)

The orbits along which the movement occurs are “pulled together” to the attractor; this movement is chaotic and sensitive to initial conditions, at the same time it is stable globally. David Feldman, who teaches the Introduction to Dynamical Systems and Chaos course, says that while in chaotic systems it is difficult to predict the state of a particular point, the statistical parameters of such systems are well defined. Thus, it can be argued about the statistical predictability of the system. For example, the weather at a particular moment, strictly speaking, is unpredictable, but the climate has quite certain parameters. And there is no contradiction.
