Modeling a Poisson process

Introduction

One of the most important processes observed in nature is the Poisson point process. Therefore, it is important to understand how such processes can be modeled. Modeling methods differ depending on the type of Poisson point process, i.e., the space in which the process takes place and the homogeneity or heterogeneity of the process. We will not be interested in the development of a Poisson point flow or with important applications in various fields. To make this material interesting, the reader is urged to read the relevant sections in Feller (1965) and Sinlar (1975) for the basic theory and some sections in Trivedi (1982) for applications in IT.

In the first step, we define the Poisson process on [0; + ∞). The process is completely determined by a family of random events that occur at certain random times 0 <T1 <T2 <... These events can relate to a lot of things, such as a bank robbery, the birth of five twins, and a Montreal taxi accident. If N (t1, t2) is the number of events that occurred during the time interval (t1, t2), then the following two conditions are often fulfilled:

• For the disjoint intervals (t1, t2) and (t3, t4), the random variables N (t1, t2) and N (t3, t4) are independent
• N (t1, t2) is distributed as well as N (0, t2-t1), i.e., the distribution of the number of events over a certain time depends only on the length of this interval.

It is an amazing fact that these two conditions entail that all random variables N (t1, t2) are distributed according to the Poisson law and that there exists a non-negative constant λ such that N (t, t + a) is distributed according to the law Po (λa ) for any non-negative t and a> 0. See, for example, Feller (1965). Thus, the Poisson distribution occurs quite naturally.

The previous concept can be generalized to R ^d . Let A be a subset of R ^d , and N be a random variable that takes only integer values. Let X ₁ , ... X _N be a set of random vectors taking a value in A. Then we say that X _i define a uniform or homogeneous Poisson process on A if

• For any finite set of pairwise disjoint subsets of the set A A _{i of} finite volume, the events N (A ₁ ), ..., N (A _{k are} independent
• For any Borel subset B of A, the distribution N (B) depends only on the volume of B

Translator's note: It would be better to use the word "measure", but for those who are not interested in mathematics, then they would have to explain a dozen pages, or even more.

Again, these assumptions entail that all N (B) are distributed according to the law P (λVol (B)) for some non-negative λ, which we call the intensity, or the intensity parameter of a homogeneous Poisson process on A. Examples of such processes in multidimensional Euclidean space include bacteria on a petri dish and the Houston killings.

Modeling homogeneous Poisson processes

If we need to simulate a uniform Poisson process on a set A belonging to R _d , then we need to generate a number of random vectors X _i from A. By Theorem 1.1, this can be done as follows:

Сгенерировать пуассоновскую случайную величину N с параметром λVol(A)
Сгенерировать независимые случайные вектора X1,..,XN, равномерно распределённые на А
RETURN Х1,...,ХN

To generate the value N, it is useless to use an algorithm with average complexity O ( 1), since at the end of the algorithm, we spend at least Ω (n) operations. Therefore, if this algorithm is used, it is highly recommended to generate a Poisson random variable with a very simple algorithm (with average time growing as O (λ)). For certain sets A, other methods can be used that do not require the explicit generation of a Poisson random variable. There are three cases that we use to illustrate this.

1. A = [0; + ∞)
2. A - circle
3. A - rectangle

To do this, we need an interesting connection between the Poisson process and the exponential distribution.


Theorem 1.2 offers the following method for modeling a uniform Poisson process on A = [0; + ∞)

T = 0 (вспомогательная переменная для обновления "времени")
k = 0 (инициализировать счётчик событий)
REPEAT
Сгенерировать экспоненциальную случайную величину Е
k = k + 1
T = T + E/λ
T[k] = T
UNTIL Ложь (это бесконечный цикл; по желанию можно добавить критерий остановки)

This algorithm is easy to implement, since there is no need to generate Poisson random variables. For other simple sets A, there are trivial generalizations of Theorem 1.2. For example, when A = [0, t] x [0,1], where t can equal infinity, 0 <T1 <T2 <... is a uniform Poisson process with intensity λ and U1, U2, ... is a sequence of independent identically distributed uniformly on [0,1] random variables, then (T1, U1), (T2, U2), ... determine the Poisson process with intensity λ on A.

Example 1.1

A uniform Poisson process on a unit circle
If A is a circle with a unit radius, then different properties of a uniform Poisson process can be used to obtain several generation methods (which generalize to d-dimensional spheres). Let λ be the desired intensity.
First, we could simply generate a random Poisson value N with parameter λπ, and then return a sequence of N independent vectors equally distributed uniformly on the unit circle. If we apply the method of order statistics proposed by Theorem 1.2, then the Poisson random variable is obtained implicitly. For example, going to the polar coordinates (R, φ), we note that for a uniform Poisson process, R and φ are independent, and the random variable R has a density of 2r, r varies from 0 to 1, and φ is evenly distributed on [0; 2π]. Thus, we can proceed as follows: Generate a uniform Poisson process 0 <φ1 <φ2 <... <φN with the intensity parameter λ / (2π) on [0; 2π] by the exponential method and return (φ1, R1), ..., (φN, RN), where Ri are independent identically distributed random variables with a density of 2r on [0; 1], which can be generated by taking a maximum of two independent random variables uniformly distributed on [0; 1]. There is no particular reason to apply the exponential method to corners. In the same way, we could pick up the radii. Unfortunately, ordinal radii do not form a one-dimensional uniform Poisson process on [0; 1]. However, nevertheless, they form an inhomogeneous Poisson process, and the generation of such processes will be considered in the next section. ordinal radii do not form a one-dimensional uniform Poisson process on [0; 1]. However, nevertheless, they form an inhomogeneous Poisson process, and the generation of such processes will be considered in the next section. ordinal radii do not form a one-dimensional uniform Poisson process on [0; 1]. However, nevertheless, they form an inhomogeneous Poisson process, and the generation of such processes will be considered in the next section.

Inhomogeneous Poisson Processes

There are situations when events occur at “random times”, but some moments are more possible than others. This is a case of arrivals at intensive care centers, job offers at computer centers, and injury to NHL players. For these cases, a very good model is the model of the heterogeneous Poisson process, defined here for convenience at [0; + ∞). This is the most important case, since time is most often a “running variable”.
The inhomogeneous Poisson process on [0; + ∞) is determined by the non-negative definite intensity function Λ (t), which can be considered as some kind of density with the difference that its integral over [0; + ∞) is not necessarily equal to 1 (usually, it diverges ) The process is determined by the following property: for any finite collection of disjoint intervals A1, A2, ..., Ak, the number of events occurring in these intervals (N1, ..., Nk) are independent Poisson random variables with parameters

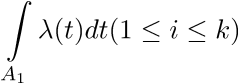
Now we will consider how such processes can be modeled. In modeling, we understand that the times when events occur, 0 <T1 <T2 <... should be given in ascending order. Much work on modeling heterogeneous Poisson processes was done by Lewis and Shedler (1979). This entire section is a revised version of their work. It is interesting to observe that the general principles of generating continuous random variables can be extended: we will see that there are analogues by the method of inversion, deviation, and composition.
The role of the distribution function will be taken by the integrated intensity function.

We begin by noting that if T _n = T, then T _{n + 1} -T _n has a distribution function

if the function Λ (t) increases unlimitedly with increasing t. This follows from the fact that in



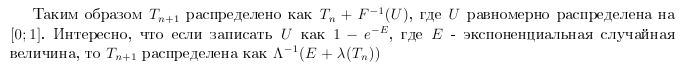
other words, we need to invert Λ. Formally, we have (see also Sinlar (1975) or Bretley, Fox and Schrage (1983)) an algorithm based on the inverse of the integral of the intensity function (inversion method)

T = 0 (вспомогательная переменная)
k = 0 (счётчик)
REPEAT
Сгенерировать экспоненциальную случайную величину E
k = k+1
T = T + InvΛ(E+Λ(T)), (InvΛ - обратная функция к Λ)
T[k] = T
UNTIL False

Example 1.2 Homogeneous Poisson Process

For the special case λ (t) = λ, Λ (t) = λt, it is easy to see that InvΛ (E + Λ (T)) = T + E / λ, as a result of which we again obtain the exponential method.

Example 1.3

To simulate the morning flow of cars before rush hour, we can sometimes take λ (t) = t, then Λ (t) = t ^ 2/2 and get the step

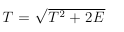
If the intensity function can be represented as a sum of intensity functions, i.e. ,

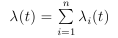0 <T _i1 <T _i2 <... T _inAre independent implementations of individual inhomogeneous Poisson processes, then the combined ordered sequence forms an implementation of an inhomogeneous Poisson process with intensity function λ (t). This applies to the composition method, but the difference now is that we need implementations of all process components. Decomposition can be used when there is a natural decomposition dictated by the analytic form λ (t). Since the main operation in the merging of processes is to take the minimum value from n processes, for large n the advantage can be provided by storing time instants in a heap of n elements.

As a result, we obtain the composition method:

Сгенерировать T[1,1],...,T[n,1] для n пуассоновских процессов и хранить эти значения вместе с индексами соответствующих процессов в таблице
T = 0 (текущее время)
k = 0
REPEAT
Найти минимальный элемент T[i,j] в таблице и удалить его
k = k + 1
T[k] = T[i,j]
Сгенерировать T[i,j+1] и вставить в таблицу
UNTIL False

The third general principle is the principle of thinning (Lewis and Shedler, 1979). Similar to what happens in the deviation method, we assume that there is a slight dominant intensity function λ (t) <= μ (t) for any t.

Then the idea is to generate a homogeneous Poisson process on the part of the positive half-plane between 0 and μ (t), then consider a homogeneous Poisson process under λ and, finally, return the x-components of the events in this process. This requires the following theorem.




Now consider the method of thinning Lewis and Shedler:

T = 0
k = 0
REPEAT
Сгенерировать Z, первое событие в неоднородном пуассоновском процессе с функцией интенсивности μ, который происходит после момента времени T. Присвоить T = Z
Сгенерировать равномерно распределённую на [0;1] случайную величину U
IF U <= λ(Z)/μ(Z)
THEN k = k + 1, X[k] = T
UNTIL False

It is argued that the sequence X _kthus, the generated one forms an inhomogeneous Poisson process with an intensity function λ. Note that we took the non-uniform process 0 <Y1 <Y2 <... with the intensity function μ and removed some points. As far as we know, (Y _i , U _i μ (Y _i ) is a homogeneous Poisson process with unit intensity on the curve if U _{i are} independent random variables identically distributed uniformly on [0; 1] by virtue of Theorem 1.3. Thus, the subsequence on curve λ defines a homogeneous Poisson process with unit intensity on this curve (part 3. of Theorem 1.3). Finally, taking the x-coordinates of only this subsequence gives us an inhomogeneous Poisson process with intensity function λ.
An inhomogeneous Poisson process with an intensity function μ is usually modeled by the inversion method.

Example 1.4 Cyclic intensity function

The following example also belongs to Lewis and Shedler (1979). Consider a function with cyclic intensity λ (t) = λ (1 + cos (t)) with an obvious choice of the dominant function μ = 2λ.

Then the simulation algorithm will take the form:

T = 0
k = 0
REPEAT
Сгенерировать экспоненциальную случайную величину E c параметром 1
T = T + E/(2λ)
Сгенерировать равномерную на [0;1] случайную величину U
IF U <= (1+cos(T))/2
THEN k = k + 1, X[k] = T
UNTIL False

There is no need to say that you can use the theorem on two policemen here to avoid calculating the cosine in most cases.

The final word on the effectiveness of the algorithm when an inhomogeneous Poisson process is modeled on the set [0, t]. The average number of events that is needed from the dominant process is equal , while the average number of returned random variables is
The ratio of the average values ​​can be considered as an objective measure of efficiency, comparable in the spirit of the deviation constant in the standard deviation method. Note that we cannot use the average value of the ratio, since in the general case it would be equal to infinity due to the positive probability that no value will return.