Solving Japanese Crosswords in Wolfram Mathematica

Japanese Crossword is a well-known puzzle whose answer is drawing. What is it and how to solve it, you can read on Wikipedia . I want to show how you can write a program that will solve the Japanese crossword in Wolfram Mathematica by enumeration.

Main ideas

The idea of ​​a brute-force solution is to create lists of all kinds of cell locations for all rows and columns. After that, using the lists obtained, find those cells whose information will be accurately known. Then weed out such locations that contradict the information found. Intuitively, if you cyclically repeat the last two procedures, you can find information about any cell. So, the task can be divided into three subtasks:

1. Compilation of all possible locations.
2. Search for filled and unfilled cells.
3. Removing conflicting locations.

Since Wolfram Mathematica is designed to work with lists, cell locations will be stored in the program as lists. We will denote information about cells as follows:

• 1 - filled cell;
• 0 - unfilled cell;
• * - a cell about which nothing is known.

For example, below are shown the equivalent list and arrangement of cells:

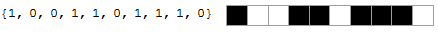
Compilation of all possible locations

Bit of theory

Consider a specific example. It is necessary to find all possible locations for such data:

One of these locations is shown above. How to sort through all possible locations?

Let's do it the next way. We assign to key (left of the figures), such groups of cells: {{1,0}, {1,1,0}, {1,1,1}}. Now create a list that will store the places where we will arrange these groups in order. In the places where we will put these groups, we will store zeros. Thus, we get a list of places {0,0,0,0,0}. Arranging the groups of cells in order by all means into the obtained places, it is easy to verify that we obtain all the required arrangements for the data from the task. If you put the groups in order in the places with numbers 1, 3, 4, you get the arrangement from the example above. Thus, it turns out that all arrangements are equivalent to combinationsfrom the number of places by the number of groups. Choosing in some way places where to put groups, we get one of the possible locations. For the data in the example, the number of locations is ten.

To the questions “Why is there no zero at the end in the last group?” And “Why are there exactly five seats?” The conscious reader must answer himself.

Implementation

It is clear that there is no special desire to write the function itself that will enumerate, because in Mathematica there is a built-in function Subsets[list, {n}]that will do this. It accepts a list of listthe set of elements and the number nas a parameter and returns a list of subsets of the set listlength n. For our example, its use for enumerating all places will look like this: Now we will write our own function, which will take a number (field length , for example data - ) and a list (key , for example data -

In := Subsets[{1,2,3,4,5}, {3}]

Out = {{1,2,3}, {1,2,4}, {1,2,5}, {1,3,4}, {1,3,5}, {1,4,5}, {2,3,4}, {2,3,5}, {2,4,5}, {3,4,5}}


len10clue{1,2,3}) as parameters and return a list of all possible locations. We will do everything sequentially. First, create a function that turns a number into a list of units. There is a built-in function for this ConstantArray[c, n]; c- this is the element with which the list is filled, and n- the length of this list. Next, we need to append zero to the end of this list. This is done using . The first parameter is a list, the second is what we will attach. We collect these two functions into one using an object such as a pure function. This can be done in two ways: either , or shorter - . Now it remains to apply this function to each element of the list that corresponds to the key. There is a very useful feature for this.

In := ConstantArray[1, 2]

Out = {1, 1}


Append[expr, elem]

In := Append[{1, 1}, 0]

Out = {1, 1, 0}


Function[arg, Append[ConstantArray[1, arg], 0]Append[ConstantArray[1, #], 0]&

Map[f, expr]. It applies a function fto each item in the list expr. She also has a shorter version: f /@ expr. It remains only to remove zero from the last group. Here the function will help . It will remove the item from the list with the index . Do not forget that the last element has an index of -1. Putting it all together looks like this: Everything is clear with the list of places, but we need a function that summarizes the elements of the list . Now the most important thing is the use of the function . Plus we need a function that returns a list and that gives the length of the list .

In := Append[ConstantArray[1, #], 0]& /@ {1, 2, 3}

Out = {{1,0}, {1,1,0}, {1,1,1,0}}


Delete[expr, {i, j}]expr{i, j}

In := Delete[{{1,0}, {1,1,0}, {1,1,1,0}}, {-1, -1}]

Out = {{1,0}, {1,1,0}, {1,1,1}}




In := groups = Delete[Append[ConstantArray[1, #], 0]& /@ clue, {-1, -1}]

Out = {{1,0}, {1,1,0}, {1,1,1}}


Total[list]list

In := positions = ConstantArray[0, len - Total[clue] + 1]

Out = {0,0,0,0,0}


SubsetsRange[n]{1, 2, ..., n}Length[list]list

In := sub = Subsets[Range[len - Total[clue] + 1], {Length[clue]}]

Out = {{1,2,3}, {1,2,4}, {1,2,5}, {1,3,4}, {1,3,5}, {1,4,5}, {2,3,4}, {2,3,5}, {2,4,5}, {3,4,5}}


We got a list of places to arrange groups of cells. Now we will deal with the arrangement. For this we need a function ReplacePart[expr, i->new], it replaces expran element with a number in the list with ian element new. But first, we get a list of replacements, so that later it’s more convenient to write the code. This will help us to make the function MapThread[f, {a₁ , a₂ , ...}, {b₁ , b₂, ...}] . The result of its implementation will be as follows: {f[a₁ , b₁ ], f[a₂ , b₂], ...} . So, we create a list of substitutions: The final of the whole undertaking is an arrangement in its place. Here we do , which removes the extra brackets: That's all, all the constellations are received. It remains to combine all this into one module for convenience and we will get the required function.

In := rep = MapThread[Function[{x, y}, x->y], {#, groups}]& /@ sub

Out = {{1->{1,0}, 2->{1,1,0}, 3->{1,1,1}}, {1->{1,0}, 2->{1,1,0}, 4->{1,1,1}}, {1->{1,0}, 2->{1,1,0}, 5->{1,1,1}}, {1->{1,0}, 3->{1,1,0}, 4->{1,1,1}}, {1->{1,0}, 3->{1,1,0}, 5->{1,1,1}}, {1->{1,0}, 4->{1,1,0}, 5->{1,1,1}}, {2->{1,0}, 3->{1,1,0}, 4->{1,1,1}}, {2->{1,0}, 3->{1,1,0}, 5->{1,1,1}}, {2->{1,0}, 4->{1,1,0}, 5->{1,1,1}}, {3->{1,0}, 4->{1,1,0}, 5->{1,1,1}}}


Flatten[list]

In := all = Flatten[ReplacePart[positions, #]]& /@ rep

Out = {{1,0,1,1,0,1,1,1,0,0}, {1,0,1,1,0,0,1,1,1,0}, {1,0,1,1,0,0,0,1,1,1}, {1,0,0,1,1,0,1,1,1,0}, {1,0,0,1,1,0,0,1,1,1}, {1,0,0,0,1,1,0,1,1,1}, {0,1,0,1,1,0,1,1,1,0}, {0,1,0,1,1,0,0,1,1,1}, {0,1,0,0,1,1,0,1,1,1}, {0,0,1,0,1,1,0,1,1,1}}




allPositions[len_, clue_] :=

Module[{groups, positions, sub, rep, all},

groups = Delete[Append[ConstantArray[1, #], 0]& /@ clue, {-1, -1}];

positions = ConstantArray[0, len - Total[clue] + 1];

sub = Subsets[Range[len - Total[clue] + 1], {Length[clue]}];

rep = MapThread[Function[{x, y}, x->y], {#, groups}]& /@ sub;

all = Flatten[ReplacePart[positions, #]]& /@ rep;

Return[all];]


Search for filled and unfilled cells

Now among all this good that we get using our function, we need to extract information about the cells. Suppose we have some list of locations. If there is a place where in all locations there is 1 or 0, then this gives us the right to assert that at this position there will always be a filled or, respectively, unfilled cell. In my opinion, the simplest implementation of the function that will do this is as follows: all locations are summed element by element, and either numbers equal to the number of all locations or zeros are searched in the resulting list. In the first case, these numbers change to units, and in the second, the zeros remain in their places. All other elements are replaced with asterisks. To implement, use the function ReplaceAll[list, rule]. She will replace the listlistitems in accordance with the rules rule. Construction x_ /; x!=0means "an element xsuch that x ≠ 0."

findInformation[list_] := ReplaceAll[Total[list], {x_ /; x!=0 && x!=Length[list] -> "*", x_ /; x==Length[list] -> 1}]

For our example, the work of the function looks like this: The eighth cell in all locations will be shaded, so it will be shaded in the entire grid. Nothing can be said about the remaining cells.

In := findInformation[allPositions[len, clue]]

Out = {*,*,*,*,*,*,*,1,*,*}


Removing conflicting locations

The information obtained can be used to filter out locations that contradict it. The function DeleteCases[expr, pattern]will be our filter - it removes from the expr list all elements that do not match the pattern pattern. A function Except[c]that selects everything except its parameter will also be used . Returning to the example, suppose we got to the location of the cells must meet the following template: . Running our function, we get: It turned out that out of ten locations, only two satisfy the pattern.

deleteFromList[list_, test_] := DeleteCases[list, Except[ReplaceAll[test, "*"->_]]]


{*,*,0,0,*,1,0,*,*,*}

In := deleteFromList[allPositions[len, clue], {"*","*",0,0,"*",1,0,"*","*","*"}]

Out = {{1,0,0,0,1,1,0,1,1,1}, {0,1,0,0,1,1,0,1,1,1}}


Putting it all together. Final stage

We created all the necessary functions to solve the crossword puzzle step by step. Now it’s important to collect everything beautifully in order to get a solution. As an example, I use a crossword puzzle, taken from the Kiev magazine of Japanese crosswords "Relax". Its author is A. Leuta.

A crossword puzzle is set in the program in the form of a list of keys for rows and columns. You do not need to enter grid sizes, because you can define them in such a way: In the program, the picture will be stored as a list of lists or an ordinary matrix. Before the decision, we do not have information at all, so each element of it will be an asterisk. Now, the most cumbersome part of the crossword puzzle solution is filling out lists of all kinds of locations. Here you need to wait a bit.

rows = {{1}, {2}, {4}, {3,1}, {4,1}, {12}, {9}, {4,1}, {1,1,1,1,1}, {1,1,1,1}, {1,3,1}, {2,1,1}, {9,1}, {4,5,1}, {3,4,1}, {3,5,3}, {3,1,5}, {5,1,2}, {7,3}, {4,10}, {4,3,3}, {4,2,3}, {5,2,2}, {5,3,2}, {4,1,1,2}, {3,2,2}, {2,2}, {7}, {10}, {2,6}};

cols = {{3}, {6}, {8}, {13}, {1,12,1}, {2,7,2,1}, {5,2,7,4}, {5,3,12}, {8,2,3,1,1,2}, {8,2,1,3}, {2,3,4,1,4}, {2,2,1,1,5,3,5}, {4,6,7,2}, {2,3,3,8,2}, {1,2,2,2}, {1,4,1}, {2}, {2}, {9}, {1}};




rowlength = Length[cols]

collength = Length[rows]




pic = ConstantArray["*", {collength, rowlength}];




rowpos = allPositions[rowlength, #]& /@ rows;

colpos = allPositions[collength, #]& /@ cols;


When all the locations are full, you can proceed with the decision. The idea is this: a search is performed on all rows of filled cells and these cells are recorded in the main grid. Then, those that contradict the information received are removed from the column layouts and the columns are searched, and so on. The search will go on until there is at least one asterisk in the grid; I think that the work of the cycle Whiledoes not need to be explained. MemberQin the above code returns Trueif there is an asterisk in the grid and Falsein the opposite case. Transpose ( Transpose) is also used so that you can work equally with both rows and columns. There is a built-in function for drawing output.ArrayPlot, which paints the cell black if it is 1 and white if 0 (the asterisk is browned by default). In order to see how the picture dynamically changes in the process of solving, it is used Dynamic. The result is this picture:

Dynamic[ArrayPlot[pic, Mesh->True]]

While[MemberQ[pic, "*", 2],

pic = findInformation /@ rowpos;

colpos = MapThread[deleteFromList, {colpos, Transpose[pic]}];

pic = Transpose[findInformation /@ colpos];

rowpos = MapThread[deleteFromList, {rowpos, pic}];]




Perhaps someone noticed that the solution is very suboptimal. Yes, it is, but optimality is not the point. The purpose of the article is to show that Wolfram Mathematica can solve such a problem conveniently and quickly. But if we are already talking about optimality, then there are many ways to optimize the algorithm for this task, for example, filtering and searching for information only in those columns and rows whose cell information was added in the previous step, in this version of the program, the search is performed in all columns and lines.