When it is not necessary to use algorithms from STL
- Transfer
I struggled with the temptation to call an article like “The terrifying inefficiency of STL algorithms” - well, you know, just for the sake of training in the skill of creating flashy headlines. But still I decided to remain within the framework of decency - it is better to get comments from the readers on the content of the article than resentment about its loud title.
In this place, I will assume that you know a little C ++ and STL, and also take care of the algorithms used in your code, their complexity and compliance with the tasks set.
One of the well-known tips that you can hear from the modern C ++ developer community will not come up with bicycles, but use algorithms from the standard library. This is good advice. These algorithms are safe, fast, tested over the years. I also often give advice to apply them.
Every time you want to write a regular for - you should first remember whether there is something in the STL (or in boost) that already solves this problem in one line. If there is - it is often better to use it However, we, in this case as well, should understand that the algorithm lies behind the call to the standard function, what are its characteristics and limitations.
Usually, if our problem exactly matches the description of the algorithm from the STL, it would be a good idea to take and apply it in the forehead. The only trouble is that the data is not always stored in the form in which the algorithm implemented in the standard library wants to receive it. Then we may have an idea to first convert the data, and then still apply the same algorithm. Well, you know, like in that joke about the mathematician “Put out the fire from the kettle. The task is reduced to the previous one. ”
Imagine that we are trying to write a tool for C ++ programmers who will find in the code all lambdas with capturing all variables by default ([=] and [&]) and display tips on converting them to lambdas with a specific list of variables to be captured. Something like that:
In the course of parsing a file with a code, we will have to store a collection of variables somewhere in the current and surrounding scope, and when a lambda is found to capture all the variables, compare these two collections and give advice on how to transform it.
One set with variables of the parent scope, and another with variables inside the lambda. To form an advice, a developer only needs to find their intersection. And this is the case when the description of the algorithm from STL is just perfect for the task: std :: set_intersection accepts two sets and returns their intersection. The algorithm is beautiful in its simplicity. It takes two sorted collections and runs through them in parallel:
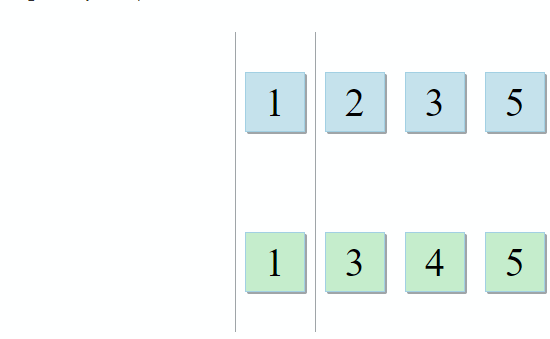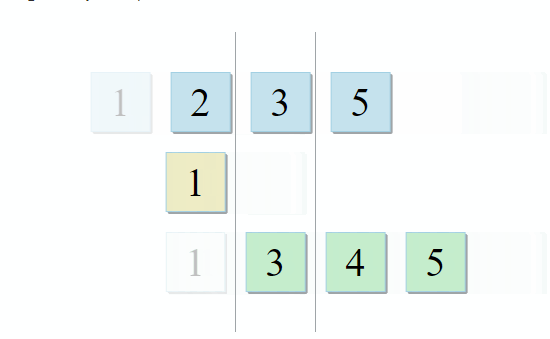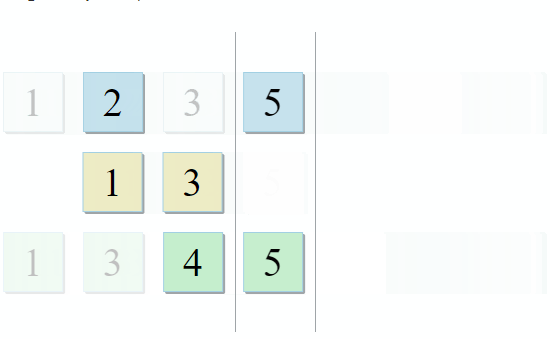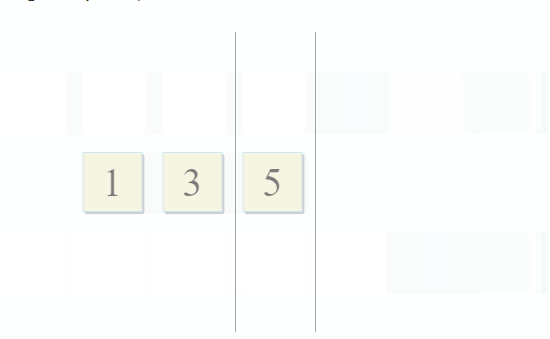
With each step of the algorithm, we move along the first, second, or both collections, which means the complexity of this algorithm will be linear - O (m + n), where n and m are the sizes of the collections.
Simple and effective. But this is only as long as the input collections are sorted.
The problem is that, in general, collections are not sorted. In our particular case, it is convenient to store variables in some kind of stack-like data structure, adding variables to the next level of the stack upon entering the nested scope and removing them from the stack when exiting this scope.
This means that the variables will not be sorted by name, and we cannot directly use std :: set_intersection on their collections. Since std :: set_intersection requires exactly sorted collections at the input, a thought may arise (and I often saw this approach in real projects) sort the collections before calling the library function.
Sorting in this case will kill the whole idea of using the stack to store variables according to their scopes, but still it is possible:
What is the complexity of the resulting algorithm? Something of type O (n log n + m log m + n + m) is a quasilinear complexity.
Can we not use sorting? We can, why not. We will simply search for each element from the first collection to the second, by a linear search. We obtain the complexity of O (n * m). And I also saw this approach in real projects quite often.
Instead of the options "sort everything" and "not sort anything" we can try to find Zen and go the third way - sort only one of the collections. If one of the collections is sorted, and the second is not, then we will be able to iterate over the elements of the unsorted collection one by one and search for them in a sorted binary search.
The complexity of this algorithm will be O (n log n) for sorting the first collection and O (m log n) for searching and checking. In sum, we obtain the complexity O ((n + m) log n).
If we decide to sort another from the collections, then we get the complexity O ((n + m) log m). As you understand, it will be logical to sort a smaller collection here to obtain the final complexity O ((m + n) log (min (m, n)).
The implementation will look like this:
In our example with lambda functions and variable capture, the collection that we will sort will usually be a collection of variables used in the lambda function code, since they are likely to be smaller than the variables in the lambda surrounding scope.
And the last option considered in this article is to use hashing for a smaller collection instead of sorting it. This will give us the opportunity to search for it in O (1), although the construction of the hash itself, of course, will take some time (from O (n) to O (n * n), which can be a problem):
The hashing approach will be an absolute winner in the case when our task is to consistently compare a small set A with a set of other (large) sets B₁, B₂, B .... In this case, we need to build a hash for A only once, and its instant search can be used to compare with the elements of all the considered sets B.
It is always useful to confirm the theory with practice (especially in cases like the latter, when it is not clear whether the initial costs of hashing will be paid back by a gain in performance on the search).
In my tests, the first option (with sorting of both collections) always showed the worst results. Sorting only one smaller collection worked a little better on collections of the same size, but not too much. But the second and third algorithms showed a very significant increase in productivity (about 6 times) in cases where one of the collections was 1000 times larger than the other.
In this place, I will assume that you know a little C ++ and STL, and also take care of the algorithms used in your code, their complexity and compliance with the tasks set.
Algorithms
One of the well-known tips that you can hear from the modern C ++ developer community will not come up with bicycles, but use algorithms from the standard library. This is good advice. These algorithms are safe, fast, tested over the years. I also often give advice to apply them.
Every time you want to write a regular for - you should first remember whether there is something in the STL (or in boost) that already solves this problem in one line. If there is - it is often better to use it However, we, in this case as well, should understand that the algorithm lies behind the call to the standard function, what are its characteristics and limitations.
Usually, if our problem exactly matches the description of the algorithm from the STL, it would be a good idea to take and apply it in the forehead. The only trouble is that the data is not always stored in the form in which the algorithm implemented in the standard library wants to receive it. Then we may have an idea to first convert the data, and then still apply the same algorithm. Well, you know, like in that joke about the mathematician “Put out the fire from the kettle. The task is reduced to the previous one. ”
Intersection of many
Imagine that we are trying to write a tool for C ++ programmers who will find in the code all lambdas with capturing all variables by default ([=] and [&]) and display tips on converting them to lambdas with a specific list of variables to be captured. Something like that:
std::partition(begin(elements), end(elements),
[=] (auto element) {
//^~~ - захватывать всё подряд не хорошо, замените на [threshold]return element > threshold;
});In the course of parsing a file with a code, we will have to store a collection of variables somewhere in the current and surrounding scope, and when a lambda is found to capture all the variables, compare these two collections and give advice on how to transform it.
One set with variables of the parent scope, and another with variables inside the lambda. To form an advice, a developer only needs to find their intersection. And this is the case when the description of the algorithm from STL is just perfect for the task: std :: set_intersection accepts two sets and returns their intersection. The algorithm is beautiful in its simplicity. It takes two sorted collections and runs through them in parallel:
- If the current item in the first collection is identical to the current item in the second, add it to the result and proceed to the next items in both collections.
- If the current item in the first collection is less than the current item in the second collection, go to the next item in the first collection.
- If the current item in the first collection is greater than the current item in the second collection, go to the next item in the second collection.

With each step of the algorithm, we move along the first, second, or both collections, which means the complexity of this algorithm will be linear - O (m + n), where n and m are the sizes of the collections.
Simple and effective. But this is only as long as the input collections are sorted.
Sorting
The problem is that, in general, collections are not sorted. In our particular case, it is convenient to store variables in some kind of stack-like data structure, adding variables to the next level of the stack upon entering the nested scope and removing them from the stack when exiting this scope.
This means that the variables will not be sorted by name, and we cannot directly use std :: set_intersection on their collections. Since std :: set_intersection requires exactly sorted collections at the input, a thought may arise (and I often saw this approach in real projects) sort the collections before calling the library function.
Sorting in this case will kill the whole idea of using the stack to store variables according to their scopes, but still it is possible:
template <typename InputIt1, typename InputIt2, typename OutputIt>
autounordered_intersection_1(InputIt1 first1, InputIt1 last1,
InputIt2 first2, InputIt2 last2,
OutputIt dest){
std::sort(first1, last1);
std::sort(first2, last2);
returnstd::set_intersection(first1, last1, first2, last2, dest);
}What is the complexity of the resulting algorithm? Something of type O (n log n + m log m + n + m) is a quasilinear complexity.
Less sorting
Can we not use sorting? We can, why not. We will simply search for each element from the first collection to the second, by a linear search. We obtain the complexity of O (n * m). And I also saw this approach in real projects quite often.
Instead of the options "sort everything" and "not sort anything" we can try to find Zen and go the third way - sort only one of the collections. If one of the collections is sorted, and the second is not, then we will be able to iterate over the elements of the unsorted collection one by one and search for them in a sorted binary search.
The complexity of this algorithm will be O (n log n) for sorting the first collection and O (m log n) for searching and checking. In sum, we obtain the complexity O ((n + m) log n).
If we decide to sort another from the collections, then we get the complexity O ((n + m) log m). As you understand, it will be logical to sort a smaller collection here to obtain the final complexity O ((m + n) log (min (m, n)).
The implementation will look like this:
template <typename InputIt1, typename InputIt2, typename OutputIt>
autounordered_intersection_2(InputIt1 first1, InputIt1 last1,
InputIt2 first2, InputIt2 last2,
OutputIt dest){
constauto size1 = std::distance(first1, last1);
constauto size2 = std::distance(first2, last2);
if (size1 > size2) {
unordered_intersection_2(first2, last2, first1, last1, dest);
return;
}
std::sort(first1, last1);
returnstd::copy_if(first2, last2, dest,
[&] (auto&& value) {
returnstd::binary_search(first1, last1, FWD(value));
});
}In our example with lambda functions and variable capture, the collection that we will sort will usually be a collection of variables used in the lambda function code, since they are likely to be smaller than the variables in the lambda surrounding scope.
Hashing
And the last option considered in this article is to use hashing for a smaller collection instead of sorting it. This will give us the opportunity to search for it in O (1), although the construction of the hash itself, of course, will take some time (from O (n) to O (n * n), which can be a problem):
template <typename InputIt1, typename InputIt2, typename OutputIt>
voidunordered_intersection_3(InputIt1 first1, InputIt1 last1,
InputIt2 first2, InputIt2 last2,
OutputIt dest){
constauto size1 = std::distance(first1, last1);
constauto size2 = std::distance(first2, last2);
if (size1 > size2) {
unordered_intersection_3(first2, last2, first1, last1, dest);
return;
}
std::unordered_set<int> test_set(first1, last1);
returnstd::copy_if(first2, last2, dest,
[&] (auto&& value) {
return test_set.count(FWD(value));
});
}The hashing approach will be an absolute winner in the case when our task is to consistently compare a small set A with a set of other (large) sets B₁, B₂, B .... In this case, we need to build a hash for A only once, and its instant search can be used to compare with the elements of all the considered sets B.
Performance test
It is always useful to confirm the theory with practice (especially in cases like the latter, when it is not clear whether the initial costs of hashing will be paid back by a gain in performance on the search).
In my tests, the first option (with sorting of both collections) always showed the worst results. Sorting only one smaller collection worked a little better on collections of the same size, but not too much. But the second and third algorithms showed a very significant increase in productivity (about 6 times) in cases where one of the collections was 1000 times larger than the other.
