Maze Path Algorithm
Good day, dear community.
One fine day, walking the expanses of the Internet, a maze was found. It became interesting to know its passage and taking a walk on the network, I still could not find a working software implementation, the solution to the maze.
The working day was boring, the mood was excellent. A goal, means and desire are available. The conclusion is obvious, we will pass.
For a convenient solution, you must have the existing image of the maze, lead to the type of two-dimensional array. Each element of which can take one of 3 values:
For starters, you need to re-save the image as a monochrome bmp, in order to have 2 colors white or black. If you look closely at the maze, then it has a wall 2 pixels thick and a road 4 pixels thick. It would be ideal to make the wall and road thickness 1 pixel. To do this, it is necessary to rebuild the image, divide the image into 3, that is, remove every 2nd and 3rd, row and column of pixels from the picture (this will not affect the correctness and patency of the maze).
1. We use the image scanning function.
2. Rebuild the image:
3. Generate the rebuilt image.
And so, we have an image of the labyrinth of the desired type, now the most interesting is the search for all the options for passing the labyrinth. What do we have? An array with the recorded values WALL - wall and BLANK - road.
There was one unsuccessful attempt to find the passage of the maze using the wave algorithm. Why unsuccessful, in all attempts, this algorithm led to a "Stack Overflow" error. I am 100% sure that using it, you can find the passage, but there was a fuse to come up with something more interesting.
The idea did not come immediately, there were several realizations of the passage, which worked for about 3 minutes in time, after which the inspiration came: “what if you look not for the paths, but for paths that do not lead to the maze and mark them as dead ends”.
The algorithm is as follows:
Perform a recursive function on all points of the labyrinth's roads:
1. If we stand on the road and around us there are 3 walls, mark the place where we stand as a dead end, otherwise we exit the function;
2. We pass to the place which is not a wall from point No. 1, and we repeat point No. 1;
Software implementation:
I got a “complete” working algorithm that can be used to find all the maze walks. The latest in speed exceeded all expectations. I hope my little work will benefit someone or encourage new thoughts.
To find the shortest path, it is planned to apply the wave algorithm to the found maze walks. It would be interesting to hear what other algorithms can be used to quickly find a path in a large maze?
Background
One fine day, walking the expanses of the Internet, a maze was found. It became interesting to know its passage and taking a walk on the network, I still could not find a working software implementation, the solution to the maze.
That's actually it:

The working day was boring, the mood was excellent. A goal, means and desire are available. The conclusion is obvious, we will pass.
History
For a convenient solution, you must have the existing image of the maze, lead to the type of two-dimensional array. Each element of which can take one of 3 values:
const
WALL=-1;
BLANK=-2;
DEADBLOCK=-3;
First, I want to show the functions for scanning the image of the labyrinth, followed by writing data to the array, and the function of generating a new image, based on data from the array:
Image Scan:
Image Generation:
...
var
N:integer=600;
LABIRINT:array[0..600,0..600] of integer;
...
var bit:TBitmap;
i,j:integer;
begin
bit:=TBitmap.Create;
If OpenDialog1.Execute then
begin
bit.LoadFromFile(OpenDialog1.FileName);
for i:=0 to N do
for j:=0 to N do
if bit.Canvas.Pixels[j,i]=clWhite then
LABIRINT[j,i]:=BLANK else LABIRINT[j,i]:=WALL;
bit.Free;
...
end;
end;
...
Image Generation:
...
var
N:integer=600;
LABIRINT:array[0..600,0..600] of integer;
...
procedure genBitmap;
var bit:TBitmap;
i,j:Integer;
begin
bit:=TBitmap.Create;
bit.Width:=N+1;
bit.Height:=N+1;
for i:=0 to N do
for j:=0 to N do
begin
if LABIRINT[i,j]=BLANK then bit.Canvas.Pixels[i,j]:=clWhite //
else
if LABIRINT[i,j]=WALL then bit.Canvas.Pixels[i,j]:=clBlack
else bit.Canvas.Pixels[i,j]:=clRed;
end;
bit.SaveToFile('tmp.bmp');
bit.Free;
end;
...
For starters, you need to re-save the image as a monochrome bmp, in order to have 2 colors white or black. If you look closely at the maze, then it has a wall 2 pixels thick and a road 4 pixels thick. It would be ideal to make the wall and road thickness 1 pixel. To do this, it is necessary to rebuild the image, divide the image into 3, that is, remove every 2nd and 3rd, row and column of pixels from the picture (this will not affect the correctness and patency of the maze).
Prepared Figure: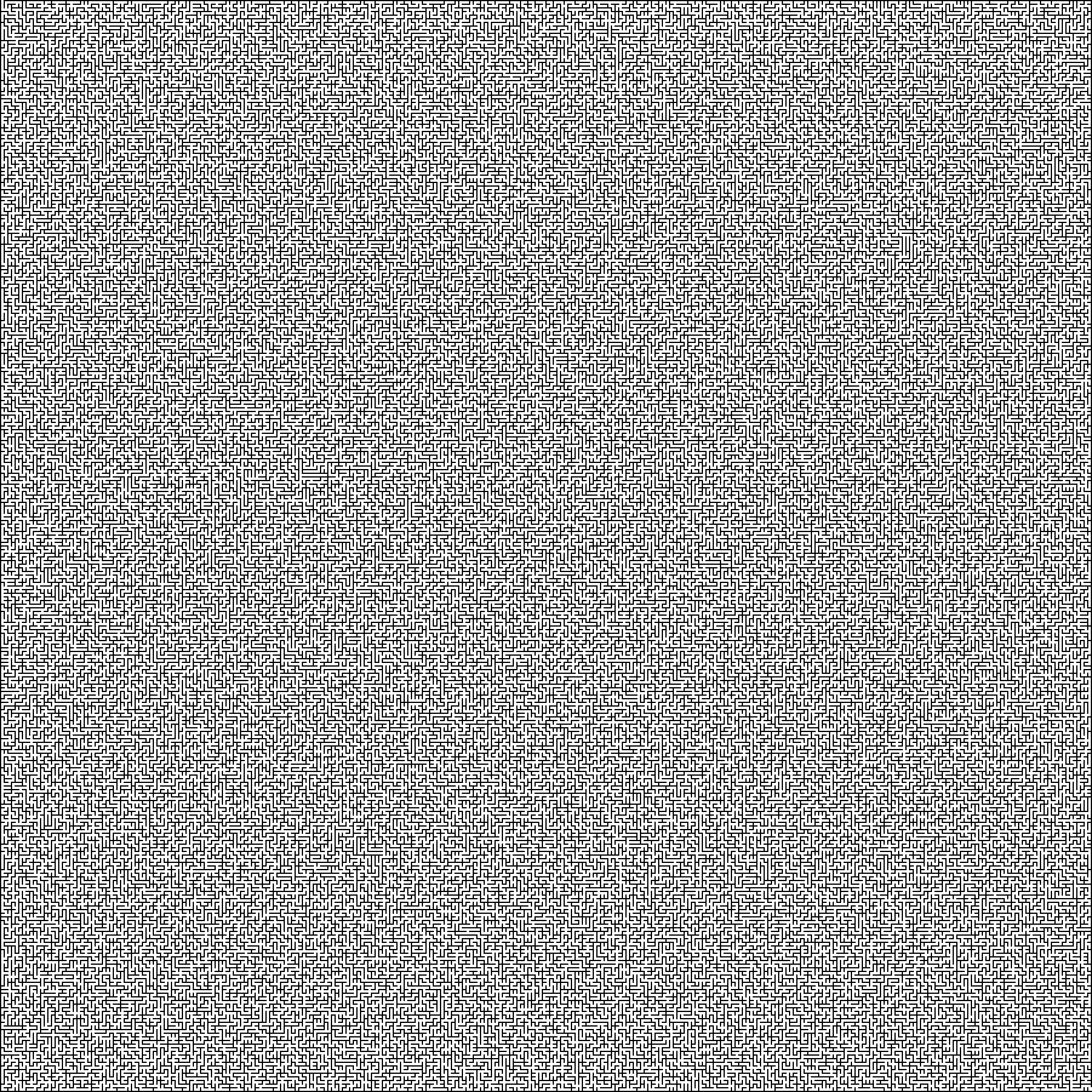
Image width and height: 1802 pixels.
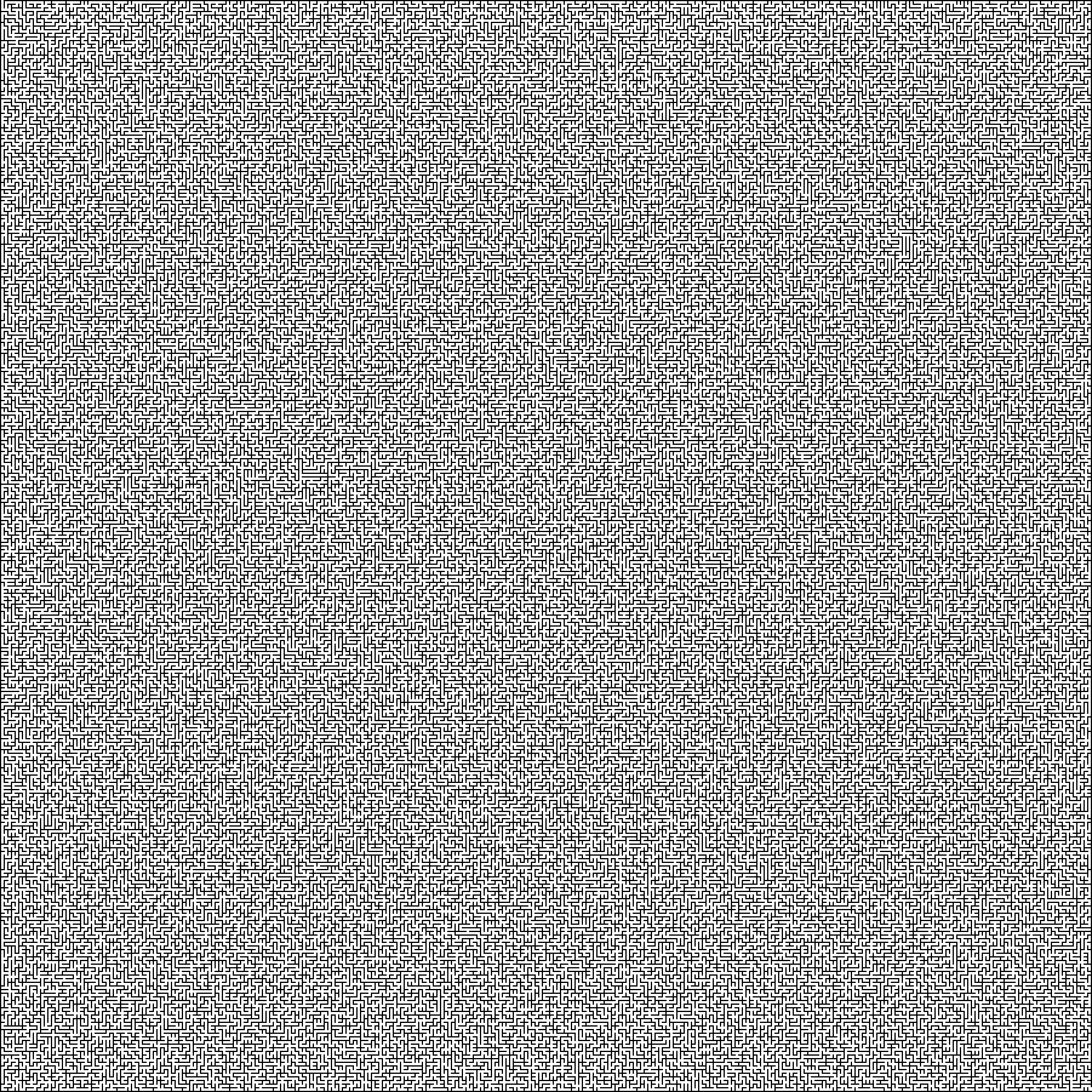
Image width and height: 1802 pixels.
1. We use the image scanning function.
2. Rebuild the image:
...
var
N:integer=1801;
LABIRINT:array[0..1801,0..1801] of integer;
...
procedure rebuildArr2;
var i,j:integer;
begin
for i:=0 to ((N div 3) ) do
for j:=0 to ((N div 3) ) do
LABIRINT[i,j]:=LABIRINT[i*3,j*3];
N:=N div 3;
end;
...
3. Generate the rebuilt image.
The result of the procedure:
Image width and height: 601 pixels.

Image width and height: 601 pixels.
And so, we have an image of the labyrinth of the desired type, now the most interesting is the search for all the options for passing the labyrinth. What do we have? An array with the recorded values WALL - wall and BLANK - road.
There was one unsuccessful attempt to find the passage of the maze using the wave algorithm. Why unsuccessful, in all attempts, this algorithm led to a "Stack Overflow" error. I am 100% sure that using it, you can find the passage, but there was a fuse to come up with something more interesting.
The idea did not come immediately, there were several realizations of the passage, which worked for about 3 minutes in time, after which the inspiration came: “what if you look not for the paths, but for paths that do not lead to the maze and mark them as dead ends”.
The algorithm is as follows:
Perform a recursive function on all points of the labyrinth's roads:
1. If we stand on the road and around us there are 3 walls, mark the place where we stand as a dead end, otherwise we exit the function;
2. We pass to the place which is not a wall from point No. 1, and we repeat point No. 1;
Software implementation:
...
var
N:integer=600;
LABIRINT:array[0..600,0..600] of integer;
...
procedure setBlankAsDeadblockRec(x,y:integer);
var k:integer;
begin
k:=0;
if LABIRINT[x,y]=blank then
begin
if LABIRINT[x-1,y]<>BLANK then k:=k+1;
if LABIRINT[x,y-1]<>BLANK then k:=k+1;
if LABIRINT[x+1,y]<>BLANK then k:=k+1;
if LABIRINT[x,y+1]<>BLANK then k:=k+1;
if k=4 then LABIRINT[x,y]:=DEADBLOCK;
if k=3 then
begin
LABIRINT[x,y]:=DEADBLOCK;
if LABIRINT[x-1,y]=BLANK then setBlankAsDeadblockRec(x-1,y);
if LABIRINT[x,y-1]=BLANK then setBlankAsDeadblockRec(x,y-1);
if LABIRINT[x+1,y]=BLANK then setBlankAsDeadblockRec(x+1,y);
if LABIRINT[x,y+1]=BLANK then setBlankAsDeadblockRec(x,y+1);
end;
end;
end;
procedure setDeadblock;
var i,j:integer;
begin
for i:=1 to N-1 do
for j:=1 to N-1 do
setBlankAsDeadblockRec(i,j);
end;
...
Conclusion
I got a “complete” working algorithm that can be used to find all the maze walks. The latest in speed exceeded all expectations. I hope my little work will benefit someone or encourage new thoughts.
The program code and the maze traversed:

//Прошу не бить ногами за использованный язык программирования.
unit Unit1;
interface
uses
Windows, Graphics, Forms, Dialogs, ExtCtrls, StdCtrls, Controls, Classes;
const
WALL=-1;
BLANK=-2;
DEADBLOCK=-3;
type
TForm1 = class(TForm)
Button1: TButton;
OpenDialog1: TOpenDialog;
procedure Button1Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
N:integer=600;
LABIRINT:array[0..600,0..600] of integer;
implementation
{$R *.dfm}
procedure genBitmap;
var bit:TBitmap;
i,j:Integer;
begin
bit:=TBitmap.Create;
bit.Width:=N+1;
bit.Height:=N+1;
for i:=0 to N do
for j:=0 to N do
begin
if LABIRINT[i,j]=BLANK then bit.Canvas.Pixels[i,j]:=clWhite //
else
if LABIRINT[i,j]=WALL then bit.Canvas.Pixels[i,j]:=clBlack
else bit.Canvas.Pixels[i,j]:=clRed;
end;
bit.SaveToFile('tmp.bmp');
bit.Free;
end;
procedure rebuildArr2;
var i,j:integer;
begin
for i:=0 to ((N div 3) ) do
for j:=0 to ((N div 3) ) do
LABIRINT[i,j]:=LABIRINT[i*3,j*3];
N:=N div 3;
end;
procedure setBlankAsDeadblockRec(x,y:integer);
var k:integer;
begin
k:=0;
if LABIRINT[x,y]=blank then
begin
if LABIRINT[x-1,y]<>BLANK then k:=k+1;
if LABIRINT[x,y-1]<>BLANK then k:=k+1;
if LABIRINT[x+1,y]<>BLANK then k:=k+1;
if LABIRINT[x,y+1]<>BLANK then k:=k+1;
if k=4 then LABIRINT[x,y]:=DEADBLOCK;
if k=3 then
begin
LABIRINT[x,y]:=DEADBLOCK;
if LABIRINT[x-1,y]=BLANK then setBlankAsDeadblockRec(x-1,y);
if LABIRINT[x,y-1]=BLANK then setBlankAsDeadblockRec(x,y-1);
if LABIRINT[x+1,y]=BLANK then setBlankAsDeadblockRec(x+1,y);
if LABIRINT[x,y+1]=BLANK then setBlankAsDeadblockRec(x,y+1);
end;
end;
end;
procedure setDeadblock;
var i,j:integer;
begin
for i:=1 to N-1 do
for j:=1 to N-1 do
setBlankAsDeadblockRec(i,j);
end;
procedure TForm1.Button1Click(Sender: TObject);
var bit:TBitmap;
i,j:integer;
begin
bit:=TBitmap.Create;
If OpenDialog1.Execute then
begin
bit.LoadFromFile(OpenDialog1.FileName);
for i:=0 to N do
for j:=0 to N do
if bit.Canvas.Pixels[j,i]=clWhite then
LABIRINT[j,i]:=BLANK else LABIRINT[j,i]:=WALL;
bit.Free;
setDeadblock;
genBitmap;
end;
end;
end.

To find the shortest path, it is planned to apply the wave algorithm to the found maze walks. It would be interesting to hear what other algorithms can be used to quickly find a path in a large maze?
