Meet the Windows pseudo console (ConPTY)
- Transfer
Article published on August 2, 2018
This is the second article about the Windows command line, where we discuss the new Windows infrastructure and software interfaces, that is, Windows Pseudo Console (ConPTY): why we developed it, what it is for, how it works, how to use it and much more.
In the last article “The heavy legacy of the past. Windows command line problems ”, we talked about the prerequisites for the emergence of the terminal and the evolution of the command line in Windows, and also began to study the internal structure of the Windows Console and the Windows Command-Line infrastructure. We also discussed the many advantages and major disadvantages of the Windows console.
One of the drawbacks is that Windows tries to be “useful”, but it prevents developers of alternative and third-party consoles, developers of services, etc. When creating a console or service, developers need to have access to communication channels through which their terminal / service communicates with command line applications, or provide access to them. In the * NIX world, this is not a problem, because * NIX provides a “pseudo-terminal” (PTY) infrastructure that makes it easy to create communication channels for a console or service. But in Windows this was not ...
... so far!
Before discussing our development in detail, let's briefly return to the development of terminals.
As discussed in the last article , in the early days of computing, users controlled computers using electro-mechanical teletypes (TTY) connected to the computer via some kind of serial communication channel (usually through a 20 mA current loop ).

Ken Thompson and Dennis Richie (standing) work on DEC PDP-11 by teletype (messages without electronic display)
Teletypes were replaced by computerized terminals with electronic displays (usually CRT screens). As a rule, terminals are very simple devices (hence the term “stupid terminal”), containing only electronics and computing power necessary for the following tasks:
Despite the simplicity (or perhaps because of it), terminals quickly became the main tool for managing minicomputers, mainframes and servers: most data entry operators, computer operators, system administrators, scientists, researchers, software developers and industry luminaries worked on DEC terminals, IBM, Wyse and many others.

Admiral Grace Hopper in his office with a DEC VT220 terminal on the table
Since the mid-1980s, instead of specialized terminals, general-purpose computers began to be used, which became more accessible, popular, and powerful. Many early PCs and other computers of the 1980s had terminal applications that opened a connection over an RS-232 port on a PC and communicated with anyone at the other end of the connection.
As general-purpose computers became more sophisticated, a graphical user interface (GUI) and a whole new world of simultaneously running applications, including terminal applications, appeared.
But the problem arose: how can a terminal application interact with another command line application running on the same machine? And how to physically connect a serial cable between two applications running on the same computer?
In the world * NIX, the problem was solved by introducing a pseudo-terminal (PTY) .
PTY emulates serial telecommunications equipment in a computer by exposing the master and slave pseudo-devices (“master” and “slave”): terminal applications connect to the master pseudo-device, and command-line applications (for example, shells like cmd, PowerShell, and bash) to the slave pseudo-device. When a terminal client transmits text and / or control commands (encoded as text) to the master pseudo-device, the text is translated to the associated slave. The text from the application is sent to the slave pseudo-device, then back to the master and, thus, to the terminal. Data is always sent / received asynchronously.
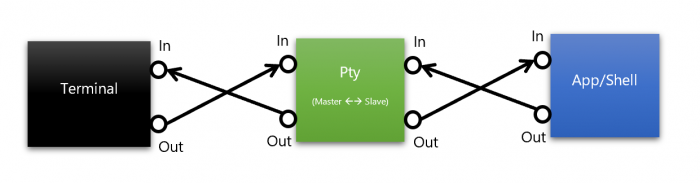
Pseudo-terminal application / shell
It is important to note that the “slave” pseudo-device emulates the behavior of a physical terminal and converts command characters into POSIX signals. For example, if the user enters CTRL + C into the terminal , then the ASCII value for CTRL + C (0x03) is sent through the master device. When received at the slave pseudo-device, the value 0x03 is removed from the input stream and a SIGINT signal is generated .
Such a PTY infrastructure is widely used by * NIX terminal applications, text panel managers (for example, screen, tmux), etc. Application data calls
This mechanism allows terminal applications to "talk" directly with command-line applications running locally, like a terminal would talk to a remote computer via a serial / network connection.
As we discussed in a previous article, while the Windows console is conceptually similar to the traditional * NIX terminal, it differs in several key ways, especially at the lowest levels that can cause problems for developers of Windows command line applications, third-party terminals / consoles, and server applications:
Many, many developers often requested a PTY-like mechanism under Windows, especially those who work with ConEmu / Cmder, Console2 / ConsoleZ, Hyper, VSCode, Visual Studio, WSL, Docker and OpenSSH tools.
Even Peter Bright, Ars Technica’s technology editor, asked to implement the PTY mechanism a few days later, as I started working in the Console team:

And recently, again:

Well, we finally did it: we created a pseudo-console for Windows :
Since the formation of the Console Team about four years ago, the group has been engaged in a major overhaul of the Windows console and the internal mechanisms of the command line. In doing so, we regularly and thoroughly reviewed the issues described above and many other related issues and problems. But the infrastructure and code were not ready to make the release of the pseudo-console possible ... until now!
New Windows pseudo-console infrastructure (ConPTY), API and some other relevant changes will eliminate / ease a whole class of problems ... without breaking backward compatibility with existing command line applications !
To understand ConPTY, you need to study the architecture of the Windows console, or rather ... ConHost!
It is important to understand that although ConHost implements everything you see and know as a Windows Console application, but ConHost also contains and implements most of the Windows command line infrastructure! From now on, ConHost becomes a real “console node” , supporting all command line applications and / or GUI applications that interact with command line applications!
How? Why? What? Let's take a closer look.
Here is a high-level view of the internal architecture of the console / ConHost:
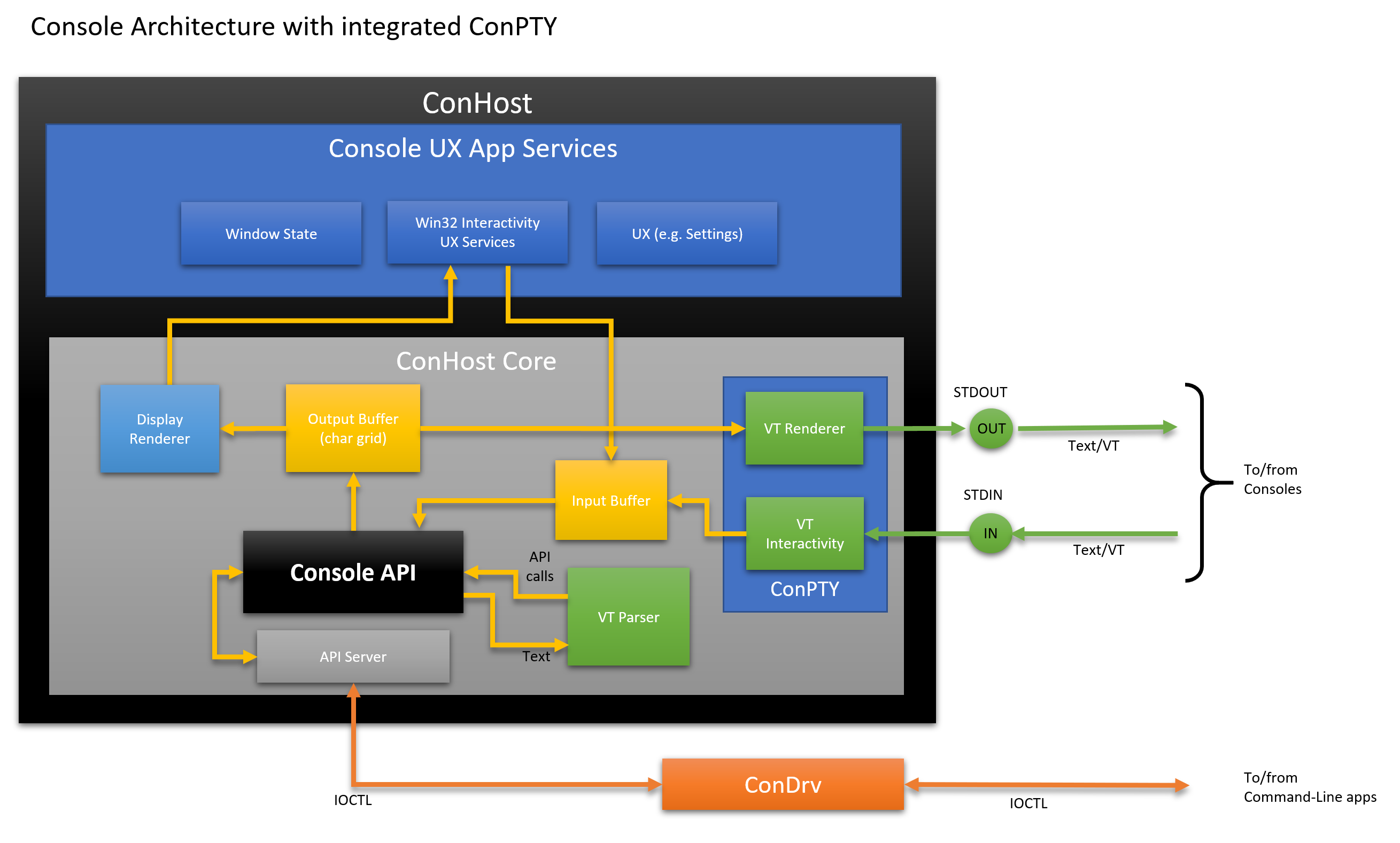
Compared to the architecture from the previous articleConHost now contains several additional modules for processing VT and a new ConPTY module that implements open APIs:
OK, but what does that really mean?
To better understand the impact of the new ConPTY infrastructure, let's look at how Windows console and command-line applications have worked so far.
Whenever a user starts a command-line application, such as Cmd, PowerShell, or ssh, Windows creates a new Win32 process into which it loads the executable binary of the application and any dependencies (resources or libraries).
The newly created process usually inherits the stdin and stdout descriptors from its parent. If the parent process was a Windows GUI process, then the stdin and stdout handles are missing, so Windows will deploy and attach the new application to the new console instance. Communication between command line applications and their console is passed through ConDrv.
For example, when starting from a PowerShell instance without elevated rights, a new application process will inherit the parent stdin / stdout descriptors and, therefore, will receive input data and output the output data to the same console as the parent.
Ultimately, when a command-line / shell application starts, Windows connects it to the console instance (ConHost.exe) via ConDrv:
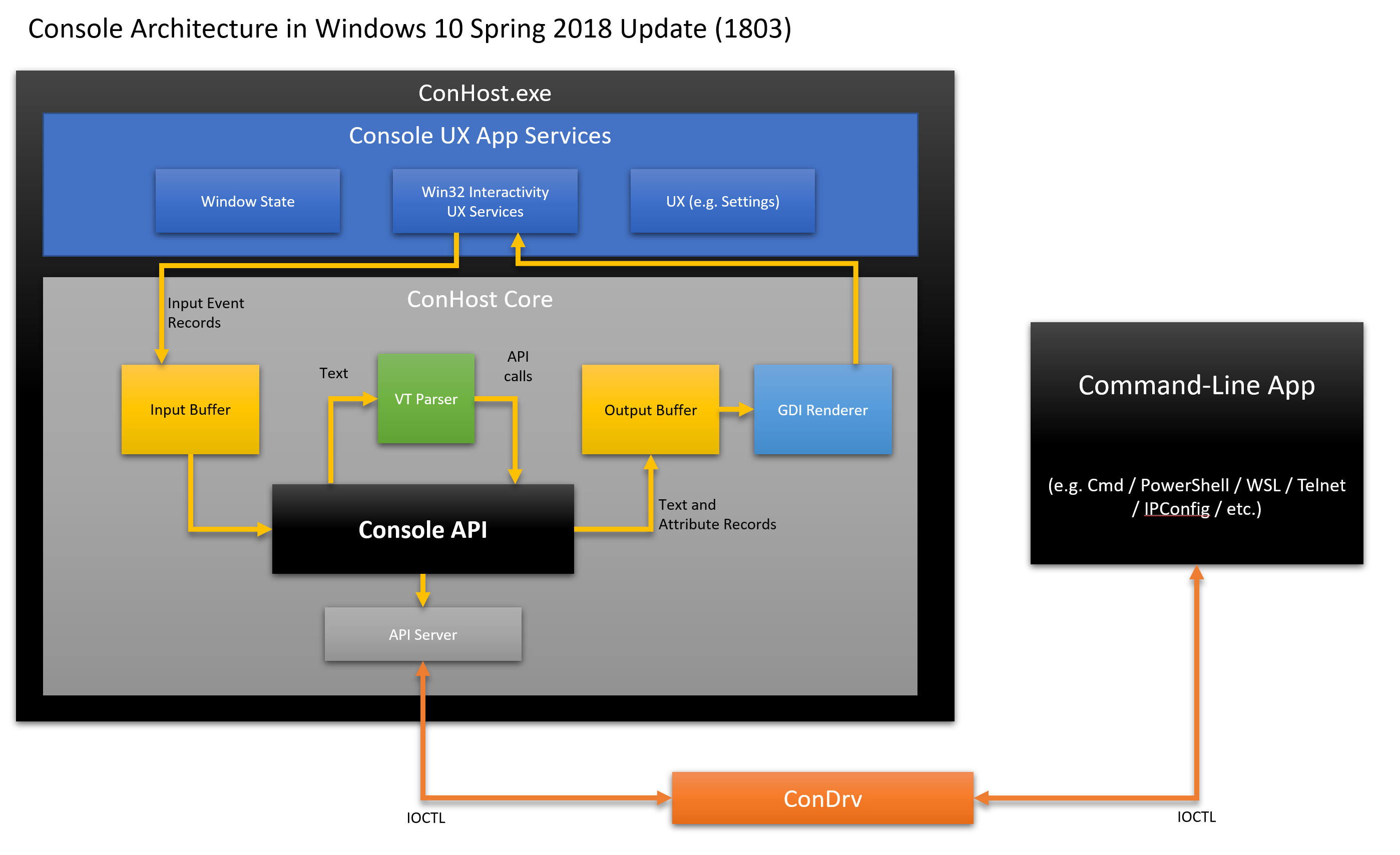
Whenever a command line application is executed, Windows connects the application to a new or existing instance of ConHost. An application and its console instance are connected via the kernel-mode console driver (ConDrv), which sends / receives IOCTL messages containing serialized API call requests and / or text data.
Historically, as stated in the previous article, the work of ConHost is relatively simple today:
When a command line application calls the Windows Console API, API calls are serialized into IOCTL messages and sent via the ConDrv driver. It then delivers the IOCTL messages to the attached console, which decodes and makes the requested API call. Returned / output values are serialized back to the IOCTL message and sent back to the application via ConDrv.
Microsoft tries to maintain backward compatibility with existing applications and tools whenever possible. Especially for the command line. In fact, 32-bit versions of Windows 10 can still run many / most 16-bit Win16 applications and executables!
As mentioned above, one of the key roles of ConHost is to provide services to its command-line applications, especially legacy applications that call and rely on the Win32 console API. ConHost now offers new services:
Below is an example of how a modern console application communicates with a command line application via ConPTY ConHost.
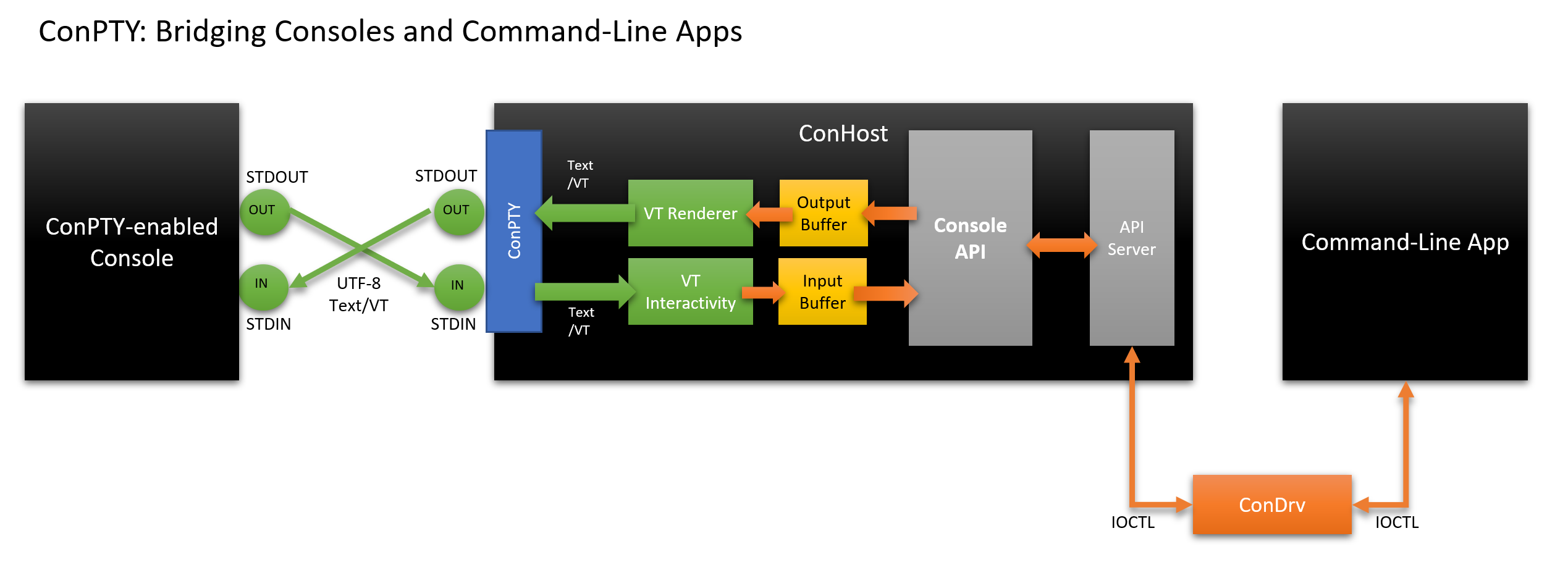
In this new model:
The last moment is important! When an old command-line application uses calls to the Console API like this
In the end, even traditional command-line applications from the outside “speak” with text / VT without any changes !
Using the new ConPTY infrastructure, third-party consoles can now directly interact with modern and traditional command-line applications and exchange data with all of them in the text / VT.
The mechanism described above works fine on one computer, but also helps in interacting, for example, with a PowerShell instance on a remote Windows computer or in a container.
When you run the command line application remotely (that is, on remote computers, servers, or in containers), there is a problem. The point is that command-line applications on remote machines communicate with the local ConHost instance, because IOCTL messages are not intended to be transmitted over the network. How to transfer input from the local console to a remote machine and how to get output from the application running there? Moreover, what to do with Mac and Linux machines, where there are terminals, but no Windows-compatible consoles?
Thus, in order to remotely control a Windows machine, we need some kind of communication broker that can transparently serialize data across the network, control the lifetime of the application instance, etc.
Maybe something like ssh ?
Fortunately, OpenSSH recently ported to Windows and added Windows 10 as an additional option . PowerShell Core also uses ssh as one of the supported protocols for remote interaction PowerShell Core Remoting . And for those who worked in Windows PowerShell, remoting Windows PowerShell remoting is still an acceptable option.
Let's see how nowOpenSSH for Windows allows you to remotely control Windows shells and applications on the Windows command line:
Currently, OpenSSH includes some unwanted complications:
Fun, right? Not at all! In such a situation, much can go awry, especially in the process of simulating and sending user input and clearing the output buffer of an offscreen console. This leads to instability, failure, data corruption, excessive energy consumption, etc. In addition, not all applications do the job of removing not only the text itself, but also its properties, due to which formatting and color are lost!
Surely we can improve the situation? Yes, of course, we can - let's make a few architectural changes and apply our new ConPTY:
The diagram shows that the scheme has changed as follows:
This approach with ConPTY is clearly cleaner and easier for the sshd service. Windows Console API calls are made entirely in the ConHost instance of the command line application, which converts all visible changes to text / VT. Whoever connects to ConHost doesn’t need to know that the application is calling the Console API, and does not generate text / VT!
Agree that this new mechanism of remote interaction ConPTY leads to an elegant, consistent and simple architecture. Combined with the powerful features built into ConHost, support for older applications, and the display of changes from applications that invoke the console Console API as text / VT, the new ConHost and ConPTY infrastructure helps us move the past into the future.
By now, I’m sure that you’re looking forward to seeing some code;)
Take a look at the API declarations:
The above API ConPTY essentially exposes three new functions for use:
This is the second article about the Windows command line, where we discuss the new Windows infrastructure and software interfaces, that is, Windows Pseudo Console (ConPTY): why we developed it, what it is for, how it works, how to use it and much more.
In the last article “The heavy legacy of the past. Windows command line problems ”, we talked about the prerequisites for the emergence of the terminal and the evolution of the command line in Windows, and also began to study the internal structure of the Windows Console and the Windows Command-Line infrastructure. We also discussed the many advantages and major disadvantages of the Windows console.
One of the drawbacks is that Windows tries to be “useful”, but it prevents developers of alternative and third-party consoles, developers of services, etc. When creating a console or service, developers need to have access to communication channels through which their terminal / service communicates with command line applications, or provide access to them. In the * NIX world, this is not a problem, because * NIX provides a “pseudo-terminal” (PTY) infrastructure that makes it easy to create communication channels for a console or service. But in Windows this was not ...
... so far!
From TTY to PTY
Before discussing our development in detail, let's briefly return to the development of terminals.
TTY was first
As discussed in the last article , in the early days of computing, users controlled computers using electro-mechanical teletypes (TTY) connected to the computer via some kind of serial communication channel (usually through a 20 mA current loop ).

Ken Thompson and Dennis Richie (standing) work on DEC PDP-11 by teletype (messages without electronic display)
Terminal distribution
Teletypes were replaced by computerized terminals with electronic displays (usually CRT screens). As a rule, terminals are very simple devices (hence the term “stupid terminal”), containing only electronics and computing power necessary for the following tasks:
- Receive text input from the keyboard.
- Buffering of the entered text on one line (including local editing before sending).
- Sending / receiving text over a serial channel (usually via the once-wide RS-232 interface ).
- Display of the received text on the terminal display.
Despite the simplicity (or perhaps because of it), terminals quickly became the main tool for managing minicomputers, mainframes and servers: most data entry operators, computer operators, system administrators, scientists, researchers, software developers and industry luminaries worked on DEC terminals, IBM, Wyse and many others.

Admiral Grace Hopper in his office with a DEC VT220 terminal on the table
Distribution of software terminals
Since the mid-1980s, instead of specialized terminals, general-purpose computers began to be used, which became more accessible, popular, and powerful. Many early PCs and other computers of the 1980s had terminal applications that opened a connection over an RS-232 port on a PC and communicated with anyone at the other end of the connection.
As general-purpose computers became more sophisticated, a graphical user interface (GUI) and a whole new world of simultaneously running applications, including terminal applications, appeared.
But the problem arose: how can a terminal application interact with another command line application running on the same machine? And how to physically connect a serial cable between two applications running on the same computer?
The emergence of a pseudo terminal (PTY)
In the world * NIX, the problem was solved by introducing a pseudo-terminal (PTY) .
PTY emulates serial telecommunications equipment in a computer by exposing the master and slave pseudo-devices (“master” and “slave”): terminal applications connect to the master pseudo-device, and command-line applications (for example, shells like cmd, PowerShell, and bash) to the slave pseudo-device. When a terminal client transmits text and / or control commands (encoded as text) to the master pseudo-device, the text is translated to the associated slave. The text from the application is sent to the slave pseudo-device, then back to the master and, thus, to the terminal. Data is always sent / received asynchronously.

Pseudo-terminal application / shell
It is important to note that the “slave” pseudo-device emulates the behavior of a physical terminal and converts command characters into POSIX signals. For example, if the user enters CTRL + C into the terminal , then the ASCII value for CTRL + C (0x03) is sent through the master device. When received at the slave pseudo-device, the value 0x03 is removed from the input stream and a SIGINT signal is generated .
Such a PTY infrastructure is widely used by * NIX terminal applications, text panel managers (for example, screen, tmux), etc. Application data calls
openpty()which returns a pair of file descriptors (fd) for the master and slave PTY. The application can then fork / run a child command line application (for example, bash), which uses its slave fd to listen and return text to the connected terminal. This mechanism allows terminal applications to "talk" directly with command-line applications running locally, like a terminal would talk to a remote computer via a serial / network connection.
What, no windows pseudo-console?
As we discussed in a previous article, while the Windows console is conceptually similar to the traditional * NIX terminal, it differs in several key ways, especially at the lowest levels that can cause problems for developers of Windows command line applications, third-party terminals / consoles, and server applications:
- There is no PTY infrastructure in Windows : when a user starts a command line application (for example, Cmd, PowerShell, wsl, ipconfig, etc.), Windows itself “connects” a new or existing console instance to the application.
- Windows interferes with third-party consoles and server applications : Windows (for the time being) does not provide terminals with a way to provide communication channels through which they want to interact with a command line application. Third-party terminals have to create a console off-screen, send user-entered data and scrap the output, redrawing it on the third-party console's own display!
- Only in Windows is the Console API : Windows command line applications rely on the Win32 Consol API, which reduces code portability, since all other platforms support the text / VT, and not the API.
- Non-standard remote access : dependence of command line applications on Consol API significantly complicates interaction and remote access scripts.
What to do?
Many, many developers often requested a PTY-like mechanism under Windows, especially those who work with ConEmu / Cmder, Console2 / ConsoleZ, Hyper, VSCode, Visual Studio, WSL, Docker and OpenSSH tools.
Even Peter Bright, Ars Technica’s technology editor, asked to implement the PTY mechanism a few days later, as I started working in the Console team:

And recently, again:

Well, we finally did it: we created a pseudo-console for Windows :
Welcome to the Windows pseudo console (ConPTY)
Since the formation of the Console Team about four years ago, the group has been engaged in a major overhaul of the Windows console and the internal mechanisms of the command line. In doing so, we regularly and thoroughly reviewed the issues described above and many other related issues and problems. But the infrastructure and code were not ready to make the release of the pseudo-console possible ... until now!
New Windows pseudo-console infrastructure (ConPTY), API and some other relevant changes will eliminate / ease a whole class of problems ... without breaking backward compatibility with existing command line applications !
New Win32 ConPTY APIs (official documentation will be published soon) are now available in the latest Windows 10 Insider builds and the corresponding Windows 10 Insider Preview SDK . They will appear in the next major release of Windows 10 (somewhere in autumn / winter 2018).
Console architecture / conhost
To understand ConPTY, you need to study the architecture of the Windows console, or rather ... ConHost!
It is important to understand that although ConHost implements everything you see and know as a Windows Console application, but ConHost also contains and implements most of the Windows command line infrastructure! From now on, ConHost becomes a real “console node” , supporting all command line applications and / or GUI applications that interact with command line applications!
How? Why? What? Let's take a closer look.
Here is a high-level view of the internal architecture of the console / ConHost:

Compared to the architecture from the previous articleConHost now contains several additional modules for processing VT and a new ConPTY module that implements open APIs:
- ConPTY API : The new Win32 ConPTY APIs provide a mechanism similar to the POSIX PTY model, but refracted from Windows.
- VT Interactivity : Receives incoming text encoded in UTF-8, converts each displayed text character to the corresponding record,
INPUT_RECORDand saves it in the input buffer. It also processes control sequences, such as 0x03 (CTRL + C), converting them into onesKEY_EVENT_RECORDSthat produce the corresponding control action. - VT Renderer : generates VT sequences needed to move the cursor and render text and style in the output buffer areas that have changed from the previous frame.
OK, but what does that really mean?
How do Windows command line applications work?
To better understand the impact of the new ConPTY infrastructure, let's look at how Windows console and command-line applications have worked so far.
Whenever a user starts a command-line application, such as Cmd, PowerShell, or ssh, Windows creates a new Win32 process into which it loads the executable binary of the application and any dependencies (resources or libraries).
The newly created process usually inherits the stdin and stdout descriptors from its parent. If the parent process was a Windows GUI process, then the stdin and stdout handles are missing, so Windows will deploy and attach the new application to the new console instance. Communication between command line applications and their console is passed through ConDrv.
For example, when starting from a PowerShell instance without elevated rights, a new application process will inherit the parent stdin / stdout descriptors and, therefore, will receive input data and output the output data to the same console as the parent.
We need to make a little reservation here, because in some cases command-line applications are launched attached to a new console instance, especially for security reasons, but the description above is usually correct.
Ultimately, when a command-line / shell application starts, Windows connects it to the console instance (ConHost.exe) via ConDrv:

How does ConHost work?
Whenever a command line application is executed, Windows connects the application to a new or existing instance of ConHost. An application and its console instance are connected via the kernel-mode console driver (ConDrv), which sends / receives IOCTL messages containing serialized API call requests and / or text data.
Historically, as stated in the previous article, the work of ConHost is relatively simple today:
- The user generates input from the keyboard / mouse / pen / touchpad, which is converted to
KEY_EVENT_RECORDorMOUSE_EVENT_RECORDstored in the input buffer. - The input buffer empties one entry at a time, performing the requested input actions, such as displaying text on the screen, moving the cursor, copying / pasting text, etc. Many of these actions change the contents of the output buffer. These modified areas are recorded by the ConHost state engine.
- In each frame, the console displays the modified areas of the output buffer.
When a command line application calls the Windows Console API, API calls are serialized into IOCTL messages and sent via the ConDrv driver. It then delivers the IOCTL messages to the attached console, which decodes and makes the requested API call. Returned / output values are serialized back to the IOCTL message and sent back to the application via ConDrv.
ConHost: a contribution to the past for the sake of the future
Microsoft tries to maintain backward compatibility with existing applications and tools whenever possible. Especially for the command line. In fact, 32-bit versions of Windows 10 can still run many / most 16-bit Win16 applications and executables!
As mentioned above, one of the key roles of ConHost is to provide services to its command-line applications, especially legacy applications that call and rely on the Win32 console API. ConHost now offers new services:
- Seamless PTY-like infrastructure for communicating with modern consoles and terminals
- Modernize legacy / traditional command line applications
- Receiving and converting UTF-8 text / VT to input records (as if entered by the user)
- Calls to the console API for a hosted application, updating its output buffer accordingly.
- Display of modified output buffer areas in UTF-8 encoding, text / VT
Below is an example of how a modern console application communicates with a command line application via ConPTY ConHost.

In this new model:
- Console:
- Creates own communication channels
- Calls the ConPTY API to create a ConPTY, forcing Windows to start an instance of ConHost connected to the other end of the channels.
- Creates an instance of a command line application (for example, PowerShell) connected to ConHost, as usual
- ConHost:
- Reads UTF-8 text / VT at the input and converts it to records
INPUT_RECORDthat are sent to the command line application. - Performs API calls from a command line application that can modify the contents of the output buffer.
- Displays changes in the output buffer in UTF-8 encoding (text / VT) and sends the resulting text to its console.
- Reads UTF-8 text / VT at the input and converts it to records
- Command line application:
- It works as usual, reads input data and calls the Console API, having no idea what its ConPTY ConHost translates input and output from / to UTF-8!
The last moment is important! When an old command-line application uses calls to the Console API like this
WriteConsoleOutput(...), the specified text is written to the corresponding ConHost output buffer. ConHost periodically displays the changed output buffer areas as text / VT, which is sent back to the console via stdout. In the end, even traditional command-line applications from the outside “speak” with text / VT without any changes !
Using the new ConPTY infrastructure, third-party consoles can now directly interact with modern and traditional command-line applications and exchange data with all of them in the text / VT.
Remote interaction with Windows command line applications
The mechanism described above works fine on one computer, but also helps in interacting, for example, with a PowerShell instance on a remote Windows computer or in a container.
When you run the command line application remotely (that is, on remote computers, servers, or in containers), there is a problem. The point is that command-line applications on remote machines communicate with the local ConHost instance, because IOCTL messages are not intended to be transmitted over the network. How to transfer input from the local console to a remote machine and how to get output from the application running there? Moreover, what to do with Mac and Linux machines, where there are terminals, but no Windows-compatible consoles?
Thus, in order to remotely control a Windows machine, we need some kind of communication broker that can transparently serialize data across the network, control the lifetime of the application instance, etc.
Maybe something like ssh ?
Fortunately, OpenSSH recently ported to Windows and added Windows 10 as an additional option . PowerShell Core also uses ssh as one of the supported protocols for remote interaction PowerShell Core Remoting . And for those who worked in Windows PowerShell, remoting Windows PowerShell remoting is still an acceptable option.
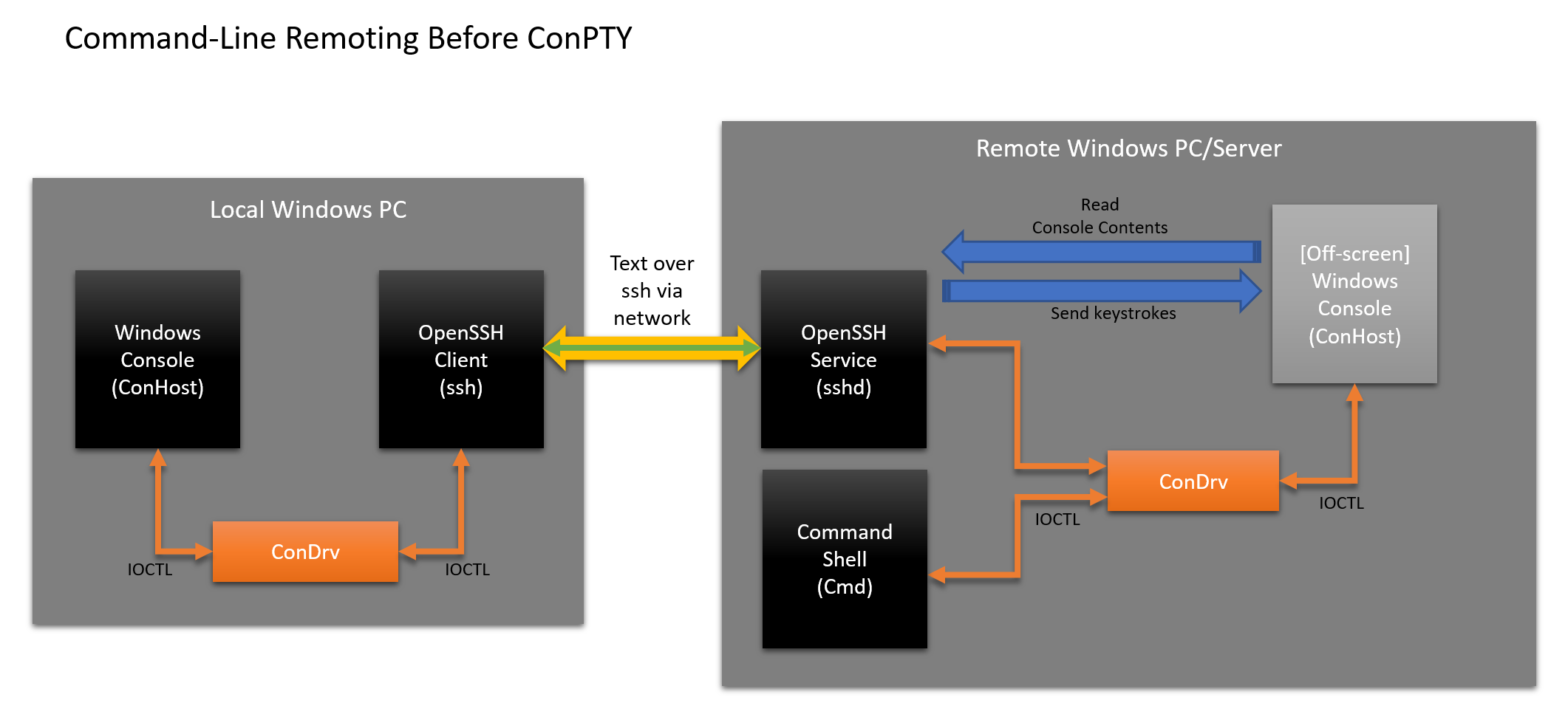
Let's see how nowOpenSSH for Windows allows you to remotely control Windows shells and applications on the Windows command line:

Currently, OpenSSH includes some unwanted complications:
- User:
- Starts the ssh client, and Windows connects the console instance as usual.
- Enters text into the console that sends keystrokes to the ssh client
- ssh client:
- Reads input as bytes of text data.
- Sends text data over the network to the sshd listening service
- The sshd service goes through several stages:
- Runs a default shell (for example, Cmd) that causes Windows to create and mount a new console instance.
- Finds and connects to the Cmd instance console.
- Moves the console off-screen (and / or hides it)
- Sends input from an ssh client to an off-screen console as input.
- The cmd instance works as always:
- Collects input from sshd service
- Performs work
- Causes the Console API to output / style text, move the cursor, etc.
- Attached [offscreen] console:
- Performs API calls, updating the output buffer
- Sshd service:
- Squires off-screen console output buffer, finds differences, encodes them into text / VT and sends back ...
- The ssh client that sends the text ...
- The console that displays text
Fun, right? Not at all! In such a situation, much can go awry, especially in the process of simulating and sending user input and clearing the output buffer of an offscreen console. This leads to instability, failure, data corruption, excessive energy consumption, etc. In addition, not all applications do the job of removing not only the text itself, but also its properties, due to which formatting and color are lost!
Remote operation using modern ConHost and ConPTY
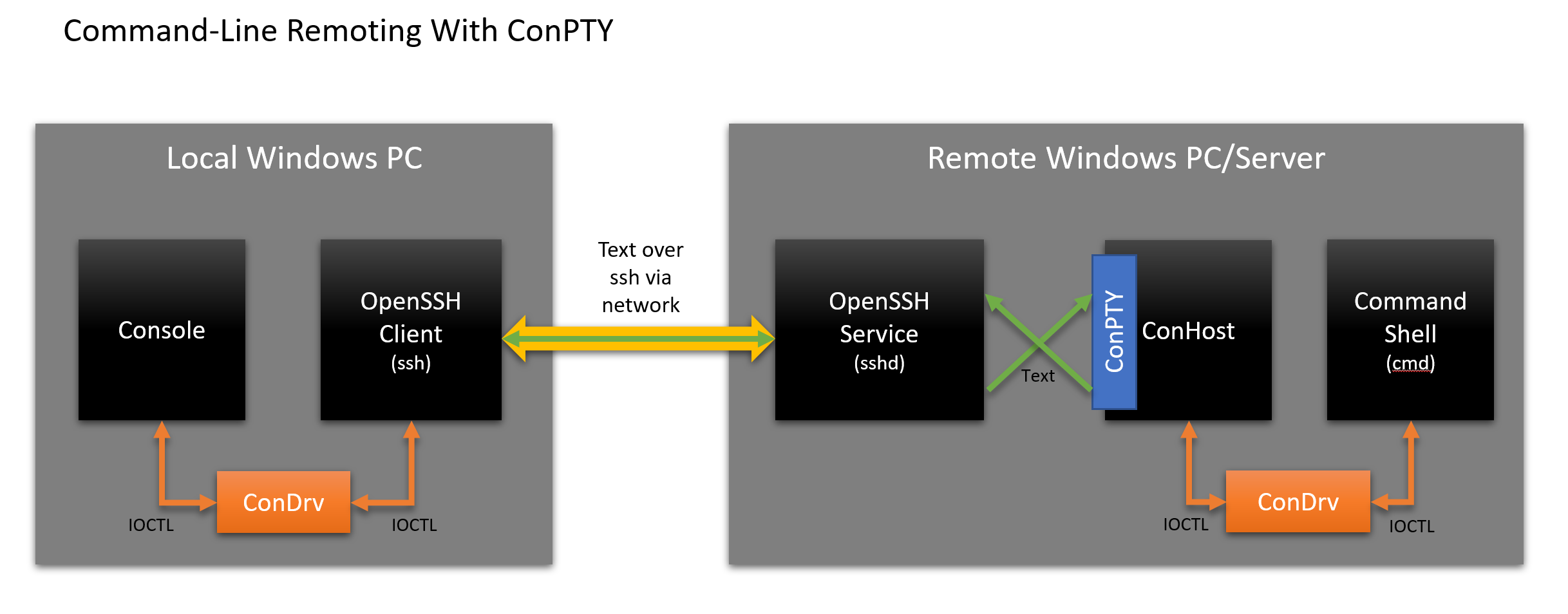
Surely we can improve the situation? Yes, of course, we can - let's make a few architectural changes and apply our new ConPTY:

The diagram shows that the scheme has changed as follows:
- User:
- Starts the ssh client, and Windows connects the console instance as usual.
- Enters text into the console that sends keystrokes to the ssh client
- ssh client:
- Reads input as bytes of text data.
- Sends text data over the network to the sshd listening service
- Sshd service:
- Creates stdin / stdout channels
- Calls the ConPTY API to initiate ConPTY
- Runs a Cmd instance connected to the other end of the ConPTY. Windows initiates and connects a new instance of ConHost
- The cmd instance works as always:
- Collects input from sshd service
- Performs work
- Causes the Console API to output / style text, move the cursor, etc.
- ConPTY ConHost instance:
- Performs API calls, updating the output buffer
- Displays changed output buffer regions as text / VT in UTF-8 encoding, which is sent back to the console / terminal via ssh
This approach with ConPTY is clearly cleaner and easier for the sshd service. Windows Console API calls are made entirely in the ConHost instance of the command line application, which converts all visible changes to text / VT. Whoever connects to ConHost doesn’t need to know that the application is calling the Console API, and does not generate text / VT!
Agree that this new mechanism of remote interaction ConPTY leads to an elegant, consistent and simple architecture. Combined with the powerful features built into ConHost, support for older applications, and the display of changes from applications that invoke the console Console API as text / VT, the new ConHost and ConPTY infrastructure helps us move the past into the future.
ConPTY API and how to use it
The ConPTY API is available in the current version of the Windows 10 Insider Preview SDK .
By now, I’m sure that you’re looking forward to seeing some code;)
Take a look at the API declarations:
// Creates a "Pseudo Console" (ConPTY).HRESULT WINAPI CreatePseudoConsole(
_In_ COORD size, // ConPty Dimensions
_In_ HANDLE hInput, // ConPty Input
_In_ HANDLE hOutput, // ConPty Output
_In_ DWORD dwFlags, // ConPty Flags
_Out_ HPCON* phPC); // ConPty Reference// Resizes the given ConPTY to the specified size, in characters.HRESULT WINAPI ResizePseudoConsole(_In_ HPCON hPC, _In_ COORD size);
// Closes the ConPTY and all associated handles. Client applications attached // to the ConPTY will also terminated. VOID WINAPI ClosePseudoConsole(_In_ HPCON hPC);The above API ConPTY essentially exposes three new functions for use:
CreatePseudoConsole(size, hInput, hOutput, dwFlags, phPC)- Creates a pty dimension in
wcolumns andhrows using channels created by the caller:size: width and height (in characters) of the ConPTY bufferhInput: to write input data to PTY as text / VT sequences in UTF-8hOutput: to read the output from PTY as text / VT sequences in UTF-8dwFlags: Possible values:PSEUDOCONSOLE_INHERIT_CURSOR: The created ConPTY will try to inherit the cursor position of the parent terminal application
phPC: console descriptor for created ConPty
- Returns : success / failure. If successful, phPC contains a handle to the new ConPty.
ResizePseudoConsole(hPC, size)- Changes the size of the internal ConPTY buffer to display a specific width and height.
ClosePseudoConsole (hPC)- Closes ConPTY and all associated handles. Client applications connected to ConPTY are also terminated as if they were running in a console window that is closing.
Using the ConPTY API
Below is a small example of the ConPTY API call code for creating a pseudo-console and attaching a command line application to the ConPTY created.Note: the full implementation will be published in our GitHub repository.
// Note: Most error checking removed for brevity.// ...// Initializes the specified startup info struct with the required properties and// updates its thread attribute list with the specified ConPTY handleHRESULT InitializeStartupInfoAttachedToConPTY(STARTUPINFOEX* siEx, HPCON hPC){ HRESULT hr = E_UNEXPECTED; size_t size; siEx->StartupInfo.cb = sizeof(STARTUPINFOEX); // Create the appropriately sized thread attribute list InitializeProcThreadAttributeList(NULL, 1, 0, &size); std::unique_ptr<BYTE[]> attrList = std::make_unique<BYTE[]>(size); // Set startup info's attribute list & initialize it siEx->lpAttributeList = reinterpret_cast<PPROC_THREAD_ATTRIBUTE_LIST>( attrList.get()); bool fSuccess = InitializeProcThreadAttributeList( siEx->lpAttributeList, 1, 0, (PSIZE_T)&size); if (fSuccess) { // Set thread attribute list's Pseudo Console to the specified ConPTY fSuccess = UpdateProcThreadAttribute( lpAttributeList, 0, PROC_THREAD_ATTRIBUTE_PSEUDOCONSOLE, hPC, sizeof(HPCON), NULL, NULL); return fSuccess ? S_OK : HRESULT_FROM_WIN32(GetLastError()); } else { hr = HRESULT_FROM_WIN32(GetLastError()); } return hr; } // ... HANDLE hOut, hIn; HANDLE outPipeOurSide, inPipeOurSide; HANDLE outPipePseudoConsoleSide, inPipePseudoConsoleSide; HPCON hPC = 0; // Create the in/out pipes: CreatePipe(&inPipePseudoConsoleSide, &inPipeOurSide, NULL, 0); CreatePipe(&outPipeOurSide, &outPipePseudoConsoleSide, NULL, 0); // Create the Pseudo Console, using the pipes CreatePseudoConsole( {80, 32}, inPipePseudoConsoleSide, outPipePseudoConsoleSide, 0, &hPC); // Prepare the StartupInfoEx structure attached to the ConPTY. STARTUPINFOEX siEx{}; InitializeStartupInfoAttachedToConPTY(&siEx, hPC); // Create the client application, using startup info containing ConPTY infowchar_t* commandline = L"c:\\windows\\system32\\cmd.exe"; PROCESS_INFORMATION piClient{}; fSuccess = CreateProcessW( nullptr, commandline, nullptr, nullptr, TRUE, EXTENDED_STARTUPINFO_PRESENT, nullptr, nullptr, &siEx->StartupInfo, &piClient); // ...
Now cmd.exe is connected to the ConPTY instance createdCreatePseudoConsole(). The caller uses the ConPTY handles it creates to write and read to / from the Cmd instance. The size of the pseudo-console is changed byResizePseudoConsole(), and the closing by callClosePseudoConsole().Record in pseudo console
Writing input to ConPTY is easy:// Input "echo Hello, World!", press enter to have cmd process the command, // input an up arrow (toget the previous command), and enter again toexecute. std::string helloWorld = "echo Hello, World!\n\x1b[A\n"; DWORD dwWritten; WriteFile(hIn, helloWorld.c_str(), (DWORD)helloWorld.length(), &dwWritten, nullptr);Resizing pseudoconsoli
The following script shows how to resize a ConPTY:// Suppose some other async callback triggered us to resize.// This call will update the Terminal with the size we received. HRESULT hr = ResizePseudoConsole(hPC, {120, 30});Pseudoconsoli close
There is nothing easier than closing ConPTY:ClosePseudoConsole(hPC);
Note: closing ConPTY will complete the associated ConHost and any attached clients.Call to action!
The introduction of the ConPTY API is probably one of the most fundamental and liberating changes that have occurred to the Windows command line in recent years ... if not decades !
We have already ported some Microsoft tools to the ConPTY API, and now we are collaborating with several teams inside Microsoft (Windows subsystem for Linux (WSL), Windows Containers commands, VSCode, Visual Studio, etc.), as well as with some independent developers, including @ ConEmuMaximus5 - the creator of the amazing ConEmu console for Windows.
But we need your help to spread the word and start using the new ConPTY API.Command line application developers
If you have a traditional command line application, then you are free and can do nothing: ConHost will do all the work for you. The program can continue to work as before and rely on calls to the Console API. The application will continue to work as usual, at the same time receiving an additional bonus in the form of an improved, better remote interaction.
But if you want, you can gradually introduce new support for VT, for example, for new functions - you decide.
On the other hand, if you are currently planning new Windows command line applications, we strongly recommend translating the text / VT in UTF-8 encoding instead of accessing the Console API: such a “conversation on VT” will give access to many functions that will not be available via Console API (for example,support 16M RGB True Color ).Developers of third-party consoles / services
If you are working on a standalone console / terminal application or integrating the console into an application, we urge you to learn and adopt the new ConPTY API as soon as possible: using new software interfaces instead of the old off-screen console mechanism will most likely eliminate several classes of errors, while increasing stability, reliability and performance.As an example, the VSCode team is currently resolving an issue ( GitHub # 45693 ) with several problems caused by the current lack of a pseudo-console for Windows.
ConPTY API Detection
New ConPTY API will be available in the release of Windows 10 in the fall / winter of 2018.
To support earlier versions of Windows, you will probably need to check in runtime whether the current version of ConPTY is supported. As with most Win32 APIs, an effective way to check for APIs is to use the Runtime Dynamic Linking method by callingLoadLibrary()andGetProcAddress().
If the current version of Windows supports ConPTY, your application will be able to find and call new ConPTY APIs. If not, you will have to go back to the intricate mechanisms used so far.So what are we staying at?
Another long article ... it becomes a habit! Once again, if you could finish reading this place, THANKS ! : D
From the above information we can draw many conclusions, but it is important to emphasize why we make such improvements, as well as the essence of the implemented changes. Our goal is to eliminate a whole class of problems and limitations for developers of console and server applications, as well as to make the development of code for the Windows command line infrastructure more powerful, consistent and fun.
We welcome feedback through the feedback hub . Report more complicated issues to the Windows Console repository on GitHub . And if you have questions, knock me on Twitter .- Creates a pty dimension in
