How to generate random parenthesis sequences
Hello, Habr!
When testing algorithms, I often have the task of generating a random binary tree. Moreover, Wishlist is not reduced to anyhow any random tree, but taken from a uniform distribution. Despite the apparent simplicity, it is completely non-trivial to effectively build such a tree.
The title of this article contains the words “bracket sequence”. Behind these words, something more is hidden, because with the help of brackets you can describe very diverse objects, including binary trees. On Habré a separate post was devoted to this fact .
In this article, I will describe several ways to generate a random bracket sequence, including in linear time, and then give an example of converting a sequence to a binary tree. Interesting?
Given n, generate the correct bracket sequence according to the uniform distribution over all correct sequences of length 2 n .
It is known that the number of regular bracket sequences of length 2 n equals the nth number of Catalan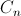 . Explicit
. Explicit

and recursive
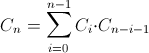
formulas exist to calculate Catalan numbers .
We need a random number generator. Given n , it will generate an equally probable random number from 0 to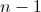 . Also, a random permutation generator over lists is useful to us. In python, it is called random.shuffle. It will be enough for us that it works linear time and generates a random permutation according to the uniform distribution on the sequence 1,2, ..., n .
. Also, a random permutation generator over lists is useful to us. In python, it is called random.shuffle. It will be enough for us that it works linear time and generates a random permutation according to the uniform distribution on the sequence 1,2, ..., n .
There is such an idea that all correct bracket sequences can be numbered. And, for example, there is a detailed description of how to do this. So, you can implement such a plan.
The plan is almost excellent. Those. the plan is very good if n is small, less than 30. But if n turns out to be of the order of 1'000, long arithmetic will be required, cubic time will work by reference instead of the promised square, and in general, dynamic programming is not for you khukh-mukhras. I think I’ll have to sweat a lot to keep up with such a plan at least . Let's look for alternative ways.
. Let's look for alternative ways.
Let's take a look at the explicit formula for Catalan numbers again.
 .
.
In fact, it means that there are a lot of correct bracket sequences.
We say that a sequence is balanced if the number of parentheses that open and close in it is the same. For example, the sequence . If one of these sequences is randomly chosen, then it will be correct with the probability of a
. If one of these sequences is randomly chosen, then it will be correct with the probability of a 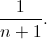
New Plan.
Let's start with the first paragraph: how to generate such a random bracket sequence. Let's take an arbitrary balanced sequence and mix it through random.shuffle.
If you sit with a piece of paper and a pen, you can understand that for any balanced bracket sequence x, there are exactly permutations that translate an arbitrary initial balanced sequence into x . So random.shuffle generates any balanced sequence with equal probability. We get the algorithm.
permutations that translate an arbitrary initial balanced sequence into x . So random.shuffle generates any balanced sequence with equal probability. We get the algorithm.
It remains to evaluate the time. The correct and random.shuffle routines work per line. How many iterations of the main loop will be? We know that the correct bracket sequence is generated with probability . Then we can say that we have a coin in which the eagle drops with probability
. Then we can say that we have a coin in which the eagle drops with probability  . It is necessary to calculate the mat. Waiting for the number of throws until the eagle falls.
. It is necessary to calculate the mat. Waiting for the number of throws until the eagle falls.
As an option, you can paint the mat. Wait by the formula and get something like this:

Or use the well-known facts . One way or another, mat. waiting time for the entire algorithm will be .
.
Ok, but what if we need a really big sequence? Sequence per million characters.
The linear algorithm is no longer so trivial. Back in 1992, a separate article was dedicated to him by Mike Atkinson and Georges Sack. I will present here my vision of what is written in the article.
We need the magic function f . At the input, the function must take a balanced bracket sequence, and at the output, return the correct one of the same length. It is important to make sure that the function scatters the sequences evenly, namely, for every regular sequence y there is exactly n + 1 balanced sequence x , such thatf (x) = y . If the function can be calculated for linear time, then the point is in the hat.
We generate a bracketed balanced sequence x according to the uniform distribution and return f (x).
All the tricks in the function. If you want, you can stop and try to come up with one yourself. It doesn’t work, it's okay. Now I will get a rabbit out of the mathematics world from the cylinder, and everyone will be fine.
Suppose we have a counter, and initially it is zero. Let's go over the sequence. For each opening bracket we will add a point, for each closing bracket - subtract.
The graph below shows how the counter changes
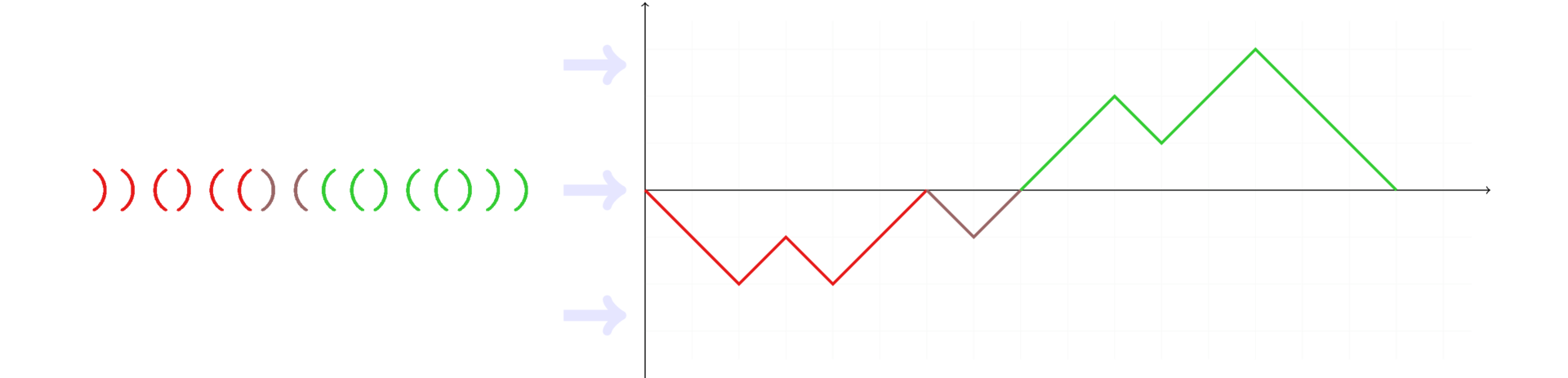
Sequences painted in separate colors are called indecomposable. Those. in general, a sequence is indecomposable if the counter on it assumes a zero value only at the start and end points. You can see that indecomposable sequences fall into two categories: those that are entirely above the zero level, and those that are lower. The former will be called positive sequences, the latter negative.
We calculate the total length of the negative subsequences and divide it in half. The obtained value is called a sequence defect. The correct sequences have zero defect. If we replace all the brackets in the correct sequence of length 2 non the contrary, the defect will be n .
Attention, rabbit! Chang-Feller Theorem. The number of bracket sequences of length 2 n with defect k is equal to the n- th number of Catalan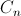 and does not depend on k .
and does not depend on k .
The theorem is interesting in that it divides all balanced sequences of length 2 n into n + 1 classes of the same size, and among the classes there is a separate class containing all the correct bracket sequences. Therefore, we can try to come up with a function that encodes every sequence x with defect k with the correct sequence y, and from the sequence y and the defect k, we could uniquely reconstruct x .
If we manage to come up with such a function, then we get that for every correct sequence there are exactly n + 1 balanced with defects from 0 to n . It seems to be easy.
Let's take all the negative subsequences and invert, i.e. replace the brackets with the opposite.

Plus such a function, it retains the position of all indecomposable sequences. Minus - we lose all information about which subsequence was negative and which was positive. Even knowing that the defect was 3, we cannot restore the initial sequence from the example.
Let's invert all negative subsequences, and then put them to the end.

Now, knowing the defect, we can recover the negative subsequences. But we lost the position where they were.
We take an arbitrary indecomposable negative sequence and tear off its extreme brackets, and invert the result.
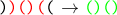
Such an operation is called cunning inversion and denoted by g . Since the sequence is indecomposable and negative, the result will always be the correct bracket sequence. The trick of the function g is that, on the one hand, it is reversible, and on the other, we have two extra brackets that can be used to encode the position of a negative subsequence.
We finish Attempt 2, only now we take out the negative sequences in the reverse order and artfully invert them through the g function :
![\ texttt {() {\ color {red})) ((} (()) {\ color {red}) (}} \ rightarrow \ texttt {() {\ color {blue} \ bf [} (() ) {\ color {blue} \ bf [} {\ color {blue} \ bf]} {\ color {green} e}} _ {\ texttt {\ color {red}) (}} \ texttt {{\ color {blue} \ bf]} {\ color {green} ()}} _ \ texttt {\ color {red})) ((}](https://habrastorage.org/getpro/habr/post_images/e07/77b/0aa/e0777b0aa19cbdad72a0f21933700520.gif)
As you can see from the example, the position of the negative subsequence can be noted by the free brackets. I highlighted them in blue and made them square. The letter e means an empty sequence.
Find out which brackets are green and which blue can be defective, which means that you can restore the initial sequence itself. This is what you need!
Atkinson and Sack proposed a recursive formula for the function f:
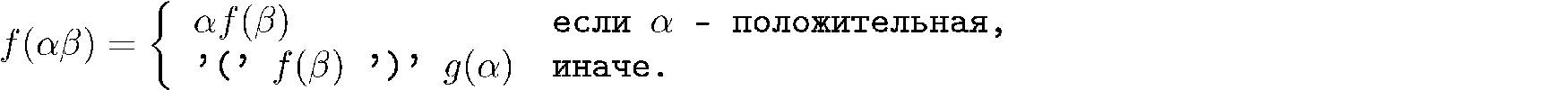
Here is an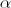 indecomposable subsequence, and
indecomposable subsequence, and 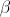 is the remainder.
is the remainder.
Below I am attaching an implementation of the algorithm in Python with expanded recursion. It is easy to understand that the algorithm runs linear time.
If you read to this place, I am very happy. All that remains is to convert the sequence to a tree.
Bracket sequences of length 2 n perfectly encode trees of arbitrary arity with n + 1 vertices. Indeed, let's start a search in depth. At the entrance to the vertex, we write the opening bracket, at the exit - the closing bracket.
At the same time, trees of arbitrary arity from n + 1 can be put in one-to-one correspondence with binary trees from n vertices. All that is needed is to first write down trees of arbitrary arity in the form “left child - right neighbor”, and then rename the right neighbor to the right child.
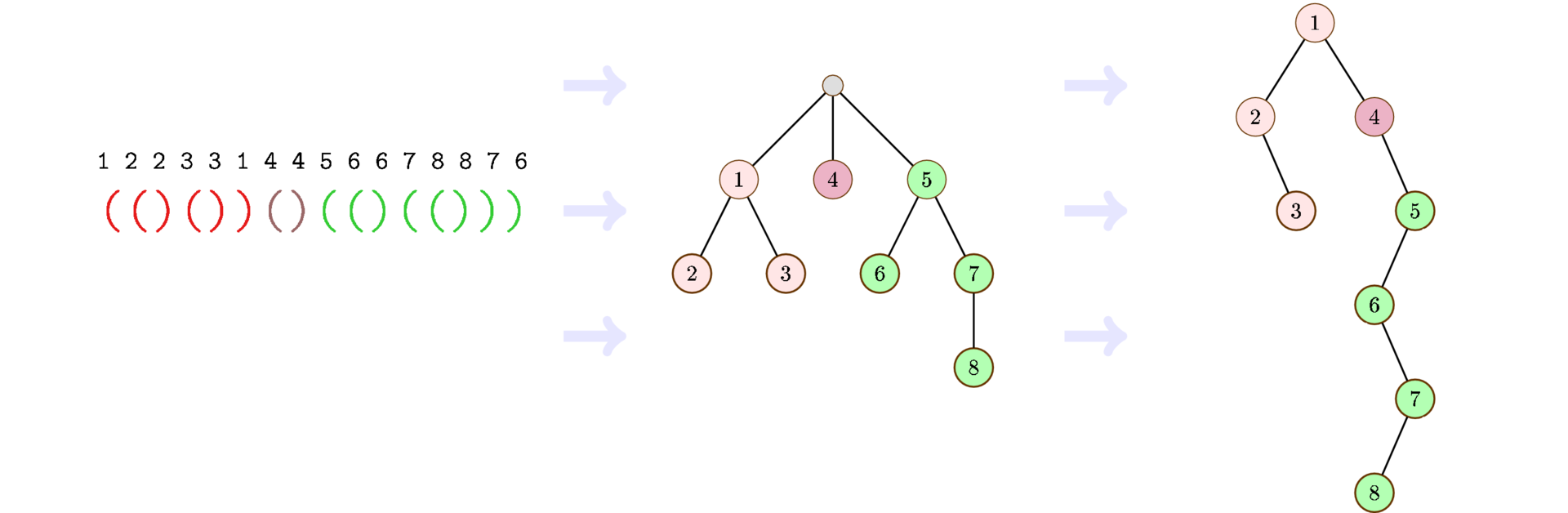
Thank you for being with us!
When testing algorithms, I often have the task of generating a random binary tree. Moreover, Wishlist is not reduced to anyhow any random tree, but taken from a uniform distribution. Despite the apparent simplicity, it is completely non-trivial to effectively build such a tree.
The title of this article contains the words “bracket sequence”. Behind these words, something more is hidden, because with the help of brackets you can describe very diverse objects, including binary trees. On Habré a separate post was devoted to this fact .
In this article, I will describe several ways to generate a random bracket sequence, including in linear time, and then give an example of converting a sequence to a binary tree. Interesting?
Task
Given n, generate the correct bracket sequence according to the uniform distribution over all correct sequences of length 2 n .
Inventory
It is known that the number of regular bracket sequences of length 2 n equals the nth number of Catalan
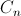 . Explicit
. Explicit 
and recursive
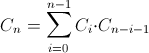
formulas exist to calculate Catalan numbers .
We need a random number generator. Given n , it will generate an equally probable random number from 0 to
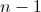 . Also, a random permutation generator over lists is useful to us. In python, it is called random.shuffle. It will be enough for us that it works linear time and generates a random permutation according to the uniform distribution on the sequence 1,2, ..., n .
. Also, a random permutation generator over lists is useful to us. In python, it is called random.shuffle. It will be enough for us that it works linear time and generates a random permutation according to the uniform distribution on the sequence 1,2, ..., n .Three ways to say maybe
The power of dynamic programming
There is such an idea that all correct bracket sequences can be numbered. And, for example, there is a detailed description of how to do this. So, you can implement such a plan.
- We consider the n-th number of Catalan.
- We generate a random number from 1 to
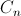 .
. - Using dynamic programming and combinatorial counting, we restore the bracket sequence by its number.
The plan is almost excellent. Those. the plan is very good if n is small, less than 30. But if n turns out to be of the order of 1'000, long arithmetic will be required, cubic time will work by reference instead of the promised square, and in general, dynamic programming is not for you khukh-mukhras. I think I’ll have to sweat a lot to keep up with such a plan at least
 . Let's look for alternative ways.
. Let's look for alternative ways.Try and check
Let's take a look at the explicit formula for Catalan numbers again.
 .
. In fact, it means that there are a lot of correct bracket sequences.
We say that a sequence is balanced if the number of parentheses that open and close in it is the same. For example, the sequence
")(()", "()()"are balanced, and the sequence "()))"- no. Obviously, any correct sequence is balanced. All of all possible balanced sequences of length 2n exist  . If one of these sequences is randomly chosen, then it will be correct with the probability of a
. If one of these sequences is randomly chosen, then it will be correct with the probability of a 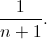
New Plan.
- We generate a random balanced bracket sequence according to the uniform distribution.
- Check it for correctness.
- If the sequence is correct, then we deduce. If not, then return to step 1.
Let's start with the first paragraph: how to generate such a random bracket sequence. Let's take an arbitrary balanced sequence and mix it through random.shuffle.
seq = ['(', ')'] * n
random.shuffle(seq)
If you sit with a piece of paper and a pen, you can understand that for any balanced bracket sequence x, there are exactly
 permutations that translate an arbitrary initial balanced sequence into x . So random.shuffle generates any balanced sequence with equal probability. We get the algorithm.
permutations that translate an arbitrary initial balanced sequence into x . So random.shuffle generates any balanced sequence with equal probability. We get the algorithm.def tryAndCheck(n):
seq = [')', '('] * n
while (not correct(seq)):
random.shuffle(seq)
return seq
It remains to evaluate the time. The correct and random.shuffle routines work per line. How many iterations of the main loop will be? We know that the correct bracket sequence is generated with probability
 . Then we can say that we have a coin in which the eagle drops with probability
. Then we can say that we have a coin in which the eagle drops with probability  . It is necessary to calculate the mat. Waiting for the number of throws until the eagle falls.
. It is necessary to calculate the mat. Waiting for the number of throws until the eagle falls. As an option, you can paint the mat. Wait by the formula and get something like this:

Or use the well-known facts . One way or another, mat. waiting time for the entire algorithm will be
 .
.Try and fix
Ok, but what if we need a really big sequence? Sequence per million characters.
The linear algorithm is no longer so trivial. Back in 1992, a separate article was dedicated to him by Mike Atkinson and Georges Sack. I will present here my vision of what is written in the article.
We need the magic function f . At the input, the function must take a balanced bracket sequence, and at the output, return the correct one of the same length. It is important to make sure that the function scatters the sequences evenly, namely, for every regular sequence y there is exactly n + 1 balanced sequence x , such thatf (x) = y . If the function can be calculated for linear time, then the point is in the hat.
We generate a bracketed balanced sequence x according to the uniform distribution and return f (x).
All the tricks in the function. If you want, you can stop and try to come up with one yourself. It doesn’t work, it's okay. Now I will get a rabbit out of the mathematics world from the cylinder, and everyone will be fine.
Suppose we have a counter, and initially it is zero. Let's go over the sequence. For each opening bracket we will add a point, for each closing bracket - subtract.
balance = 0
for c in seq:
balance += 1 if c == '(' else -1
The graph below shows how the counter changes
balanceas you move along the sequence. 
Sequences painted in separate colors are called indecomposable. Those. in general, a sequence is indecomposable if the counter on it assumes a zero value only at the start and end points. You can see that indecomposable sequences fall into two categories: those that are entirely above the zero level, and those that are lower. The former will be called positive sequences, the latter negative.
We calculate the total length of the negative subsequences and divide it in half. The obtained value is called a sequence defect. The correct sequences have zero defect. If we replace all the brackets in the correct sequence of length 2 non the contrary, the defect will be n .
Attention, rabbit! Chang-Feller Theorem. The number of bracket sequences of length 2 n with defect k is equal to the n- th number of Catalan
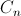 and does not depend on k .
and does not depend on k . The theorem is interesting in that it divides all balanced sequences of length 2 n into n + 1 classes of the same size, and among the classes there is a separate class containing all the correct bracket sequences. Therefore, we can try to come up with a function that encodes every sequence x with defect k with the correct sequence y, and from the sequence y and the defect k, we could uniquely reconstruct x .
If we manage to come up with such a function, then we get that for every correct sequence there are exactly n + 1 balanced with defects from 0 to n . It seems to be easy.
Attempt 1.
Let's take all the negative subsequences and invert, i.e. replace the brackets with the opposite.

Plus such a function, it retains the position of all indecomposable sequences. Minus - we lose all information about which subsequence was negative and which was positive. Even knowing that the defect was 3, we cannot restore the initial sequence from the example.
Attempt 2.
Let's invert all negative subsequences, and then put them to the end.

Now, knowing the defect, we can recover the negative subsequences. But we lost the position where they were.
Attempt 3.
We take an arbitrary indecomposable negative sequence and tear off its extreme brackets, and invert the result.
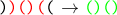
Such an operation is called cunning inversion and denoted by g . Since the sequence is indecomposable and negative, the result will always be the correct bracket sequence. The trick of the function g is that, on the one hand, it is reversible, and on the other, we have two extra brackets that can be used to encode the position of a negative subsequence.
We finish Attempt 2, only now we take out the negative sequences in the reverse order and artfully invert them through the g function :
![\ texttt {() {\ color {red})) ((} (()) {\ color {red}) (}} \ rightarrow \ texttt {() {\ color {blue} \ bf [} (() ) {\ color {blue} \ bf [} {\ color {blue} \ bf]} {\ color {green} e}} _ {\ texttt {\ color {red}) (}} \ texttt {{\ color {blue} \ bf]} {\ color {green} ()}} _ \ texttt {\ color {red})) ((}](https://habrastorage.org/getpro/habr/post_images/e07/77b/0aa/e0777b0aa19cbdad72a0f21933700520.gif)
As you can see from the example, the position of the negative subsequence can be noted by the free brackets. I highlighted them in blue and made them square. The letter e means an empty sequence.
Find out which brackets are green and which blue can be defective, which means that you can restore the initial sequence itself. This is what you need!
Atkinson and Sack proposed a recursive formula for the function f:
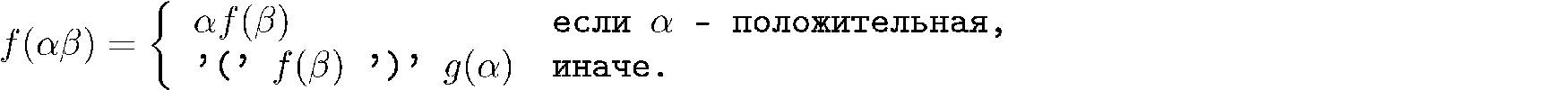
Here is an
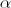 indecomposable subsequence, and
indecomposable subsequence, and 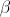 is the remainder.
is the remainder. Below I am attaching an implementation of the algorithm in Python with expanded recursion. It is easy to understand that the algorithm runs linear time.
def tryAndFix(n):
seq = ['(', ')'] * n
random.shuffle(seq)
stack = []
result = []
balance = 0
prev = 0
for pos in range( len(seq) ):
balance += 1 if seq[pos] == '(' else -1
if balance == 0:
if seq[prev] == '(':
result.extend( seq[ prev : pos + 1 ] )
else:
result.append('(')
stack.append( [ ')' if v == '(' else '(' for v in seq[ prev + 1 : pos ] ] )
prev = pos + 1
for lst in reversed(stack):
result.append(')')
result.extend(lst)
return result
Tree generation
If you read to this place, I am very happy. All that remains is to convert the sequence to a tree.
Bracket sequences of length 2 n perfectly encode trees of arbitrary arity with n + 1 vertices. Indeed, let's start a search in depth. At the entrance to the vertex, we write the opening bracket, at the exit - the closing bracket.
At the same time, trees of arbitrary arity from n + 1 can be put in one-to-one correspondence with binary trees from n vertices. All that is needed is to first write down trees of arbitrary arity in the form “left child - right neighbor”, and then rename the right neighbor to the right child.

Thank you for being with us!
References
- “Uniform Random Generation of Balanced Parenthesis Strings” DB Arnold, MR Sleep, 1980 - the first article on the generation of random bracket sequences.
- "Generating binary trees at random" MD Atkinson, J.-R. Sack, 1992
- Script on Pastbin
