The Neural Network in Practice: The Traveling Salesman Problem
Good afternoon, dear hub users.
I would like to share the practical application of one of the neurodynamic algorithms, in the continuation of my post Modeling the neural network Boltzmann Machine .
Implementation on the example of solving the traveling salesman problem.
Let me remind you a little of what its essence is.

The task of the traveling salesman (traveling salesman (French commis voyageur, outdated) is a traveling sales intermediary) is to find the most profitable route passing through these cities. Under the conditions of the problem, the route’s profitability criterion (the shortest, cheapest, aggregate criterion, etc.) and the corresponding distance, cost, etc. matrices are indicated. As a rule, it is indicated that the route should go through each city only once - in this case, the choice is made among the Hamiltonian cycles.
To solve this problem, a network consisting of 100 neurons is used.
When assigning weights, there must be a guarantee that the neural network provides a solution that matches the correct tour. It becomes clear why the assignment of weights is most significant for achieving a good solution when using the Boltzmann machine and the Hopfield network. Hopfield and Tank proposed one way to assign weights for Boltzmann machines. The main idea is to impose fines on incorrect tours and at the same time minimize the length of the tour. The Aarts approach makes it possible to formally establish assignments, relating to the task, while many other approaches for assigning weights are heuristic. Of course, it is not necessarily implied that the resulting algorithm works well, so Aarts offers several modifications designed to improve the performance of large tasks.
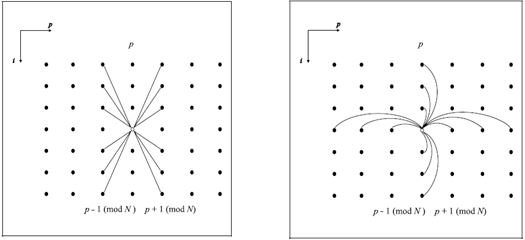
Fig. 14 Fig. 15
Figures (14) and (15) illustrate the connections made to each network node. They are divided into two types. Compounds of distances for which weights are chosen so that if the network is in a state that corresponds to the tour, these weights will reflect the cost of the energy of the connection (p-1) of the tour city with p city, and p - the city with the city (p + 1).
Figure (14) shows distance compounds. Each node (i, p) has inhibitory connections to two adjacent columns, whose weights reflect the cost of connecting the three cities.
Figure (15) shows the exclusive connections. Each node (i, p) has inhibitory connections to all elements in the same row and column.
Exclusive compounds prohibit two elements from being in the same row or column at the same time. Exclusive connections allows the network to establish itself in a state corresponding to the state of the tour.
Since all connections are still forbidding, we must provide the network with some incentive to include elements by manipulating thresholds. Intuitively, we can see that some arrangements, such as those shown in figures (14) and (15), may have the desired effect, but the following theorem shows how to choose weights accurately. Consider the following set of parameters: (13) Where, dij is the distance between i and j cities, N is the number of cities, eipjq is the energy between the neurons (j, q) and (i, p).
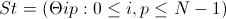
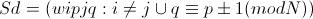
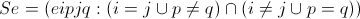
Note that each element in figures (14) and (15) is in the table; therefore, any particular element is identified by two signatures. θip is the input of the element (i, p), and wipjq is the weight from the element (j, q) to (i, p).
We choose weights and inputs in such a way that (14) Then 1. Feasibility. The correct states of the network tours exactly correlate with the local minimum of energy 2. Ordering. The energy function is order-saving according to the length of the tour.
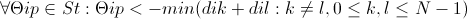
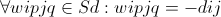
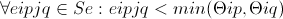
The proof is fairly straightforward and depends on the demonstration that the states of the tours are exactly correlated with the local minimum of energy. In an asynchronous Boltzmann machine, local energy minima correspond exactly to fixed points. The disadvantage of the algorithm is that in the synchronous case, some local energy minima can also correspond to two cycles, which complicates the assignment of weights in the synchronous case.
When solving the traveling salesman problem, the functioning of the network is as follows:
1. The scales are calculated, taking into account the task at hand, according to the algorithm described above.
2. A signal is supplied to the input
3. Neurons are activated according to the Boltzmann training algorithm, except that the weights are always the same.
4. Actions 2 and 3 are repeated until the energy falls into the global minimum (that is, during n calculations it does not change its state).
Algorithm Optimization
Solving the problem using the “Annealing Simulation” algorithm, in addition to the correct selection of weights, input vector, threshold values, and dimension, the parameter t (temperature) is no less important.
The metal is annealed, heating it to a temperature exceeding its melting point, and then letting it cool slowly. At high temperatures, atoms, possessing high energies and freedom of movement, randomly accept all possible configurations. With a gradual decrease in temperature, the atomic energies decrease, and the system as a whole tends to adopt a configuration with minimal energy. When cooling is complete, a state of global minimum energy is reached.
At a fixed temperature, the energy distribution of the system is determined by the Boltzmann probability factor.
This is obvious: there is a finite probability that the system has high energy even at low temperatures. Similarly, there is a small but calculated probability that a kettle of water on a fire freezes before it boils.
The statistical distribution of energies allows the system to exit from local energy minima. At the same time, the probability of high-energy states decreases rapidly with decreasing temperature. Therefore, at low temperatures, there is a strong tendency to occupy a low-energy state.
For a more flexible temperature change, the entire graph was divided into intervals in which the user himself can change the rate of temperature drop (up to 50 iterations, from 50 to 120 iterations, more than 120 iterations).
In the process of practical research, the following regularities were deduced:
1. At high temperatures, the energy behaves randomly, when at low temperatures it becomes almost deterministic.
2. Changing the temperature to any constant in any interval, most often the algorithm finds a path between all cities, but at least far from optimal.
3. To obtain the most accurate answer, it is necessary at low temperatures to significantly reduce the rate of fall of the parameter t, which cannot be said about high temperatures. When the temperature is maximum, the drop rate has almost no effect on the result.
In the process of these studies, we found that temperature is much more important than any other parameter involved in the calculations to achieve the most accurate result (in this case, the smallest path between cities). This can be achieved by reducing the rate of fall of the parameter t at the final stage of the calculations. In the network model we use, it is recommended to reduce the interval “after 120 iterations”.
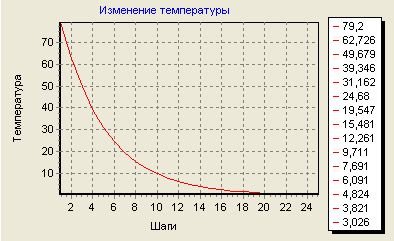
For a visual representation of the results obtained in the program developed by us, simulating the network, a temperature graph is provided at which the optimal result was achieved.
Studies have also been carried out in the field of neural network activation. In addition to the standard change in the state of each neuron individually selected at random, activation is carried out by a group of neurons (in this model, the group includes 10 neurons). Each neuron in this group changes its state to the opposite. This activation method allows you to parallelize the calculation process even more, which leads to faster finding the right solution. The number of calculation steps was reduced from 534 to 328.
Thus, it is possible to optimize a given neural network not only for accuracy by changing the temperature graph, but also the speed of finding the correct answer by increasing the number of neurons that change their state at one time.
I would like to share the practical application of one of the neurodynamic algorithms, in the continuation of my post Modeling the neural network Boltzmann Machine .
Implementation on the example of solving the traveling salesman problem.
Let me remind you a little of what its essence is.

The task of the traveling salesman (traveling salesman (French commis voyageur, outdated) is a traveling sales intermediary) is to find the most profitable route passing through these cities. Under the conditions of the problem, the route’s profitability criterion (the shortest, cheapest, aggregate criterion, etc.) and the corresponding distance, cost, etc. matrices are indicated. As a rule, it is indicated that the route should go through each city only once - in this case, the choice is made among the Hamiltonian cycles.
To solve this problem, a network consisting of 100 neurons is used.
When assigning weights, there must be a guarantee that the neural network provides a solution that matches the correct tour. It becomes clear why the assignment of weights is most significant for achieving a good solution when using the Boltzmann machine and the Hopfield network. Hopfield and Tank proposed one way to assign weights for Boltzmann machines. The main idea is to impose fines on incorrect tours and at the same time minimize the length of the tour. The Aarts approach makes it possible to formally establish assignments, relating to the task, while many other approaches for assigning weights are heuristic. Of course, it is not necessarily implied that the resulting algorithm works well, so Aarts offers several modifications designed to improve the performance of large tasks.

Fig. 14 Fig. 15
Figures (14) and (15) illustrate the connections made to each network node. They are divided into two types. Compounds of distances for which weights are chosen so that if the network is in a state that corresponds to the tour, these weights will reflect the cost of the energy of the connection (p-1) of the tour city with p city, and p - the city with the city (p + 1).
Figure (14) shows distance compounds. Each node (i, p) has inhibitory connections to two adjacent columns, whose weights reflect the cost of connecting the three cities.
Figure (15) shows the exclusive connections. Each node (i, p) has inhibitory connections to all elements in the same row and column.
Exclusive compounds prohibit two elements from being in the same row or column at the same time. Exclusive connections allows the network to establish itself in a state corresponding to the state of the tour.
Since all connections are still forbidding, we must provide the network with some incentive to include elements by manipulating thresholds. Intuitively, we can see that some arrangements, such as those shown in figures (14) and (15), may have the desired effect, but the following theorem shows how to choose weights accurately. Consider the following set of parameters: (13) Where, dij is the distance between i and j cities, N is the number of cities, eipjq is the energy between the neurons (j, q) and (i, p).
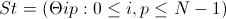
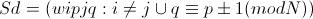
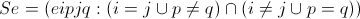
Note that each element in figures (14) and (15) is in the table; therefore, any particular element is identified by two signatures. θip is the input of the element (i, p), and wipjq is the weight from the element (j, q) to (i, p).
We choose weights and inputs in such a way that (14) Then 1. Feasibility. The correct states of the network tours exactly correlate with the local minimum of energy 2. Ordering. The energy function is order-saving according to the length of the tour.
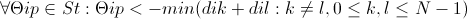
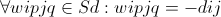
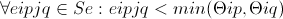
The proof is fairly straightforward and depends on the demonstration that the states of the tours are exactly correlated with the local minimum of energy. In an asynchronous Boltzmann machine, local energy minima correspond exactly to fixed points. The disadvantage of the algorithm is that in the synchronous case, some local energy minima can also correspond to two cycles, which complicates the assignment of weights in the synchronous case.
When solving the traveling salesman problem, the functioning of the network is as follows:
1. The scales are calculated, taking into account the task at hand, according to the algorithm described above.
2. A signal is supplied to the input
3. Neurons are activated according to the Boltzmann training algorithm, except that the weights are always the same.
4. Actions 2 and 3 are repeated until the energy falls into the global minimum (that is, during n calculations it does not change its state).
Algorithm Optimization
Solving the problem using the “Annealing Simulation” algorithm, in addition to the correct selection of weights, input vector, threshold values, and dimension, the parameter t (temperature) is no less important.
The metal is annealed, heating it to a temperature exceeding its melting point, and then letting it cool slowly. At high temperatures, atoms, possessing high energies and freedom of movement, randomly accept all possible configurations. With a gradual decrease in temperature, the atomic energies decrease, and the system as a whole tends to adopt a configuration with minimal energy. When cooling is complete, a state of global minimum energy is reached.
At a fixed temperature, the energy distribution of the system is determined by the Boltzmann probability factor.
This is obvious: there is a finite probability that the system has high energy even at low temperatures. Similarly, there is a small but calculated probability that a kettle of water on a fire freezes before it boils.
The statistical distribution of energies allows the system to exit from local energy minima. At the same time, the probability of high-energy states decreases rapidly with decreasing temperature. Therefore, at low temperatures, there is a strong tendency to occupy a low-energy state.
For a more flexible temperature change, the entire graph was divided into intervals in which the user himself can change the rate of temperature drop (up to 50 iterations, from 50 to 120 iterations, more than 120 iterations).
In the process of practical research, the following regularities were deduced:
1. At high temperatures, the energy behaves randomly, when at low temperatures it becomes almost deterministic.
2. Changing the temperature to any constant in any interval, most often the algorithm finds a path between all cities, but at least far from optimal.
3. To obtain the most accurate answer, it is necessary at low temperatures to significantly reduce the rate of fall of the parameter t, which cannot be said about high temperatures. When the temperature is maximum, the drop rate has almost no effect on the result.
In the process of these studies, we found that temperature is much more important than any other parameter involved in the calculations to achieve the most accurate result (in this case, the smallest path between cities). This can be achieved by reducing the rate of fall of the parameter t at the final stage of the calculations. In the network model we use, it is recommended to reduce the interval “after 120 iterations”.
For a visual representation of the results obtained in the program developed by us, simulating the network, a temperature graph is provided at which the optimal result was achieved.

Studies have also been carried out in the field of neural network activation. In addition to the standard change in the state of each neuron individually selected at random, activation is carried out by a group of neurons (in this model, the group includes 10 neurons). Each neuron in this group changes its state to the opposite. This activation method allows you to parallelize the calculation process even more, which leads to faster finding the right solution. The number of calculation steps was reduced from 534 to 328.
Thus, it is possible to optimize a given neural network not only for accuracy by changing the temperature graph, but also the speed of finding the correct answer by increasing the number of neurons that change their state at one time.
