Hidden Markov chains, Viterbi algorithm
We need to implement a lie detector, which, by trembling a person’s hands, determines whether he is telling the truth or not. Suppose when a person is lying, his hands are shaking a little more. The signal may be:
An interesting method is described in the article “A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition” by LR Rabiner, which introduces the Markov hidden chain model and describes three valuable algorithms: The Forward-Backward Procedure , Viterbi Algorithm and Baum -Welch reestimation . Despite the fact that these algorithms are of interest only in aggregate, for a better understanding, it is better to describe them separately.
The hidden Markov chain method is widely used, for example, it is used to search for CG islands(DNA, RNA sites with a high density of a bunch of cytosine and guanine), while Lawrence Rabiner himself used it for speech recognition. The algorithms came in handy for me in order to track the change in the stages of sleep / wake according to the electroencephalogram and look for epileptic seizures.
In the model of hidden Markov chains, it is assumed that the system in question has the following properties:
The HMM model can be described as: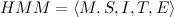
Time t is assumed to be discrete, given by non-negative integers, where 0 corresponds to the initial moment of time, and Tm to the largest value.
When we have 2 hidden states, and the observed values obey the normal distribution with different variances, as in the example with the lie detector, for each of the states the algorithm of the system’s functioning can be represented as follows:

A simpler description was already mentioned in Probabilistic models: examples and pictures .
The choice of the distribution vector of the observed values often lies with the researcher. Ideally, the observed quantity is a latent state, and the task of determining these states in this case becomes trivial. In reality, everything is more complicated, for example, the classical model described by Rabiner suggests that - finite discrete distribution. Something like the one in the graph below:
- finite discrete distribution. Something like the one in the graph below:

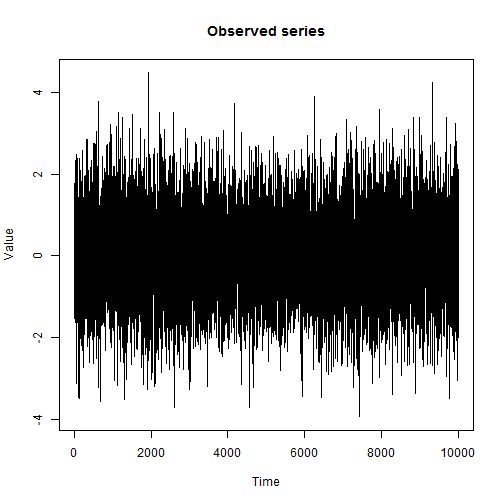
The researcher usually has the freedom to choose the distribution of the observed states. The stronger the observed values distinguish hidden states, the better. From a programming point of view, enumerating various observable characteristics means the need for careful encapsulation . The graph below shows an example of the initial data for the lie detector problem, where the distribution of the observed characteristic (hand shake) is continuous, since it was modeled as normal with an average of 0 for both states, with a dispersion of 1 when the person is telling the truth (purple columns) and 1.21 when lying (green columns):
. The graph below shows an example of the initial data for the lie detector problem, where the distribution of the observed characteristic (hand shake) is continuous, since it was modeled as normal with an average of 0 for both states, with a dispersion of 1 when the person is telling the truth (purple columns) and 1.21 when lying (green columns):

In order not to touch upon the issues of setting up the model, we consider a simplified task.
Given:
two hidden states, where fair behavior corresponds to white noise with a dispersion of 1, lies - white noise with a dispersion of 1.21;
sample of 10,000 consecutive observations o;
change of state occurs on average once every 2,500 cycles.
It is required to determine the moments of state transition.
Solution:
Let's set the five parameters of the model:
We will find the most plausible states for each moment in time using the Viterbi algorithm for given model parameters.
The solution of the problem is reduced to specifying the model and running the Viterbi algorithm.
According to the model of hidden Markov chains and the sample of values of the observed characteristics, we find a sequence of states that would best describe the sample in a given model. The concept can best be interpreted in different ways, but a well-established solution is the Viterbi algorithm, which finds such a sequence that
that 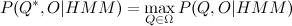 .
.
The search problem is solved using dynamic programming, for this we consider the function:
solved using dynamic programming, for this we consider the function:
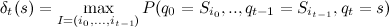
where Is the greatest probability of being in state s at time t. Recursively, this function can be defined as follows:
Is the greatest probability of being in state s at time t. Recursively, this function can be defined as follows:

Simultaneously with the calculation for each moment in time, we remember the most probable state from which we arrived, that is
for each moment in time, we remember the most probable state from which we arrived, that is 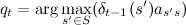 , at which the maximum was reached. At the same time
, at which the maximum was reached. At the same time  , it means that you can recover
, it means that you can recover  by going through them in the reverse order. You may notice that
by going through them in the reverse order. You may notice that  is the value of the desired probability. Required sequence
is the value of the desired probability. Required sequence  found. An interesting property of the algorithm is that the estimated function of the observed characteristics is included in
found. An interesting property of the algorithm is that the estimated function of the observed characteristics is included in  the form of a factor. If we assume that
the form of a factor. If we assume that 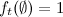 , then in the case of gaps in the observations, you can still evaluate the most likely hidden states at these moments.
, then in the case of gaps in the observations, you can still evaluate the most likely hidden states at these moments.
The pseudo-code for Viterbi's algorithm is outlined below. It should be noted that all operations with vectors and matrices are element-wise .
Someone could recognize the R code in this “pseudo-code” , but this is far from the best implementation.
Let us compare the periods of constancy of the states that were set during the simulation (upper part of the graph) and those that were found using the Viterbi algorithm (lower part of the graph):
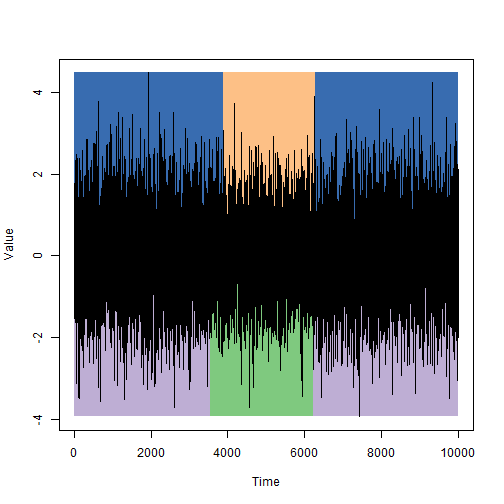
It is quite worthy in my opinion, but you should not rely on this every time.
The Viterbi algorithm described earlier requires the definition of a hidden Markov chain model (Arguments of the viterbi function). For their task, a simple initialization is used, which implies that in addition to the selection of the observed values of O, the corresponding selection of the hidden states Q, which are known to us from somewhere, is also given. In this case, the formulas for evaluating the parameters will look like this:
![S \ leftarrow \ left \ {s: q_t = s, t \ in [0, T_m] \ right \} \\ M \ leftarrow \ | S \ | \\ I \ leftarrow \ left (\ frac {\ sum_ {t \ in [0, T_m]} Id (q_t = s)} {T_m + 1}, s \ in S \ right) \\ T \ leftarrow \ left (\ frac {\ sum_ {t \ in [1, T_m]} Id (q_ {t-1} = s', q_t = s)} {\ sum_ {t \ in [0, T_m]} (\ sum_ { t \ in [1, T_m]} Id (q_ {t-1} = s ')}, s, s' \ in S \ right) \\ E \ leftarrow \ left (f_s (o_t) = \ frac {\ sum_ {t \ in [0, T_m]} Id (q_t = s, o_t = e)} {\ sum_ {t \ in [0, T_m]} Id (q_t = s)}, s \ in S \ right)](http://mathurl.com/ark5aup.png)
where Id (x) is the indicator function.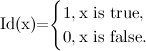
For the considered lie detector example, the algorithm incorrectly classified 413 out of 10,000 states (~ 4%), which is not bad at all. The Viterbi algorithm is capable of detecting with good accuracy the moments of a change in latent states, but only if the distributions of the observed characteristics are precisely known. If only the parametric class of such distributions is known, then there is a way to select the most suitable parameters, called the Baum-Welsh algorithm.
If interested, ask for more ...

An interesting method is described in the article “A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition” by LR Rabiner, which introduces the Markov hidden chain model and describes three valuable algorithms: The Forward-Backward Procedure , Viterbi Algorithm and Baum -Welch reestimation . Despite the fact that these algorithms are of interest only in aggregate, for a better understanding, it is better to describe them separately.
The hidden Markov chain method is widely used, for example, it is used to search for CG islands(DNA, RNA sites with a high density of a bunch of cytosine and guanine), while Lawrence Rabiner himself used it for speech recognition. The algorithms came in handy for me in order to track the change in the stages of sleep / wake according to the electroencephalogram and look for epileptic seizures.
In the model of hidden Markov chains, it is assumed that the system in question has the following properties:
- at each time period, the system can be in one of a finite set of states;
- the system accidentally switches from one state to another (possibly the same) and the probability of transition depends only on the state in which it was;
- at each moment of time, the system gives one value of the observed characteristic - a random value that depends only on the current state of the system.
The HMM model can be described as:
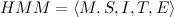
- M is the number of states;
 - a finite set of conditions;
- a finite set of conditions; Is the vector of probabilities that the system is in state i at time 0;
Is the vector of probabilities that the system is in state i at time 0;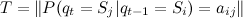 - matrix of probabilities of transition from state i to state j for
- matrix of probabilities of transition from state i to state j for ![\ forall t \ in [1, T_m]](https://habrastorage.org/getpro/habr/post_images/f35/bc4/b80/f35bc4b80fe1243b2277ae615cd731cb.png) ;
; ,
, 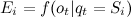 Is the vector of distributions of observable random variables corresponding to each of the states defined as functions of density or distribution defined on O (the set of observable values for all states).
Is the vector of distributions of observable random variables corresponding to each of the states defined as functions of density or distribution defined on O (the set of observable values for all states).
Time t is assumed to be discrete, given by non-negative integers, where 0 corresponds to the initial moment of time, and Tm to the largest value.
When we have 2 hidden states, and the observed values obey the normal distribution with different variances, as in the example with the lie detector, for each of the states the algorithm of the system’s functioning can be represented as follows:

A simpler description was already mentioned in Probabilistic models: examples and pictures .
The choice of the distribution vector of the observed values often lies with the researcher. Ideally, the observed quantity is a latent state, and the task of determining these states in this case becomes trivial. In reality, everything is more complicated, for example, the classical model described by Rabiner suggests that
 - finite discrete distribution. Something like the one in the graph below:
- finite discrete distribution. Something like the one in the graph below: 
The researcher usually has the freedom to choose the distribution of the observed states. The stronger the observed values distinguish hidden states, the better. From a programming point of view, enumerating various observable characteristics means the need for careful encapsulation
 . The graph below shows an example of the initial data for the lie detector problem, where the distribution of the observed characteristic (hand shake) is continuous, since it was modeled as normal with an average of 0 for both states, with a dispersion of 1 when the person is telling the truth (purple columns) and 1.21 when lying (green columns):
. The graph below shows an example of the initial data for the lie detector problem, where the distribution of the observed characteristic (hand shake) is continuous, since it was modeled as normal with an average of 0 for both states, with a dispersion of 1 when the person is telling the truth (purple columns) and 1.21 when lying (green columns): 
In order not to touch upon the issues of setting up the model, we consider a simplified task.
Given:
two hidden states, where fair behavior corresponds to white noise with a dispersion of 1, lies - white noise with a dispersion of 1.21;
sample of 10,000 consecutive observations o;
change of state occurs on average once every 2,500 cycles.
It is required to determine the moments of state transition.
Solution:
Let's set the five parameters of the model:
- the number of states M = 2;
- S = {1,2};
- experience shows that the initial distribution is practically irrelevant, therefore I = (0.5,0.5);
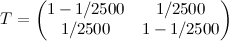 ;
;- E = (N (0,1), N (0,1.21)).
We will find the most plausible states for each moment in time using the Viterbi algorithm for given model parameters.
The solution of the problem is reduced to specifying the model and running the Viterbi algorithm.
According to the model of hidden Markov chains and the sample of values of the observed characteristics, we find a sequence of states that would best describe the sample in a given model. The concept can best be interpreted in different ways, but a well-established solution is the Viterbi algorithm, which finds such a sequence
 that
that 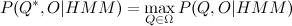 .
. The search problem is
 solved using dynamic programming, for this we consider the function:
solved using dynamic programming, for this we consider the function: 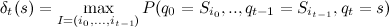
where
 Is the greatest probability of being in state s at time t. Recursively, this function can be defined as follows:
Is the greatest probability of being in state s at time t. Recursively, this function can be defined as follows: 
Simultaneously with the calculation
 for each moment in time, we remember the most probable state from which we arrived, that is
for each moment in time, we remember the most probable state from which we arrived, that is 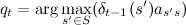 , at which the maximum was reached. At the same time
, at which the maximum was reached. At the same time  , it means that you can recover
, it means that you can recover  by going through them in the reverse order. You may notice that
by going through them in the reverse order. You may notice that  is the value of the desired probability. Required sequence
is the value of the desired probability. Required sequence  found. An interesting property of the algorithm is that the estimated function of the observed characteristics is included in
found. An interesting property of the algorithm is that the estimated function of the observed characteristics is included in  the form of a factor. If we assume that
the form of a factor. If we assume that 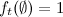 , then in the case of gaps in the observations, you can still evaluate the most likely hidden states at these moments.
, then in the case of gaps in the observations, you can still evaluate the most likely hidden states at these moments.The pseudo-code for Viterbi's algorithm is outlined below. It should be noted that all operations with vectors and matrices are element-wise .
Tm<-10000 # Max time
M<-2 # Number of states
S<-seq(from=1, to=M) # States [1,2]
I<-rep(1./M, each=M) # Initial distribution [0.5, 0.5]
T<-matrix(c(1-4./Tm, 4./Tm, 4./Tm,1-4./Tm),2) #[0.9995 0.0005; 0.0005 0.9995]
P<-c(function(o){dnorm(o)}, function(o){dnorm(o,sd=1.1)}) # Vector of density functions for each state (N(0,1), N(0,1.21))
E<-function(P,s,o){P[[s]](o)} # Calculate probability of observed value o for state s.
Es<-function(E,P,o) {
# Same for all states
probs<-c()
for(s in S) {
probs<-append(probs, E(P,s,o))
}
return(probs)
}
viterbi<-function(S,I,T,P,E,O,tm) {
delta<-I*Es(E,P,O[1]) # initialization for t=1
prev_states<-cbind(rep(0,length(S))) # zeros
for(t in 2:Tm) {
m<-matrix(rep(delta,length(S)),length(S))*T # delta(s')*T[ss'] forall s,s'
md<-apply(m,2,max) # search for max delta(s) by s' for all s
max_delta<-apply(m,2,which.max)
prev_states<-cbind(prev_states,max_delta)
delta<-md*Es(E,P,O[t]) # prepare next step delta(s)
}
return(list(delta=delta,ps=prev_states)) # return delta_Tm(s) and paths
}
restoreStates<-function(d,prev_states) {
idx<-which.max(d)
s<-c(idx)
sz<-length(prev_states[1,])
for(i in sz:2) {
idx<-prev_states[idx,i]
s<-append(s,idx,after=0)
}
return (as.vector(s))
}
Someone could recognize the R code in this “pseudo-code” , but this is far from the best implementation.
Let us compare the periods of constancy of the states that were set during the simulation (upper part of the graph) and those that were found using the Viterbi algorithm (lower part of the graph):

It is quite worthy in my opinion, but you should not rely on this every time.
The Viterbi algorithm described earlier requires the definition of a hidden Markov chain model (Arguments of the viterbi function). For their task, a simple initialization is used, which implies that in addition to the selection of the observed values of O, the corresponding selection of the hidden states Q, which are known to us from somewhere, is also given. In this case, the formulas for evaluating the parameters will look like this:
![S \ leftarrow \ left \ {s: q_t = s, t \ in [0, T_m] \ right \} \\ M \ leftarrow \ | S \ | \\ I \ leftarrow \ left (\ frac {\ sum_ {t \ in [0, T_m]} Id (q_t = s)} {T_m + 1}, s \ in S \ right) \\ T \ leftarrow \ left (\ frac {\ sum_ {t \ in [1, T_m]} Id (q_ {t-1} = s', q_t = s)} {\ sum_ {t \ in [0, T_m]} (\ sum_ { t \ in [1, T_m]} Id (q_ {t-1} = s ')}, s, s' \ in S \ right) \\ E \ leftarrow \ left (f_s (o_t) = \ frac {\ sum_ {t \ in [0, T_m]} Id (q_t = s, o_t = e)} {\ sum_ {t \ in [0, T_m]} Id (q_t = s)}, s \ in S \ right)](http://mathurl.com/ark5aup.png)
where Id (x) is the indicator function.
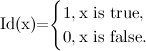
For the considered lie detector example, the algorithm incorrectly classified 413 out of 10,000 states (~ 4%), which is not bad at all. The Viterbi algorithm is capable of detecting with good accuracy the moments of a change in latent states, but only if the distributions of the observed characteristics are precisely known. If only the parametric class of such distributions is known, then there is a way to select the most suitable parameters, called the Baum-Welsh algorithm.
If interested, ask for more ...
