Regularization in a restricted Boltzmann machine, experiment

Hey. In this post, we will conduct an experiment in which we test two types of regularization in a restricted Boltzmann machine . As it turned out, RBM is very sensitive to model parameters, such as moment and local field of a neuron (for more details on all parameters, see Jeffrey Hinton’s practical guide in RBM ). But for a complete picture and for getting patterns like these , one more parameter was missing - regularization. Limited Boltzmann machines can be treated both as a kind of Markov network, and as another neural network, but if you dig deeper, you will see an analogy with vision. Like the primary visual cortexreceiving information from the retina through the optic nerve (may biologists forgive me for such a simplification), RBM is looking for simple patterns in the input image. The analogy does not end there, if very small and zero weights are interpreted as lack of weight, then we get that each hidden RBM neuron forms a receptive field , and the deep network formed from trained RBMs forms more complex features from simple images; In principle, the visual cortex of the brain is engaged in something similar, though, probably, it’s more complicated =)

L1 and L2 regularization

We will begin, perhaps, with a brief description of what a regularization of a model is — a way to impose a penalty on the objective function for the complexity of the model. From a Bayesian point of view, this is a way to take into account some a priori information about the distribution of model parameters. An important property is that regularization helps to avoid retraining the model. We denote the model parameters as θ = {θ_i}, i = 1..n. The final objective function C = η (E + λR) , where E is the main objective function of the model, R = R (θ) is the function of the model parameters, this and lambdaIs the learning speed and the regularization parameter, respectively. Thus, to calculate the gradient of the final objective function, it will be necessary to calculate the gradient of the regularization function:



We consider two types of regularization whose roots are in the Lp metric . The regularization function L1 and its derivatives are as follows:





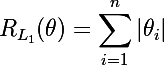
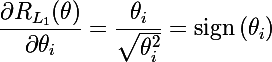
L2 regularization is as follows:





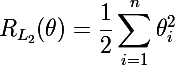
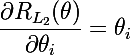
Both regularization methods fine the model for a large value of the weight, in the first case the absolute value of the weight, in the second the square of the weight, so the distribution of the weights will approach normal with the center at zero and a large peak. A more detailed comparison of L1 and L2 can be found here . As we will see later, about 70% of the weights will be less than 10 ^ (- 8).

Regularization in RBM

In a post the year before, I described an example of RBM implementation in C # . I will rely on the same implementation in order to show where the regularization is embedded, but first the formulas. The goal of RBM training is to maximize the likelihood that the reconstructed image will be identical to the input:



In general, the probability logarithm is maximized in the algorithm, and to introduce a penalty, it is necessary to subtract the value of the regularization function from the obtained probability, as a result, the new objective function takes the following form: The



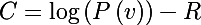
derivative of such a function the parameter will look like this:



The contrastive divergence algorithm consists of a positive phase and a negative one, so in order to add regularization, it is enough to subtract the value of the derivative of the regularization function from the value of the positive phase, after subtracting the negative phase:



We proceed to the experiments. As test data, the same set was used as in the year before last post . In all cases, training was conducted exactly 1000 eras. I will give two ways to visualize the patterns found, in the first case (the picture in gray tones), the dark value corresponds to the minimum weight value, and white to the maximum; in the second figure, black corresponds to zero, an increase in the red component corresponds to an increase in the positive direction, and an increase in the blue component to the negative. I will also give a histogram of the distribution of weights and small comments.

Without regularization

• error value on the training set: 0.188181367765024
• error value on the cross-validation set: 21.0910315518859

The patterns turned out to be very blurry, and difficult to analyze. The average value of the balance is shifted to the left, and the absolute value of the balance reaches 2 or more.

L2 regularization

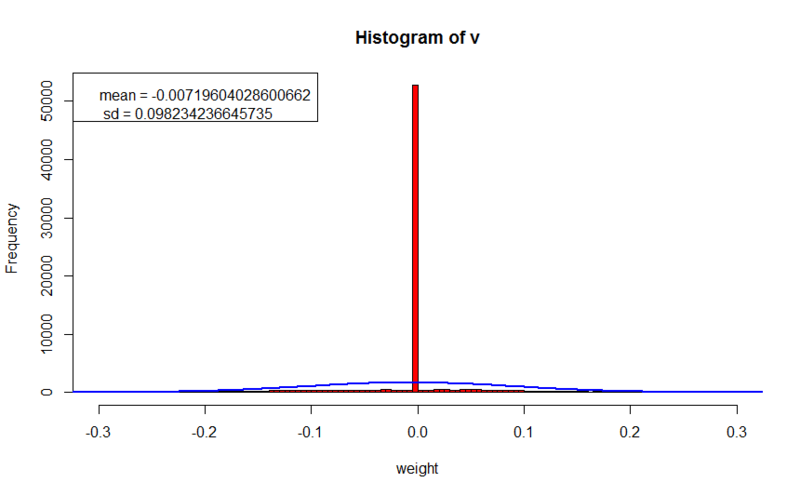
• error value on the training set: 10.1198906337165
• error value on the cross-validation set: 23.3600809429977
• regularization parameter: 0.1

Here we observe clearer images. We can already see that some characters really take into account some features of letters. Despite the fact that the error on the training set is 100 times worse than when learning without regularization, the error on the cross-validation set is not much larger than the first experiment, which suggests that the generalizing ability of the network on unfamiliar images has not deteriorated much (it is worth noting that the error calculation did not include the value of the regularization function, which allows us to compare values ​​with previous experience). The weights are concentrated around zero, and do not significantly exceed 0.2 in absolute value, which is 10 times less than in the previous experiment.

L1 regularization

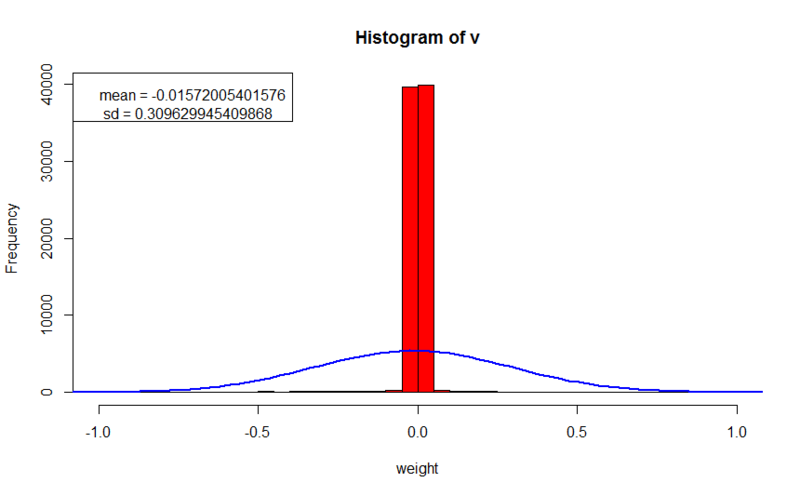
• error value on the training set: 4.42672814826447
• error value on the cross-validation set: 17.3700437102876
• regularization parameter: 0.005

In this experiment, we observe clear patterns, and especially receptive fields (around the blue-red spots, all weights are almost zero). Patterns can even be analyzed, we can notice, for example, edges from W (first row, fourth picture), or a pattern that reflects the average size of input images (in the fifth row, 8 and 10 pictures). The recovery error on the training set is 40 times worse than in the first experiment, but better than with L2 regularization, while the error on the unknown set is better than in both previous experiments, which indicates an even better generalizing ability. Weights are also concentrated around zero, and in most cases do not exceed it much. The significant difference in the regularization parameter is explained by the fact that when calculating the gradient for L2, the parameter is multiplied by the weight value, as a rule these two numbers are less than 1;

Conclusion

In conclusion, I want to say that the BSR is really a very sensitive thing to the parameters. And the main thing is not to break down in the process of finding a solution -) In the end, I will give an enlarged image of one of the RBM trained with L1 regularization, but for 5000 eras.


UPDATE :
recently trained rbm on a full set of capital letters 4 fonts 3 styles, during 5000 iterations with L1 regularization, it took about 14 hours, but the result is even more interesting, the features turned out even more local and clean